基于GSA优化模糊神经网络的静止无功补偿器的电压控制研究

谭广通

(91245部队，葫芦岛，125000)

0 引言

静止无功补偿器(Static Var Compensator，SVC)的主要作用是向电网输送或者吸收可连续调节的无功功率，提高输电系统线路的传输能力，实现电网的调压和调相作用[1]。由于基于晶闸管控制的SVC具有容量大、可靠性高、投资小、损耗低、调压效果好和补偿迅速的优点，目前被广泛地应用于电网控制系统。

由于传统的PID控制具有控制参数少，结构简单等优点，其在SVC控制中占主要地位。而SVC控制系统是一个非线性复杂的系统，因此传统的PID的稳定性和控制效率无法满足现实的需求，为克服上述缺点，将PID控制和其他算法相结合成为SVC控制研究的热点问题。

1 SVC原理

由晶闸管投切电容器(TSC)和晶闸管控制电抗器(TCR)构成的TSC+TCR组合型SVC，具有较好的输出特性和损耗特性[2]，是目前应用较为广泛的静止无功补偿装置。其典型结构如1所示。

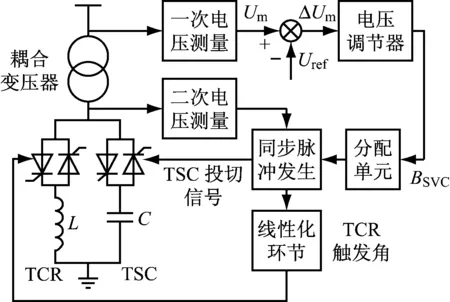
图1 SVC结构图

2 引力搜索算法

引力搜索算法(Gravitational Search Algorithm，GSA)是受万有引力定律启发而提出的一种启发式搜索算法[3]，假设一个系统有K个对象，第i个物体的位置如式(1)。

(1)

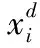
施加在第i个物体到第j个物体的力,如式(2)。

(2)

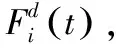
(3)

其中，randj表示位于[0 1]之间的随机数。

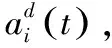
(4)

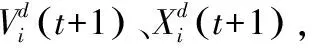
(5)

(6)

根据引力质量和惯性质量计算公式，估计引力质量和惯性质量是否相等。质量Mi(t)计算过程,如式(8)-(11)。

Mi=Mii，i=1,2,…，k,

(7)

(8)

(9)

(10)

(11)

其中，fiti(t)表示t时刻物体i适应度；best(t)、worst(t)分别表示最优适应度和最差适应度。

3 模糊PID控制

3.1 模糊控制原理

模糊控制器主要由模糊化处理、模糊推理和解模糊3个部分组成[5]。模糊PID控制框图如图2所示。

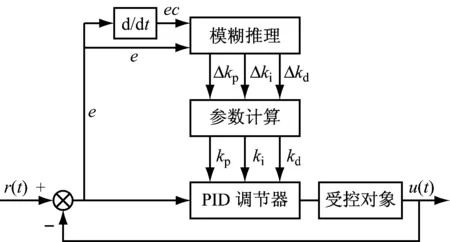
图2 模糊PID控制结构图

其中e表示误差，ec表示误差变化率，d/dt表示微分，d(e)/dt,r(t)表示给定值，u(t)表示被控量。kp,ki,kd分别表示比例系数、积分系数和微分系数。

3.2 模糊PID控制器的设计

模糊PID控制器采用二维控制器[6]，误差e和误差变化率ec作为控制器的2个输入量，二者的论域为[-6,6]，Δkp,Δki,Δkd作为控制器的3个输出量，其论域为[-3,3]。误差e、误差变化率ec以及Δkp,Δki,Δkd的模糊子集均由7个子集组成[7]，即{负大，负中，负小，零，正小，正中，正大}，对应的英文缩写为{NB,NM,NS,ZE,PS,PM,PB}。

模糊控制的控制规则根据实际经验获得[8-9]，Δkp,Δki,Δkd的模糊规则如表1-表3所示。

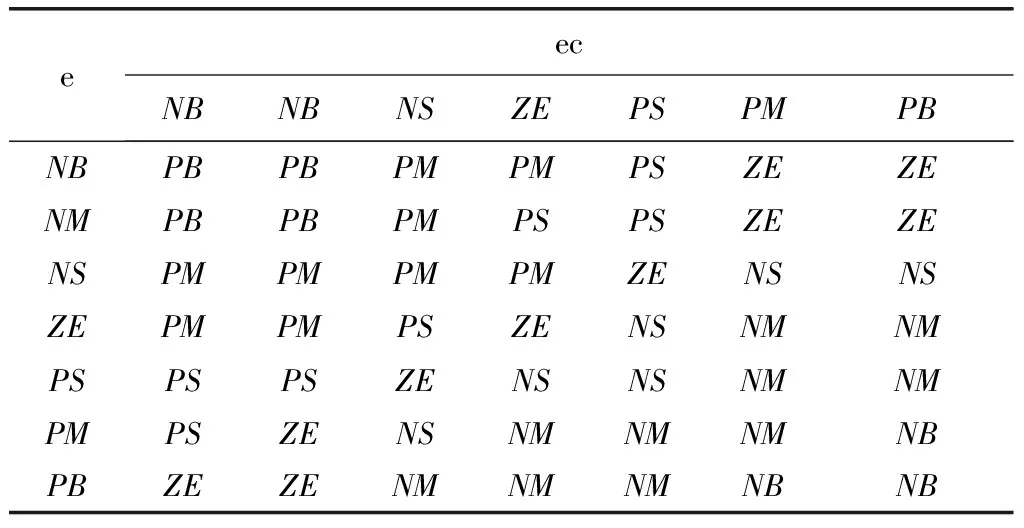
表1 Δkp的模糊规则

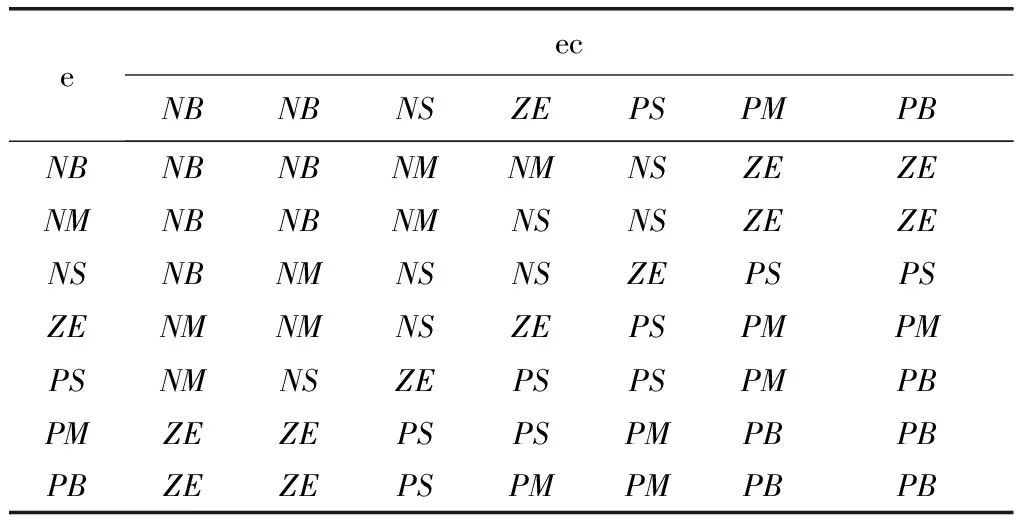
表2 Δki的模糊规则

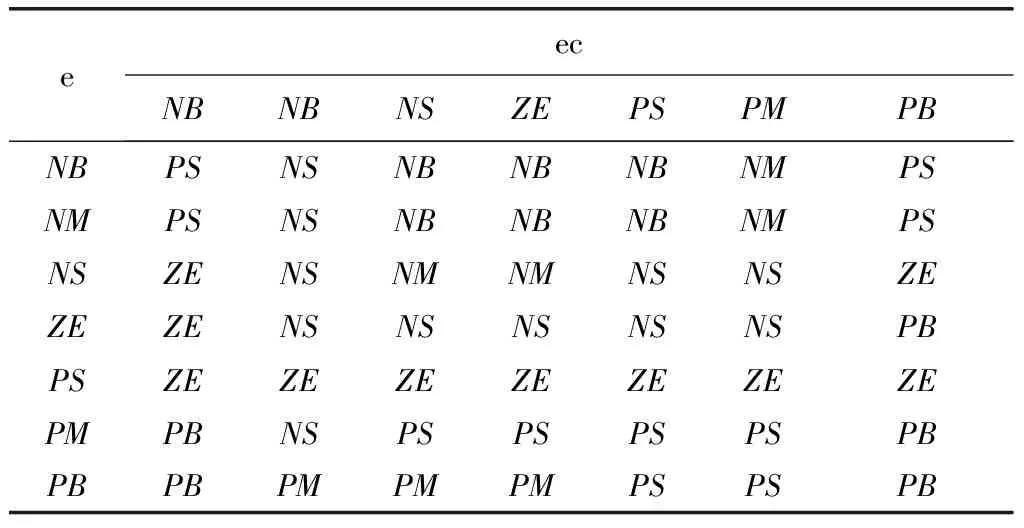
表3 Δkd的控制规则

规则如下所示。

Ifeis NB andecis NB，then Δkpis PB，Δkiis NB，Δkdis PS；

Ifeis NB andecis NM，then Δkpis PB，Δkiis NB，Δkdis NS；

……

模糊规则共49条。

4 GSA优化模糊PID的SVC系统参数

模糊PID进行SVC系统最优化控制时，模糊控制规则、量化因子以及比例因子都会影响SVC系统的控制效果，传统的方法是通过经验法获取控制参数，存在效率低下和效果较差的缺点，因此通过GSA算法优化量化因子和比例因子，可以实现SVC系统的最佳控制效果以及参数的自适应选择。

为实现模糊PID的SVC控制器的最优化参数选择，选择ITAE指标作为SVC控制系统的控制效果的评价指标,如式(12)[10-11]。

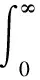
(12)

GSA优化模糊PID流程如图3所示。

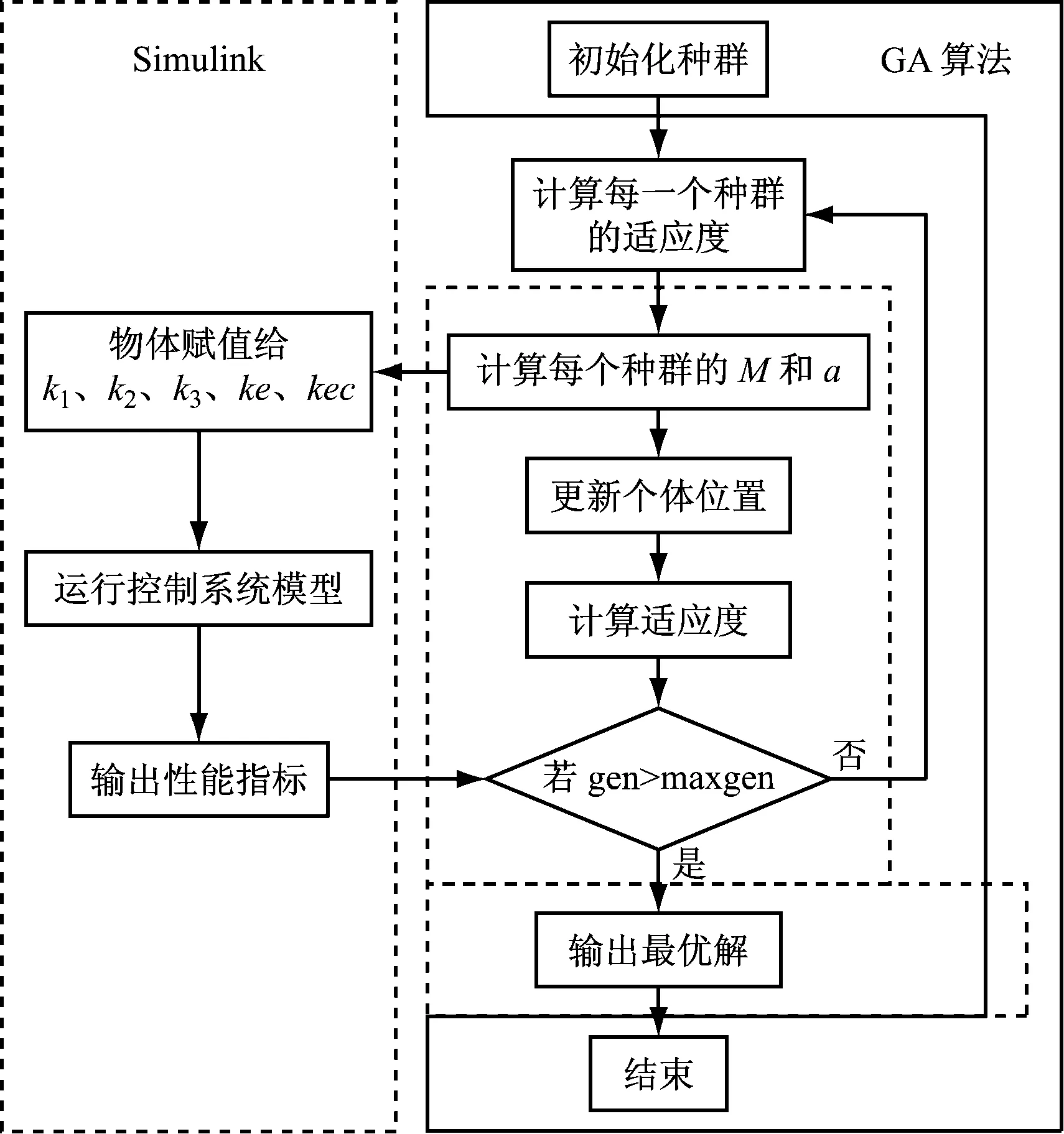
图3 GSA优化模糊PID流程图

其中k1,k2,k3分别是比例因子，ke,kec分别是量化因子。

其算法流程如下：

(1) 确定模糊控制的研究对象，其传递函数,为式(13)。

(13)

(2) 设定GSA算法参数：最大迭代次数iter，粒子数量N，初始化GSA算法所有粒子的位置和加速度；

(3) 根据式(12)计算每个粒子的适应度值，更新粒子引力常数；

(4) 根据式(3)和(4)计算粒子加速度和速度，在此基础上更新粒子的位置；

(5) 若满足停止条件，则输出最优解；反之，返回步骤(2)。

5 实证分析

为了验证本文算法的有效性，将GSA优化的模糊PID、常规PID和模糊PID进行对比分析，基于模糊神经网络的SVC控制框图,如图4所示。

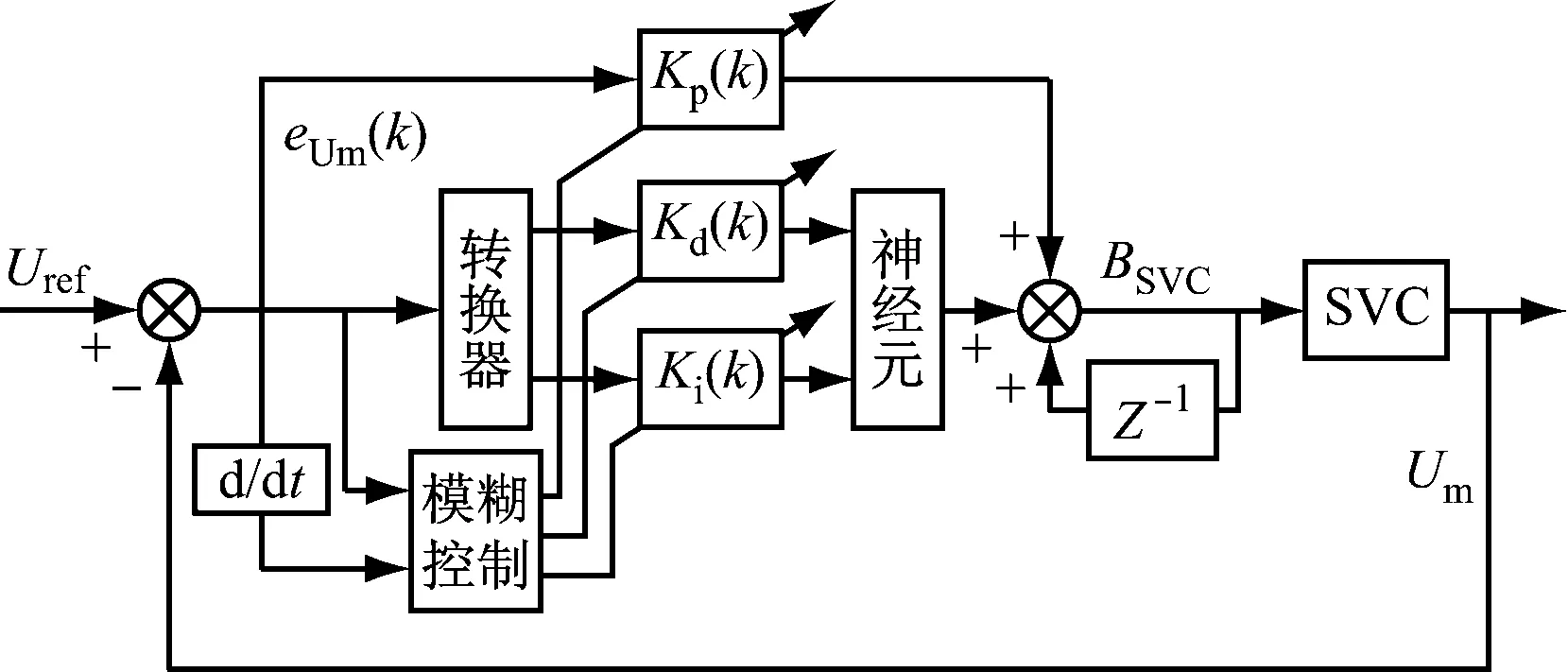
图4 基于模糊神经网络的SVC控制框图

5.1 仿真结果及其分析

设定GSA算法参数如下：最大迭代次数iter=50，粒子数量N=10，比例因子k1,k2,k3，量化因子ke,kec以及适应度函数寻优结果,分别如图5-图7所示。

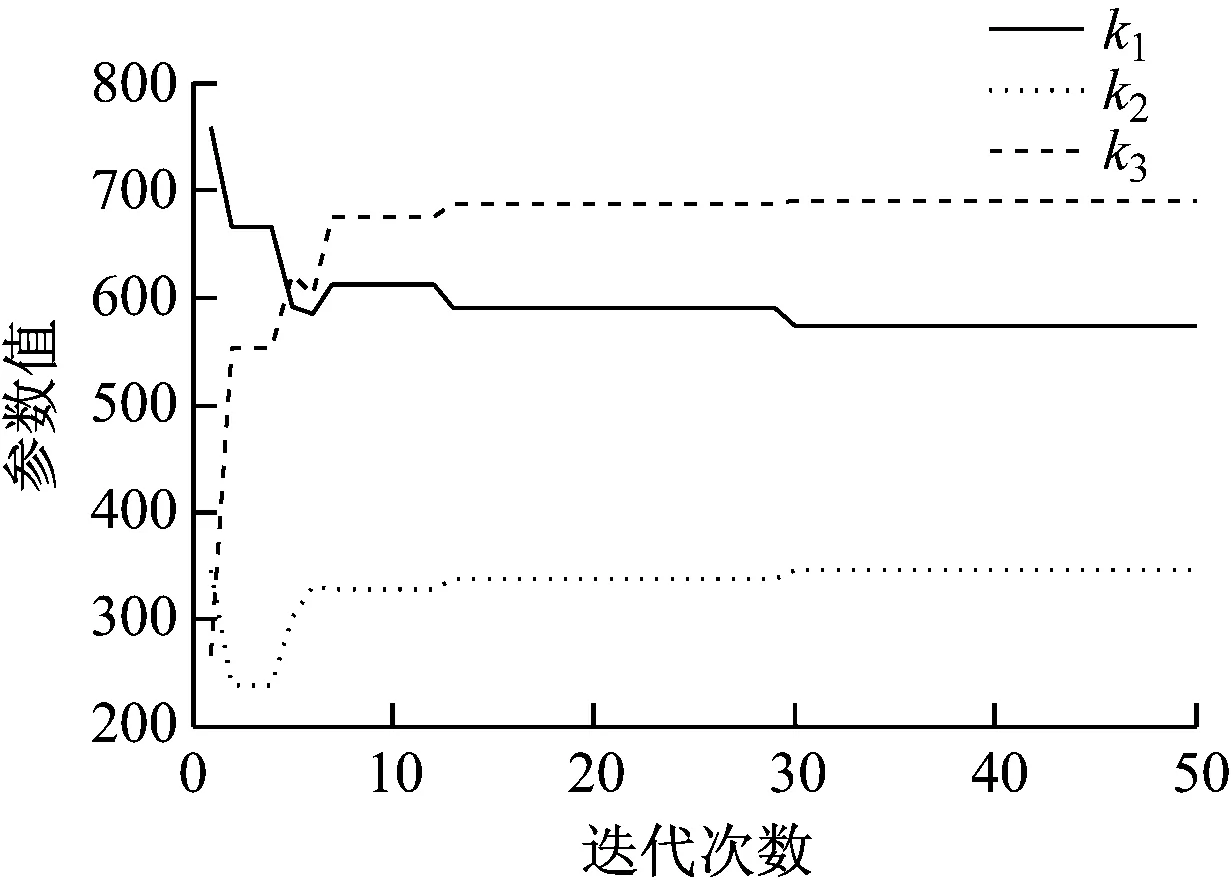
图5 k1,k2,k3的优化曲线

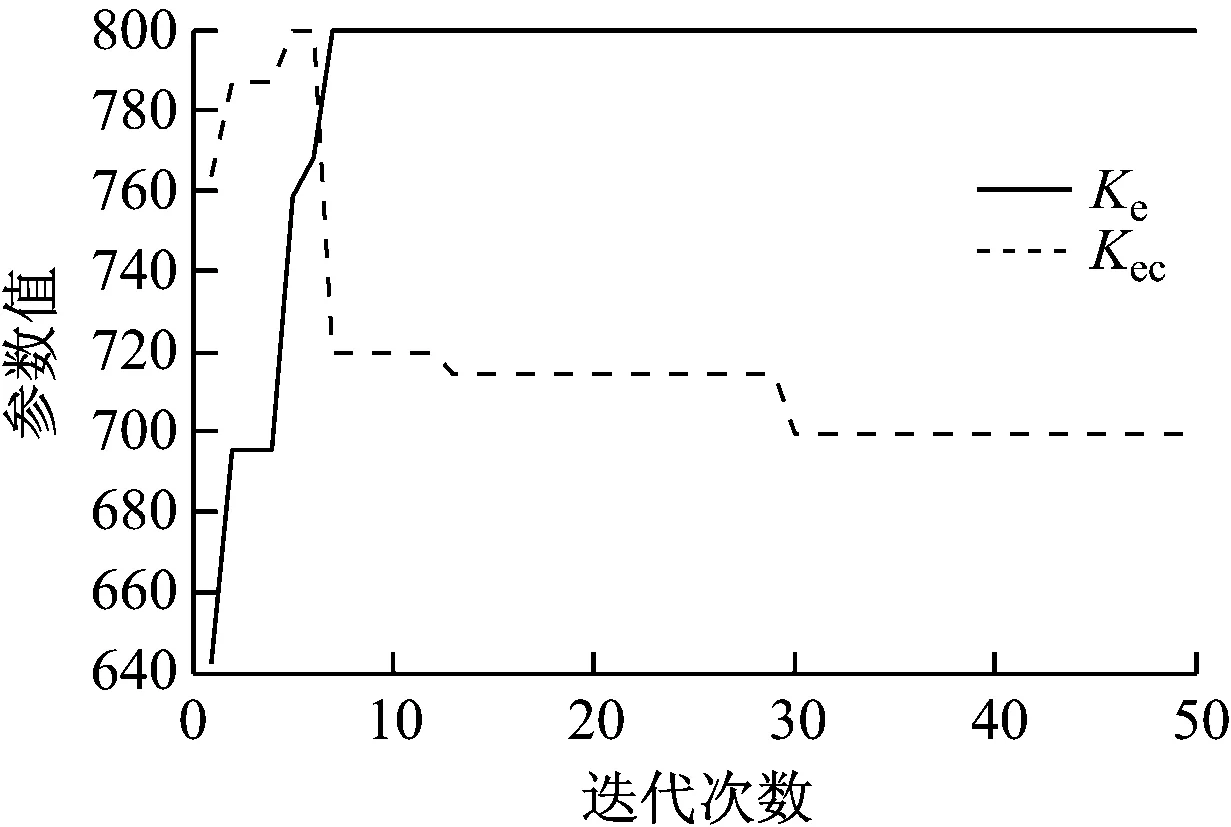
图6 ke,kec的优化曲线

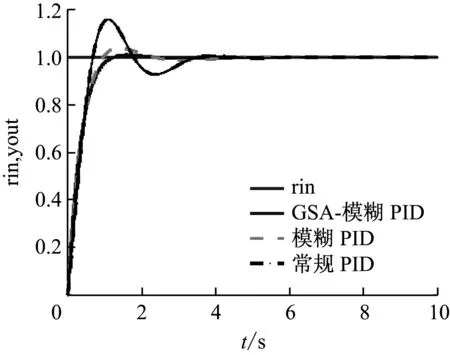
图7 阶跃响应输出曲线

系统的阶跃响应对比结果如图8所示。由图8可知，在超调量和响应时间方面，万有引力搜索算法GSA优化的模糊PID优于模糊PID控制和PID控制，具有超调量较小，响应时间较短的优点，进入平衡状态时间较短，控制品质较高，稳态误差较小。

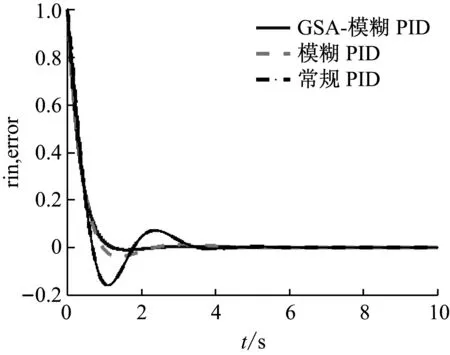
图8 阶跃响应输出误差曲线

6 总结

针对传统的SVC电压控制方法存在精度低和误差大的

缺点，提出一种基于引力搜索算法(Gravitational Search Algorithm，GSA)优化模糊PID的SVC的电压控制算法。实验结果表明，GSA-PID优化模糊PID和常规PID，实现SVC的最优化控制，本文算法具有更高的控制能力和超调量更小，稳态误差小的优点。

[1] 刘晓军, 杨冬锋, 高磊. 一类多静止无功补偿器阻尼控制器间的交互影响机理[J]. 电网技术, 2016, 40(2):534-540.

[2] 马力, 刘丽涛. 万有引力搜索算法的分析与改进[J]. 微电子学与计算机, 2015(9):76-80.

[3] 罗萍, 刘伟, 周述波. 自适应混沌变异的万有引力搜索算法[J]. 广东工业大学学报, 2016, 33(1):57-61.

[4] 李超顺, 周建中, 肖剑. 基于改进引力搜索算法的励磁控制PID参数优化[J]. 华中科技大学学报(自然科学版), 2012, 40(10):119-122.

[5] 周建中, 赵峰, 李超顺. 基于GSA的水轮机调速系统非线性PID控制参数优化方法研究[J]. 水电能源科学, 2014(12):127-130.

[6] 刘守明, 韩爱芝, 张之昊,等. 配电网静止无功补偿器设计及其并联运行策略[J]. 电力电子技术, 2015, 49(5):105-108.

[7] 周晓华, 罗文广, 刘胜永,等. 静止无功补偿器自适应动态规划电压控制方法[J]. 电网技术, 2017, 41(3):895-900.

[8] 张健. 静止无功补偿器抑制电网低频振荡的仿真研究[D]. 重庆大学, 2015.

[9] 周晓华, 刘胜永, 王荔芳,等. 静止无功补偿器的模糊神经元PID电压控制[J]. 电力电容器与无功补偿, 2016, 37(5):37-40.

[10] Bessette C R, Spencer D B. Performance Comparison of Stochastic Search Algorithms on the Interplanetary Gravity-Assist Trajectory Problem[J]. Journal of Spacecraft & Rockets, 2015, 44(3):722-724.

[11] Valdez F, Prado-Arechiga G, Prado-Arechiga G. Fuzzy logic in the gravitational search algorithm enhanced using fuzzy logic with dynamic alpha parameter value adaptation for the optimization of modular neural networks in echocardiogram recognition[J]. Applied Soft Computing, 2015, 42(14):5839-5847.