基于CUDA架构的高速RGBD场景解析算法研究

沈超， 王斌， 吴晓峰

(复旦大学 信息科学与工程学院， 上海 200433)

0 引言

随着深度传感器的不断发展成熟，普通用户可以使用手机、廉价深度相机，例如苹果iPhone X、微软Kinect等设备获取周围场景的深度信息。深度信息可以反映周围场景的空间拓扑结构，是色彩信息的有力补充。根据获取的场景RGBD信息，可以对RGBD数据进行场景解析。这在场景识别，增强现实，三维重建等计算机视觉应用中有着重要应用。受场景复杂度、纹理噪声、光照条件等因素的影响，目前使用的场景解析算法还存在较多问题。

场景解析作为计算机视觉任务的前端一环，对算法效果和运算速度都有较高的要求。现有的高速场景解析算法[1-3]大多数只处理场景图像的色彩数据，没有考虑深度信息。而已有的面向RGBD场景的解析算法大多要对法向量、重力方向等进行计算优化，难以保证算法的实时性。另外，现有场景解析算法基本都难以达到30 Hz以上的运行速度。为此难以满足解析算法可以实时运行、面向RGBD场景的需求。

本文的主要工作是提出了一种新的高速RGBD场景解析算法。使用加入空间平滑约束和边缘支持、含深度信息的高速过分割算法，对场景的RGBD图像进行过分割，并将过分割块构成无向图。然后运用层级结构的多特征求权Felzen-Hutten算法[2]进行无向图图割优化，完成场景解析。本文在RGBD场景数据集上对算法进行了实验，并得出实验结果。接下来从整体架构和步骤细节两方面论述整个算法，之后进行实验验证，最后给出文章结论。

1 算法论述

1.1 整体架构

本文提出的算法整体架构主要分为两大部分，一是高速RGBD场景过分割，二是过分割块的层级图割归并，都在CUDA架构上实现。具体如图1所示。

整个算法的输入数据为场景的RGBD信息。每个场景的RGBD信息由色彩信息(RGB)和深度信息(D)两部分组成，具体为一组色彩与深度图像对。本文结合图像的色彩和深度四个维度的信息，首先运用提出的超高速过分割算法BSD-gSLICr，对场景图像对进行过分割，将图像分解为过分

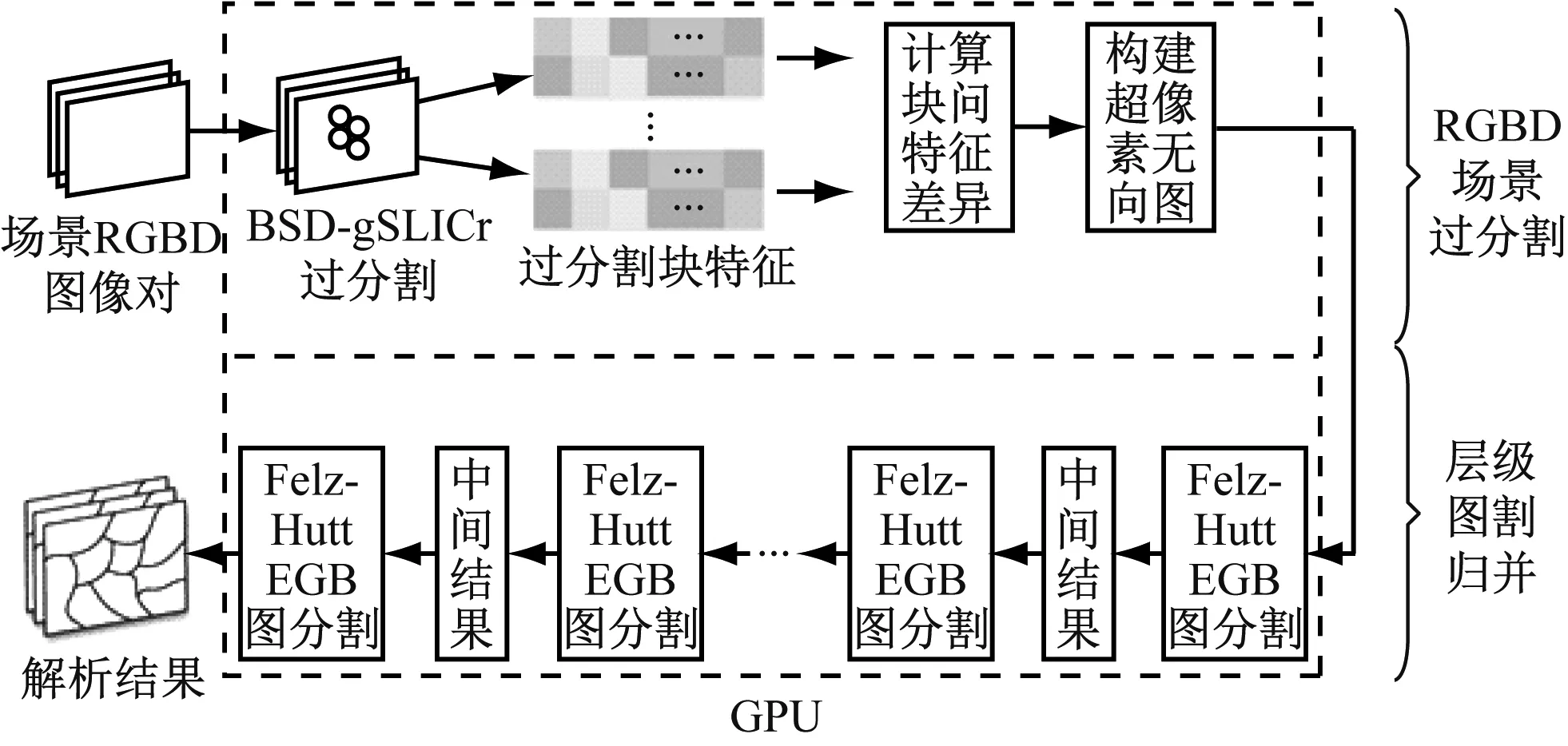
图1 算法整体框架

割块。然后将过分割块视为顶点，结合过分割块间相邻关系构建无向图，并根据块间特征计算相邻边权重。最后应用层次结构的Felzen-Hutten算法，对过分割块组成的无向图进行多层次图割分块，从而得到最终的场景解析结果。

我们之所以使用过分割与层级Felzen-Hutten图割的两步架构，一方面是利用BSD-gSLICr超高速的过分割能力，降低后续算法运算量，保证算法实时性，同时削弱噪声的影响。另一方面，对处理后的过分割块，采用层级结构的Felzen-Hutten算法进行图割归并，可以实现在不同层级注重不同的分块特征，从而应用不同的图割策略，这也具有现实的物理意义。总之，本文提出的架构在底层可以缓解噪声干扰，在高层可以改变算法策略，具有高度的灵活性和适应性。

1.2 步骤细节

1.2.1 BSD-gSLICr算法

本文提出的BSD-gSLICr算法是高速RGBD场景过分割部分的核心。2015年，牛津动视实验室开发了gSLICr算法[4]，在GPU上实现了250Hz的图像过分割速率。

本文在参考gSLICr架构的基础上，进一步引入场景深度信息，并添加了空间平滑约束。同时加入了边缘支持，减轻了空间信息比重增加造成的不利影响。我们精心设计了运算架构，用CUDA技术实现了BSD-gSLICr算法。具体如图2所示。

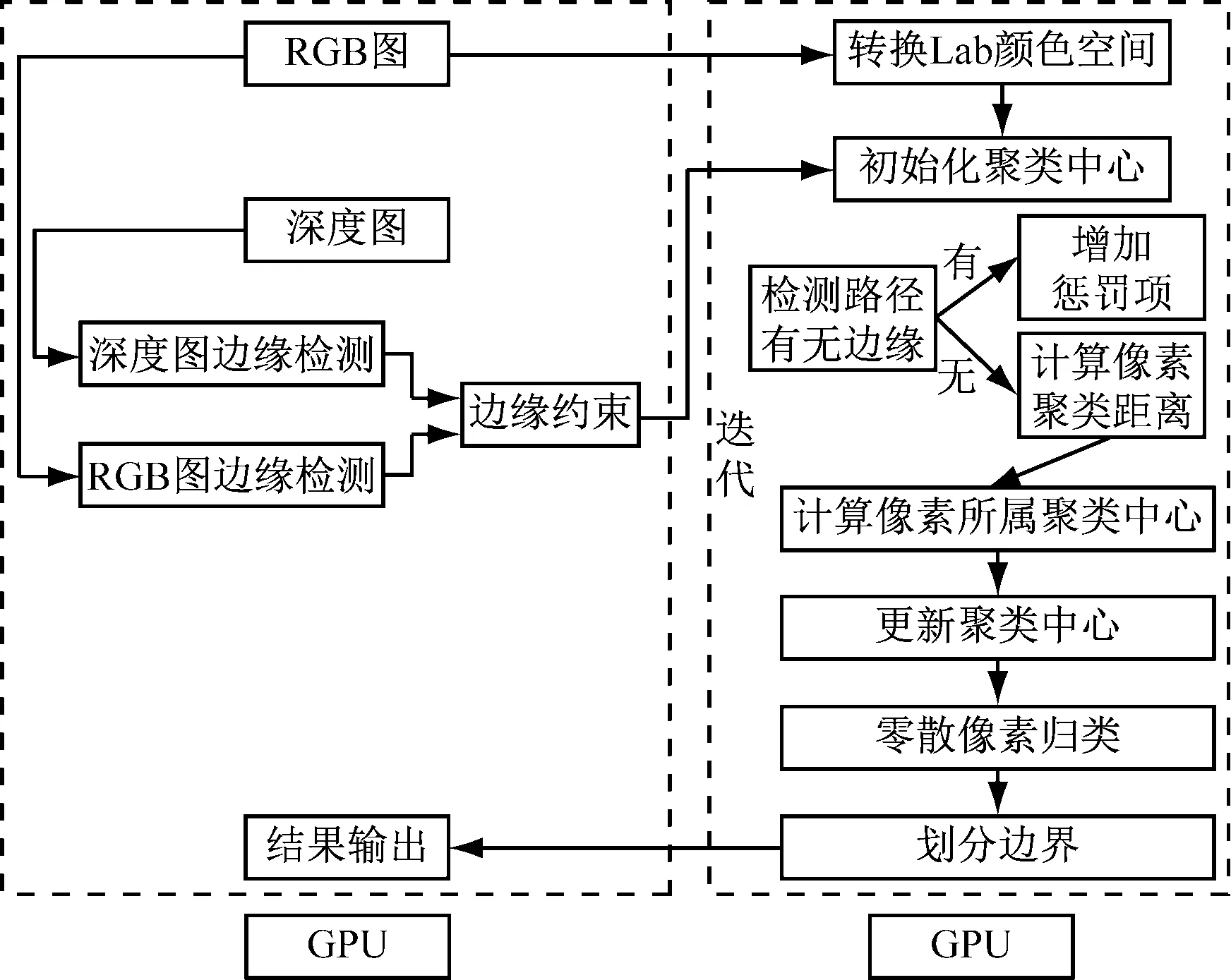
图2 CUDA架构下实现的BSD-gSLICr算法流程

除了读取图像部分，其余操作步骤都在GPU上处理。

(1) 空间平滑约束

gSLICr算法本质是一种快速SLIC算法[5]，通过对像素点进行聚类形成超像素，达到过分割图像的效果。gSLICr算法中的距离度量公式决定了像素聚类策略，是整个算法的关键。我们在距离度量公式中，加入了场景深度信息，并创新地添加了三维空间平滑约束项，以提升分割效果和鲁棒性。具体改进的距离度量式如式(1)～式(4)。

(1)

(2)

(3)

(4)

其中dc、ds分别为像素点与聚类中心间的lab色彩空间距离、xy坐标位置距离。dge为像素点深度距离，其中根式内第一项即为添加的三维空间平滑约束，式中cn,fn是场景拍摄相机的内参。D为像素点到聚类中心的总加权距离，其中N是像素总数量，K是聚类中心数量，m为紧密度，λ为深度信息权重。

(2) 边缘支持

由于距离度量公式中添加了深度信息，增强了空间因素在像素聚类中的作用。这导致图像中某些实体间的颜色边缘会因为深度信息的干扰被聚类到同一个块中，这对后面场景解析中具体实体的分割有较大影响。为此，在算法中引入了边缘支持。分别对RGB图像和深度图像，用canny算子检测边缘，合并形成边缘支持图。同时在距离度量公式中加入惩罚项如式(5)、(6)。

Dbs=D+Penalty(path((x,y)->(xc,yc)))

(5)

(6)

根据像素点与超像素中心的方位，采用分段的曼哈顿式折线形成连通路径。如图3所示。图3如果路径上存在边缘支持点，则在距离公式中添加惩罚项，使得像素点不会聚类到边缘另一边的超像素中心。这可以改善添加深度信息以后，聚类时空间因素过度优先的问题。

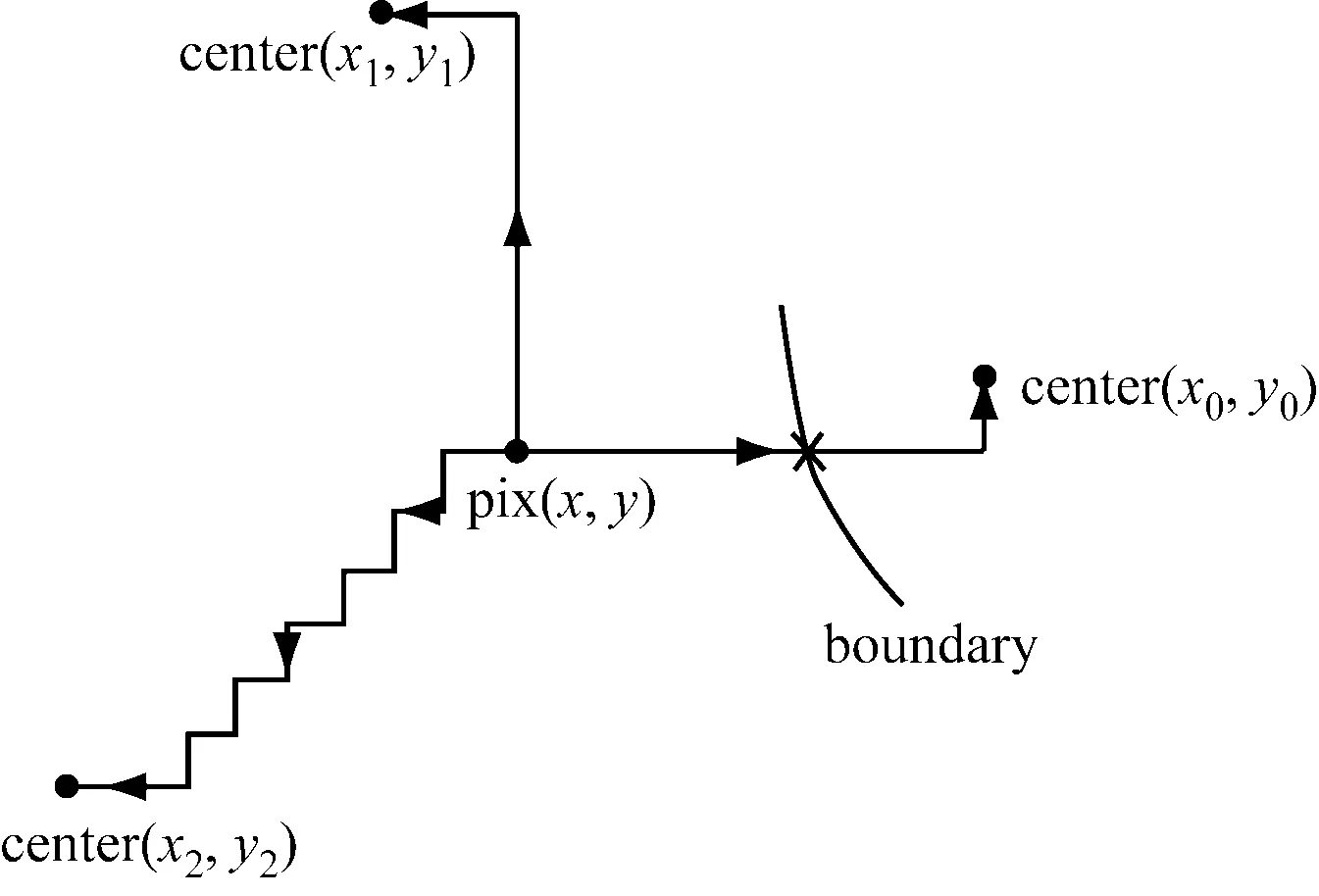
图3 根据像素点和超像素中心选择连通路径的选择

1.2.2 层级Felzen-Hutten图割归并

在第一部分，场景RGBD图像对BSD-gSLICr算法被分解为了超像素的过分割块。我们把每个过分割块看作一个顶点，块间相邻关系作为边，邻接块特征的不相似程度作为边权值，形成一个以超像素的过分割块为单位的无向图。并采用层次结构的Felzen-Hutten算法对无向图进行快速图割归并，完成超像素分割块的聚类，达到高速场景解析的目的。

Felzen-Hutten算法伪代码如下：

Felzen-Hutten算法：

输入：超像素无向图G=(V,E,W)，

输出：分割结果S=(C1,…,Cr)

初始化:将所有边权值w按从小到大排序P=(w1,…,wm)

forq=1,…,mdo

for eachwq=w(vi,vj) do

end if

end if

end for

end for

原始的FH算法中，无向图中边的权值只由相邻分块间的均色差异来决定。我们在RGBD场景解析的背景下，提出了新的边权值计算方法。充分利用RGBD场景提供的深度信息，在相邻分块间均色差异的基础上，引入边缘均色梯度、边缘均深梯度、分块位置差异，来共同决定相邻边的权值。其中，分块均色差异distmc计算相邻过分割块间的平均lab空间颜色距离，

distmc(sp1,sp2)=‖mColorsp1-mColorsp2‖2

(7)

分块位置差异distmp计算相邻过分割块中心间的二维坐标距离，

distmp(sp1,sp2)=‖mPositionsp1-mPositionsp2‖2

(8)

边缘均色梯度mBGc计算相邻过分割块间共同边缘上，每个像素与周围像素的色差，如式(9)。

(9)

边缘均深梯度mBGd计算相邻过分割块间共同边缘上，每个像素与周围像素的深度差异，为式(10)。

(10)

相邻过分割块间总的边权值w，由上述四个部分加权组成，为式(11)。

(11)

其中加权权值ω根据预训练集，采用线性svm预测回归的方法训练得到。考虑到在过分割块归并整合的不同阶段，各个块特征的重要性也应该不同。所以对不同层的训练，采用上一层得到的结果更新数据集，然后进行训练得到每层特有的加权权值。

得到每层的边权计算公式之后，我们就可以使用层次结构的方式，逐次对过分割块组成的无向图，采用Felzen-Hutten算法进行优化归并。经层级Felzen-Hutten算法优化之后，最终可以得到场景的解析结果。

2 仿真结果

我们用CUDA架构实现了本文提出的算法并进行测试，测试平台使用的CPU为Intel i7-6700K,使用的GPU为NVIDIA GTX1070。我们在纽约大学深度场景数据集v2[6]、明德双目视数据集[7]等RGBD场景数据库上做了测试。我们与一些快速分割及场景解析算法进行了比较，主要包括经典的分水岭算法、Felzen-Hutten算法、MeanShift算法，以及近期出现的快速场景解析算法如FGBOS算法[8]、HFS算法。最后得到了实验结论。

2.1 场景解析效果及拓展性

(1) 在明德双目视数据库上对算法进行了仿真，效果如图4所示。

图4 明德双目视数据库算法测试结果

图4中从第2列至第7列依次为分水岭算法、Felzen-Hutten算法、MeanShift算法、FGBOS算法、HFS算法和本文提出的算法。

(2) 在纽约大学深度场景数据集v2中对上述算法进行了测试，部分场景解析效果图，如下图5所示：

可以看到相对其他方法，本文提出的算法能够对复杂场景进行有效分解，分离出其中的具体实体，取得较好的场景解析效果。同时可以看到，本文提出的算法相对其他算法，能较好地避免过分割和欠分割现象，对于各个完整实体的区分度也更高。

另外，由于综合考虑了色彩和深度信息等多个特征，本

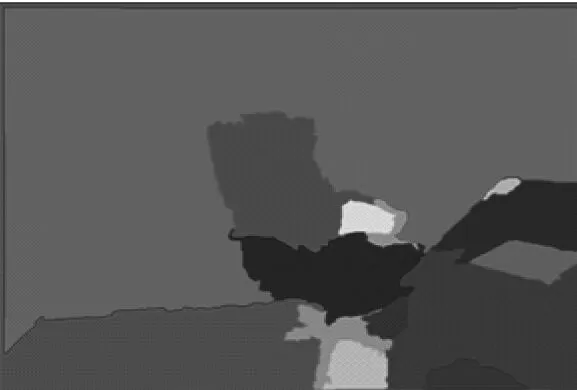
图5 Nyu Depth Dataset v2数据库算法测试结果

文提出的算法不易受到高频纹理变化的干扰，例如对原始场景1中幕墙上的光点和桌面上的纹理就有很好的抑制作用。同时即使在光照条件恶劣，场景颜色区分度差的极端情况下，如原始场景2中，前景物体与背景几乎难以区分，本文提出的算法在其他算法几乎失效时，场景解析的鲁棒性依然较强。

值得指出的是，本文算法根据应用场景的不同，也可以方便的拓展到单张RGB场景图像或单张深度场景图像上。例如在只有场景深度信息时，在BSD-gSLICr算法分割部分，只需根据场景深度图像检测边缘，计算(2)、(3)两式，同时将(4)式修改为式(12)。

(12)

然后在层级Felzen-Hutten图割归并部分，把边权值计算公式中的色彩特征项distmc、mBGc消除，只计算深度特征项，并调整相应权值，将(11)式修改为式(13)。

w=ωmpdistmp(sp1,sp2)+ωdmBGd(sp1,sp2)

(13)

就形成了本文提出的算法针对单深度场景的简约版本。以此类推，只需将算法中深度信息项消除，也可以形成本文算法针对单RGB色彩场景的简约版本。当然可以根据需要，在简约版算法的边权值计算公式中，加入更多色彩或者深度的块特征项，以提高算法效果。

2.2 算法复杂度及运行速度

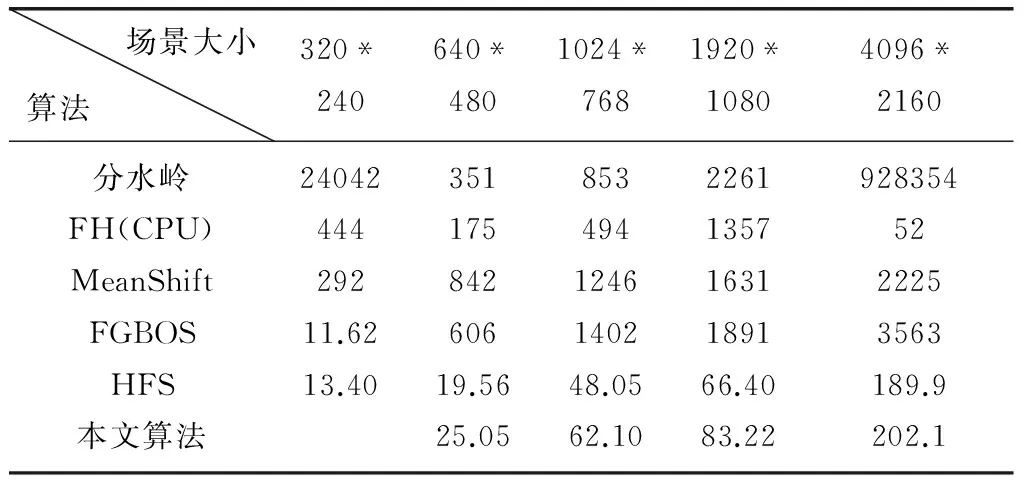
表1 不同算法平均运行速度(ms)

由表1可见，本文提出的算法由于在CUDA架构上经优化实现，在保证算法精度的前提下,速度有较大提高，与目前最快速的HFS算法基本接近。对于常见的640*480的图像分辨率，本文提出的算法运行速度平均在25 ms左右。特别在高图像分辨率的情况下，本文算法由于应用了过分割算法降低复杂度，相对传统算法速度有明显优势。由于满足实时要求，本文算法可以广泛应用在各类计算机视觉任务中，提升运算速度。

3 总结

本文提出了并在CUDA架构上实现一种新的高速RGBD场景解析算法。在gSLICr算法基础上，引入了带空间平滑约束的深度信息，并加入边缘支持，提出了BSD-gSLICr算法。并使用BSD-gSLICr算法对RGBD场景图像进行过分割，然后采用改进边权计算方式的Felzen-Hutten算法，将过分割块构成的无向图进行多层级的图割归并，得到最终的场景解析结果。在多个RGBD数据库上的实验结果表明，本文提出的算法兼具速度和效果优势。相对一些传统算法，在速度及效果上均有较大的提高。而与目前先进水平的算法相比，在处理高频纹理或者光照条件恶劣的场景时，本文算法也有独有优势。未来会针对场景深度信息缺失、噪声等情况，考虑添加置信度，进一步增加算法的鲁棒性。

[1] Cheng MM，YUN Liu, Qibin Hou. et al. (2016) HFS: Hierarchical Feature Selection for Efficient Image Segmentation[C]∥Eccv 2016 Amsterdam Netherlands. Lecture Notes in Computer Science[M]. V. 9907. Springer.

[2] Felzenszwalb PF, Huttenlocher DP. Efficient graph-based image segmentation[J]. IJCV, 2004,59(2), 167-181.

[3] Jean Cousty, Gilles Bertrand, Laurent Najman, and Michel Couprie. Watershed Cuts: Minimum Spanning Forests and the Drop of Water Principle[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2009, 31(8): 1362-1374.

[4] Ren, Carl & Prisacariu, Victor & D Reid, Ian. gSLICr: SLIC superpixels at over 250 Hz[R]. arXiv preprint arXiv:1509.04232,2015.

[5] Achanta R, Shaji A, Smith K, et al. SLIC Superpixels Compared to State-of-the-Art Superpixel Methods[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 34(11): 2274-2282.

[6] Silberman N, Hoiem D, Kohli P, et al. Indoor Segmentation and Support Inference from RGBD Images∥Lecture Notes in Computer Science (vvl 7576)[M]. Berlin: Springer.

[7] Scharstein, C. Pal. Learning conditional random fields for stereo[C]∥In IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR 2007), Minneapolis, 2007.pp1-8.

[8] Toscana G, Rosa S, Bona B. Fast Graph-Based Object Segmentation for RGB-D Images[C]. Intellisys 2016, London, UK. pp42-58.