基于自适应方法的移动机器人同时定位与地图构建研究
陈群英
(西安培华学院,西安 710125)
0 引言
机器人就是将传感器、微电子、计算机等新技术为一体的产物,移动机器人在 20 世纪 60 年代初期诞生,通过50多年的发展,得以广泛应用到人类生产、生活多个方面,展现出强有力的生命力。由于机器人应用领域日益扩展,多数学者加大对于机器人控制方法及技术方面的研究。20世纪中后期,多项研究集中在如何基于高速度、重载条件下提升跟踪精度等方面。随着计算、信息融合等技术的快速发展,机器人技术也得到迅速的发展,尤其是在具备移动行走功能、环境感知能力的移动机器人研究也成为机器人技术领域研究的热点问题。不得不说,移动机器人自主研究已经获得显著进步,它不单为人们生产生活提供自动化设备,且在医疗卫生、排险救灾等领域发挥着重要的作用。例如:汽车生产领域主要工作在于做好焊接、搬运、零件组装等工作的机器人;处于水下、地下等恶劣条件下用于资源探测、矿难救灾的机器人等。对移动机器人而言,具备自主导航能力则是移动机器人走向具体应用的前提条件。同时定位与地图创建(Simultaneous Localization and Mapping, SLAM)就是指在未知的环境下,机器人可依托自身传感器对周围的信息进行测量,以此评估自身位置及运动状态,并能真实描绘周围环境地图的过程[1]。移动机器人SLAM相关问题研究旨在探究机器人处于陌生的环境下,可以自主识别环境内的特征信息,并运用所获取的特征信息创建周围环境地图模型,机器人能够依据所构建的模型实施定位和导航。本次研究就是对同时定位与地图创建多种算法展开研究,并基于传统方法进行适当改进,以此提升 SLAM 工作性能及精确度。
1 应用RBPF开展地图构建
1.1 粒子滤波
粒子滤波器又被称作Monte Carlo定位方法,这是一种统计滤波算法,也是保障Monte定位法顺利实现的方法。它开展滤波处理的思想在于贝叶斯采样估计对序列重要性进行采样处理,粒子滤波器无需直接求得概率密度函数,而是通过粒子集合对概率分布情况进行描述[2]。如果粒子样本数量处于无穷大状态,其作为能够逼近任意形式的概率分布,它应用一组随机的离散粒子集对系统状态后验密度分布状况进行描述,粒子集越密集,说明这个区域概率更大。此外,粒子滤波器出现也为机器人具体定位提供有效地解决途径。它几乎能够用于各种机器人定位问题,粒子滤波算法则是有效解决SLAM最有效、成熟的方法。
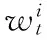
(1)
上述式子中,π(x1:t|z1:t,u1:t-1)称为重要性函数或建议分布。通过归一化处理后,重要性权值,如式(2)。
(2)
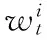
(3)
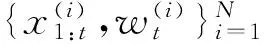
(4)
通过上述分析,地图后验概率具体估算如式(5)。
(5)
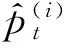
1)RBPF算法内蒙特卡罗环节要由先验环节实施采样处理为式(6)。
(6)
2)若将先检验分布作为重要性函数,如:π(x1:t|z1:t,u1:t-1)=p(xt|xt-),以此开展递归计算为式(7)。
(7)
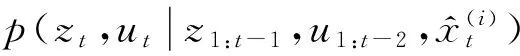
1.2 卡尔曼滤波
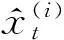
上述式子中:
利用在均值及方差更新环节中,应用卡尔曼滤波器,RBPF算法估算精度明显提升。随后,RBPF算法必须对每个粒子运用卡尔曼滤波器,如果存在多数粒子时,求解复杂程度会显著增加。
2 改进后的RBPF算法
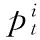
(1)标准RBPF的卡尔曼更新操作如下:
fori=1 toNdo
end for
(2)改进后RBPF卡尔曼更新步骤:
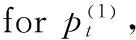
fori=2 toNdo
end if
end for
在此基础上,建议应用文献中的
作为间距,由采样环节内应用自适应重采样技术,通过采样、求解粒子重要性权值、更新地图等步骤,顺利实现同步定位与地图构建。
经改进处理的流程,如图1所示。
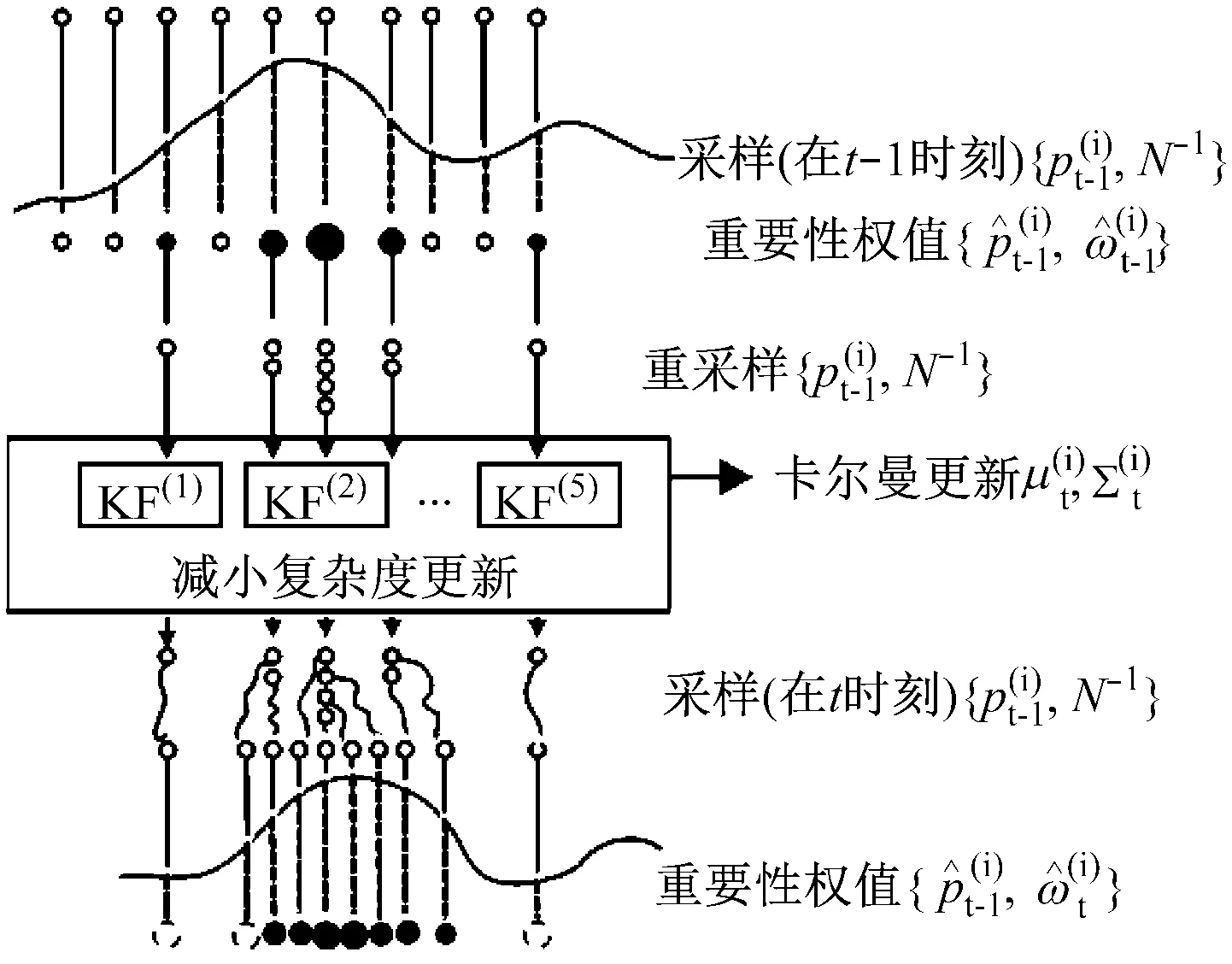
图1 改进RBPF算法实现流程
3 应用实例及结果分析3.1 实验环境及平台
所用平台采用装配URG-04LX激光测距仪器的PioneerIII-DX机器人,配置2.19GHz的GPU、内存达到1.96GB的笔记本电脑组合而成。实验所用的电脑按照Ubuntu 12.04操作系统及Groovy版ROS,通过笔记本恰当控制机器人运动状态,如图2所示。

图2 实验应用平台
实验环境选择某学校研发中心一楼,如图3所示。


图3 实验环境
3.2 实验结果
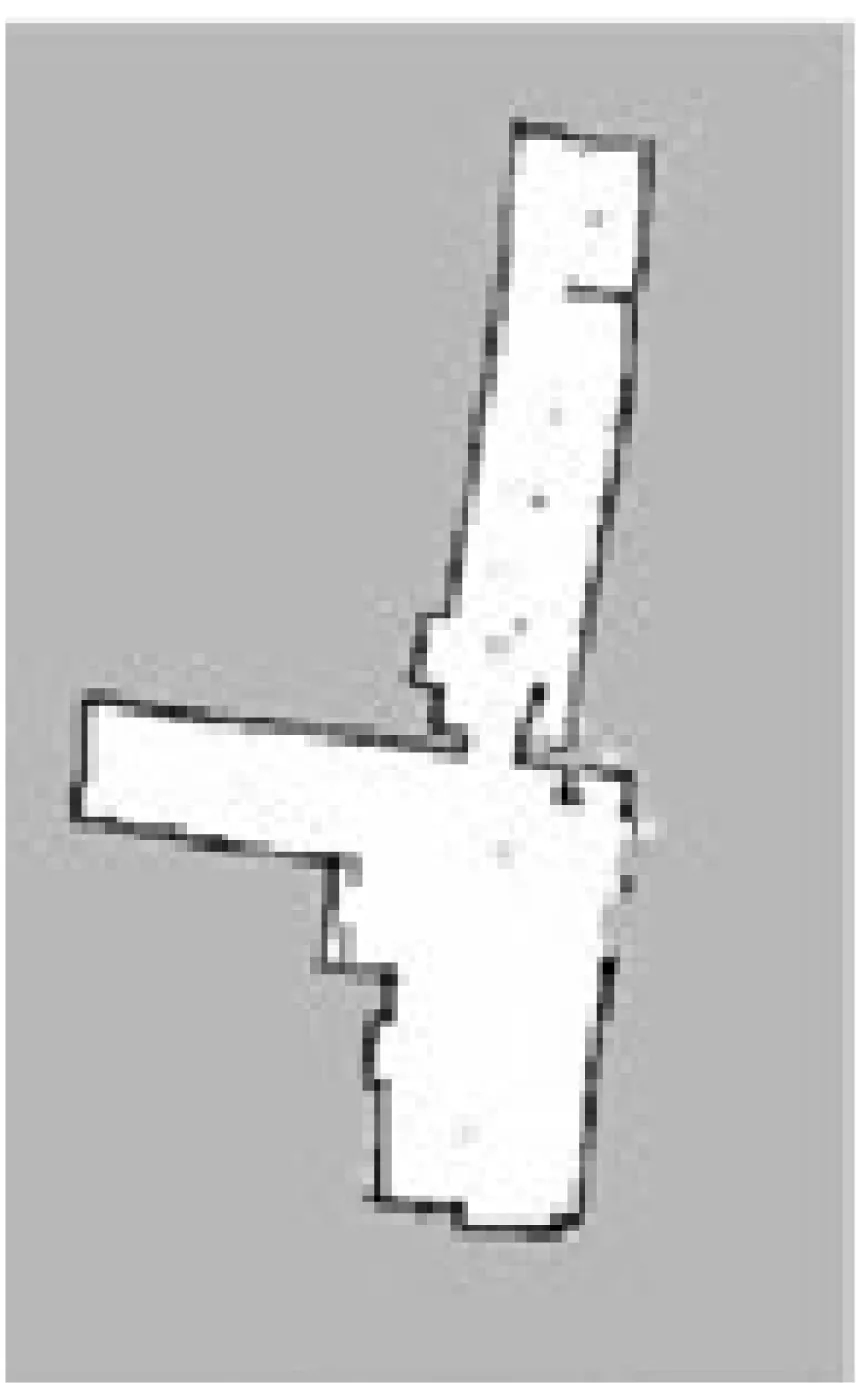
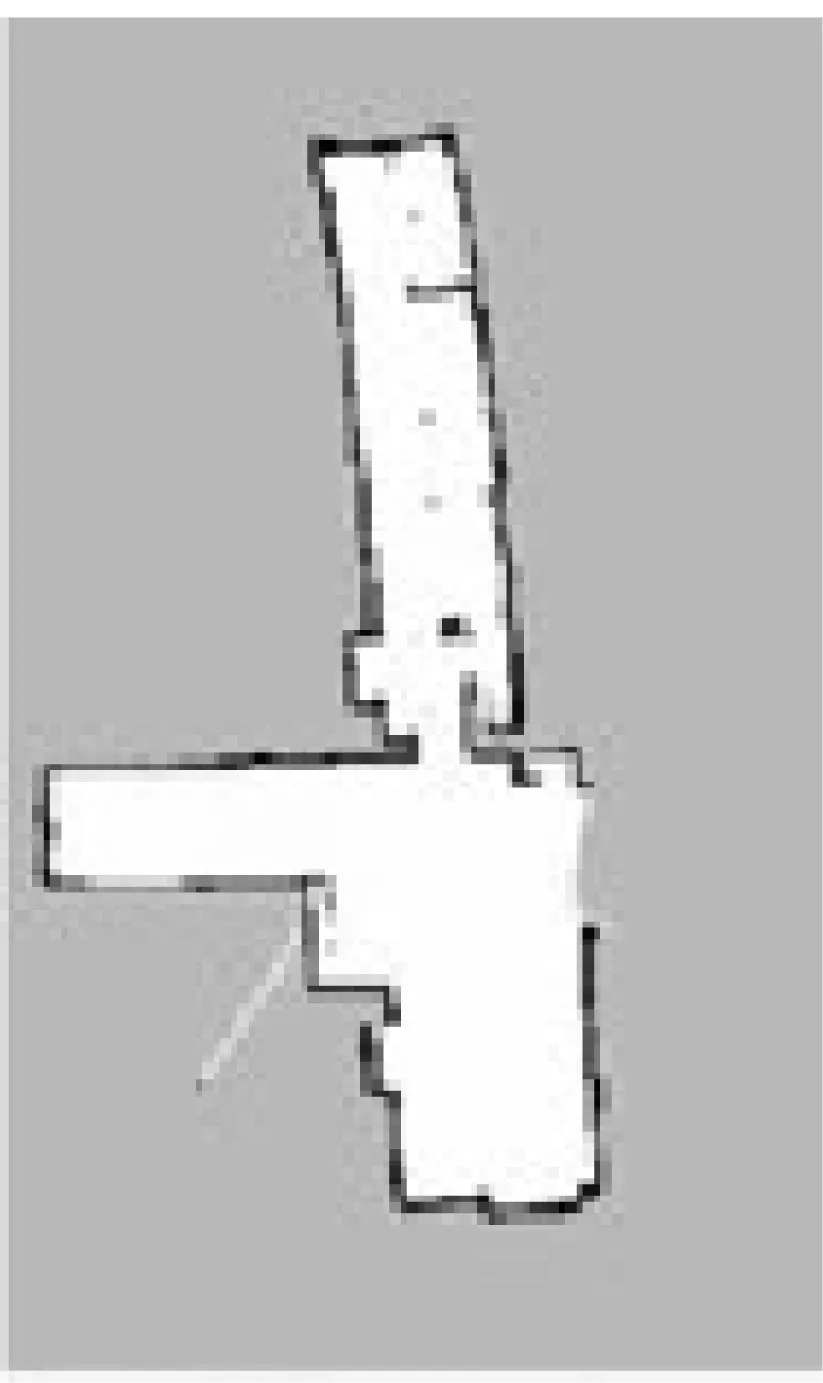
对于同步定位与地图构建过程中,总时间消化与机器人运行速度、环境存在密切的联系,算法详细的时间消耗很难确定。但可以利用控制机器人运动速度,进一步评估算法的实时性。若所用算法复杂程度较大,整个计算过程需要耗费大量的时间,较快的运动速度使得地图精度明显降低,必须适当放慢运动速度,以确保所得地图的精度[10]。当算法复杂度较小,计算所用时间也会有所减小,较快运动条件下也能确保地图的精度[11-12]。两组算法均运用120个粒子,每一种算法每种速度当作一组开展10次实验,共接受60次实验,每一组首次试验中设定机器人原地运行,获得地图的同时把所观测出来的里程和激光数据记录到bag文件内。剩下9次实验应用该文件内的数据实施仿真处理,获得与之相应的地图,bag文件具有ROS设定的文件格式,能够把不同类数据信息保存在同一个文件中,得以广泛用于测试算法中。运用bag文件展开算法调试工作,能确保每一组实验数据的一致性,进而减少误差。实验结果证实,每组实验均展现出共同的特性,挑选具有代表性的结果展开对比分析。不同运动速度条件下Gmapping算法和改进算法绘制出来的地图,如图4、图5所示。
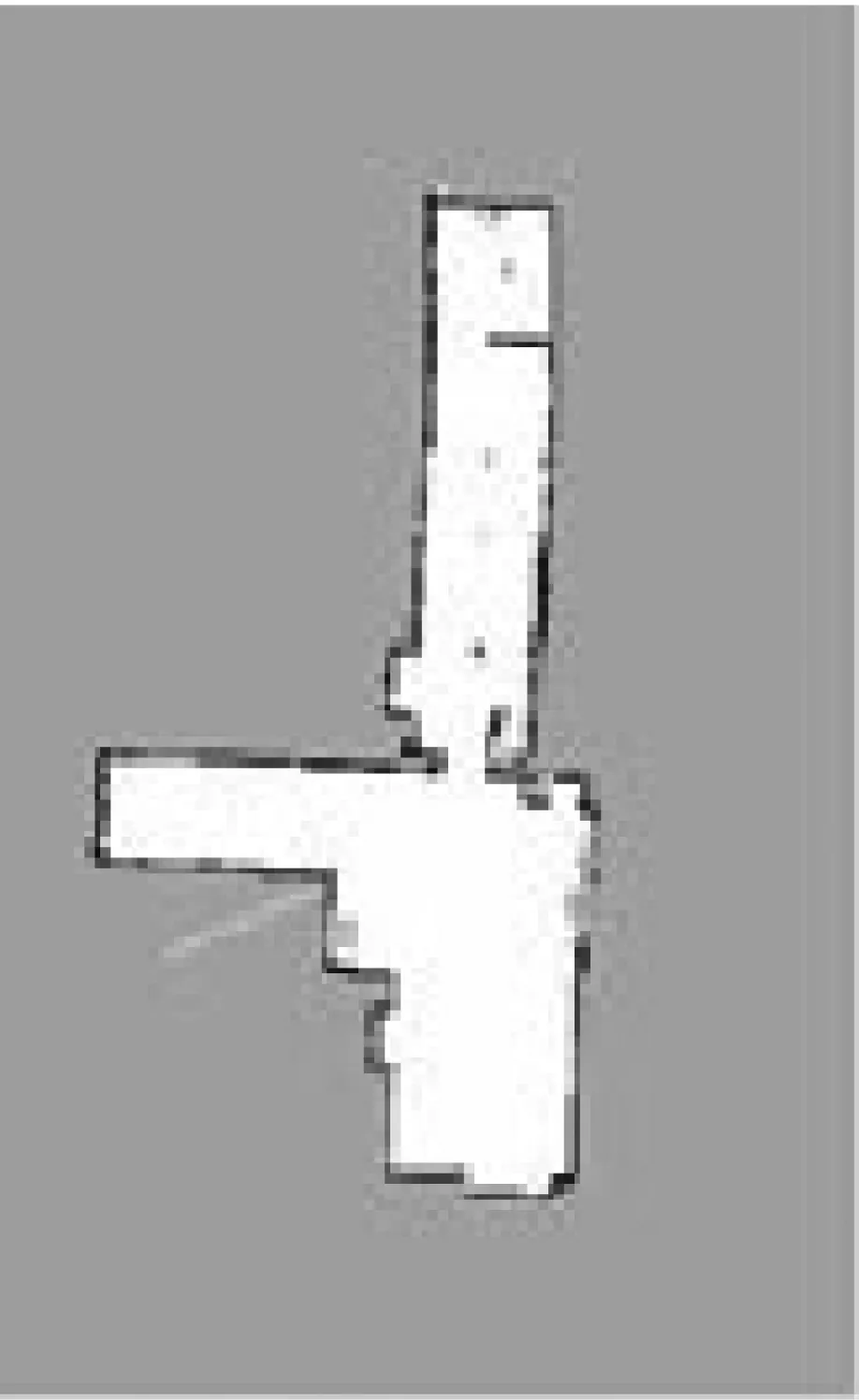
(a) 0.2 m/s
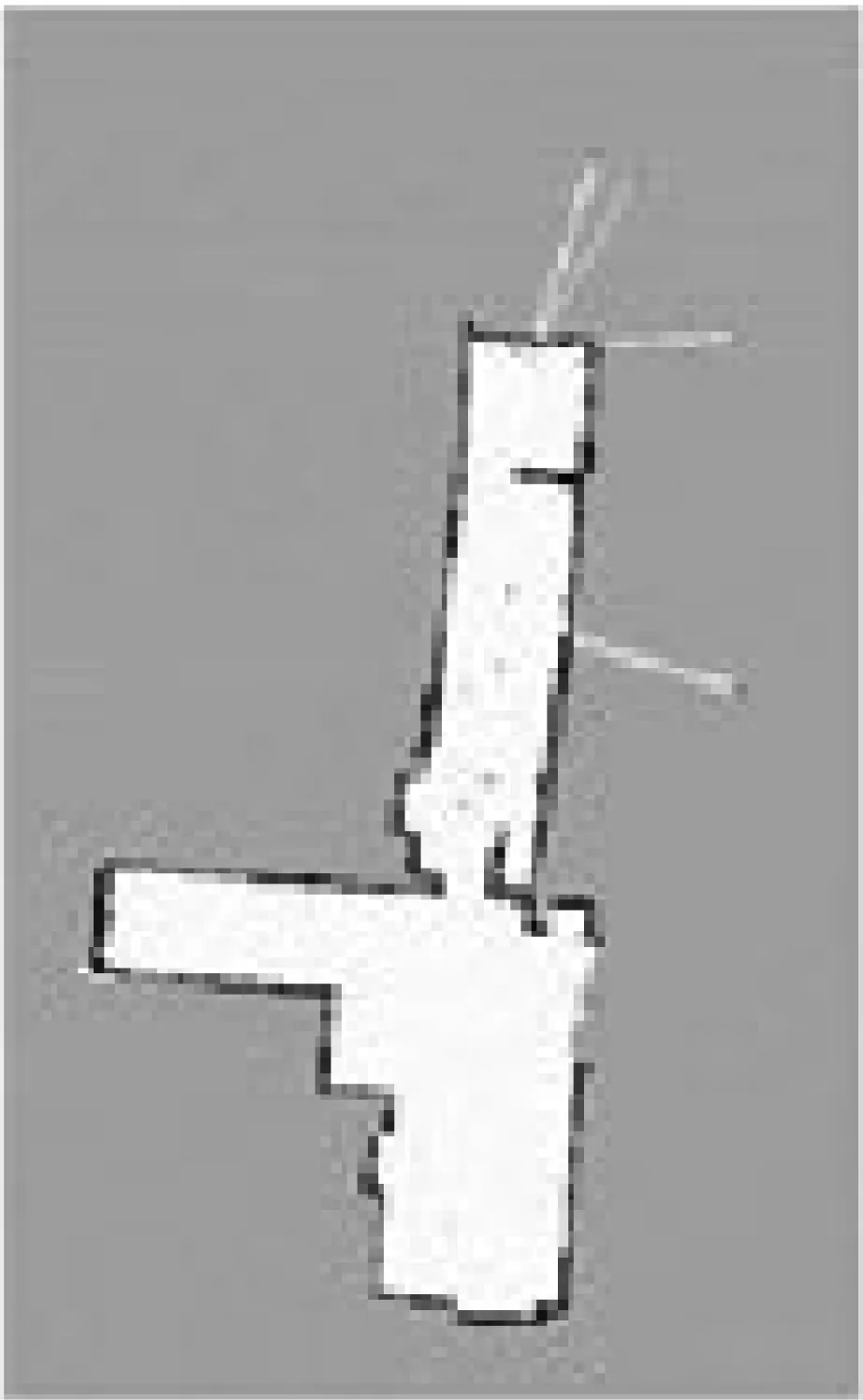
(b) 0.4 m/s

(c) 0.8 m/s
(a) 0.2 m/s

(b) 0.4 m/s
(c) 0.8 m/s
通过实验可知,上述两种算法由于机器人运动速度加快,都会出现栅格误差不断增大、地图质量降低的情况。当运动速度处在0.2 m/s时,两种算法均可以创建相对稳定的地区,而在0.4 m/s运动速度时,应用Gmapping算法就是个发展误差,且地图存在不确定性的特征,改进算法算法并未出现误差。处于0.8 m/s运动状态时,为改进前所用算法绘制地图误差增加,改进后所用算法也存在一些误差,但整体效果明显比改进前好,表明利用改进算法,其在各种运动速度条件下,创建的地图更稳定,边缘清晰度更高。
4 总结
综上所述,移动机器人同时定位与地图创建作为机器人顺利实现自主导航的关键,本文对于移动机器人同时定位与地图创建问题的多种方法展开研究,旨在探讨如何提升移动机器人自主能力。文章提出一种改进 LMNO 算法应用到移动机器人SLAM,依托卡尔曼滤波器更新某个特定条件下一组粒子中的代表粒子。必要情况下,对其均值、方差实施更新处理,并在同一个粒子群内重复运用,进一步降低操作复杂度,提升所用系统实时性。在此基础上,选择Pioneer III-DX机器人操作平台下展开实验,实验结果表明,改进RBPF算法,其运用不同运动速度下,所创建的地图比较稳定,具有清晰地边缘。
[1] 闫德立,宋永端,宋宇,等.平方根容积卡尔曼滤波概率假设密度算法在移动机器人同时定位与地图构建中的应用[J].控制理论与应用,2014,31(8):1009-1017.
[2] 丁少文,王林.基于连续三角测量法的机器人定位方法[J].微型电脑应用,2013,30(5):9-12.
[3] 赵亮,陈敏,李洪臣,等.基于视觉同时定位与地图构建数据关联优化算法[J].计算机应用,2014,34(2):576-579.
[4] 陈鹏慧,蔡琼,彭华顺,等.基于遗传算法的多移动机器人协同调度方案[J].微型电脑应用,2016,32(7):34-38.
[5] 伍明,张国良,李琳琳,等.基于动态和静态环境对象观测一致性约束的移动机器人多传感器标定优化方法[J].兵工学报,2017,38(8):1630-1641.
[6] 罗元,苏琴,张毅,等.基于优化 RBPF 的同时定位与地图构建[J].华中科技大学学报(自然科学版),2016,44(5):30-34.
[7] 罗元,傅有力,程铁凤,等.基于改进Rao-Black wellized粒子滤波器的同时定位与地图构建[J].控制理论与应用,2015,32(2):267-272.
[8] 蔡炯.机器人自适应主动同时定位与建图新方法[J].计算机测量与控制,2015,23(5):1639-1642.
[9] 叶锦华,李迪,叶峰,等.输入受限的非完整移动机器人的自适应模糊控制[J].中国机械工程,2014,25(8):1010-1016.
[10] 王丽佳,贾松敏,王爽,等.采用改进Mean Shift算法的移动机器人行人跟踪[J].光学精密工程,2013,21(9):2364-2370.
[11] 葛媛媛,张宏基.基于自适应模糊滑模控制的机器人轨迹跟踪算法[J].电子测量与仪器学报,2017,31(5):746-755.
[12] 于涛,赵伟,孙汉旭,等.一种球形移动机器人爬坡运动的自适应滑模控制[J].测控技术,2017,36(7):60-65.

