基于潜在缺陷暴露增益的可靠性试验设计规划模型

邵 恒, 方志耕, 张 秦, 刘思峰,2

(1. 南京航空航天大学经济与管理学院, 江苏 南京 211106;2. 德蒙福特大学计算机智能研究中心, 莱斯特 LE19BH)

0 引 言

装备的实际工作使用环境对装备的可靠性具有很大的影响,不同的环境严酷程度条件下,系统的可靠性水平可能表现为不同的值,因此目前针对可靠性试验的模拟环境越来越向实际使用环境靠拢,甚至于直接在实际环境中进行测试,对于装备的可靠性试验要求也逐渐提升。同时,由于装备系统的集成度和复杂度越来越高,试验成本不断提升,如何针对装备系统的可靠性试验进行科学合理的设计与规划,在试验前对预期结果就有一定的估计,从而提高可靠性试验的水平,是备受国内外学者关注的重要问题。

针对如复杂装备系统等价值高、试验较为困难的产品,学者们主要研究了其可靠性试验的样本量或试验时间优化问题。文献[1]考虑了弃真风险和采伪风险建立了基于信息融合的可靠性试验优化设计模型,在融合了系统层和子系统层信息的基础上给出了最优化试验方案。文献[2]依据Bayes理论,对可靠性参数服从指数分布的产品系统进行了可靠性统计试验设计,以验后期望损失最小为目标给出了最短试验截止时间的计算方法。文献[3-6]分别针对数控机床、轮轨等产品进行了可靠性试验分析设计,分别解决了对应领域产品可靠性评估试验最小截止时间与样本容量估计、试验周期以及试验因子与试验装置设计的难题。文献[7-8]针对高可靠性与长寿命产品提出了一种基于广义逆高斯过程的步进应力加速退化试验方法,在试验费用、样本量以及试验时间等约束条件下探讨了步进应力退化试验的优化配置解。考虑到加速寿命试验具有样品失效快、样本量小以及统计方法相对成熟的特点,文献[9-10]分别对多个应力水平的恒定加速寿命试验进行了设计;文献[11-12]分别针对新型航空航天用光电耦合器和大功率LED灯设计了加速试验方案,取得了较好的效果;文献[13-14]基于维纳退化过程模型开展了加速退化试验的优化设计,并给出了确定的应力水平的加速退化试验方案。从可靠性试验的环境因素角度考虑,文献[15]研究了温度、湿度、振动3种环境因素分别施加和综合施加到产品上的效果,探讨了3种环境试验技术在产品可靠性试验领域的应用；文献[16]提出了包含高线加速度、振动、温度等五参数的综合环境试验样机的研究技术方案,对方案实现的几个关键性问题进行了分析并给出了解决办法。

但是,纵观诸多可靠性试验优化设计研究内容,仍有不足之处:一是仍然局限于对试验的样本量、试验时间等进行优化以及多来源信息的融合利用方面,缺乏对系统及子系统的可靠性试验进行总体规划的理论;二是未将装备的实际工作环境因素作为变量之一纳入考虑,逻辑上略显不完备。为此本文从可靠性试验目的角度出发,提出了基于潜在缺陷暴露增益的可靠性试验设计规划模型(reliability test design planning model based on potential defect exposure gain,RTDEG),主要优势有:

(1) 首先提出了系统潜在缺陷暴露增益的概念,从可靠性试验的缺陷暴露效果角度对试验进行评估,提供了一种新的可靠性试验评估视角;

(2) 从装备的实际工作环境角度入手,考虑试验的全面程度与严酷程度,可在试验费用等条件的约束下,取得潜在缺陷暴露增益最大的目标。该增益包含内容为落实到系统的哪种环境因素需要进行试验、系统的各个环境试验因素的试验应力水平为多少比较合适等;

(3) 在复杂装备研制采用的主制造商-供应商模式下,各供应商的子系统试验数据还可作为主制造商的系统级试验参考量。

最后通过具体的案例分析证明了本文中模型的有效性。

1 可靠性试验基本要素分析

1.1 可靠性试验环境因素分析

系统工作的环境是多种多样的,也是可以进行分类的[17]。假设其为可用参数化的形式来表示的一种因素,图1为各级系统与工作环境的对应关系,总系统共包含n(n=1,2,…)个子系统,可能的工作环境因素共有u(u=1,2,…)个,则可通过一定设备对系统工作环境进行模拟,从而进行系统的可靠性试验。同时,对系统而言,其与分系统工作时面临的环境既是相互独立的,又是一定程度上相似的,彼此之间仍存在一定区别。

图1 各级系统工作环境示意图Fig.1 Work environment schematic diagram of each level system

由于可靠性试验的目的是验证系统的功能在一定环境因素下是否能够正常实现,因此试验与系统功能是分不开的。

定义1如果可靠性试验在某一环境下对系统的所有功能进行了试验,称试验覆盖了该环境。

下文中提到的在某一环境因素下的可靠性试验,均为系统的所有必要功能都在该环境下进行了测试。

1.2 可靠性试验目的分析

可靠性试验的目的是为了发现、识别系统中潜在的缺陷,从而对系统进行评价[18]。因此,可靠性试验的最终目的是为了暴露系统的缺陷,使得系统可靠性得到提升。

但是,可靠性试验过程中的缺陷暴露以一定的概率发生,难以发现系统的所有潜在缺陷。因此,定义“潜在缺陷暴露增益”的概念,对产品的缺陷暴露效果进行测度,并以潜在缺陷暴露增益最大为试验目的之一进行可靠性试验的设计规划。

定义2系统的潜在缺陷暴露增益指在一定约束条件下(如试验总费用等),单位试验成本带来的潜在缺陷暴露效果,可用系统可靠度提升量与费用的商替代,用字母V表示。

(1)

式中,ΔR表示系统的可靠度提升量;C表示系统的试验总费用。

由于系统的可靠度提升量是与该系统可靠性试验的全面程度和严酷程度息息相关的,即ΔR=f(Q,S)。根据文献[18-19]中的相关定义,给出可靠性试验的全面程度和严酷程度的概念。

定义3系统的所有环境影响因素的试验覆盖程度,称为系统的可靠性试验全面程度,用字母Q表示。

定义4系统的可靠性试验中各环境因素应力水平对设计极限范围的覆盖程度,称为系统在各环境因素下的严酷程度,用字母S表示。

需要注意的是,全面程度Q表示对环境因素的覆盖程度,其是一个属于[0,1]范围内的量;同理,严酷程度S表示对某一环境因素的应力范围的覆盖程度,亦属于[0,1]范围内,详细的论证见第2节。

1.3 可靠性试验费用分析

根据广州某检测机构的《2012年环境与可靠性试验标准试验价格》标准,可以得到系统在各环境因素水平下的一般试验费用,如高温试验,在1 m3试验箱中,进行温度范围为室温至+150 ℃的试验时的单价为每试验台时60元。

因此,由同类型产品的试验费用经验公式,系统i在某一环境因素j下的可靠性试验费用(单位:元)函数为

Cij=kijbijpijtijeSij

(2)

式中,kij为调整系数;bij为0,1变量,表示是否进行该环境因素下的可靠性试验;pij表示国家标准对该环境因素下可靠性试验的规定费用水平;tij表示国家标准对该环境因素下的规定试验时间;Sij表示该环境因素下的试验严酷程度;i=1,2,…,n;j=1,2,…,u。

注意,此处讨论的系统可靠性试验费用,仅仅包含与试验相关的费用,不考虑试验样品成本、生产方和消费方损失,以及改进设计过程中的费用。

1.4 试验可靠度提升分析

验前信息能够反映试验前系统的未知参数,包含多来源的信息;由于Beta分布含有两个参数α和β,不同的参数值可以拟合不同形状的分布,文献[2,20-22]指出工程上常常选用Beta分布作为产品各级系统的可靠度验前分布,尤其是成败型产品。Beta分布中包含两个参数α和β,根据概率论相关知识,该分布的均值和方差都可以用该两个参数表示。因此各系统的可靠度验前分布均可表示为π(R|(α,β))的形式。系统的验前分布可由系统自身的历史信息以及仿真信息等渠道得到。

同时,系统可靠度提升与系统可靠性试验的全面程度和严酷程度之间存在一定关系。通过对国内某研究所大量机电类产品试验数据进行拟合发现,Beta分布广泛存在于产品可靠度提升与试验的全面程度Q和严酷程度S之间;又由于可靠性试验的全面程度Q和严酷程度S均在范围[0,1]内,根据文献[23],不失一般性地,设二者与可靠度提升之间存在Beta分布关系。注意,试验的全面程度与严酷程度之间不存在相互影响关系,其为试验的两个考量角度。此外,实际中可靠度的提升不仅仅与可靠性试验所暴露的缺陷有关,还受到维修手段、改进设计等因素的影响。因此本文假定后续改进措施为常量,仅从缺陷暴露的角度考虑可靠度的提升,思路如图2所示。

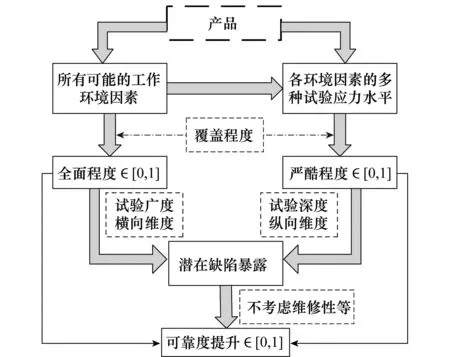
图2 系统可靠度提升思路图Fig.2 System reliability enhancement diagram

设ΔR表示可靠度提升量,Beta分布B(α1,β1)和B(α2,β2)分别表示Q和S带来的系统可靠度提升量,其概率密度函数分别为

(4)

式中,Qi表示第i个子系统的全面程度;Si表示第i个子系统的严酷程度;i=1,2,…,n;α1,β1,α2,β2分别表示该两个Beta分布的参数。

定理1系统的可靠度提升量是全面程度和严酷程度两个变量的联合分布函数,假设Q和S两参数相互独立,则联合分布函数[24]为

(5)

证明根据文献[24],对于系统可靠性试验带来的可靠度提升,从不同侧面描述试验的全面程度Q和严酷程度S两个参数组成了一个二维随机变量 (Q,S);又由于参数Q和S为连续随机变量,二维随机变量(Q,S)的分布可用联合密度函数p(Q,S)给定,但必须满足以下非负性与正则性:

已知Q和S相互独立且分别服从先验Beta分布,则

p(Q,S)=f(Q)·f(S)>0

且

恒成立。

证毕

根据推导出的系统可靠度提升函数关系式,可以建立相关的约束条件,并将可靠度提升最大为目标函数之一进行模型求解,下文将进一步阐述。

2 全面程度和严酷程度测度

2.1 环境因素影响权重

国内外故障统计表明,航空机载设备有52%左右的故障是由环境因素引起的,其中温度因素占42%,振动因素占27%,湿度因素占19%。这3种应力引起的故障占环境因素引起故障的82%左右,因此对各环境因素对产品的可靠性影响是有一定的重要度的,在考虑其对可靠性试验全面程度与严酷程度等参数的影响时,需要考虑各种因素影响的重要程度进行权重设计[18]。

假设某系统工作环境因素有u个,根据相似产品或历史故障统计数据可知,在由该u个环境因素导致的故障中,各环境因素重要程度分别为ω=(ω1,ω2,…,ωu)。其中

ω1+ω2+…+ωu=1

(6)

2.2 全面程度Q

可靠性试验的全面程度实际上就是指试验过程中对系统可能面临的工作环境因素的覆盖程度,文献[19]中以软件的正确性检查条件和测试用例的交叉点为功能点进而定义了功能覆盖率的概念。同理,本文考虑系统(总系统或子系统)的可靠性试验全面程度可用该系统进行试验的环境因素向量与该系统的环境因素影响权重矩阵的乘积来表示。

已知某系统包含n个子系统,且所有可能的试验环境因素共有u个,则如图3所示。

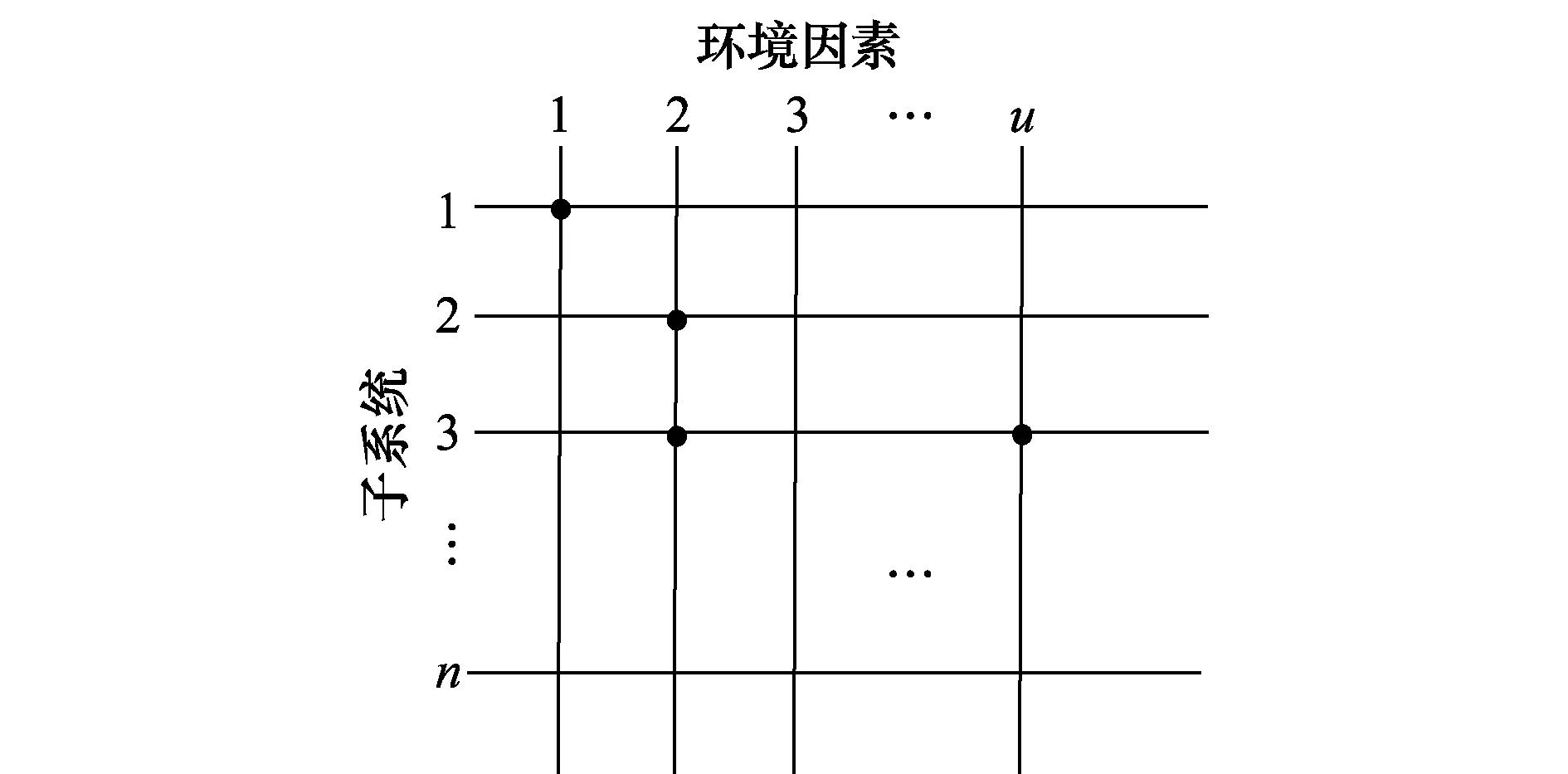
图3 系统-环境因素对应图Fig.3 System-environmental factors corresponding graph

图3的交叉点可作为系统-环境覆盖点,由图3可以得到系统-环境矩阵B:

(7)

式中,bij=0或1;i=1,2,…,n。

因此各子系统的可靠性试验全面程度为

Qi=(bi1,bi2,…,biu)ωT

(8)

由bij=0或1,ω1+ω2+…+ωu=1知,Qi属于[0,1]恒成立。

2.3 严酷程度S

可靠性试验的严酷等级也就是环境应力水平的高低,因此严酷程度S可用试验的应力水平选择来表示。

目前,有许多种不同的术语用来描述系统的各种应力极限[18],如图4所示。

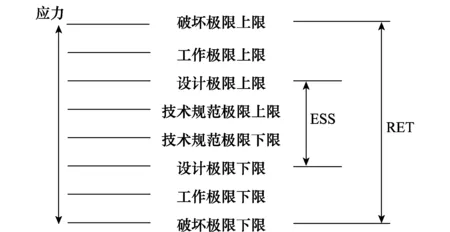
图4 系统的各种应力极限的定义Fig.4 Definitions of various stress limits of the system

在实际的可靠性试验各个环节中,环境应力筛选试验和可靠性强化试验中常采用的应力极限范围如图4所示。可以发现,可靠性试验中的环境应力水平的选择一般是围绕技术规范中心线的范围上下波动,在中心线的两侧均进行一定严酷程度的可靠性试验。

根据严酷程度的定义可知,某环境因素j下的试验严酷程度S为实际试验应力范围对该因素设计极限范围的覆盖程度,可表示为实际应力范围内的应力分布累积密度函数值。

根据经验统计,当某环境因素的应力水平分布服从正态分布时,即

(9)

所以该环境下严酷程度为

(10)

当某环境因素的应力水平分布服从Beta分布时,即

(11)

所以该环境下严酷程度

(12)

式中,Lj0,Uj0为该环境因素设计应力范围的上下界限;Lj,Uj为试验应力范围上下界限，j=1,2,…,u。因为Sj为累积分布函数值,属于[0,1]范围内恒成立。

同时,考虑到环境因素对系统的影响权重,令Zij=bijSij,则某一系统i的可靠性试验严酷程度为

Si=ZijωT

(13)

式中,i=1,2,…,n;j=1,2,…,u;由bij,Sij及ω的取值可知,Si属于[0,1]恒成立。

3 RTDEG模型的建立与求解

3.1 确定目标函数

基于系统潜在缺陷暴露增益定义与可靠性试验费用、可靠度提升假设,以系统的潜在缺陷暴露增益最大和可靠度提升最大为目标,多目标规划模型的目标函数为

(14)

由于潜在缺陷暴露增益表示每单位成本带来的可靠度提升效果,在综合考虑试验资源约束与可靠度提升之间的关系情况下,可认为二者对系统的可靠性试验同等重要。根据文献[25]中所述方法,本文采用线性加权和法将多目标规划问题化为单目标规划问题。

目标函数变为

maxf=0.5f1(Vi)+0.5f2(ΔRi)

(15)

又因为式(14)中,包含了Beta分布f(Qi)和f(Si)的积分运算

(16)

(1-Qi)β1-1dQi·

(17)

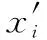
结合式(2)、式(5)、式(8)和式(13)可将参数Qi、Si消去,此时模型中仅包含未知数bij和Sij(i=1,2,…,n;j=1,2,…,u)即

(18)

式中,Zij=bijSij。

3.2 确定约束条件

由定义3、定义4可知,系统可靠性试验的全面程度和严酷程度范围一般为事先约定的范围区间,即

Qi∈[QiU,QiL],Si∈[SiU,SiL]

试验资源的约束,例如成本的限制,则根据式(2)的可靠性试验费用假设,有

式中,C0表示可靠性试验的最大可承受费用。

同时,根据可靠性试验的严酷程度测度方法,各种环境因素下严酷程度均为Sij∈[0,1],因此各环境条件下的应力水平范围为

[Lij,Uij]⊂[Lij0,Uij0]

式中,Lij,Uij分别为该系统i在环境因素j下试验应力范围上下限;Lij0,Uij0分别为系统i在环境因素j下设计应力范围的上下限。

由于试验资源存在一定的约束,无法做到全面程度和严酷程度均达到1的可靠性试验,因此试验的可靠度提升范围为

3.3 构建RTDEG模型

根据确定的目标函数和约束条件,建立RTDEG模型。

(19)

(20)

定理2最优解存在性定理:基于潜在缺陷暴露增益的可靠性试验设计规划模型存在唯一的最优解。

证明由式(19)、式(20)RTDEG模型可知,若存在bij、Sij,使得该单目标函数取得唯一的最小值或最大值,则该RTDEG模型存在唯一的一组解。又因为bij为0,1变量,若优化模型存在最优解,不影响可行域的范围。因此,只需证明对于∀Sij∈D时RTDEG模型是一个凸集上的凸规划问题即可,其中D为定义域。

首先,判断目标函数是凹函数或凸函数,考虑变量Sij时目标函数f的海赛矩阵为

(21)

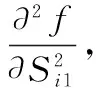
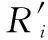
(1-(bi1ωT))β1-1d(bi1ωT)>0

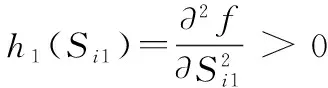
因此,可知目标函数f为一个凸函数,而约束条件均为线性约束条件,该RTDEG模型为一个凸集上的凸规划问题,在可行域上必定存在唯一的最优解。

证毕

利用模型求解后,得到系统i在环境因素j下的可靠性试验严酷程度Sij(Sij∈[0,1]),结合式(9)～式(12),有

(22)

或

(23)

由于正态分布或Beta分布均为已知,在满足严酷程度Sij的基础上的各环境因素应力水平的范围[Lij,Uij]均可作为实际试验应力范围。

4 案例分析

中国商飞美国公司与某高校联合开发了一种新型可脱离的飞机机载设备——“报信者”系统,主要实现飞机飞行状态监测以及飞机事故记录等功能。该系统主要包含智能触发系统、设备弹射系统、跟踪记录系统以及设备定位与回收系统4个子系统,各子系统为简单串联结构关系。图5为报信者系统的产品总体结构逻辑框图。

图5 报信者系统总体结构逻辑框图Fig.5 Overall structure logic diagram of the Harbinger system

智能触发系统结构如图6所示。由于该系统为飞机机载设备,其一般工作环境可视为与飞机相近。经过对其典型工作环境要素进行分析,可确定5类环境因素,分别为温度(℃)、湿度(%RH)、振动(Hz)、砂尘(g/m3)以及压强(kPa)。根据设备使用数据以及相近产品历史统计数据,成立专家小组经过调研讨论后得出各环境因素对产品故障的影响程度分别为ω1=19%、ω2=23%、ω3=39%、ω4=14%和ω5=5%。

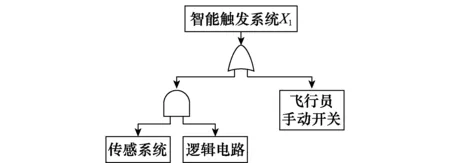
图6 报信者智能触发系统结构图Fig.6 Structure of the intelligent trigger system of the Harbinger

经过对实际工作环境以及试验前信息的分析,确定了智能触发系统的部分参数,如表1所示。

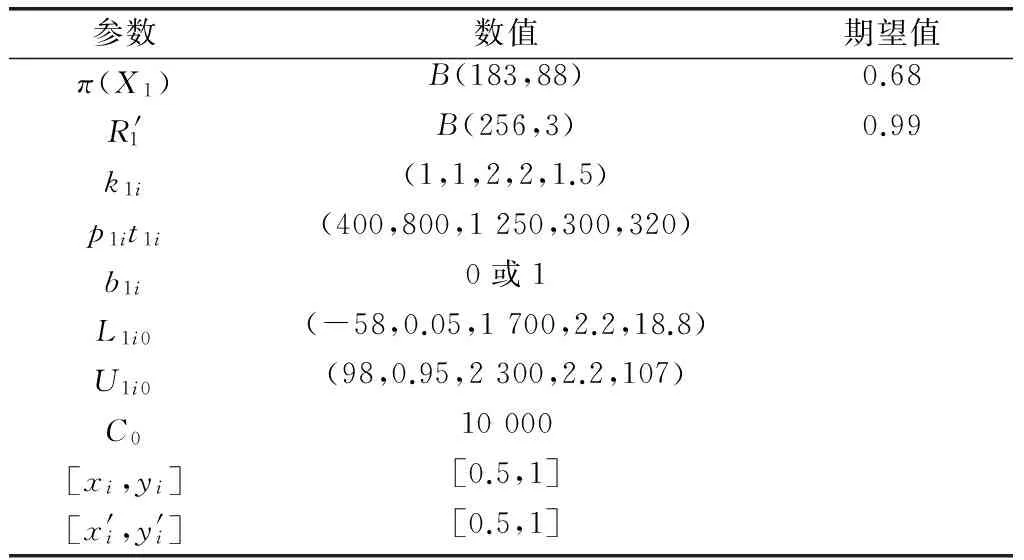
表1 参数赋值说明

该系统可能工作环境(即试验范围)的温度范围为-58～98 ℃,振动频率的范围为1 700～ 2 300 Hz,根据正态分布的三西格玛原理,其可用正态分布分别表示为

S11～N(20,262),S13～N(2000,1002)

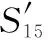
图7 湿度因素严酷程度分布函数图像Fig.7 Humidity factor severity distribution function image

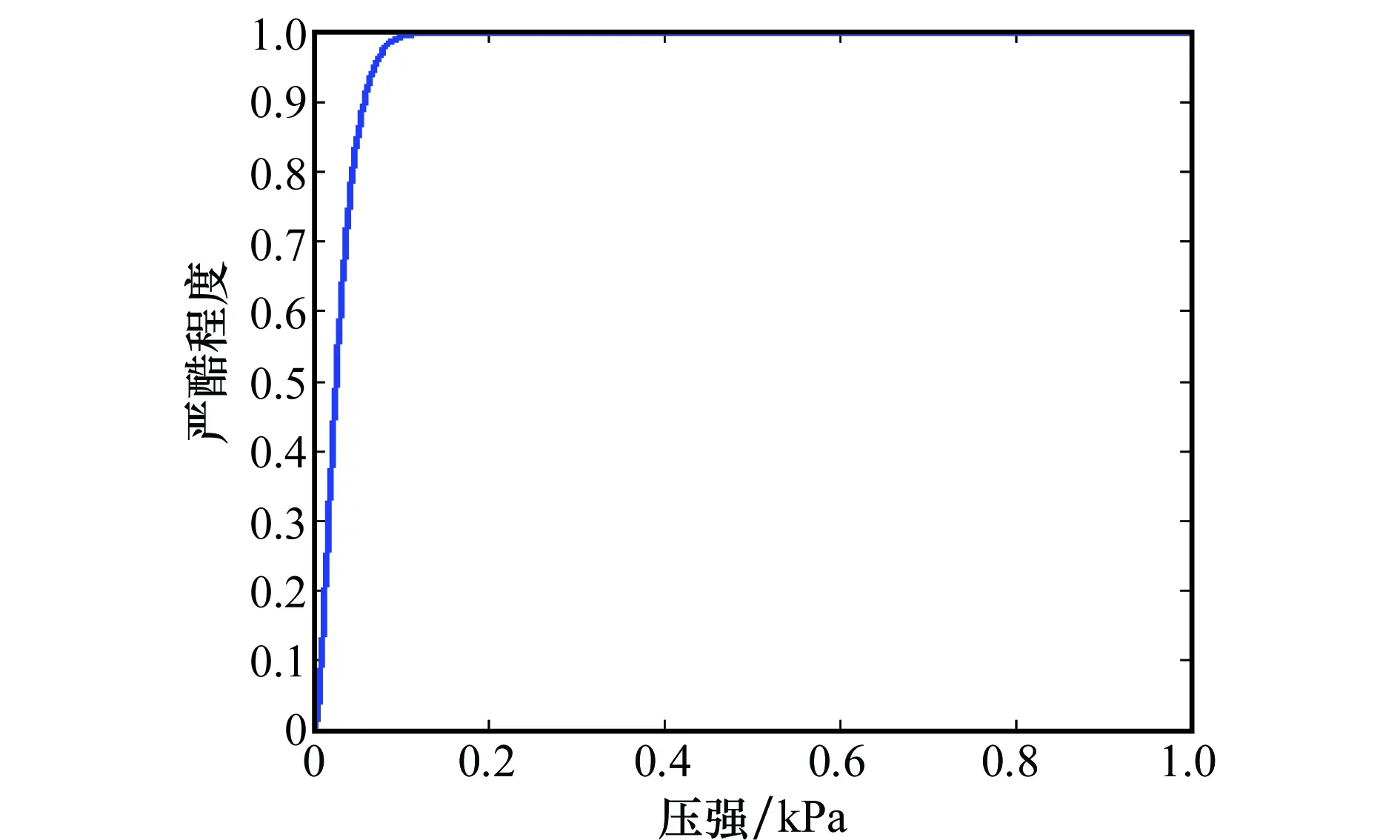
图8 压强因素严酷程度分布函数图像Fig.8 Pressure factor severity distribution function image

由图7、图8可知,湿度因素的严酷程度随着湿度水平的提升逐渐增加;压强因素的严酷程度在横轴为0.1附近,逆归一化后得出当压强在20 kPa左右时其严酷水平即可达到1左右。

注意到砂尘因素在此处为固定值,因此该因素的严酷程度为S14=1。

针对智能触发系统的试验全面程度和严酷程度,其与可靠度提升之间的Beta分布关系为

(24)

式中,f(Q1)～B(2,2),f(S1)～B(3,3)。

根据第3节的模型求解方法,将表1中参数代入到RTDEG模型中,利用Matlab软件求解得出参数结果，如表2所示。

表2 计算结果

由表2中参数结果可知,针对该智能触发系统,若对其进行可靠性试验,在费用约束为10 000元的前提下,需对温度、湿度、振动、砂尘4种环境因素进行试验,且温度、湿度和砂尘3种因素需按照设计极限进行可靠性试验,振动环境下的可靠性试验严酷程度为0.714 3即可。此时智能触发系统的潜在缺陷暴露增益最大为0.000 029 78,系统试验的全面程度为0.95,严酷程度为0.838 6,此情况下的系统试验后的预期可靠度提升量为0.297 7,接近于系统期望值0.31。由此可以针对该智能触发系统进行可靠性试验的设计规划,对该子系统应该进行哪些可靠性试验、所进行的试验的应力水平范围均可进行预先设计,验证了模型的有效性。

限于篇幅,本文仅针对报信者系统中的智能触发系统进行了可靠性试验的设计规划,但本文提出的模型是普遍适用的。将模型中的参数改为其他各级系统的参数后,可以类比进行计算,得出设备弹射系统、跟踪记录系统、设备定位与回收系统或者逻辑电路子系统、飞行员手动开关子系统以及集成度较高的整体系统的可靠性试验设计规划参数,指导该报信者设备各级系统的可靠性试验,还可拓展至其他设备领域。

5 结 论

针对可靠性试验设计规划的研究目前较少,因此本文从可靠性试验执行者的角度,在试验未开始时,对待试验系统应该进行哪些试验、试验需要进行到什么程度进行了分析讨论,主要工作如下:

(1) 提出了系统潜在缺陷暴露增益的概念,阐述了增益即试验所花成本对系统的可靠度提升的效果;

(2) 从可靠性试验的全面程度和严酷程度两个角度出发,分析了这两个参数与系统的试验费用和可靠度提升量之间的关系,并构建了基于Beta分布的函数模型,进一步进行RTDEG模型的构建;

(3) 综合考虑每种环境因素与系统可靠性试验导致的可靠度提升之间的关系,提出了一种基于系统RTDEG模型,在试验资源约束(一般为成本约束)存在的情况下,对系统的可靠性试验进行设计规划,得出应该进行的试验类型和应力水平范围。

本文的研究还可扩展至复杂装备系统的可靠性试验中,尤其是在当前主制造商-供应商模式下,可指导各级供应商对自身提供的产品进行可靠性试验的设计规划,从而针对性地进行试验。同时,在各级供应商得出相应的全面程度和严酷程度的数据的基础上,采用一定的技术手段对其进行融合处理,以便主制造商可以有效利用数据,进一步减小可靠性试验成本是需要进一步研究的问题。

参考文献：

[1] 冯文哲, 刘琦. 基于试验损失的指数型产品Bayes可靠性试验设计[J]. 系统工程学报, 2012, 27(4): 568-574.

FENG W Z, LIU Q. Bayes reliability experimental design for exponential distributed product based on experimental loss[J]. Journal of Systems Engineering, 2012, 27(4): 568-574.

[2] 张安扬,刘琦.基于信息融合的系统可靠性优化试验设计模型[J].航空动力学报,2016,31(2):330-336.

ZHANG A Y, LIU Q. Optimization reliability test design modeling based on information fusion[J]. Journal of Aerospace Power, 2016, 31(2): 330-336.

[3] 杨兆军,陈传海,陈菲,等.数控机床可靠性技术的研究进展[J].机械工程学报,2013,49(20): 130-139.

YANG Z J, CHEN C H, CHEN F, et al. Progress in the research of reliability technology of machine tools[J]. Journal of Mechanical Engineering, 2013, 49(20): 130-139.

[4] MENG L, BU W. The reliability design and performance tested technology of high speed and precision CNC machine tool[J]. Wireless Internet Technology, 2015(21): 142-144.

[5] 李洪洲, 杨兆军, 许彬彬, 等. 数控机床可靠性评估试验周期设计[J]. 吉林大学学报(工学版), 2016, 46(5): 1520-1527.

LI H Z, YANG Z J, XU B B, et al. Design of testing period for reliability assessment of NC machine tools[J]. Journal of Jilin University(Engineering and Technology Edition),2016,46(5): 1520-1527.

[6] 马蕾, 何成刚, 赵相吉, 等. 低温环境下轮轨材料滚动磨损模拟试验研究[J]. 摩擦学学报, 2016, 36(1): 92-97.

MA L, HE C G, ZHAO X J, et al. Simulation experiment for rolling wear of wheel/rail materials under low temperature environment[J]. Tribology, 2016, 36(1): 92-97.

[7] YE Z S, CHEN N. The inverse Gaussian process as a degradation model[J]. Technometrics, 2014, 56(3): 302-311.

[8] 李烁, 陈震, 潘尔顺. 广义逆高斯过程的步进应力加速退化试验设计[J]. 上海交通大学学报, 2017, 51(2): 186-192.

LI S, CHEN Z, PAN E S. Step-stress accelerated degradation test plan for generalized inverse Gaussian process[J]. Journal of Shanghai Jiaotong University, 2017, 51(2): 186-192.

[9] YANG G B. Optimum constant-stress accelerated life-test plans[J]. IEEE Trans.on Reliability, 1994, 43(4): 575-581.

[10] TANG L C, TAN A P, ONG S H. Planning accelerated life tests with three constant stress levels[J]. Computers & Industrial Engineering, 2002, 42(2): 439-446.

[11] SHEN G Y, MIAO J, SHAO J W. Research on accelerated life test system for water quality analyzer[J]. Applied Mechanics & Materials, 2014, 635-637.

[12] CAI M, YANG D, TIAN K, et al. Step-stress accelerated testing of high-power LED lamps based on subsystem isolation method[J]. Microelectronics Reliability, 2015, 55(9/10): 1784-1789.

[13] HEONSANG L, BONGJIN Y. Optimal design of accelerated degradation tests based on Wiener process models[J]. Journal of Applied Statistics, 2011, 38(2): 309-325.

[14] HU C H, LEE M Y, TANG J. Optimum step-stress accele-rated degradation test for Wiener degradation process under constraints[J]. European Journal of Operational Research, 2015, 241(2): 412-421.

[15] 张伟. 温、湿、振三综合环境试验技术的应用[J]. 电子产品可靠性与环境试验, 2004(6):38-41.

ZHANG W. Integrated environmental test of temperature, humidity and vibration[J]. Electronic Product Reliability and Environmental Testing, 2004(6): 38-41.

[16] 方兵, 沈润杰, 何闻, 等. 航天器元件多参数综合可靠性环境试验研究综述[J]. 中国机械工程, 2009(22): 2766-2771.

FANG B, SHEN R J, HE W, et al. Research summary of the multi-parameter combined environmental test of spacecraft component reliability[J].China Mechanical Engineering,2009(22):2766-2771.

[17] 陈循, 温熙森. 环境试验技术的现状综述与集成环境应力试验分析系统[J]. 国防科技大学学报, 1998(6):81-85.

CHEN X, WEN X S. The situation summarization of environment experiment technology and integration environment stress experiment & analysis system[J]. Journal of national University of Defense Technology, 1998(6): 81-85.

[18] 姜同敏, 王晓红, 袁宏杰, 等.可靠性试验技术[M]. 北京: 北京航空航天大学出版社, 2012: 8-117.

JIANG T M, WANG X H, YUAN H J, et al. Reliability test technique[M]. Beijing: Beihang University Press, 2012:8-117.

[19] 迟志刚, 高德远, 樊晓桠, 等. 一种基于功能覆盖率的验证环境的构建方法[J]. 计算机工程与应用, 2006, 42(5): 88-90.

CHI Z G, GAO D Y, FAN X Y, et al. A coverage-driven method to construct verification environment[J]. Computer Engineering and Applications, 2006, 42(5): 88-90.

[20] 李学京.置信分布的贝塔分布近似及其在可靠性统计中的应用[J].强度与环境, 2007, 34(2): 17-23.

LI X J. Beta distribution approximation of confidence distributions and application in reliability statistics[J]. Structure & Environment Engineering, 2007, 34(2): 17-23.

[21] 明志茂, 陶俊勇, 陈循, 等. 基于混合Beta分布的成败型产品Bayes可靠性鉴定试验方案研究[J]. 兵工学报, 2008, 29(2): 204-207.

MING Z M, TAO J Y, CHEN X, et al. A Bayes plan of reliability qualification test based on the mixed beta distribution for success/failure product[J]. Acta Armamentarii, 2008, 29(2): 204-207.

[22] 冯志刚,李静,高普云,等.贝塔分布在数据转换中的应用及其优化分布参数确定[J].机械强度,2011,33(4): 554-557.

FENG Z G, LI J, GAO P Y, et al. Application of Beta distribution in data convert and its optimize parameter ascertain.[J]. Journal of Mechanical Strength, 2011, 33(4): 554-557.

[23] 胡尧, 卢大远. 变环境条件下型号设备的可靠性估计[J]. 统计与决策, 2011(6): 32-34.

HU Y, LU D Y. Reliability estimation of model equipment under variable environment conditions[J]. Statistics and Decision, 2011(6): 32-34.

[24] MIZ M L G, KULASEKERA K B, LIMNIOS N, et al. Applied Nonparametric Statistics in Reliability[M]. Boston: Houghton Mifflin, 2011: 93-96.

[25] BAKY I A. Solving multi-level multi-objective linear programming problems through fuzzy goal programming approach[J]. Applied Mathematical Modelling, 2010, 34(9): 2377-2387.