基于稀疏恢复谱相似度的自适应样本筛选算法

王晓明, 李 军, 张圣鹋, 卢 燕, 张永杰

(1. 电子科技大学电子工程学院, 四川 成都 611731;2. 毫米波遥感技术重点实验室, 北京 100854)

0 引 言

机载雷达的空时自适应处理(space-time adaptive processing,STAP)技术采用协方差矩阵计算最优权[1],经典的滑窗(sliding window,SW)法利用待检测单元(cell under test,CUT)两侧的样本对协方差矩阵进行最大似然估计[2]。而在实际工作中,机载雷达面临的环境通常是非均匀的,复杂的地形(水陆交界、城市区域等)以及训练样本中包含动目标(交通网上的车辆等)均将导致用于估计杂波背景的参考单元样本难以满足独立同分布要求,从而造成STAP性能下降[3-4]。因此在非均匀杂波环境下,需剔除被干扰目标污染的样本,筛选得到与CUT样本杂波统计特性相似的样本(认为是均匀样本)以提升杂波协方差矩阵的估计性能。

已有的样本筛选算法主要有基于高程数据、地形信息等先验知识的筛选算法[5-6]以及基于回波数据的自适应筛选算法两类。对于利用先验知识的筛选算法,其性能依赖于先验知识的准确程度以及配准精度,而先验信息的不准确可能会导致算法性能恶化[7]。故本文重点研究基于回波数据的样本筛选算法。

在不依赖先验信息前提下,广义内积(generalized inner product,GIP)算法广泛应用于样本筛选中[8]。然而,当杂波环境非均匀性较强(即参考单元样本中多数为非均匀样本)时,用于筛选判决依据的杂波协方差矩阵统计量将不能被准确估计,导致筛选出的样本主要为非均匀样本,不满足与CUT样本的独立同分布条件。文献[9]通过改进对污染样本与参考单元样本差异的度量,相比GIP算法获得了更高的污染样本辨别能力。文献[10]将GIP算法与扁长椭球波函数结合,通过迭代方法提高了样本筛选性能。然而,这些改进算法均未利用CUT的信息,对于较强的非均匀杂波场景,鲁棒性不足。

文献[11]提出的基于傅里叶谱相似度(Fourier spectrum similarity,FSPS)的样本筛选算法,直接对比参考单元与CUT傅里叶谱的相似程度实现样本的筛选,解决了筛选算法在非均匀杂波场景下的鲁棒性问题。该算法不受杂波环境非均匀程度的影响,在杂波环境非均匀性较强时有明显优势。然而,FSPS算法中用于筛选判决依据的傅里叶谱,其分辨率正比于系统自由度,导致FSPS算法在系统自由度较小的情况下无法进行有效筛选。

针对FSPS算法在小系统自由度场景下分辨率不足的问题,本文提出一种基于稀疏恢复谱相似度的样本筛选算法。该方法采用超分辨稀疏重构技术[12-13],对CUT样本与参考单元样本进行高分辨率的谱恢复,利用恢复谱进行污染样本的剔除以及均匀样本的自适应筛选,相对于FSPS算法有更高的非均匀样本分辨精度。仿真结果表明,所提方法在非均匀杂波场景下具有一定鲁棒性,并在较小系统自由度情况下展现出优于FSPS算法的样本筛选能力及全局输出性能。

1 信号模型及问题描述

考虑工作于正侧视模式的N阵元均匀线阵机载相控阵雷达。载机速度为v,脉冲重复周期为Tr,工作波长为λ,阵元间距为d。设一个相干处理间隔(coherent processing interval,CPI)内每个阵元接收脉冲数为K,则CUT单元的雷达接收回波数据可采用二元假设检验表示为

(1)

式中,α为目标信号复幅度;Θ(ft,θt)∈CNK×1为目标信号空时导向矢量;ft、θt为目标归一化多普勒频率、目标归一化空间频率;xc为杂波回波数据矢量;n为噪声矢量。

STAP滤波器的空时最优权[14]为

wopt=μR-1Θ

(2)

FSPS算法分为两步,第一步利用相关系数对污染样本进行剔除。参考单元样本l与目标导向矢量的相关系数ρl定义为

(3)

式中,‖·‖F表示Frobenius范数。ρl越大,xl含有目标的可能性越大。计算每个参考单元样本的相关系数ρl,去掉ρl值较大的样本,剩余的样本继续用于后续筛选。

第二步通过比较CUT与参考单元样本的傅里叶谱,进行相似样本选择。首先对待筛选样本及CUT样本分别计算空时二维傅里叶谱。分别将归一化空间频率、归一化多普勒频率均匀划分为N、K份。设ηkn,l和ηkn,cut分别表示第l个参考单元样本和CUT样本的傅里叶谱在(fk,θn)处的值,则第l个参考单元样本与CUT样本的谱相似度系数gl由式(4)计算。

(4)

式中,k=1,2,…,K;n=1,2,…,N;k,n∉Ω，其中Ω为目标通道保护单元。认为有较小gl值的样本与CUT具有相近的杂波特性,这些样本将被保留下来用作R的估计。

FSPS算法的优势在于将CUT单元的杂波特性直接用于样本筛选,筛选性能不受杂波非均匀程度的影响。然而,当系统自由度较低时,该算法的筛选效果并不理想,原因在于FSPS算法的筛选性能完全依赖于傅里叶谱对杂波特性的反应程度,而空时二维傅里叶谱的分辨率取决于阵元数与脉冲数。在系统自由度较低的情况下,傅里叶谱的分辨率也较低,导致FSPS算法在第一步中无法有效剔除被干扰目标污染的样本,出于同样的原因，在第二步的谱相似度比较中也不能很好地分辨出非均匀样本与均匀样本的差异。而STAP滤波器是高分辨的滤波器,因此FSPS算法的低分辨率问题将直接导致STAP滤波器输出性能的损失。

针对这一问题,第2节将给出了一种利用稀疏恢复技术的样本筛选算法,该算法在系统自由度较小的场景下具有优于FSPS算法的样本筛选能力。

2 基于稀疏恢复谱相似度的样本筛选算法

杂波环境非均匀程度较强时,传统的基于回波数据统计特性的样本筛选算法性能会严重下降。为增强筛选算法在非均匀环境下的鲁棒性,应直接提取CUT与每个参考单元的杂波特征信息进行对比,从而筛选出均匀样本。机载雷达杂波谱的稀疏性[15-16]及稀疏恢复技术的发展[17-18]使对单个样本恢复出高分辨率杂波谱成为可能。本节给出一种基于稀疏恢复谱相似度(sparse recovery spectrum similarity,SR-SPS)的参考单元样本筛选算法。

2.1 稀疏恢复谱算法原理

如第1节所述,由于傅里叶谱的分辨精度由阵元脉冲数决定,FSPS算法的筛选性能受系统自由度的影响。与之不同,稀疏恢复技术恢复出的空时功率谱的精度可由空时字典精度决定。将归一化多普勒频率和归一化空间频率均匀地分成Nd,Ns份,其中Nd=ρK,Ns=ρN,ρ为恢复尺度,通常可取ρ为4～10的整数[19]。频点(fj,θi)(j=1,2,…,Nd;i=1,2,…,Ns)处的导向矢量可表示为φ(fj,θi)∈CNK×1。在允许一定量化误差的情况下,目标导向矢量Θ(ft,θt)可表示为φ(fjt,θit),即目标位于第jt个多普勒频率通道,第it个空间频率通道。任意空时回波快拍信号x∈CNK×1可表示为

(5)

式中,矩阵Φ=[φ(f1,θ1),φ(f1,θ2),…,φ(fNd,θNs)]为NK×NdNs维空时导向字典(超完备基);γ= [γ1,1,γ1,2,…,γNd,Ns]T∈CNdNs×1代表x在角度-多普勒域(由空时导向字典Φ表示)上的复幅度,也可称为角度-多普勒像(angle-Doppler profile,A-DP)[12]。则回波信号x的稀疏恢复空时功率谱为

α=reshape(E[γ⊙γ*],Nd,Ns)

(6)

式中,reshape(A,m,n)表示将向量A转化为m行n列的矩阵;⊙表示Hadamard积;(·)*表示共轭。对于γ的求解,文献[19]给出了一种用加权L1范数代替传统L0范数的求解式,即

(7)

式中,κ为正则化参数;矩阵W除对角线元素外,其他元素取值均为零。

(8)

式中,j=1,2,…,Nd;i=1,2,…,Ns。

L1范数加权优化问题可以利用CVX Matlab工具箱中的函数求解。

2.2 SR-SPS样本筛选算法

稀疏恢复得到的A-DP作为回波样本数据的一个特征量,反应各距离单元(距离门)回波信号在不同空时通道的能量水平,包含了各距离单元回波信号的高分辨率特征信息。以之作为不同样本间的相似度评估依据,较傅里叶谱而言更符合高分辨率的STAP滤波器对样本筛选算法的要求。因此,本文以对比A-DP相似程度为依据,提出SR-SPS的样本筛选算法。

SR-SPS算法的基本思想为,利用CUT以及参考单元样本的稀疏恢复谱对参考单元样本进行两步筛选。首先从初始参考单元样本集0中剔除可能被干扰目标污染的样本,得到样本集1;然后从1中筛选出与CUT单元稀疏谱相似度较高的样本作为训练样本,用于R的估计。具体步骤如下。

步骤1高精度谱的稀疏恢复

由式(7)和式(8)得到CUT单元的A-DP为

(9)

(10)

由于稀疏恢复所得A-DP中,目标能量可能泄露到邻近的角度-多普勒单元,因此需设置目标保护区域Λ,对期望目标所在空时通道进行扩展。目标保护区域内的空时通道均可能包含目标信号成分。保护区域Λ内的空时通道集的计算式为

(11)

图1为经稀疏恢复得到的CUT与初始参考单元样本的A-DP矩阵示意图。其中L0、L1分别为集合0、1中的元素个数,黑色矩形区域为目标保护区域Λ。

图1 雷达回波空时像矩阵示意图Fig.1 Sketch map of radar echo space-time profile matrix

步骤2剔除被污染的参考单元样本

为防止选择出的训练样本中含有被干扰目标污染的样本导致滤波环节出现目标自相消[7],在选择相似样本前应先去除这些被污染的样本。

(12)

则ηl0值较大的样本被干扰目标信号污染的可能性较大,应予以剔除。此步筛选过程如图1中第①步所示,筛选后得到样本集1。

步骤3杂波特性相似样本选择

(13)

综上,所提算法的流程框图如图2所示。

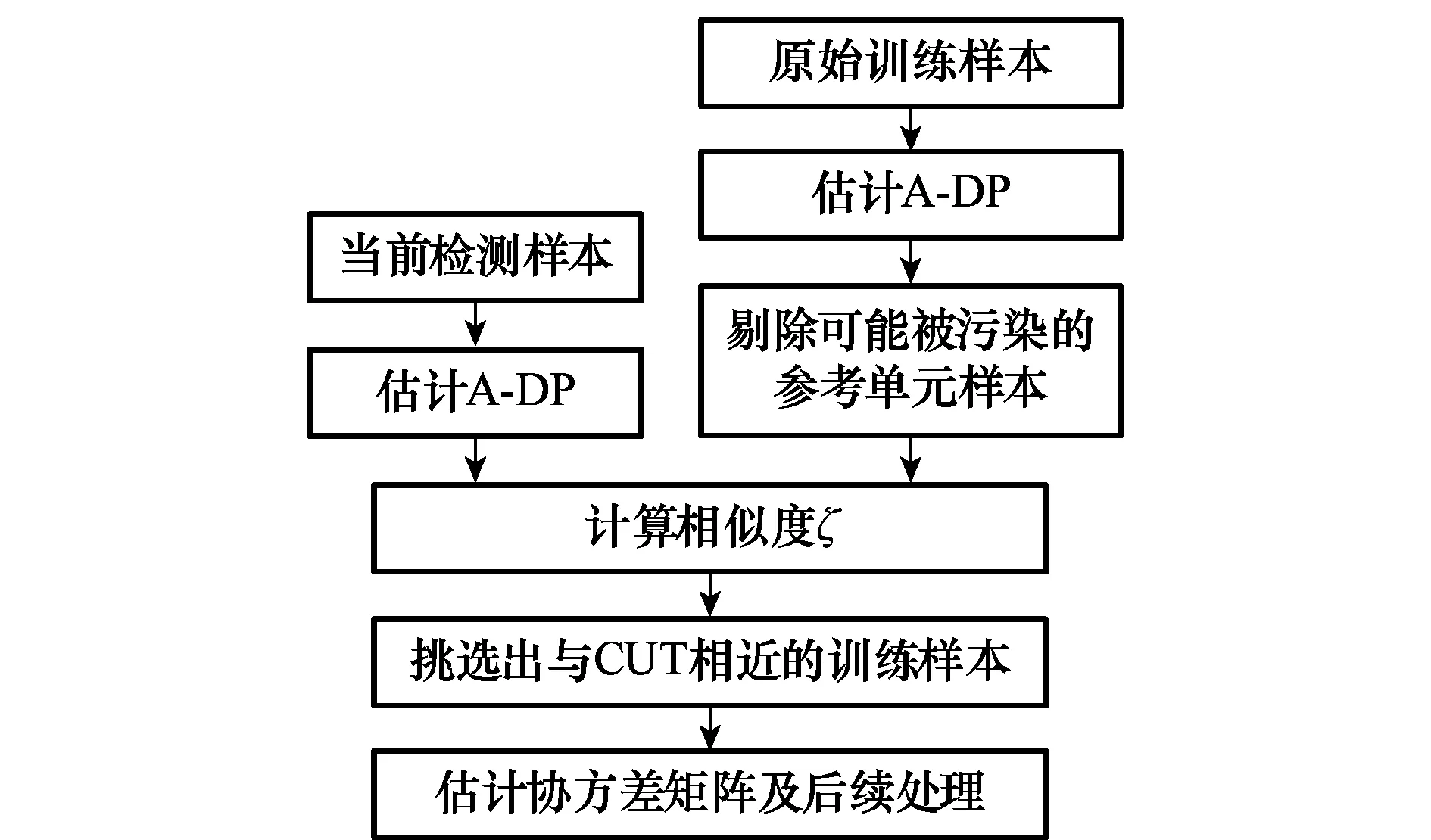
图2 所提算法流程图Fig.2 Flowchart of the proposed method

需指出的是,文献[20]所提方法是利用稀疏恢复得到的角度-距离谱来剔除被目标信号污染的样本,取得较好的效果。但此算法并没有利用CUT单元信息从非均匀杂波的参考单元样本中筛选出均匀样本。本文所提方法在剔除污染样本的同时,利用CUT恢复出的高精度谱筛选出接近CUT杂波特性的训练样本,使STAP输出性能得到进一步提升。

3 仿真结果

本节将通过计算机仿真来验证所提算法的有效性。仿真参数设置如下。

工作于正侧视的均匀线阵机载相控阵雷达,阵元个数N=8、脉冲个数K=8;d=λ/2;杂波折叠系数β=2v·Tr/d=1;目标的归一化空间频率为0;信噪比(signal-to-noise ratio, SNR)为0 dB。构造由两种地形组成的非均匀杂波区域:其中区域A的信号杂波噪声比(signal-to-clutter-noise ratio, SCNR)为25 dB,脉冲间起伏系数采用预处理后的IPIX实测数据构造[21],预处理低通滤波器通带频率参数为ωp=0.02、阻带频率参数为ωs=0.006;区域B的SCNR为30 dB,谱宽通带频率参数为ωp=0.06、阻带频率参数为ωs=0.01。设CUT单元位于区域A,则区域A称为均匀杂波区,其内样本为均匀样本;区域B称为非均匀杂波区,其内样本为非均匀样本。另设区域A中的参考单元样本J存在归一化空间频率为0,归一化多普勒频率为-0.28的干扰目标信号。干噪比(jammer-to-noise ratio, JNR)为5 dB。考虑到计算量问题,仿真实验取恢复尺度ρ=4。

STAP滤波器的输出性能由输出SCNR损失由LSCNR给出,即

(14)

样本J(含干扰目标信号)的傅里叶谱如图3(a)所示,稀疏恢复功率谱如图4(a)所示;非均匀样本的傅里叶谱如图3(b)所示,稀疏恢复功率谱如图4(b)所示。

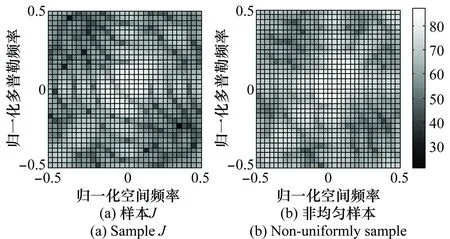
图3 傅里叶空时功率谱Fig.3 Fourier space-time power spectrum

图4 稀疏恢复空时功率谱Fig.4 Sparse recovery space-time power spectrum

由图3可知,傅里叶空时功率谱的分辨率较低,无法分辨出是否存在干扰目标信号。原因在于傅里叶谱中有大量的杂波能量泄露到干扰目标所在位置。由图4可知,稀疏恢复得到的空时功率谱具有较高的分辨率,相比传统快速傅里叶变换(fast Fourier transform, FFT)方法能获得突破瑞利分辨极限的分辨能力,可较清晰地分辨出干扰目标和非均匀样本的谱展宽。

下面给出FSPS算法与本文所提SR-SPS算法的样本筛选结果对比。共有96个待筛选参考单元样本,编号1～48的距离单元位于上述均匀杂波区域A,并包含样本J;编号49～96的距离单元位于上述非均匀杂波区域B。各筛选算法将从参考单元样本中选出40个样本用于R的估计。

FSPS算法以及本文所提SR-SPS算法的筛选结果如图5所示。图5(a)中蓝色实线为FSPS算法的相似度系数gl;图5(b)中蓝色实线为SR-SPS算法的相似度系数ζl1;红色星号为各算法选择出的样本单元。

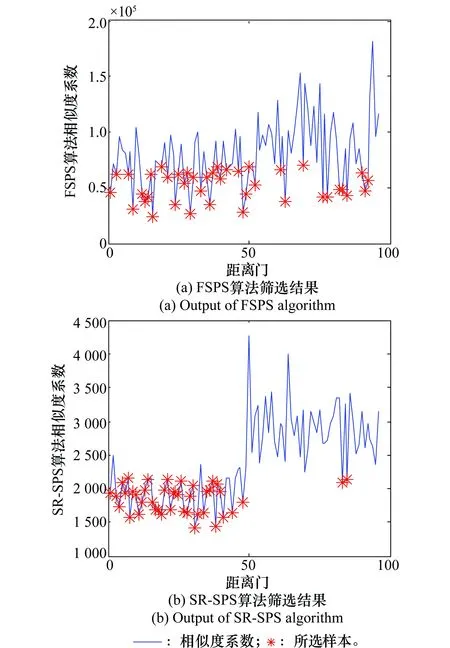
图5 不同算法的筛选结果对比Fig.5 Output of both selection algorithm

由图5可以看出,SR-SPS算法选择出的样本基本处于与CUT杂波特性相似的均匀区,而FSPS算法筛选出的样本则包含了较多的非均匀样本。

图6给出了该场景下,分别采用SR-SPS算法、FSPS算法、GIP算法、以及仅采用SW算法进行参考单元样本筛选,共4种情况下的LSCNR曲线。图6所示结果表明,在仿真实验讨论的杂波非均匀性较强且雷达系统自由度较低的场景下,本文提出的SR-SPS算法相对于GIP算法以及文献[11]提出的FSPS算法均具有更优的全局输出性能。

图6 输出SCNR损失曲线Fig.6 SCNR loss

为进一步说明所提SR-SPS算法在系统自由度较小场景下的性能优势,图7给出了不同样本筛选算法的LSCNR随系统自由度变化的曲线。具体仿真参数设置如下:阵元个数N=4,8,12,16,20,30，脉冲个数K=N;目标的归一化空间频率为0，归一化多普勒频率为-0.1;SNR=0 dB;待筛选参考单元样本一半位于区域A,一半位于非均匀区域B(可视为较严重的非均匀场景)。除系统自由度为900时,分辨尺度ρ′=2外,其他系统自由度情况下ρ=4。

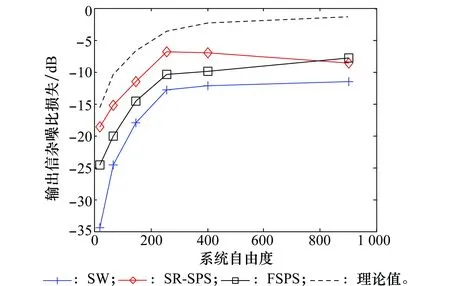
图7 不同系统自由度下的输出SCNR损失曲线Fig.7 SCNR loss against different systems’ degrees of freedom

图7所示结果表明,在系统自由度较低时,SR-SPS算法相对FSPS算法具有明显优势。随着系统自由度增大,两种算法性能逐渐趋于相似,均优于传统的SW算法。因此,SR-SPS算法的优势主要体现在低系统自由度的场景。

另需说明的是,SR-SPS算法恢复出的功率谱精度取决于空时导向字典精度,高精度的谱恢复是以高计算量为代价的。仿真实验出于计算量的考虑,在系统自由度为900时降低了恢复精度(ρ′=2),因此恢复性能略有损失。但由图7可知,在系统自由度为900的条件下,SR-SPS算法与FSPS算法相比,LSCNR的恶化小于1 dB,仍得到了较好的筛选性能。

4 结 论

本文所提SR-SPS样本筛选算法通过稀疏恢复得到的高精度谱来剔除可能被干扰目标污染的样本,同时根据CUT与参考单元稀疏恢复高精度谱的相似度筛选出接近CUT杂波特征的样本,改善了FSPS算法在筛选过程中分辨率不足的问题。仿真结果表明,所提SR-SPS算法保留了FSPS算法在非均匀杂波场景下具有一定的鲁棒性,同时提升了对非均匀杂波样本的分辨能力,获得了良好的样本筛选效果。

参考文献：

[1] HERBERT G M. Clutter modelling for space-time adaptive processing in airborne radar[J]. IET Radar, Sonar & Navigation, 2010, 4(2): 178-186.

[2] WU J X. Sliding window recursive QR factorization of space-time adaptive processing algorithm[J]. Journal of Electronics & Information Technology, 2011, 30(10): 2338-2342.

[3] DAI B, WANG T, WU J, et al. Adaptively iterative weighting covariance matrix estimation for airborne radar clutter suppression[J]. Signal Processing, 2015, 106(C): 282-293.

[4] WANG Z, WANG Y,DUAN K,et al.Subspace-augmented clutter suppression technique for STAP radar[J]. IEEE Geoscience & Remote Sensing Letters, 2016, 13(3): 462-466.

[5] TANG B,ZHANG Y,TANG J,et al.Close form maximum likelihood covariance matrix estimation under a knowledge-aided constraint[J]. IET Radar, Sonar & Navigation, 2013, 7(7): 904-913.

[6] BLUNT S D, GERLACH K, RANGASWAMY M. Stap using knowledge-aided covariance estimation and the fracta algorithm[J]. IEEE Trans.on Aerospace & Electronic Systems, 2006, 42(3): 1043-1057.

[7] 吴亿锋, 王彤, 吴建新,等. 基于道路信息的知识辅助空时自适应处理[J]. 电子与信息学报, 2015,37(3): 613-618.

WU Y F, WANG T, WU J X, et al. A knowledge aided space time adaptive processing based on road network data[J].Journal of Electronics & Information Technology,2015,37(3):613-618.

[8] RABIDEAU D J, STEINHARDT A. Improved adaptive clutter cancellation through data-adaptive training[J]. IEEE Trans.on Aerospace & Electronic Systems, 1999, 35(3): 879-891.

[9] 王强, 张永顺, 刘汉伟,等. 基于矩阵相似度的空时二维干扰检测方法[J]. 系统工程与电子技术, 2017, 39(2): 259-262.

WANG Q, ZHANG Y S, LIU H W, et al. Interference detecting method for space-time two-dimension based on matrix similarity[J]. Systems Engineering and Electronics, 2017, 39(2): 259-262.

[10] DU W, LIAO G, YANG Z. Robust space time processing based on bi-iterative scheme of secondary data selection and PSWF method[J].Digital Signal Processing,2016,52(C):64-71.

[11] WU Y, WANG T, WU J, et al. Robust training samples selection algorithm based on spectral similarity for space-time adaptive processing in heterogeneous interference environments[J]. IET Radar, Sonar & Navigation, 2015, 9(7): 778-782.

[12] SELESNICK I W, PILLAI S U, LI K Y, et al. Angle-Doppler processing using sparse regularization[C]∥Proc.of the IEEE International Conference on Acoustics,2010:2750-2753

[13] YANG Z. Direct data domain sparsity-based STAP utilizing subaperture smoothing techniques[J]. International Journal of Antennas & Propagation, 2014, 2014(1): 1-10.

[14] WARD J. Space-time adaptive processing for airborne radar[J]. Space-Time Adaptive Processing, 1998, 5(241): 2/1-2/6.

[15] SUN K, ZHANG H, LI G, et al. A novel STAP algorithm using sparse recovery technique[C]∥Proc.of the IEEE International Geoscience and Remote Sensing Symposium, 2009:336-339.

[16] YANG Z, LI X, WANG H, et al. On clutter sparsity analysis in space-time adaptive processing airborne radar[J]. IEEE Geoscience & Remote Remote Sensing Letters, 2013, 10(5): 1214-1218.

[17] SUN K, MENG H, WANG Y, et al. Direct data domain STAP using sparse representation of clutter spectrum[J]. Signal Processing, 2010, 91(9): 2222-2236.

[18] KIM K, SARKAR T K, WANG H, et al. Direction of arrival estimation based on temporal and spatial processing using a direct data domain (D/sup 3/) approach[J]. IEEE Trans.on Antennas & Propagation, 2004, 52(2):533-541.

[19] 阳召成. 基于稀疏性的空时自适应处理理论和方法[D]. 长沙:国防科技大学, 2013.

YANG Z C. Theory and methods of sparsity- based space-time adaptive processing[D]. Changsha: National University of Defense Technology, 2013.

[20] 刘汉伟, 张永顺, 王强,等. 基于稀疏重构的机载雷达训练样本挑选方法[J]. 系统工程与电子技术, 2016,38(7):1532-1536.

LIU H W, ZHANG Y S, WANG Q, et al. Training sample selection for airborne radar algorithm based on sparse reconstruction[J].Systems Engineering and Electronics,2016,38(7): 1532-1536.

[21] Adaptive Systems Lab. The McMaster IPIX radar sea clutter database[EB/OL].[2016-11-07].http:∥soma.ece.mcmaster.ca/ipix.