随机交通网络约束最可靠路径问题

潘义勇，陈 璐，孙 璐

(1.南京林业大学汽车与交通工程学院，南京210037；2.东南大学交通学院，南京210096；3.美国Catholic大学 土木工程系，华盛顿特区DC 20064，美国)

0 引言

最优路径问题是车辆导航系统的核心问题，现有的导航系统没有考虑交通网络的随机特性和路径选择时的约束条件[1].一方面，交通网络中行程时间具有随机性，需要研究考虑可靠性的最优路径问题；另一方面，驾驶员在选择最优路径时都会受到各种约束条件的限制，例如行车距离，机动车的油耗，电动汽车的蓄电能力等，因此需对随机交通网络环境下约束最可靠路径问题进行研究[1].

目前，对随机交通网络环境下无约束最优路径问题研究的很多，主要有最小期望路径问题[1]和最可靠路径问题[2]，其中最小期望路径问题没有考虑由于交通网络随机特性带来的风险性，最可靠路径问题考虑了路径可靠性的路径选择行为.最可靠路径问题由于其考虑可靠性的路径目标函数定义的不同，其最可靠路径模型及其求解算法也是不同的，主要有：最小期望—均方差路径，最优期望效用路径，最大可靠度路径，α—可靠路径等[2]，其中最小期望—均方差路径最能直接反映路径的可靠性[3]，另外，当路径的随机行程时间服从正态分布时，其他几种考虑可靠性的路径目标函数可以表示为期望和均方差的线性组合，本质上也就转化为最小期望—均方差路径问题，因此本文采用期望—均方差为考虑可靠性的路径目标函数.

针对随机交通网络环境下约束最优路径问题研究的非常少，Wang等首次研究了随机交通网络环境下约束最小期望路径问题[4]，但是没有考虑行程时间的可靠性；潘义勇等研究了考虑可靠性的随机交通网络约束最优路径问题[5-6]，其路径目标函数定义为期望和方差的线性组合，在一定意义上反映了路径行程时间的可靠性，并且由于期望和方差的可加性，求解该问题比较容易，但是期望值和方差不在一个量纲上，因此其求解的结果往往会有偏差.

本文在已有研究的基础上，研究随机交通网络环境下约束最小期望—均方差路径，避免了上述问题，但是由于均方差的非线性和不可加性，其求解更复杂，这是本文研究的出发点.首先，定义期望—均方差为路径的目标函数，建立随机交通网络环境下约束最可靠路径问题数学模型；其次，讨论了该问题的对偶问题；第三，采用梯度下降算法求解对偶问题，获得原问题最优值的上界和下界，通过迭代逼近获得原问题的近似解；第四，编写计算机算法程序，并针对实际交通网络Sioux Falls network展开数值试验并对计算结果进行了分析；最后，总结了本文的研究成果及进一步研究的方向.

1 问题描述与建模

交通网络G=(N,A,X)，N(||N=n)是交通节点的集合，A(|A|=m)是边的集合，其中边相当于交通网络中的路段.每个节点i都有若干前节点和后节点与之连接，前节点的集合记为Φ(i)={j,(i,j)∈A} ，后节点的集合记为Φ-1(i)={k,(k,i)∈A}.边(i,j)的2个权值设置为该路段的行程时间tij和资源消耗wij.交通网络中行驶者不仅考虑行程时间，还会受到不同资源的约束，例如，电动汽车耗电量作为路段资源消耗权重，那么该电动汽车的电池总容量就是其资源总消耗的上限值；机动车碳排放量作为路段资源消耗权重，政府规定的碳排放标准可以作为其资源总消耗的上限值.

传统的约束最短路问题针对的是确定网络，其中边(i,j)的2个权值tij和wij是确定值，因此，起讫点(o,d)之间的约束最短路径问题可以描述为0-1整数规划问题，即

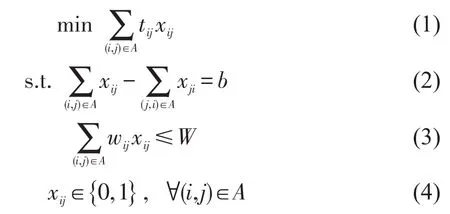
由于行程时间的随机特性，因此边(i,j)的权值tij为随机变量，其期望值cij和均方差σij可以通过历史数据获得.针对这样的随机网络，研究人员定义各种路径目标函数来反映行程时间的可靠性，其中最能直接反映行程时间可靠性的是期望—均方差路径问题，定义路径的目标函数为

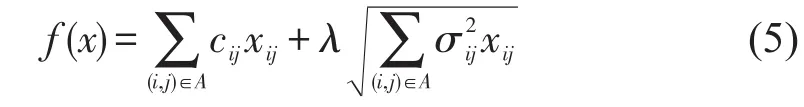
均方差是用来度量随机变量和其期望值之间的偏离程度.把均方差加入到目标函数，可有效控制偏离程度，反映了该路径行程时间的可靠性.本文把上述确定网络环境下的传统约束最短路径问题扩展到随机网络环境下的约束最可靠路径问题，即

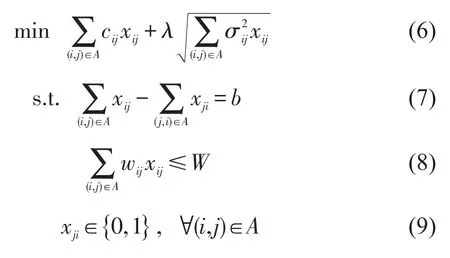
Wang等首次研究了随机交通网络环境下约束最小期望路径问题[4]，但是没有考虑行程时间的可靠性.本文采用期望值和均方差线性组合为路径目标函数，在目标函数里面添加了均方差，考虑了路径行程时间的可靠性，并且期望值和均方差在一个量纲上.但是由于均方差的非线性和不可加性，相对于文献[4]的约束最优路径问题，大大增加了求解该问题的难度，因此讨论其对偶问题，从而获得其近似最优解.

2 对偶问题

求解最可靠路径问题式(6)～式(9)的精确解非常困难，本节首先通过松弛变换获得原问题的松弛问题[7]，其次运用拉格朗日对偶理论[7]对上述约束最可靠路径问题进行讨论，获得原问题的对偶问题，求解其对偶问题获得原问题最优解的最大下界.

由于目标函数式(6)中含有非线性函数，因此我们需要通过变换转化该非线性，其中目标函数式(6)等价于：

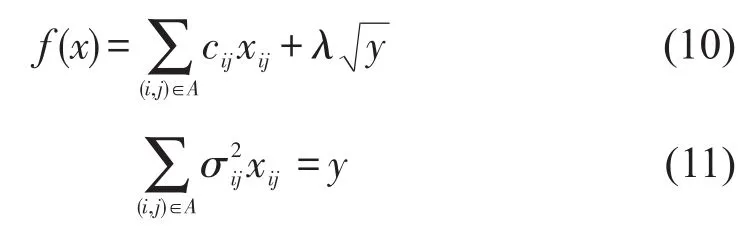
虽然增加了1个变量y，但是式(11)可以转化为原问题的约束条件，并且根据拉格朗日松弛理论，式(11)可以转化为不等式约束条件.

定理1[7]0≤y≤y′，其中y′是最小期望路径的方差.

因此，随机网络环境下的约束最可靠路径问题式(6)～式(9)可以转化为

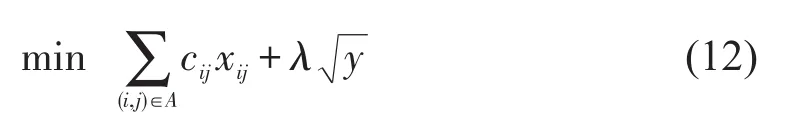
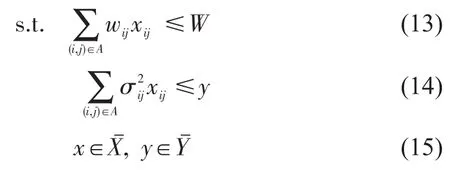
下面我们根据拉格朗日对偶理论推导出式(12)～式(15)的对偶问题，对于任意的拉格朗日罚因子μ=(μ1,μ2)≥0，和，定义拉格朗日函数为

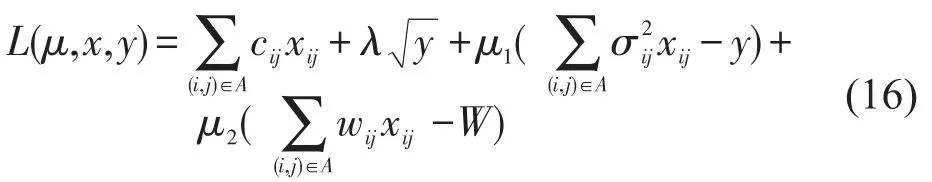
通过整理可得

其中，

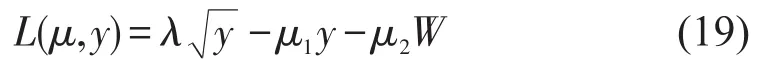
并且，

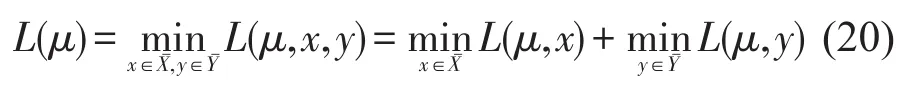
对于给定的拉格朗日罚因子μ=(μ1,μ2)≥0，其中第1个子问题是传统的最短路径问题，可以通过经典的标号算法求解；第2个子问题是非线性约束优化问题，由于其目标函数式(19)是凸函数，因此其最小值只能在区间的两个端点处取到，因此式(20)可以通过其两个分解的子问题简单求解.

根据拉格朗日对偶理论，对于任意的拉格朗日罚因子μ=(μ1,μ2)≥0，式(20)是原问题式(6)～式(9)最优值的下界，即

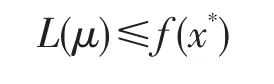
式中：f(x*)为原问题式(6)～式(9)的最优值.

原问题式(6)～式(9)的对偶问题为

根据拉格朗日对偶理论，对偶问题式(21)的最优值是松弛问题式(12)～式(15)的下界最大值.

3 求解算法

本节采用梯度下降算法[7]求解对偶问题式(21).该迭代算法每次选取目标函数的负梯度方向作为搜索方向，并且常依据目标函数的梯度来确定搜索步长.在每次迭代步中，对于给定的μ=(μ1,μ2)≥0，通过求解式(20)获得原问题的下界，求解最短路问题式(18)或者其K-最短路问题可以获得原问题的上界，通过对μ=(μ1,μ2)≥0迭代不断缩小上下界之间的差距，当上下界之间的差小于等于理论差值时，获得式(9)的最优解.具体的算法步骤如下.

Step 1初始化.

设k=1，其中k是迭代步数；初始UB=+∞，LB=-∞，其中UB表示原问题式(9)的上界,LB表示原问题式(9)的下界；初始的拉格朗日罚因子μ=(μ1,μ2)≥0随机给定.

Step 2计算下界.

Step 3计算上界.

Step 4修正拉格朗日罚因子.

首先，确定拉格朗日罚因子(μ1,μ2,μ3)修正的搜索方向，其搜索方向为拉格朗日函数关于μ=(μ1,μ2)≥0的梯度方向，即

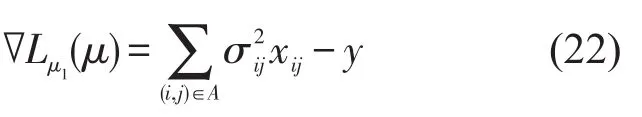
修正拉格朗日罚因子(μ1,μ2)为

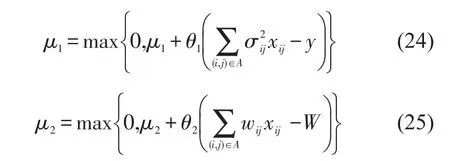
Step 5计算误差.

4 数值试验

本节对上述算法的可行性和正确性进行数值验证，采用国际标准的测试交通网络Sioux Falls(SF)network[5]，如图1所示.由于实际历史交通数据的缺失，需要在Sioux Falls(SF)network拓扑结构的基础上，对其网络边的权值进行数值模拟，从而获得带资源约束的随机交通网络，交通网络中边(i,j)的行程时间tij是随机变量，其期望值cij和方差是确定值，分别从区间[0,20]min取随机数给定.交通网络中边(i,j)的资源消耗wij是确定值，从区间[0,20]min取随机数给定.上述期望值cij，方差和资源消耗wij一经给定就固定不变.这种模拟不影响对本文提出的模型及其算法的数值验证，本文提出的约束最可靠路径模型及其算法不受网络边的权值设置的影响，具有普适性.

基于Matlab计算机语言编写本文提出的算法程序，并且在Windows-10(64)工作站(two 2.00 GHz Xeon CPUs and 4G RAM)条件下运行的.为了对模型中不同参数的灵敏度进行分析，本节对不同情形下的约束路径问题进行了数值实验，并对数值结果进行了分析.

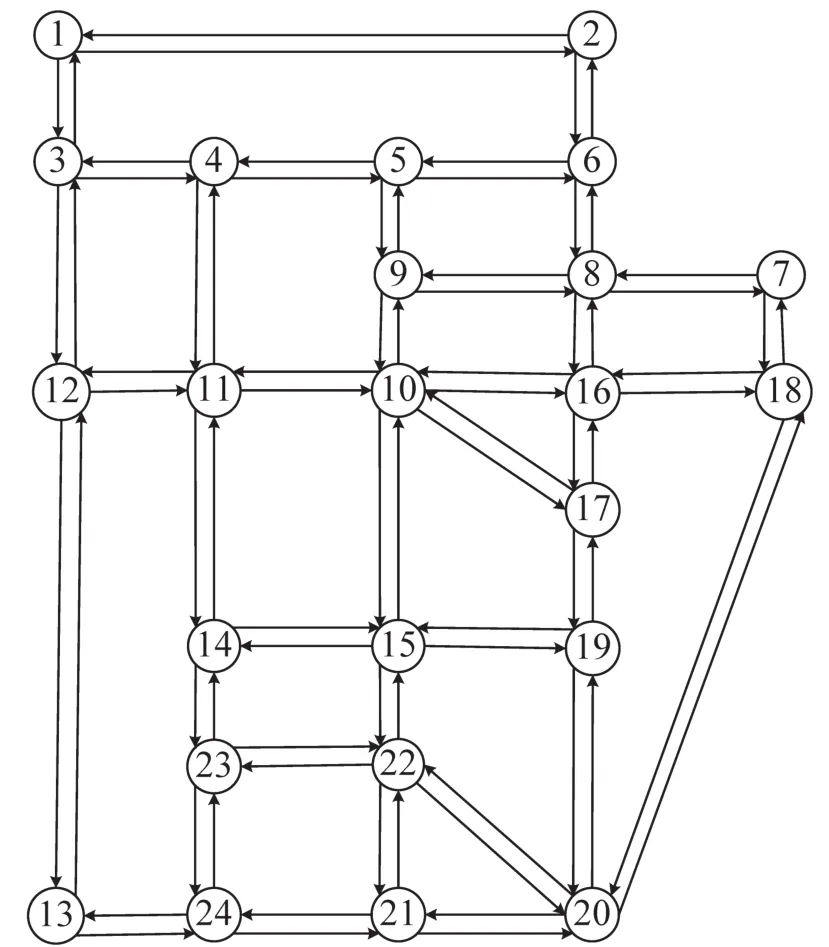
图1 苏福尔斯网络Fig.1 Sioux Falls network

图2分别给出当起迄点设置为4→15时上界UB和下界LB随迭代次数的变化图，其中初始参数的设置为ε̂=0.05，W=60，λ=2，从图2中可以看出，随着迭代次数的增加，上界UB逐渐减小，下界LB逐渐增大，最终逼近于最优值.这和算法的理论设计是一致的，验证了本文构造的算法的可行性和正确性.由于初始给定的上界UB=100和下界LB=-100，因此迭代开始阶段下界保持LB=-100，随着迭代次数的增加，下界LB开始增加，这证明本文推导的原问题的对偶问题是正确的，对偶问题的最优解是原问题最优解的最大的下界.

图2 上界UB和下界LB随迭代次数的变化图Fig.2 The variation of upper bound UB and lower bound LB along with number of iterations

表1给出了在ε̂=0.05，λ=2条件下，不同起迄点和不同的资源上限W的资源消耗，最优值的上下界，相对误差，以及最可靠路径，其中W=+∞表示无资源约束条件下的模型求解.从表1中可知，起迄点1→24在不同的资源上限W=50,60约束条件下，其获得最可靠路径是不同的；起迄点7→19在不同的资源上限W=30,40约束条件下，其获得最可靠路径是不同的；起迄点2→23在不同的资源上限W=40,55约束和无约束W=+∞条件下，其获得最可靠路径是不同的.

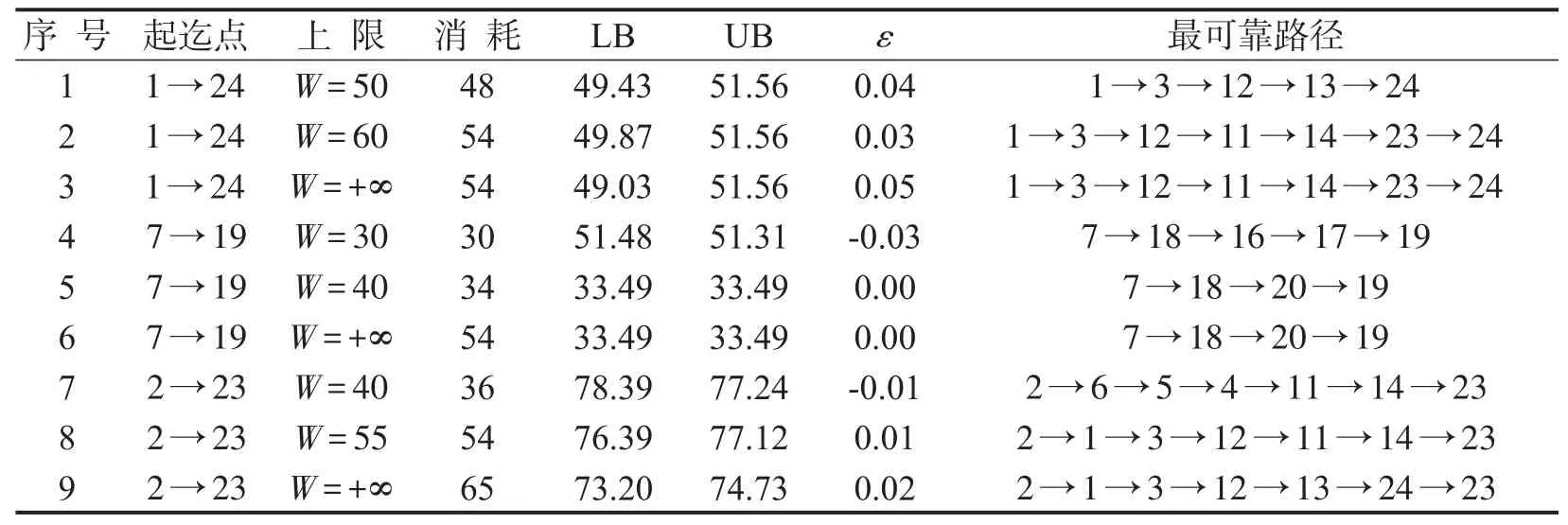
表1 不同资源总量约束条件下最优路径和最优值(1→24)Table 1 The optimal path and the optimal value under different resources constraint(1→24)

由此可以看出：

(1)有资源约束和无资源约束条件下，相同的起迄点之间的最可靠路径是不同的，有约束和无约束条件下随机交通网络环境下最可靠路径问题具有根本性的不同；

(2)资源约束上限W的取值不同，求解获得的最可靠路径和最优值也是不同的，资源约束条件对路径的选择具有重大的影响，这符合实际交通网络最可靠路径选择情形；

(3)本文提出的基于对偶理论的近似算法能够求解随机网络环境下约束最可靠路径问题，获得最可靠路径和最优解，这有利于我们进一步利用现有软件实现最可靠路径的导航应用研究.

5 结论

针对交通网络中约束条件下考虑可靠性车辆路径选择问题，建立了随机交通网络环境下约束最可靠路径问题数学模型，并讨论了其对偶问题，采用梯度下降算法求解对偶问题，获得原问题最优值的上界和下界，通过迭代逼近获得原问题的近似解，针对交通网络展开数值试验，验证了该模型和算法的正确性和可行性.相比较于已有模型，本文提出的模型能同时反映交通网络的随机特性，路径约束条件的影响及路径选择的可靠性，更符合实际交通网络路径选择情形，本文提出的基于对偶理论的近似求解算法是一个有效的算法.数值试验结果表明：在随机交通网络环境下，无约束和有约束条件下求解的最可靠路径是不同的；不同的资源约束条件下求解的最可靠路径也是不同的，资源约束条件对交通网络中最可靠路径的选择有很大的影响.本文只考虑了交通网络的随机特性，没有考虑其动态特性，考虑动态随机网络环境下约束最可靠路径问题需要进一步研究.

参考文献：

[1]GAO S,CHABINI I.Optimal routing policy problems in stochastic time-dependent networks[J].Transportation Research Part B:Methodological,2006,40(2):93-122.

[2]WU X,NIE Y M.Modeling heterogeneous risk-taking behavior in route choice:A stochastic dominance approach[J].Transportation Research Part A,2011(45):896-915.

[3]KHANI A,BOYLES S D.An exact algorithm for the mean-standard deviation shortest path problem[J].Transportation Research Part B:Methodological,2015(81):252-266.

[4]WANG L,YANG L,GAO Z.The constrained shortest path problem with stochastic correlated link travel times[J].European Journal of Operational Research,2016,255(1):43-57.

[5]潘义勇,马健霄.基于可靠性的随机交通网络约束最优路径问题研究[J].东南大学学报(自科版),2017(6):1263-1268.[PAN Y Y,MA J X.The constrained shortest path problem in stochastic traffic network based on the reliability[J].Journal of Southeast University(Natural Science Edition),2017(6):1263-1268.]

[6]潘义勇,马健霄,孙璐.基于可靠度的动态随机交通网络耗时最优路径[J].吉林大学学报(工学版),2016,46(2):412-417.[PAN Y Y,MA J X,SUN L.Optimal path in dynamic network with random link travel times based on reliability[J].Journal of Jilin University(Engineering and Technology Edition),2016,46(2):412-417.]

[7]XING T,ZHOU X.Finding the most reliable path with and without link travel time correlation:A Lagrangian substitution based approach[J].Transportation Research Part B:Methodological,2011,45(10):1660-1679.