岩基上挡土墙抗倾覆稳定分析的讨论
黄岳文
(广州市水务工程建设管理中心,广州 510640)
0 前 言
本刊2016年第5期刊登的“关于挡土墙抗倾覆稳定性的计算”[1](以下简称“原文”)对笔者发表于岩土工程学报2015年第6期的“关于挡土墙抗倾覆稳定分析的讨论”[2](以下简称“讨论”)提出批评,认为“讨论”提出的挡土墙抗倾覆稳定计算新公式欠妥,“建议仍用传统的公式计算,传统公式合理、意义明确、其结果唯一”。“讨论”的中文参考文献基本均被“原文”引用,如果“原文”作者认真阅读了参考文献,应该对传统抗倾覆稳定分析存在的问题有所认知,正是因为认识到传统抗倾覆稳定分析存在不少问题,这才使得很多专家学者研究倾覆破坏机理,提出新的计算公式。针对传统公式存在的问题和“原文”的批评,笔者在此与“原文”作者作一讨论。本文将从分析单一安全系数通式中的结构抗力和作用效应出发,明确抗倾覆稳定分析情况下的结构抗力(稳定力矩)和作用效应(倾覆力矩),据此推导出与“讨论”同样的岩基上挡土墙抗倾覆稳定安全系数计算新公式,并对抗倾覆稳定力矩和倾覆力矩采用“讨论”理解①情况下的传统公式与新公式进行比较。
1 单一安全系数法
传统的工程结构设计方法,都将有关的参数看成是不变的定值,因此统称为“定值设计法”。但实际上工程结构设计是在大量不确定性和存在某些未知因素的情况下进行的,因此设计者为了保证所设计的工程结构安全可靠,一般情况下设计中都会在经验基础上引入一个大于1的安全系数,即将预测到的在使用期间所受到的最大荷载按一定程度的比例增加,或者把材料的强度极限值适当降低作为所用材料的许用应力,以此作为对荷载、材料强度、施工及运行中的不确定性所取的安全余度[3]。因此,传统设计方法一般也称“安全系数法”。
通常单一安全系数要求满足:
k=R/S≥[k]
(1)
式中:R为结构的抗力;S为结构的作用效应;[k]为许用安全系数,通常由经验确定。式(1)中R和S可以表示为各种形式:可以表示为结构材料的强度与结构的工作应力之比,也可以表示为集中力与其反力之比。如对于抗倾覆稳定分析,就常用作稳定力矩与倾覆力矩之比。
可见,安全系数法的基本思想是:结构在承受外荷载后,结构抗力R应不小于作用效应S。若设计者对结构的抗力和荷载作用效应的理解不同,将得出不同的安全系数值,甚至得出不同的结论。
2 传统抗倾覆稳定分析及其存在主要问题
传统倾覆稳定验算方法是:假定墙在土压力作用下绕墙趾外倾,求出各力对墙趾的稳定力矩M1及倾覆力矩M2,定义前者与后者之比为抗倾覆稳定安全系数(倾覆稳定系数),即
k0=M1/M2
(2)
并要求其值不小于许用安全系数[k0]。
“讨论”指出传统倾覆稳定分析存在的主要问题是:① 没有考虑地基承载力的影响;② 假定墙趾为倾覆支点,而实际的支点必然在墙趾的内侧,地基越软,转动支点就离墙趾越远;③ 对抗倾覆力矩M1、倾覆力矩M2存在不同理解导致得出不同的安全系数值;④ 竖向荷载越大,传统抗倾覆稳定分析算出的安全系数越大,容易形成不正确的安全概念。
对于岩石地基上的挡土墙,一般认为假定挡土墙与地基均为刚体,绕墙趾倾覆是合适的。 “讨论”给出当前对M1、M2的3种主要不同理解,并分析3种对M1、M2的不同理解均存在不合理之处。“原文”不考虑墙前被动土压力的影响,取M1=Ga1+Eya2,M1=Exh(参考图1),属于“讨论”理解①,把倾覆力E(主动土压力)的垂直分力Ey作为抵抗倾覆的作用力,因此倾覆稳定安全数相当于挡墙产生倾覆的实际土压力的水平分力另予增加的倍数,然而土压力的垂直分力则不予增加,对土压力而言,力的分解与合成原理没有得到遵守。
笔者曾以浸水挡土墙抗倾覆稳定计算为例,分析对结构的抗力和荷载作用效应理解不同而得到不同的结果[3]。为简化分析,假定挡土墙为宽2 m、高4 m的矩形混凝土结构,自重G=192 kN/m,水深 2 m,墙前后没有水位差,水浮力F=40 kN/m,墙后土压力引起的倾覆力矩为Me=90 kN·m/m,把浮力对墙趾的力矩MF=40 kN·m/m作为倾覆力矩,自重对墙趾的稳定力矩MG=192 kN·m/m,代入式(2)则可得稳定系数k0=192/(90+40)=1.48。而换个思路,把水浮力与结构自重相抵消,即把浸水部分结构采用浮容重来计算,挡墙自重G=152 kN/m,则得到k0=1.69。可见,原文认为的“传统公式合理、意义明确、其结果唯一”的结论并不成立。
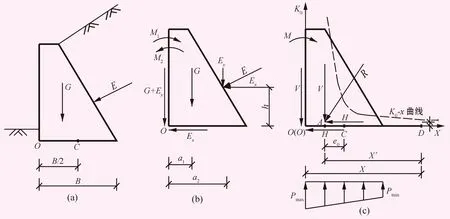
图1 挡土墙荷载图
3 抗倾覆稳定分析
抗倾覆稳定分析的关键在于对抗倾覆稳定力矩、倾覆力矩的正确理解。
“讨论”指出,传统抗倾覆稳定分析之所以存在各种问题,主要是其理论分析的假定前提不合理,其定义本身存在模糊不清之处,容易引起误解。
单一安全系数法的关键是对于结构抗力R和作用效应S的正确理解。在机械设计中,零件或构件的抗力R为所用材料的失效应力,作用效应S为设计应力;当从宏观上分析结构承载安全时,结构抗力R也可取结构理论承载能力,结构的作用效应S可取结构的设计(实际)承受负荷。此时单一安全系数法简单、明了、概念明确。但在某些情况下,结构抗力和作用效应不是那么清晰明了,导致不同设计者有不同的理解,从而得出不同的安全系数值。如对于挡土墙沿基底面抗滑稳定计算中水利设计规范与公路设计规范对抗滑力的理解就不一样[4]。显然,抗倾覆稳定分析的关键还是在于正确确定结构抗力R和作用效应S。
作用效应S在具体工程设计中常取为结构荷载效应组合设计值。在进行挡土墙的稳定分析时,一般假定挡土墙为刚体,挡土墙的稳定决定于结构受到的荷载效应与地基的特性(地基土的强度),结构抗力R只能源自地基的反力。
因此,结构的倾覆稳定系数可按式(3)计算。
K0=MR/MS
(3)
式中:MR为地基抵抗结构倾覆的最大力矩;MS为结构荷载效应组合导致的结构倾覆力矩。
只要挡土墙没有发生破坏,挡土墙的受力是平衡的,对基底截面重心取矩,地基反力提供的抗倾覆力矩都等于挡土墙实际受到的偏心矩。假定地基反力的竖向分力不变,对基底截面重心取矩,此时地基反力能提供的最大抗倾覆力矩为Mmax=N·s,即MR=N·s。而挡土墙实际受到的偏心矩为MS=N·e0。代入式(3),整理可得:
K0=s/e0
(4)
式中:e0为所有外力的合力R在验算截面的作用点对基底重心轴的偏心距,m;s为在截面重心至合力作用点的延长线上,自截面重心至截面前缘的距离,m;对一般挡土墙s= 0.5B,代入式(4)可得:
K0= 0.5B/e0
(5)
如图1 (c)所示,“原文”在A点内侧基底延长线上任选一点D作为转动支点取力矩,由此得到挡土墙抗倾覆稳定计算新公式的普遍形式为:
(6)
式中:K0为X的单调递减函数,函数图象见图1(c)。“原文”认为岩基上抗倾覆稳定计算新公式(5)是式(6)的特例,“适用范围小,只适用A点在C点外侧,即:e0>0;当e0很小时,K0可以很大;当e0→0时,K0→∞;当e0=0时,公式无意义。显然,这是与实际不符的;当A点在C点内侧时,公式不能用。实际工程中A点完全可能在C点内外侧,距离C点可能很近也可能较远,或就在C点。”
对于刚性地基而言,人们的直观判断是“挡土墙要倾倒,应绕前趾转动”。2种不同的抗倾覆稳定安全系数计算方法,式(5)不如式(2)直观,但是正如文献[5]所强调“在科学上不能依靠直观,因为直观往往误人。”在地基承载力满足要求情况下,实际上如果荷载合力穿过基底截面重心(形心),不存在偏心矩就没有倾覆的趋势;“基础产生倾覆稳定性破坏是因为作用于基底上的偏心力矩太大”[6]。这就是推导新公式时对基底截面重心取矩的原因。因此,当e0=0时就没有必要进行抗倾覆稳定计算,“当e0很小时,K0可以很大;当e0→0时,K0→∞”这符合人们“偏心距越小越安全”的经验认知,看不出哪里“与实际不符的”;当A点在C点内侧时,挡土墙存在向内侧(墙踵)倾覆的趋势,式(5)仍可使用,这从另一方面说明所谓通式(6)的不合理。
JTG D63-2007条文说明将合力移到验算截面重心后再对前趾取矩,取稳定力矩与倾覆力矩之比为抗倾覆稳定安全系数。
K0=My/Mo
(7)
式中:My为把全部竖向力移至基底截面重心对截面边缘的抵抗倾覆力矩,My=s∑Pi;Mo为全部外力对基底截面重心的倾覆力矩,Mo=∑Piei+ ∑Tihi。
式(7)有些不好理解,看起来与地基反力没有关系,但如果My换个说法,“My为把地基反力的竖向分量移至截面边缘对基底截面重心的抵抗倾覆力矩”,那么My就是在假定地基反力的竖向分量不变情况下地基抵抗结构倾覆的稳定力矩MR,Mo就是MS。此时式(7)与式(3)等效。
(8)
4 两种抗倾覆稳定分析方法的比较
传统抗倾覆稳定分析对稳定力矩M1、倾覆力矩M2存在不同理解导致得出不同的安全系数值,工程上常采用“讨论”理解①:抗倾覆稳定力矩为全部竖向荷载对墙趾的力矩之和,即M1=∑MV;倾覆力矩为全部水平荷载对墙趾的力矩之和,即M2=∑MH。按图2基于理解①的传统公式(2)可写为:
(9)
下面对传统方法的式(9)与新公式(4)进行比较。自式(8):
记α= ∑Piei/∑Tihi,代入上式得:
K0=(k0+α)/(1+α)
(10)
将式(10)移项整理后可得k0和K0两者关系式:
k0=K0+α(K0-1)
(11)
由式(11)可知:当α>0,即∑Piei与∑Tihi同方向(竖向合力作用于截面重心外侧,多出现于重力式挡土墙),同时又考虑一般情况下K0均大于1,k0>K0,也就是说传统公式算出的安全系数将大于新公式;当α<0,即∑Piei与∑Tihi反方向(竖向合力作用于截面重心内侧,多出现于仰斜式挡土墙)时,k0 图2 倾覆稳定验算示意图 (1) 传统抗倾覆稳定分析由于其理论分析的假定前提不合理,存在各种问题,“原文”认为的“传统公式合理、意义明确、其结果唯一”的结论并不成立。 (2) 荷载对结构的偏心矩是倾覆力矩,地基反力对基底截面重心的力矩是抵抗结构倾覆的稳定力矩。假定地基反力的竖向分力不变,作用点移至基底前缘,可得到地基反力能提供的最大稳定力矩,据此可推导出岩基上倾覆稳定安全系数的新计算公式。 (3) 在传统倾覆稳定计算公式取稳定力矩为全部竖向荷载对墙趾的力矩之和、倾覆力矩为全部水平荷载对墙趾的力矩之和的情况下,竖向合力作用于基底重心外侧时,传统公式算出的安全系数将大于新公式;竖向合力作用于基底重心内侧时,传统公式算出的安全系数将小于新公式;竖向合力作用于基底重心时,传统公式算出的安全系数等于新公式。 参考文献: [1] 姚存楷,吴 钊.关于挡土墙抗倾覆稳定性的计算[J].西北水电,2016 (05):20-23. [2] 黄岳文.关于挡土墙抗倾覆稳定分析的讨论[J].岩土工程学报,2015(06):1158-1163. [3] 黄岳文.从安全系数到风险分析[G]//陈祖煜.水利水电工程风险分析及可靠度设计技术进展.北京:中国水利水电出版社,2010: 352-360. [4] 黄岳文.挡土墙沿基底面抗滑稳定计算的讨论[J].人民黄河,2016,38(02):108-113. [5] 周相略.关于挡土墙抗倾复稳定系数计算的讨论[J].中南公路工程,1983(01):45-53. [6] 张国祥,刘宝琛.墩台基底的倾覆稳定系数新定义[J].铁道学报,2001,23(01):72-75. [7] 中华人民共和国交通部.公路桥涵地基与基础设计规范:JTG D63-2007[S].北京:人民交通出版社,2007:135-136.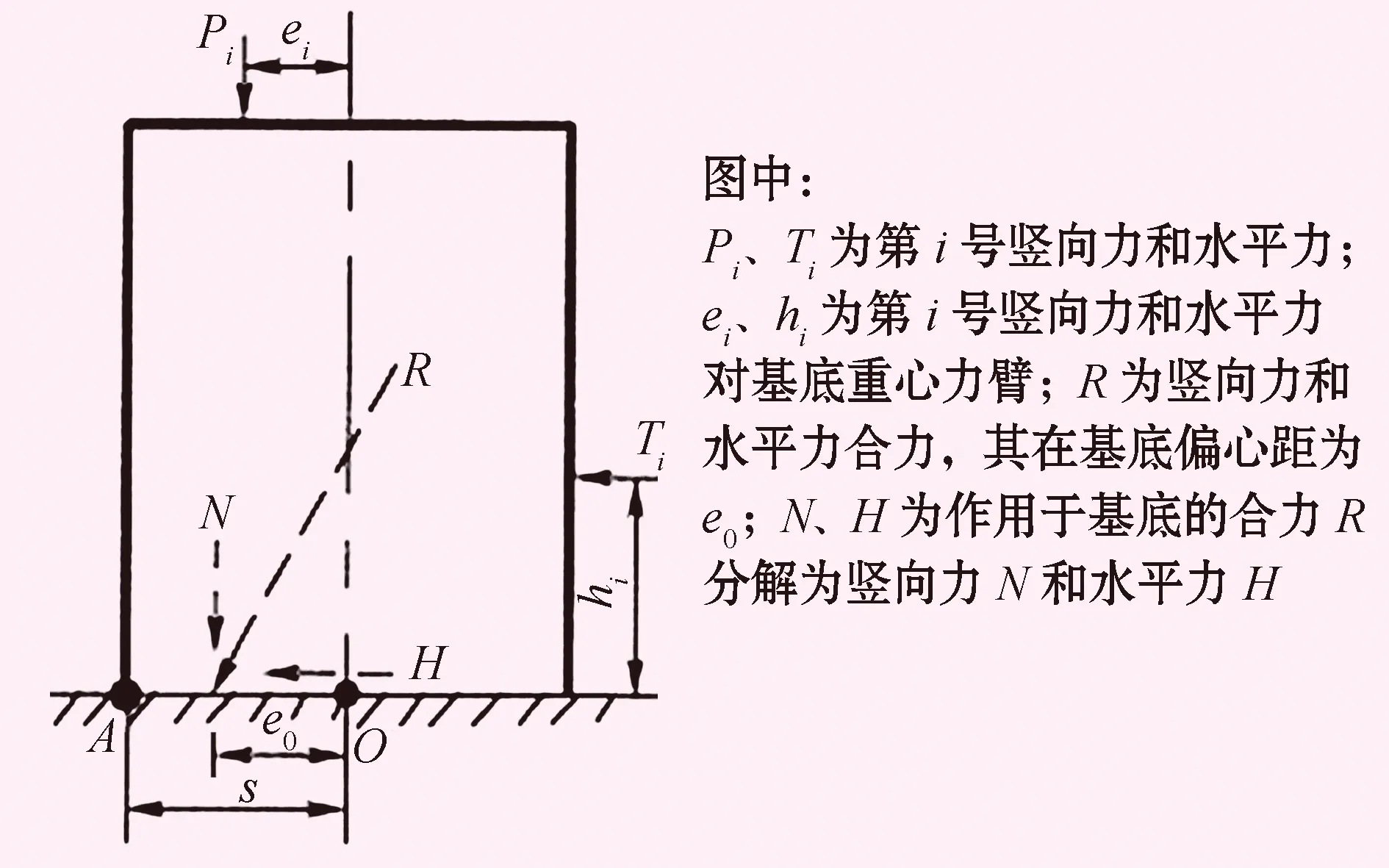
5 结 语

