基于多视几何理论的多旋翼无人机大比例尺测图应用

尚海兴,黄文钰,柯生学,张 钊,马卫昭

(中国电建集团西北勘测设计研究院有限公司,西安 710065)

0 前 言

无人机航测成图已广泛用于大比例尺地形图测绘，但无人机航摄与大飞机航摄相比，获取的影像畸变差大、影像重叠度不规则、像片旋偏角大等技术弊端严重影响了该技术在航空摄影测量领域的应用，尤其是精度要求较苛刻的大比例尺地形图测绘工作[1-2],测图高程精度不达标业已成为无人机航测领域的行业痛点。近年来，基于GPS辅助的空中三角测量技术，在无人机航摄平台上加装差分GPS定位设备，用于测定影像外方位元素的线元素，将其观测值带入加权光束法区域网平差的技术方案一定程度地改善了测高精度(很多情况下仍不达标)，但其使用前提是飞行姿态应尽量平稳并且相机镜头需要严密的相机检校，航摄初始条件要求高。该方案实施门槛较高，硬件成本高，空三精度不稳定。

计算机视觉领域的多视几何(Multiple-view Geometry)[3]与数字摄影测量相似[4]，但理论并不完全一致，2种理论均有其适用前提条件和技术优势。多视几何由于对航摄初始条件要求低，相机无需专业检校，硬件要求低，如何将多视几何理论的优势用于克服摄影测量理论局限性，使之满足测绘工程领域精度要求的研究很有必要。搭载非量测相机的多旋翼无人机灵活易操作，适合小面积地形图大比例尺测绘，多视几何理论成功用于单兵多旋翼无人机大比例尺地形图测绘具有比较现实的应用价值，可为低成本高效地解决小面积地形图测绘提供有力的技术方案。

1 多视几何理论

1.1 多视几何理论原理

多视几何理论是由相机获取的序列影像重构三维场景的三维空间结构和相机曝光瞬间的三维空间位置及方向。其基本思想是：

如图1所示，设空间物点M(X,Y,Z)，相机投影中心O到O′的空间位置矢量t，旋转矩阵为R，2个投影位置相机内参数分别为K1和K2，M在左右片的像点分别为m和m′,设物点M到像点m的投影矩阵为P1，到m′的投影矩阵为P2，即：

m=P1M=K1[I,0]M

(1)

m′=P2M=K2[R,t]M

(2)

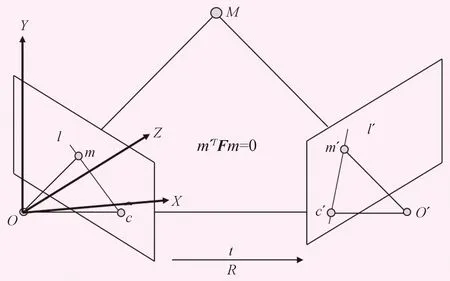
图1 多视几何的核线几何关系图

根据左右片间的核线几何关系[5]，可代数推导出左右像点的关系：

m′TFm=0

(3)

式中：F为基本矩阵，表达了左右片间的核线几何关系，可直接由特征匹配像点坐标计算获取。相机内参数已知时，本质矩阵可由基本矩阵F求得，本质矩阵E由相机的外参数确定，与相机内参数无关，可分解表示为：

(4)

所以，对本质矩阵E进行分解可得到投影矩阵P2，进而获取P1后求得空间点M坐标。本质矩阵分解得到位置矢量t和表示相机方向的旋转矩阵R。计算全程采用代数几何的矩阵运算，未使用泰勒展开式进行线性化处理，物方点坐标M(X,Y,Z)、旋转矩阵R及位置矢量t三个未知数均为任意值。其现实意义是：对影像获取位置和姿态无严格几何约束，定焦相机也无需事前检校，在获取有效像方匹配点后可重构三维场景准确获取物方点坐标。

其计算过程是：① 自动特征提取与匹配；② 利用代数误差的线性估计、几何误差的非线性优化、RANSAC思想的自动估计等算法，计算基本矩阵，在相机内参数矩阵已知前提下，计算本质矩阵；③ 在相机内参数矩阵已知前提下，用基本矩阵分解本质矩阵得到投影矩阵；④ 利用投影矩阵和像点坐标重建对应的物方三维坐标，并分解投影矩阵得到相机空间位置和方向；⑤ 在相机内参数矩阵未知情况下，用投影矩阵进行相机自检校；⑥ 根据自检校的已知相机内参数矩阵和投影矩阵修正三维坐标；⑦ 利用光束法平差原理进行优化估计。

1.2 技术特点

传统摄影测量理论根据像点与物点的几何关系建立约束条件，而多视几何理论，直接由多视角影像像点建立影像间的几何关系，推算相机空间位置与方向及像点对应物点的三维坐标。

传统摄影测量理论的共线方程和共面方程求解未知数是利用最小二乘法原理平差，必须先进行线性化，泰勒级数展开式是原式的近似表达，偏导数所含的仅是微变量，即方程所求的未知数必须具有足够的小值才能得到足够稳定的解，这就需要飞行姿态足够平稳，影像外方位元素具有较为准确的初始值，另外摄影测量理论还需要相机内参数。

多视几何理论的已知数据仅需要多视角影像上的特征像点坐标，允许相机内参数是未知的，相机内参数可通过重叠影像自检校计算获取。其计算过程全自动，计算结果对初始数据非常敏感，所以初始特征点的匹配精度及在影像上的分布对三维模型精度影响较大。

2 实验方案与精度分析

2.1 多视几何航测方案关键技术

2.1.1 航摄方案

多视几何理论成功应用的关键在于像点网的强度与像方连接点的分布和密度，测绘精度达标的成败也在于航摄成果是否满足理想的多视几何理论条件：像方连接点遍布全部重叠区并匹配准确，所以满足理想匹配条件的航摄方案对于测绘精度是否达标至关重要。

(1) 大重叠度、高分辨率航摄

根据测量平差理论，多余观测数越多，平差精度和可靠性就越高[6]。前方交会精度受影像重叠度和交会角大小的共同影响，随着交会角和重叠度的增大，平面精度在逐步提高，使用多片重叠影像同时进行前方交会，平面和高程交会精度都会达到最高[7]。

实际航摄作业中，考虑到交会精度、效率和成本等综合因素影响，航向重叠度保持在80%(航向五片重叠)，旁向重叠度保持在60%左右为宜，以上重叠度指标均需考虑地形起伏，最高点重叠也必须达到。

以两视像对为例，空间前方交会的几何关系如图2所示，空间物方点平面精度mX可表示为：

图2 两视空间交会几何关系图

图3 顾及地形起伏的严密航线设计图

(5)

像点量测精度mx为1/k个像元，则物点平面精度可表示为：

mX=GSD/k

(6)

所以,物点高程精度mh可表示为：

(7)

式中：k为像点量测精度比例尺分母，反映了像点的匹配精度；GSD为地面分辨率；b为摄影基线长度；f为主距。

从式(7)看出影响无人机航测高程精度的因素：① 影像分辨率越小精度越高；② 基线越长精度越高，大重叠的多视航摄条件下，交会角由间隔最大两张影像确定，即多视匹配提高了前方交会精度，同时增强了交会精度的可靠性；③ 与像点坐标量测精度成正比。像点坐标精度由匹配精度决定，所以航摄阶段除了大重叠度航摄外，还需提高航摄分辨率。在多视匹配条件下，每个连接点具备重叠度数较多(8度重叠以上)，物方空间坐标定位稳定性较高，高程精度与平面精度同步，平面精度达标时，高程精度也趋于合格。

基于多视几何理论的倾斜摄影模型精度一般是影像分辨率的约3倍，即多视倾斜测图GSD=正射影像GSD/3。建议的航摄分辨率如表1所示。

表1 多视几何倾斜测图比例尺与航摄分辨率对应表

(2) 顾及地形起伏的严密航线设计

航线设计方案需要基于测区地形起伏进行严密设计，确保全区无漏洞和重叠度，整个摄区具备较均匀的重叠度，有利于在特征提取像点网强度的均匀和可靠性。地形起伏高差过大时需要根据航摄相机主距进行必要的航摄分区划分，顾及地形起伏的严密航线设计如图3所示。

(3) 顾及光照条件的相机参数设置

相机参数设置需充分考虑太阳照度、大气通透性和地物反射强度，光圈设置5.6左右，快门设置最好控制在1/1250 s，ISO需要根据航摄现场光照条件试拍设置，如光线过暗时不建议将ISO曝光补偿提升过大(超过400)，高ISO补偿会导致成像噪点多，后期匹配精度会大幅降低。

(4) 较大面积的弱纹理区域多层航摄

主点和标准点位落水、大面积植被等弱纹理影像处理是摄影测量领域较为空三处理的难题，往往会影响模型相对定向的精度，也是模型接边差过大的要因。同样，基于像方匹配解决物方定位的多视几何理论对像点坐标精度极其敏感，实际作业中为提高影像分辨率往往导致弱纹理区域在单片的面积占比很大，大幅降低了像点特征匹配精度，为提高空三计算的稳健性，降低弱纹理面域在单片上占比，可增加航高，进行多层航摄，在空三计算中联合平差可有效解决该问题。

2.1.2 像控点方案

多视几何仅高精度恢复了物方点的相对关系，其物方坐标与测绘工程中的地面坐标存在尺度、方向和位置上的不一致，所以需要进行绝对定向，足够数量的像控点对提升测图精度很有必要。传统摄影测量领域像控点布设原则，航外规范[8-9]有严格的基线跨度等技术要求，而多视几何理论将地面像控点仅用于绝对定向，像控点可均匀分布，像控点必须置于自由图边外侧。由于多视几何理论具有对像点的唯一依赖，受拍摄条件、相机畸变和像点误差传递的影响，地物点绝对定位精度会在远离像控点处衰减，所以足够密度的像控点格网分布很有必要。

理想的像方匹配结束后，像控点密度可不按照传统的基线跨度布设，可根据表2像控点格网密度进行布设，如图4所示，像控点尽量布设在航带中间便于增加平差时像控点的权重来提高物方测量精度。在自由图边拐弯处必须布设平高点，像控点布设需要考虑加密分区公共像控点的规则分布，这是确保加密分区接边精度的关键。

表2 大疆精灵4Pro的建议像控点分布密度表

2.1.3 空三计算与三维建模

当摄区过大时加密区选择需要根据像控点布设方案进行，加密分区需要重叠1排公共像控点，和1条航带影像。从多视几何原理和特点可知，计算结果对匹配的像点坐标很敏感，所以空三计算前对航摄重叠小、大面积落水、成像不清等影像匹配点精度和分布的原始影像需要进行筛选和预处理。

图4 多视几何理论下的像控点布设方案图

空三加密流程从框架到局部的迭代计算更为稳妥，更易发现像控点粗差。全部像控点添加完毕后，尽量调高像控点权值来提高绝对定向精度，同时减少模型精度对像点的敏感度。

大面积弱纹理区(水域、植被、沙漠)会直接影响像方连接点的密度和精度，很可能造成空三匹配失败无法建模或建模漏洞，测图精度会有不同程度降低，这点也是传统摄影测量理论的技术痛点，多视几何理论可将多层航摄影像数据纳入空三联合平差建模，精度会有一定程度提升，分架次给定不同权值参与平差需根据影像质量和空三人员经验调整。另外，飞行前对航摄相机进行专业的三维检校场检校可获取相机较为准确的内参数，提高像方匹配精度，在弱纹理条件下的连接点分布不均时，可提高相机外参数的估计精度。

2.2 应用与精度分析

2.2.1 飞行平台与传感器

试验采用消费级大疆精灵4Pro无人机影像采集平台。质量轻便易携带，飞行操作简单上手快，起降条件限制少，是很好的小面积地形测绘与建模的影像获取平台。根据顾及地形起伏的严密航线设计方案，对不同测区进行精度估算，采用上述像控点布设方案布设地标式像控点，航摄现场基于DJI SDK二次开发的航摄任务规划地面站，根据像控点分布和加密分区进行严密理论飞行。

2.2.2 实验区选择

选择不同地面分辨率和不同地形特征三类区域对以上方案进行验证，各实验区范围与像控点分布如图5所示。

【A类】：地形平坦，平均高程海拔50.00 m，最大落差30 m，测图面积2 km2，植被水塘较为集中，获取影像402张，像控点22个，检查点30个。预期测绘精度1∶1000地形图。

【B类】：丘陵地形，平均高程海拔3 800.00 m，最大落差100 m，弱纹理草原河道，测图面积12 km2，获取影像6 020张，像控点57个，检查点82个。预期测绘精度1∶2000地形图。

【C类】：山地地形，平均高程海拔200.00 m，最大落差150 m，地表起伏较大，植被茂盛。测图面积4 km2，获取影像2 331张，像控点35个，检查点75个。预期测绘精度1∶2000地形图。

图5 3类实验区像控点分布图

2.2.3 精度分析

多视几何因其公式推导过程未线性化，其结果很难利用传统误差评定方法进行评估，所以目前只可在测绘出的模型精度上进行实测检查。利用RTK方式实测检查点验证三维模型精度，用均方根误差表示位置精度[10]，设检查点实测坐标为Ci(xi,yi,hi)，三维模型量测对应点模型坐标为Mi(xi′,yi′,hi′)，则该点平面误差DXYi和高程误差Dhi用式(8)表达，多个检查点均方根误差SRMSE用式(9)计算。

(8)

(9)

虽无人机行业指导文件[11]对无人机测图精度给出了限差较宽松的B类标准，为提高地形图应用的适用性，本文拟用国家摄影测量内业规范[12]的严苛标准对提出的方案进行精度评价。表4统计出了3类实验区统计的检查点精度指标，比对表3的国标精度限差要求，对实际达到的精度等级给予了评价。图6、7、8对3类实验区检查点精度进行了统计。

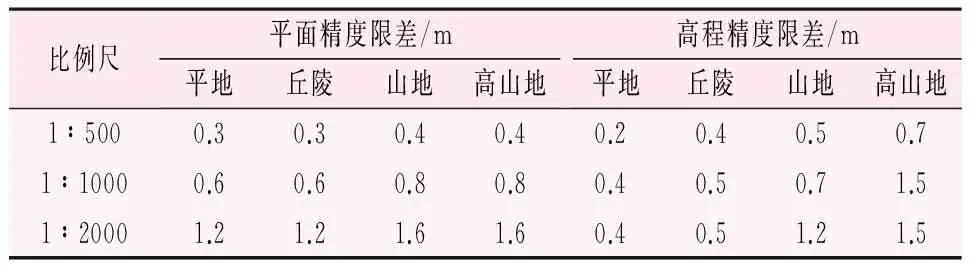
表3 各比例尺地形图精度要求限差表

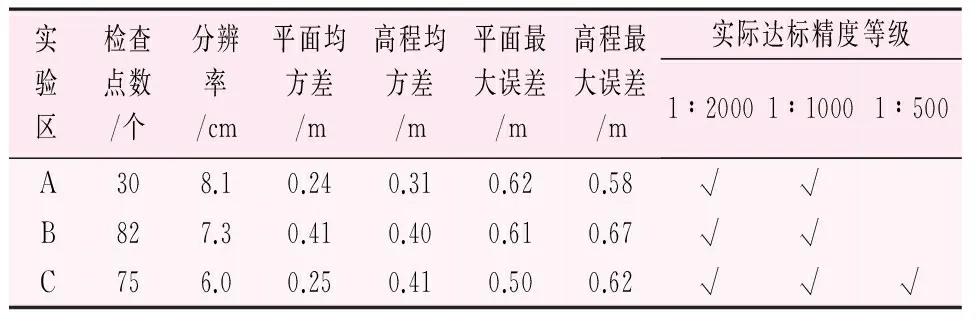
表4 各实验区的检查点精度统计表

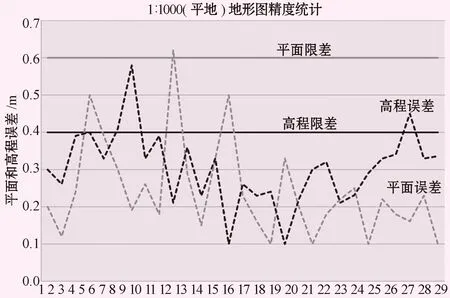
图6 A类实验区检查点精度统计图

实验结果表明：

(1) 根据文中提出的测绘方案，针对平地、丘陵和山地各类地形进行实测检查点精度统计，1∶2000和1∶1000比例尺测绘精度完全满足规范要求，平面和高程精度均同步达标，成功解决了传统摄影测量高程精度较差的行业痛点。

图7 B类实验区检查点精度统计图

图8 C类实验区检查点精度统计图

(2) 根据A、B类实验区精度统计图可看出，平面和高程精度达标时，有少量检查点超限但数量占比极小(<6%)，表明了精度指标的准确性和评价指标的稳定性。

(3) 从表3、4和图8分析，因测区范围较为规则，像控点分布均匀，C类实验区的平面和高程精度达到1∶500地形图精度指标，因植被的干扰，局部检查点高程不符值较弱，所以在测1∶2000和1∶1000地形图时，外业像控点数量可以再减少。

(4) B类丘陵实验区分因地标覆盖大面积草地，属弱纹理区域，航摄时天气变化频繁，多架次匹配等原因，像方网匹配精度较低，因多视几何对像点坐标敏感，所以像控点密度相当时，测图精度稍低于C类山地实验区，这种敏感性表现得很明显。

(5) 航摄分辨率更高、像控点分布更均匀时，平面和高程精度优于1∶500比例尺地形图精度限差。

3 结 语

文中提及的基于多视几何的多旋翼无人机大比例尺测图方案在平地、丘陵、山地均进行了1∶2000、1∶1000、1∶500比例尺地形图精度验证，具备稳定的平面和高程测绘精度。多视几何理论对相机和飞行姿态无苛刻要求，但物方定位精度对像点坐标敏感，所以文中提出了大重叠度高分辨率航摄、顾及地形起伏的严密航线设计、顾及光照条件的相机参数设置、较大面积的弱纹理区域多层航摄的实用航摄方案，同时给出高精度像控点布设方案和空三处理技巧，为消费级多旋翼无人机在大比例地形图高精度测绘提供实用可靠的解决方案。

该方案的技术优势在于：低成本，灵活操作，便于上手,精细的三维模型可以减少外业调绘工作量，相比小面积实测方案减少人员和设备配置，一定程度缩短工期。同时也有其局限性：不宜大面积测图，建模过程计算量较大，建模过程损失电力杆等微小点状地物较多，需要后期补充调绘和补测予以解决。

参考文献:

[1] 任志明,李永树.基于姿态数据的无人机影像自动刺点功能研究[J].测绘通报,2011(04):44-46.

[2] 程婷婷,方源敏.提高我国西南地区空三加密精度的几种方法[J].测绘与空间地理信息,2017(04):216-218.

[3] ANDREW A M.Multiple View Geometry in Computer Vision[J].Kybernetes.2001,30(9/10):1865-1872.

[4] 邓非,张祖勋.基于序列影像的城市三维建模[J].计算机工程,2007,33(08)：208-212.

[5] Hartley R, Zisserman A. Multiple View Geometry inComputer Vision[M].Cambridge: Cambridge University press,2000.

[6] 武汉大学测绘学院测量平差学科组.误差理论与测量平差基础[M].武汉：武汉大学出版社,2003.

[7] 张永军,张勇.大重叠度影像的相对定向与前方交会精度分析[J].武汉大学学报(信息科学版),2005,30(02)：126-130.

[8] 中国国家标准化管理委员会.1:500 1:1000 1:2000地形图航空摄影测量外业规范:GB/T 7931-2008[S].北京：中国标准出版社,2008.

[9] 国家测绘局.低空数字航空摄影测量外业规范:CH/Z 3004-2010[S].北京：测绘出版社,2010.

[10] 张祖勋,张剑清.数字摄影测量学[M].武汉：武汉大学出版社.2012：65-67.

[11] 国家测绘局.低空数字航空摄影测量内业规范:CH/Z 3003-2010[S].北京：测绘出版社,2010.

[12] 中国国家标准化管理委员会.1:500 1:1000 1:2000地形图航空摄影测量内业规范:GB/T7930-2008[S].北京：中国标准出版社,2008.