某电站大坝参数反演分析

王新栋,漆文邦,张江潮

(四川大学,成都 610065)

0 前 言

随着大坝观测技术发展的深入、大坝测量设备精度的提高、大坝监测理论的逐渐成熟，在大坝监测原始观测数据的基础上，利用反演分析来推测坝体混凝土及基岩材料参数的方法业已成熟。反演分析法的原理基于现场测量的位移、应力、应变等数据，通过反演模型推出一些参数(比如弹模、泊松比等)的方法[1]。其最终结果是基于大坝实测数据，建立理论预测模型拟合大坝的各种特征，以此来反馈控制大坝的安全。

位移量是描述物体受力变形形态的一类重要物理量，目前已被用作反演分析确定岩土工程材料特性参数的主要依据[2-3]。

1 工程概况

某水电站是一座以发电为单一目标、具有日调节水库的高水头引水式电站。电站总装机52 MW，设计水头233.00 m，最大水头272.00 m，最小水头233.00 m，加权平均水头258.00 m，最大引用流量24 m3/s，保证出力11.57 MW，年利用小时数5 110 h，年发电量2.45亿kWh。电站水库正常蓄水位1 090.00 m，设计洪水位1 084.60 m，校核洪水位1 088.85 m，电站正常蓄水位以下库容26万m3，调节库容21.2万m3，水库具有日调节能力。本工程属Ⅳ等工程，永久建筑物按4级次要建筑物按5级设计。相应防洪标准，首部枢纽永久性建筑物按50年一遇洪水设计、200年一遇洪水校核。

某水电站首部建有一座有长126.6 m、最大闸高31 m的拦河闸坝日调节水库。首部枢纽从左至右依次布置有左岸锚索边坡、进水闸、泄洪闸(1、2、3号闸)、表孔闸(4号闸)、右岸挡水坝段及右岸护岸工程。进水闸侧向布置在左岸，其轴线与拦河闸坝轴线夹角为50°。闸室前为设有静水栅的静水段和沉砾段，此段与隧洞进水口之间设高程为1 077.50 m的拦沙砍。隧洞进水闸前设有拦污栅，拦污栅底板下布置3孔冲沙孔，孔底高程1 074.00 m，3孔冲沙孔汇集于后面的1.0 m×1.5 m(宽×高)冲砂廊道。3孔泄洪冲砂闸(1、2、3号闸)紧靠进水闸右侧布置，为平底板闸，孔口尺寸7.0 m×8.0 m，每孔设弧形工作闸门各1道，共用1道平板检修门。闸底板高程1 070.50 m，闸顶高程1 091.50 m，闸室长39 m，墩厚分别为2.60 m(边墩，与进水闸分缝)、3.6 m、3.2 m(2号与3号闸墩，中间缝宽2 cm)、3.2 m(3号闸与表孔闸中间缝宽2 cm)。1、2、3号闸基础建基面1 060.50 m。表孔闸(4号闸)紧靠3孔泄洪冲砂闸布置，闸孔宽7.0 m，闸室长39 m。堰顶采用WES曲线，堰顶高程1 083.00 m，溢流面采用400号硅粉混凝土防冲，4号闸基础建基面1 060.50 m。

2 反演分析方法

水利及岩土工程的反演分析可以分为以下几类：位移反分析法、应力反分析法以及二者结合综合反分析法。位移反分析法是目前应用最为普遍的方法，它又分为解析法及数值法。解析法更多的适用于求解较为简单边界条件下的线粘弹性问题，在解决这类问题时解析法优点突出，主要表现在概念明确、计算速度快。相比之下，数值法解决范围更加广泛，且主要用在解决复杂边界及复杂地质条件下的非线性问题。根据数值法的求解过程不同，可以分为正反分析法、逆反分析法等[4-5]。

正反分析法指的是首先指定待反演参数的初始值，通过大型计算软件进行正分析得到典型测点的变位或者应力，之后将计算值与实测值进行拟合比较，当误差较大时通过有效方式调整待反演参数，再重复以上操作直至计算值与实测值之间的误差达到允许的范围内，此时取定的待反演参数值即作为反演计算的最终结果。正反分析方法程序编制简单，计算方法灵活、适用非线性问题的参数反演[6-7]。

逆反分析法与正反分析法的计算程序相反，它是指根据待反演参数与实测值之间的某种关系，直接求解出由该关系式组成的方程组，即可得到反演参数。该方法原理简单直观，且步骤简单，计算用时短，但是需要进行程序编制，且更多情况下适用于线性问题的反演[8]。

考虑到某水电站大坝已进入运行期，经模型有效性初步验证，多元线性回归及逐步回归效果良好，因此本文采用基于多重响应面的位移正反分析法来进行材料参数的反演分析。

基于响应面方法的原理，提出多重响应面方法来拟合坝体参数与大坝在荷载作用下产生的顺河向位移之间的非线性映射关系，相比于其他反分析方法存在的大量的数值计算过程，该方法可以有效减少数值计算次数，节省反分析时间，提高计算效率。

为了保证计算效率和准确度，在本文中，运用不带交叉项的 2 次响应面函数，其表达式为：

(1)

式中：x=(x1,x2,…,xn)为待反分析矢量；a、bi、ci(i=1,2,…,n)为待定系数。式(1)中右端共有2n+1个待定系数，需要有2n+1个方程才能求解。在本文的反分析中s(x)代表位移，x代表待反演参数。

采用响应面法对大坝的各个参数进行反分析，将计算软件内部的计算过程用响应面方程来近似，可大大减少软件的计算次数，提高反分析效率。

3 有限元模型

3.1 变形监测

2013年9月，根据电站监测设施施工设计图及电站现场实际情况，在右岸布置二等单三角控制网，其中BL1、BL3作为日常水平位移监测的工作基点，BL2作为检查点。高程控制点，需由原监测点联测至BL2和BL3，BL2作为垂直位移监测的工作基点，BL3作为检查点。垂直位移监测均采用二等水准进行测量。

垂直位移点和水平位移点均布设在同一位置，参照原设计的点位布设，右岸挡水坝测点编号：LD1，坝顶上游侧测点编号：LD2、LD3，进水口的闸墩测点编号：LD4，下游闸墩测点编号：LD5、LD6。首部枢纽变形监测点布置见图1。

图1 首部枢纽变形监测点布置图

3.2 有限元模型的建立

电站首部枢纽从左至右依次布置有左岸锚索边坡、进水闸(侧向布置在左岸)、泄洪闸(1、2、3号闸)、表孔闸(4号闸)、右岸挡水坝段及右岸护岸工程。本文采用基于多重响应面的位移正反分析法来对电站大坝泄洪闸段某些参数进行反演，分析软件采用大型通用有限元软件ANSYS来进行分析。并将反演得到的参数进行正分析运算，通过应力及变形结果来验证反演参数的合理性。

模型采用D-P准则，坝体与基础网格采用八节点六面体SOLID45单元。

模型采用计算坐标系如下：

X轴,顺河流方向，指向下游为正方向。

Y轴,铅垂方向，铅垂向上为正方向。

Z轴,垂直于水流方向，指向右岸为正方向。

模型范围：

(1) 泄洪闸。泄洪闸坝段由3个闸室组成，其中靠近右岸的2个闸室连为一体，与靠近左岸的闸室用沉降缝分离。泄洪闸三维计算模型仅选取连为一体的2个闸室，闸高31 m。模型边界确定为铅垂方向取至闸室底边界以下62 m；顺河向上游取至闸室上游边界以上50 m，向下游取至闸室下游边界以下50 m；垂直水流方向以闸室左右边界起向左右各延伸50 m。模型共划分51 582个单元，56 210个节点。

(2) 表孔闸。表孔闸闸高31 m。模型边界确定为：铅垂方向取至闸室底边界以下62 m；顺河向上游取至闸室上游边界以上50 m，向下游取至闸室下游边界以下50 m；垂直水流方向以闸室左右边界起向左右各延伸50 m。模型共划分36 156个单元，39 710个节点。

模型边界基础四周和底面采用法向约束，结构顶部及四周采用自由边界。

4 参数反演分析计算

电站泄洪闸坝段及地基共7种材料，每种材料有5个参数，如果全部反演，则工程量十分浩大。从大坝建成到现在已经运行了17 a，随着时间的推移，混凝土的弹性模量也在逐步的变化，因此本文针对影响大坝变形的6个主要参数进行反演分析，依次是基岩t1弹模、基岩t2弹模、基岩t1泊松比、基岩t2泊松比、C10弹模、C20弹模。反演过程中通过2个工况的位移计算值差值与实测差值的拟合度来判定反演参数是否合理。

温度因子是影响混凝土大坝变形的最主要因素，为了尽量减小误差及消除温度场对位移造成的影响，本文选取温差最小、上游水位差值最大且受时效因素影响最小的2015年1月24日(温度6 ℃，上游水位1 084.00 m，下游水位1 065.60 m，定义为工况1)、2015年2月25日(温度6.5 ℃，上游水位1 088.51 m，下游水位1 065.60 m，定义为工况2)2种工况下的实测数据来进行参数的反演。反演过程中通过工况2与工况1的位移计算值差值y2′-y1′与实测差值y2-y1的拟合度来判定反演参数是否合理。根据电站水库运行方式可知：首部枢纽泄洪冲沙闸及表孔溢流坝在枯期(12月-翌年3月)均关闭，可保持水位在1 090.00 m运行。若遇水位超过1 090.00 m时可开启表孔闸门进行调节，以保证水库运行水位在1 081.50～1 090.00 m内运行。而2种工况下的水位上游水位均小于1 090.00 m 。综上可知2种工况下闸门全部关闭。以此来作为荷载施加的依据。

(1) 计算中选用不带交叉项的二次多项式作为响应面函数，共有6 个变量，所以响应面函数有 13个未知量。根据土工试验及地质报告得到的各个物理力学参数的建议值，通过SPSS软件进行正交试验得到13组参数组[9]。

(2) 分别取由第(1)步得到的13 组参数组里面的每一组参数，用ANSYS软件做 13次正分析计算，得到13组泄洪闸坝段的LD2、LD3、LD5、LD6测点顺河向及垂直位移数据。

(3) 对于LD2监测点，将第一组参数值与位移值代入式(1)得到含有13个未知量的一次方程。以此类推，由另外 12 组参数值及位移值可以得到相应的12个方程，总共可以得到由13个线性方程组成的方程组。经求解得到在LD2测点处建立的响应面函数系数。同样的，对LD3、LD5、LD6监测点，采用同样的方法，得到其对应的响应面函数的二项式系数。

将响应面函数的系数值带入式(1)，可得LD2测点的响应面函数。同样方法可得到LD3、LD5、LD6测点的响应面函数。

(4) 建立8个响应面函数方程后，需要找到 1 组参数值，使得由这8个响应面得到的2种工况下的计算位移差值与实测差值之间的差值的平方和最小，即使得目标函数最小。本文采取matlab中的优化工具箱来进行多参数的优化求解，得到的6个待反演参数值如表1所示。

η= [S2H(x)-(0.39)]2+[S2V(x)-(0.2)]2+

[S3H(x)-(1.33)]2+[S3V(x)-(0.1)]2+

[S5H(x)-(0.27)]2+[S5V(x)-(0.4)]2+

[S6H(x)-(0.32)]2+[S6V(x)-(0.2)]2

(2)

表1 反演参数数据表

将6个反演参数值在2种工况下通过ANSYS软件进行正分析，得到LD2、LD3、LD5、LD6测点的顺河向及垂直位移数据计算值的差值与实测值位移数据差值，如表2所示。

可以看出：4个测点中LD2、LD5、LD6的顺河向位移计算差值与实测位移差值都比较接近，只有LD3相差较大。4个测点中LD5、LD6垂直位移计算差值与实测位移差值较接近，LD2、LD3的垂直位移计算差值的符号为负，而实测垂直位移差值符号为正。规定向下沉降为正，向上抬升为负。坝体受到指向下游的推力大于指向上游的推力；同时坝体自身结构分布均匀，底板所受的扬压力从上游往下游逐渐减小。两者共同作用导致坝体所受顺时针方向弯矩。而工况2的上游水位比工况1高4.5 m左右，2种工况的下游水位相等，工况2大坝产生的向顺时针方向的弯矩作用更大，因此工况2位于闸墩上游侧的LD2、LD3测点垂直位移较工况1小，位于闸墩下游侧的LD5、LD6测点垂直位移较工况1大，LD2、LD3垂直位移2种工况下计算值的差值为负，LD5、LD6垂直位移2种工况况下计算值的差值为正是合理的。综上可知，小部分实测数据在观测过程中可能存在一定的误差，大部分实测数据差值与位移计算差值接近，反演参数基本合理。泄洪闸位移云图如图2、3所示。

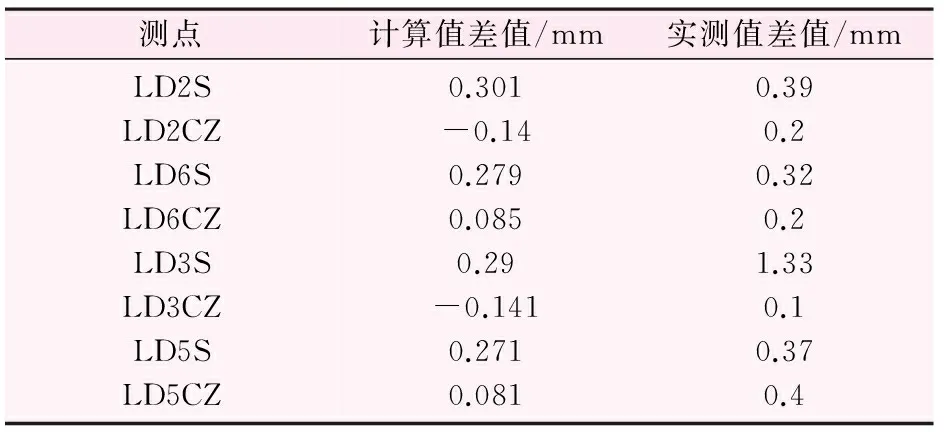
表2 计算值差值与实测值差值数据对比表

图2 泄洪闸顺河向位移云图

5 典型工况下大坝变形及应力分析

5.1 判定标准

(1) 沉降：根据SL265-2001《水闸设计规范》规定，天然土质地基上水闸地基最大沉降量不宜超过15 cm，相邻部位最大沉降不宜超过5 cm。

(2) 应力：依照GB50010-2002《混凝土结构设计规范》规定，混凝土的抗压抗拉强度满足混凝土强度设计值的要求，计算所用到混凝土强度设计值：C20，抗压9.6 MPa、抗拉1.10 MPa；C40，抗压19.1 MPa、抗拉1.71 MPa。

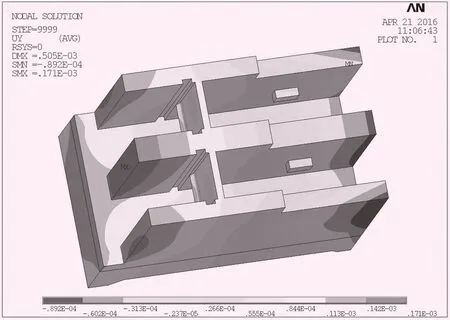
图3 泄洪闸垂直位移云图

5.2 选取的计算工况

(1) 正常蓄水位工况：上游1 090.00 m，下游无水。

(2) 设计洪水位工况：上游水位1 084.60 m，下游水位1 073.80 m。

(3) 校核洪水位工况：上游水位1 088.85 m，下游水位1 072.20 m。

利用反演出的参数，对泄洪冲沙闸及表孔闸在正常蓄水位工况、设计洪水位工况、校核洪水位工况3种工况下进行了安全性论证，结果表明：

(1) 3种工况下泄洪闸的位移值均较小，且对比可知正常蓄水位工况下泄洪闸的位移值最大，最大顺河向位移产生于闸墩顶部，位移值为1.46 mm，最大竖向位移发生于闸墩下游顶部，位移值为-2.75 mm。表孔闸在对应工况下变形规律与泄洪闸类似，在正常蓄水位工况下表孔闸的位移值最大，最大顺河向位移产生于闸墩顶部，位移值为0.75 mm，最大竖向位移发生于闸墩下游顶部，位移值为-2.6 mm。两坝段在3种典型工况下变形均在规范允许范围之内，是安全的。

(2) 3种工况下将大小主应力进行对比发现，泄洪闸在正常蓄水位工况下应力最大，最大压应力为-1.63 MPa，出现在闸墩与闸底板相接处，最大拉应力为1.99 MPa，出现在牛腿与边墩的接触面上。表孔闸在校核工况下应力最大，最大压应力为-1.4 MPa，出现在闸墩与闸底板相接处，最大拉应力为0.233 MPa，出现在溢流面处及闸室下游的末端位置。两坝段在3种典型工况下应力均在规范允许范围之内，是安全的。

综上所述，反演参数基本合理且安全，反演方法正确可行。

6 结 语

本文通过分析研究多种反演分析方法，结合电站监测资料，采用非线性问题的位移正反分析方法。位移正反分析法基于正演分析，方法灵活，程序简单，适用于电站大坝参数的反演。通过对某电站大坝泄洪冲沙闸及表孔闸进行了有限元模拟，采用基于多重响应面的位移正反分析法，对影响大坝位移的基岩t1弹模、基岩t2弹模、基岩t1泊松比、基岩t2泊松比、C10弹模、C20弹模进行了反演分析。结果表明：计算值与实测值中大部分值拟合的较接近，参数反演基本合理且参数反演方法正确可行。同时利用反演分析得到的参数通过对泄洪冲沙闸及表孔闸2个闸坝段在正常蓄水位、设计洪水位、校核洪水位3种工况下进行了变形及应力分析。位移分布符合实测规律，位移值及应力值在规范允许范围内，参考类似工程，反演参数值合理[10]。

参考文献:

[1] 周萍.基于神经网络和遗传算法的岩体参数反分析研究[D].南京：河海大学,2004.

[2] 吴琼.隧道动态设计中围岩计算参数的应力反分析研究[D].成都：西南交通大学,2006.

[3] 周丽君.时空效应下岩质边坡位移反分析研究[D].重庆：重庆大学,2009.

[4] 徐韬.某岩质高边坡稳定性计算与力学参数反分析[D].长沙：中南大学,2013.

[5] 裴建春.混凝土面板堆石坝原型观测资料反馈分析研究[D].天津：天津大学,2007.

[6] 闻世强.茅坪溪沥青混凝土心墙堆石坝反演分析[D].南京：河海大学,2004.

[7] 班宏泰,覃文文,赵昕,柏洪雪,谢鹏,费文平.岩体参数的反演分析方法[J].科技创新导报,2008(08):7-8.

[8] 唐光华.围岩位移反分析及智能化灰色预测与模糊分类的应用[D].武汉：武汉理工大学,2005.

[9] 宁昕扬,刘晓青,牛志伟,齐慧君,潘世洋.基于响应面法的土石坝参数随机反演分析[J].水电能源科学,2017(01):73-76.

[10] 雷晓锋,马双科,郑娅娜.某水电工程地下厂房开挖的岩体参数反分析[J].中国农村水利水电,2017(07):140-143.