基于任务可用度的船舶最佳维修周期模型研究
鲁金明,姚玉南,李泽之
(武汉理工大学能源与动力工程学院,湖北武汉 430063)
维修保养是维持设备正常使用的重要技术手段。船舶设备的维修保养体系经历了3个发展阶段:事后维修、定期维修 (计划预防维修)、视情维修。其中视情维修时以状态检测和预测技术为技术手段,针对设备的运行状态监测数据以及预测结果来确定设备的最佳维修周期,即在故障发生前维修、更换可能发生故障的部件;但是目前存在需要对监测投入较大,对技术要求比较高等问题。现有船舶维修保养体系中还是以事后维修和定期维修为主。定期维修需要解决的关键问题是确定最佳的维修周期,维修周期太长,导致设备的可靠性降低,增加了设备运行的风险;维修周期太短,又增加了设备的维修保养的成本,降低了设备的使用效率。所以确定一个合理的维修周期,对降低设备维修成本、提高设备使用效率具有重要现实意义。
国内很多学者对维修周期展开了研究,取得了相当大的进展。宋之杰等[1]考虑了维修成本的动态变化性,构建了设备预防维修决策模型,该模型以设备单位周期内的总维修成本为目标函数,以设备可用度为约束条件的预防维修周期决策模型。用MATLAB仿真软件对模型进行求解,求解结果证明了模型的有效性。刘栋等[2]对现行三级维修机构保障的复杂设备,以规定可用度为约束条件,以单位工作时间内的平均维修费用最低为目标,建立了设备一个更新周期内,维修周期与维修费用关系模型。王灵芝等[3]人在基于以可靠性为中心的预防性维修计划的基础上分析系统维修费用构成和系统有效度,并以系统总体维修费用最小化、系统有效度最大化为目标,建立多部件成组预防修策略优化模型,提出多部件设备非周期预防维修计划的优化方法。陈雅菊[4]以修理经费和时间作为目标函数,讨论了船舶维修计划多目标问题;利用了该井的非支配排序遗传算法对优化模型进行了求解;为维修计划的制定提供了更多选择。
对于可修系统来说,相比较于可靠性,可用性更能体现系统的可靠性和维修性。可修系统可以停机维修,但出于经济性和任务连续性考虑,一般将严格限定停机时间长短。建模这类系统的可用度的最恰当模型是任务可用度模型。但有关任务可用度的研究尚不多见,所以将系统的任务可用度与维修成本优化模型结合起来,以船舶主动力装置为研究对象,分析其任务可用度。建立以任务可用度、系统可靠度为约束条件,以维修周期为变量的维修费用最低的数学模型,同时利用MATLAB求解模型,并且以典型船舶主动力装置为案例,验证该方法的有效性。
1 维修成本优化模型
1.1 模型假设
设备的维修属于一个目标优化问题,常见的优化目标函数有维修费用最低、停机时间最短、设备的维修周期等。作为可修系统,还需要做出以下假设问题[5]。
1)修复假设。修复假设可分为修复如新、修复如旧以及介于两者之间的不完全维修。修复如新表示修复后设备的故障率如新设备;修复如旧表示修复后部件的故障率与故障发生时的故障率相当。
2)系统任务结果只有2种情况:失败与成功。
3)不考虑部件失效间的差异,每个部件的失效间都相互独立。4)不考虑外部环境、维修方式带来的影响。5)系统修复时间不考虑故障诊断、备品备件的运输时间等间接等待时间。
所以本文构建的维修模型要求系统由相互独立的部件组成,且特征参数服从独立的指数分布,以便利用指数分布的无记忆性求解模型。设备无故障运行到预防性维修周期时间T,则对其进行一次预防性维修。若当该设备工作时间小于预防维修周期时间T时发生故障,则对其立刻进行修复性维修,修复完成后设备继续投入工作直至工作时间累积到预防性维修周期,再对其进行一次预防性维修,如图1任务周期所示。
1.2 任务可用度

图1 任务周期
可用度是设备可靠性与维修性的综合体现。可用度的定义:在规定的时间内,系统正处于能完成规定功能状态的概率,可用度有多种表现形式,包括:瞬间可用度、稳态可用度、平均可用度以及任务可用度。假定系统执行某次任务,任务开始到任务结束之间的时间间隔为一个任务周期。系统的任务结果只有任务成功和任务失败2种,那么任务可用度的定义为任务成功的概率。
国外学者针对任务可用度进一步提出了可修系统的任务可用度的定义。对于可修系统,在单次独立失效所需的修复时间不超过维修时限tf条件下,在计划运行时间T(维修周期)内成功执行任务的概率[6],即在任务期间,发生m次故障,每次故障修复恢复时间都在维修时限tf内的的概率公式如下:

式中:F(T)为系统的累计失效分布函数; [Fm(T) -Fm+1(T)]为系统在T内发生m次失效的概率;[G(tf)]m为m次修复中每次修复时间的时间都小于tf的概率;G(t)为修复时间分布函数。
公式 (1)分为2个部分,1-F(T)表示在时间T内不发生故障的概率;后面部分表示在时间T内发生m次故障,每次故障都在tf时间内修复完成的概率。可以理解任务周期中包含2种情形,一种情形是系统在执行任务未发生故障,此时完成任务的概率可以描述为系统可靠性;另外一种情形是系统发生故障,但修复恢复时间未超过限定时间。
1.3 维修成本优化模型
以任务可用度以及可靠度为约束条件,以维修周期为变量,建立总维修成本最低的优化目标函数,建立设备维修成本优化模型如下:

式中:f(T)为总维修费用;Cw为维修成本;Cl为设备停机损失;Cp为预防维修成本;Cc为故障损失成本;βd为设备单位时间停机成本;A(T,tf)代表维修周期为T,修复时间限制tf下的任务可用度;A0为系统的许用可用度;R为系统的可靠度;R0为许用可靠度。
2 模型求解
所建立的维修费用最低数学模型属于非线性规划问题。非线性规划问题的求解需要将模型转变为的标准形式,多变量约束优化问题的标准形式为:

式中:f(x)为目标函数;αx为线性不等式约束;ax≤b代表线性规划问题的不等式约束条件,b为不等式约束的值;c(x)为非线性不等式约束;ceq(x)为非线性等式约束;Aeqx=beq为线性等式约束;lb和ub为变量x的上下限约束。
所以将所建立的数学模型变成标准型。

然后利用MATLAB中自带的fmincon函数求解多变量有约束非线性函数的最小值;得到目标函数的最小值以及最佳维修周期。MATLAB中Fmincon的调用格式如下:
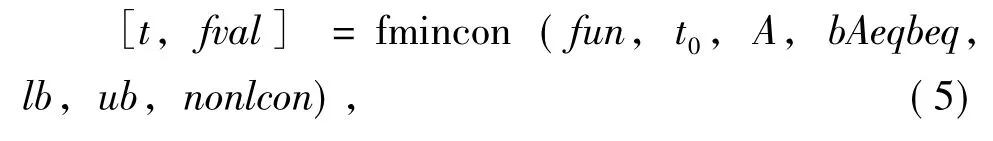
式中:fun代表目标函数;nonlcon表示非线性不等式约束;C(x)≤x和等式Ceq(x) =0的函数句柄。
所以构建相应目标函数以及约束条件函数句柄,利用MATLAB中fmincon即可求解。
3 案例分析
船舶主推进系统是船舶的动力来源,它的安全可靠是保证船舶正常航行的前提。根据船舶主推进系统功能图,得到其系统可靠性框图;如图2是一个典型的船舶动力系统可靠性框图,从图2可以看出船舶动力系统的结构是比较简单的,都是一些部件的串、并联组合。
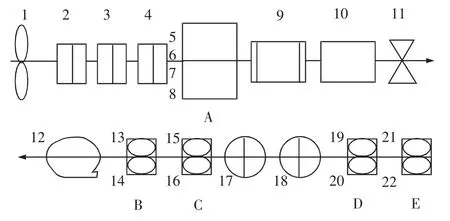
图2 船舶主动力装置可靠性框图
由船舶主动力装置的可靠性框图中编号A-E的部分可以看成并联冗余系统,其他部分为串联,所以系统的可靠度计算如下:
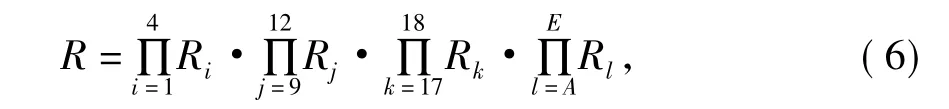
主推进系统在计划运行时间 (0,T]内发生m次故障的概率可由计数过程中泊松过程求得,以下公式表明在时间 (t,t+Δt)发生m次故障的概率:

式中:Λ(t)为累计故障强度函数。
假设系统的失效率服从指数分布,那么将公式(7)代入公式 (3)中得到任务可用度计算公式:

我们假设22个部件的可靠性均服从指数分布,且各部件的失效率查得如表1[7],维修成本如表2所示。
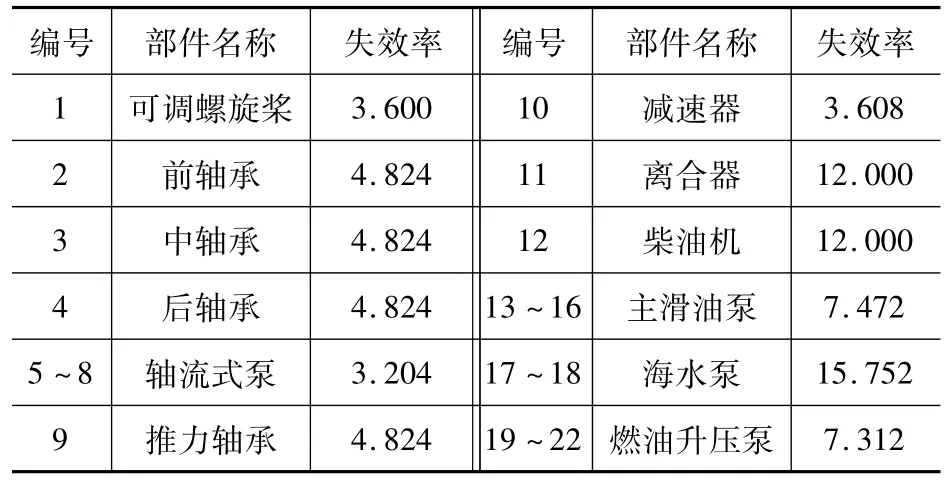
表1 部件故障率 10-6
维修成本如表2所示。

表2 部件维修维护成本 103元
βd设备单位时间停机成本为750元/小时;维修时限为60 h;复杂机械系统的许用可靠度、许用可用度一般取0.9;假设系统的故障率服从指数分布,失效率为1/4 000。利用MATLAB仿真软件对维修成本优化模型进行求解,约束条件为主推进系统的任务可用度以及可靠度,优化变量为系统的计划维修周期T。
将目标函数转变为非线性规划问题的标准形式;利用MATLAB求解优化模型得到T=3 488.4 h,维修费用随维修周期关系如下:
从图3中,维修成本开始随维修周期增加而降低;当维修周期大于3 488.4 h后,维修成本开始上升;符合实际规律。船舶的故障维修保养和传统机械维修维护存在很大的不同,和其他复杂机械可以随时维护维修不同的是,船舶设备的维护维修需要考虑港口信息。船舶在航行过程中,拘于备件、技术条件等原因,很难在航行途中进行维护管理,所以本文得出的最佳维修周期可以作为船舶调度中权衡的因素,在既定的航运任务条件下,以最佳维修周期为参考变量,选择合适的港口来作为船舶维修维护的停靠点。
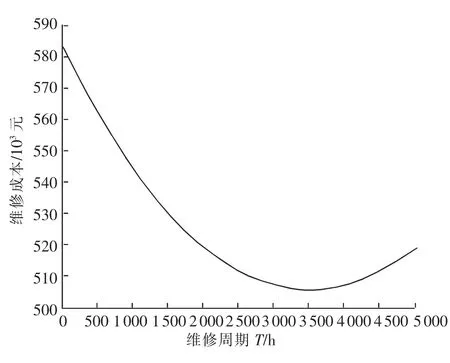
图3 系统维修成本与维修周期的关系
4 结束语
本文针对典型的船舶主动力装置系统,采取故障后维修、定期预防性维修的维修策略,建立了以任务可用度以及可靠度为约束条件,维修周期与维修成本的关系模型,最后以算例验证模型及求解方法的适用性和灵敏性,为船舶主动力装置系统最佳维修周期确定提供参考。
[1]宋之杰,杨志秀,赵玉忠,等.可用度及动态维修成本下的维修决策模型 [J].工业工程,2014(2):17-22.
[2]刘栋,李有为,葛阳.复杂设备最佳维修周期优化决策模型研究 [J].数学的实践与认识,2013,43(20):177-182.
[3]王灵芝,徐宇工,张家栋.基于设备有效度和可靠度的预防修经济优化模型 [J].机械工程学报,2010,46(4):163-168.
[4]陈雅菊.基于多目标遗传算法的船舶修理计划优化研究 [J].中国修船,2011,24(3):46-48.
[5]周瑜.可修系统维修效果评估及维修决策研究[D].成都:电子科技大学,2014.
[6]Attila csenki.Mission Availability For Repairable Semi-Markov Systems:Analytical Results And Computational Implementation[J].Statistics A Journal of Theoretical&Applied Statistics,1995,26(1):75 -87.
[7]杨勇虎.船舶动力装置寿命预测与风险评估的研究及系统开发 [D].武汉:武汉理工大学,2003.

