波浪破碎过程对油滴垂直混合影响的数值模拟及实际验证
,,
(1.国家海洋局第一海洋研究所,山东 青岛 266061;2.海洋环境科学和数值模拟国家海洋局重点实验室,山东 青岛 266061;3.青岛海洋科学与技术国家实验室区域海洋动力学和数值模拟功能实验室,山东 青岛 266061)
海上溢油是造成海洋环境污染损害的主要因素之一。在各种海洋污染中,石油污染无论在发生频率、分布广度还是在危害程度上均居首位。随着世界海洋运输业的发展和海上油田不断投入生产,溢油事故发生频率不断升高,给海洋安全及人民健康带来重大损害[1-2]。
我国近海发生过多次严重的海上溢油事故,如2003年11月在渤海湾发生的“塔斯曼海”轮溢油事故,生态索赔额高达1.2亿元人民币。又如2006年2月发生的“长岛海域油污染事件”,范围波及山东、天津、河北沿岸,是有史以来渤海发生的影响范围最大的油污染事件。在所有这些溢油事故中,对残存油量的估计都是非常重要的一个问题。
在多种作用因素中,波浪破碎导致的混合搅拌效应通过影响油滴垂向混合,从而对溢油海面残存油量估计起到了重要作用。观测表明,高海况下被破碎波卷入水下的溢油量可以达到溢油总量的50%以上[3],所以研究波浪破碎对油滴的垂直混合是研究海上溢油海面残油量随时间、空间变化的重要基础,只有充分了解并掌握这一物理过程,才能够全面地分析和预报海上溢油的变化趋势,可以对溢油分散剂的使用量有一定的指导意义。同时,也可以为溢油事故发生后产生的经济赔偿和生态损失评估提供强有力的理论基础和数据证据。
对波浪破碎与油滴垂直混合之间关系的研究,之前主要采用了观测数据分析和理论研究两种研究手段。Delvigneand等[4]、Tkalich等[5]和孙宝楠等[6]根据实验室数据并结合动力推导给出了波浪破碎与油滴垂向运动之间的一些经验和理论关系表达形式。溢油事故往往发生突然,并没有非常实时的现场观测波浪数据以供分析采用。在这种情况下,数值模式是一种非常有效的应急补充方法,可以由计算得到的各类波浪破碎参数,结合理论分析方法,给出具体时段和地点的海面溢油事故发生后油滴垂直混合情况,进而最终得到海面残油量变化趋势。
之前的分析研究因为现场观测数据的缺乏,导致计算结果的可靠性存在问题。随着卫星观测技术手段的丰富,虽然定量估计残油量仍然难度较大,但是定性评估海面残油量已经成为可能[7-8]。这使得结合理论分析和数值模拟的方法,针对某一具体海上溢油时间开展波浪破碎过程对油滴垂直混合影响研究具有一定可行性。
1 研究方法
针对波浪破碎过程对油滴垂直混合影响开展研究,必须首先建立能够描述包括油滴入水和上浮两个垂向运动过程在内的统一动力方程。同时,为了最终给出海面残油量的估计结果,该动力方程必须结合溢油蒸发模型,共同构成描述海面残油量变化的数学模型。
1.1 油滴入水模型
根据Tkalich等[5]的一阶模型,把油滴垂向运动方程描述为
(1)
式中:Ms为海面浮油的质量;Me为海面以下残油的质量(都是在单位海表面积内);Qo为单位时间单位水体破碎卷入的油滴体积(即卷入率)。
入水油的总质量为:Ma=Ms+Me。在溢油之初,Ma等于溢漏出来的油的初始质量M0。Qo在卷入过程中起着决定性的作用。下面用相似性定理分析Qo的表达形式,其中参与量纲分析的变量有4组。
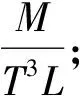
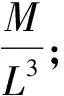
③Z,油滴卷入深度,量纲:L;
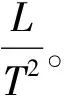
基本量纲为长度量纲L、时间量纲T和质量量纲M,共3个,根据关键变量形成其他变量的量纲一的量方程,求解得到量纲相容方程。
(2)
因为只有一个量纲相容方程,即只得到一个量纲一的量组,因此,有函数形式如下。
(3)
式中:f(x)为待定的函数形式。
选取待定函数为幂函数形式,即令f(x)=cxk,可以得到
(4)
选取最简单的形式,待定系数c=1,k=1。式中Z和E分别为与波浪破碎过程有关的卷入深度和破碎能量损耗率。最终可以得到作用在单位海表面的Qo表达形式为
(5)
取kb=0.5,g=9.8 m/s2,ρw=1 025 kg/m3,Low=1 m。
1.2 油滴上浮模型
油滴上浮的动力过程可用一阶方程描述。
(6)
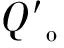
取Lwo=20 m,rc=50 μm,rmax=500 μm,
ρ=900 kg/m3,υ=10-5m2/s,p=2。
1.3 溢油蒸发模型
溢油蒸发方案采用Stiver等[9]提出的分析法模型。
(7)
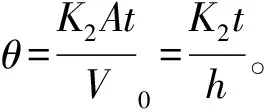
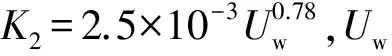
1.4 海面残油量变化模型
综合以上3个子模型,根据Tkalich等[5]的简化方法,海面残油量变化模型控制方程可写为
(8)
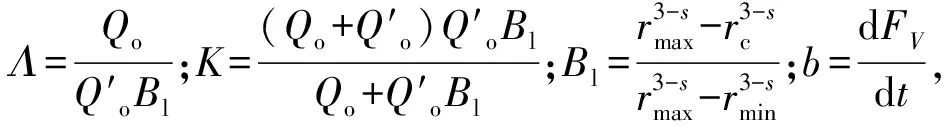
1.5 波浪破碎过程对油滴垂直运动过程的影响
通过已建立的运动学方程发现,波浪破碎主要通过影响Qo对油滴垂直运动产生影响,而该要素主要受与波浪破碎有关的卷入深度(Z)和破碎能量损耗率(E)这两个变量共同控制。针对这两个要素,有多种计算方案可供选择。
针对Z,Delvigne等[4]通过试验室拟合给出的经验表达形式:ZD&S=αHb,其中α=1.5,Hb为破碎波高,取Hb=0.7Hs,Hs为有效波高。Yuan等[11]根据实际海况导出了理论表达形式。
(9)
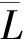
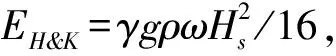
(10)
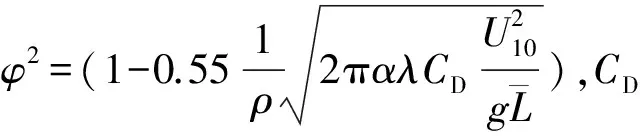
为了分析采用不同计算方案对结果的最终影响,设计3组对比实验,见表1。
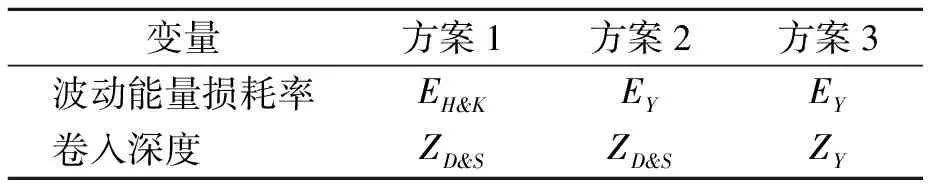
表1 数值试验方案设计
1.6 溢油事件
2006年3月24日渤海湾滦河河口以南曹妃甸附近发生了一起海洋溢油事故。根据当日获取的欧洲空间局环境卫星(Envisat)合成孔径雷达图像判断,该海域形成了大面积的油膜污染,总面积达400 km2。由2006年4月1日获取的Envisat图像判断,渤海湾发生的溢油现象已经减轻,没有发现形态完整、溢出时间较短的油膜。由于波浪破碎携油入水,蒸发等的共同作用,油膜已经分散,质量明显减少,溢油面积减少到100 km2左右,残油量减少了初始质量的75%以上[7]。
1.7 波浪数值模式
为了再现溢油时段的渤海海区波浪平面分布,应用球坐标系下MASNUM海浪数值模式[13]模拟渤海的波浪场。水平分辨率是(1/12)°×(1/12)°,溢油时段为6 d。风场资料采用的是QuickSCAT融合风场数据,计算区域为37°N~41°N,117°E~123°E,模式每小时输出全场波浪要素和破碎参数。
2 结果分析
模拟区域内有效波高Hs和破碎能量损耗率(基于EY计算得到)的空间分布见图1,带色标的底图描绘的是有效波高分布,带数值的等值线描绘的是破碎能量损耗率分布。

图1 模拟得到的不同时段有效波高和破碎能量损耗率平面分布
从整个渤海海区的波高分布上来看,溢油时间段内的日平均有效波高都在1 m以内,2006年3月27日、28日、31日在渤海海峡附近出现了几次大浪过程。渤海湾曹妃甸海域的平均波高在0.3 m左右,在31日最大为0.5 m。从整个区域的破碎能量损耗率上来看,在形态上与有效波高基本相同,波高较高的区域,能量损耗也越大,波高小于0.1 m的时候,破碎能量很小。从溢油区域的波高分布来看,溢油时间段内的日平均浪高在0.3 m左右,在30日、31日两天有相对较大的波浪传入渤海湾,最大波高达到0.5 m。从溢油区域的破碎能量损耗率上来看,25日到29日日平均破碎能量损耗率在0.1 kg/s3以内,30日和31日随着波高的增大最大可达到0.24 kg/s3。
比较溢油点附近两种计算方案所得到的破碎能量损耗率发现(见图2),在有效波高较低的情况下,两种计算方案结果差异不大。但是当有效波高超过1 m时,EY的值陡然上升,对应结果超过EH&K近3倍。
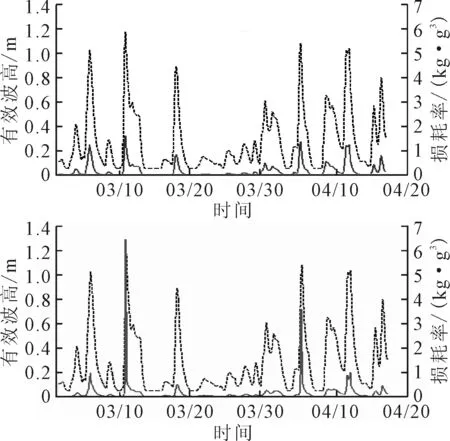
图2 溢油发生点不同计算方案得到的破碎能量损耗率随时间变化情况
计算结果见图3。
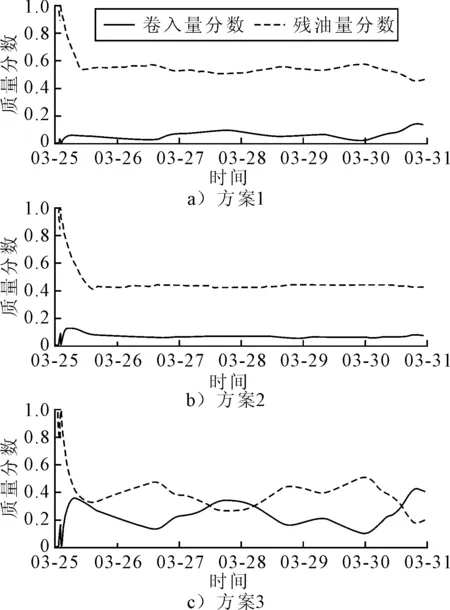
图3 不同实验中海面残油量和卷入量比例随时间变化情况
3个试验在最初的十几个小时内,海表残油量都迅速减少,主要是蒸发过程造成的。方案1和方案2对破浪破碎不敏感,在轻组分蒸发完以后,残油量不再变化。3种试验方案在3月31号的残油量分数分别为45%,41%、20%,见表2。

表2 3组数值试验结果与卫星观测的比较 %
如前所述,欧空局Envisat的雷达数据显示,这一时段的海表残油量最后减少为原来的75%以上[7]。由此可见,方案3的残油量分数最接近这个观测值。
导致这一试验结果的原因可能有以下几点:
首先,方案1和方案2在形态上大致相同,是因为都采用了Delvigne等[4]的卷入深度公式,虽然能量损耗率所选方案不同,但是这一时段渤海湾的海况并不恶劣,两种破碎方案得到的结果比较接近,日平均差大约在0.03 kg/s3左右。所以最终计算得到的结果差别较小。
其次,方案2和方案3相比较,形态差异较大,是因为采用不同的卷入深度方案。实际计算结果中显示,破碎动力水深ZY的值比经验关系式ZD&S的值要小。根据卷入率Qo定义,相同的破碎能量,卷入深度越小,单位时间单位水体卷入的数量越多。所以方案3比方案1和2的卷入分数都要大。最终海表残油量分数要比其他方案小得多,更接近实测值。
3 结论
分析结果显示,采用Yuan等[11]根据实际海况导出的破碎卷入深度和破碎能量损耗率表达式,可以更好地再现油滴在不同波浪破碎背景情况下下沉及上浮的整个过程。通过与Envisat SAR卫星的观测结果相对比,理论与数值模拟相结合的方法,可以很好地重现溢油入海后海面残油量的长期变化趋势。当考虑波浪效应后,估计海面残油量可由40%以上缩小至20%左右,与卫星观测结果中的约25%相比非常接近。
波浪对海面残油量的影响绝非是可有可无的,尤其是在高海况情况下,该效应对海面残油量的估计准确性至关重要。前人根据经验给出的参数化波浪破碎要素计算方案虽然可以大致刻画波浪破碎与油滴垂向运动的关系,但是其准确性和可靠程度低于基于动力学理论推导得到的各要素计算方案。
[1] 秦锐锋,史文强.渤海湾海洋石油开采过程溢油风险预警管理[J].船海工程,2015,44(5):133-137.
[2] 李伟峰,肖中贤,史国友.未确知测度在海上溢油应急能力评估中的应用[J].船海工程,2016(增刊):253-256.
[3] LI, M, GARRETT, C. The relationship between oil droplet size and upper ocean turbulence[J].Marine Pollution Bulletin,1998,36:961-970.
[4] DELVIGNE G A L, SWEENEY C E. Natural dispersion of oil[J]. Oil and Chemical Pollution,1988(4):281-310.
[5] TKALICH P, CHAN E S. Vertical mixing of oil droplets by breaking waves[J]. Marine Pollution Bulletin,2002,44(11):1219-1229.
[6] 孙宝楠,袁业立,韩磊,等.波浪破碎下油滴粒径分布理论模型研究[J].海洋学报,2014,36(9):30-36.
[7] 于五一,李进,邵芸,等.海上油气勘探开发中的溢油遥感监测技术:以渤海湾海域为例[J].石油勘探与开发,2007,34(3):378-383.
[8] 吴晓丹,宋金明,李学刚,等.海上溢油量获取的技术方法[J].海洋技术学报,2011,30(2):50-54.
[9] STIVER W, MACKAY D. Evaporation rate of spills of hydrocarbons and petroleum mixtures[J]. Environ Sci Tech,1984,18(11):834-840.
[10] BUCHANAN I, HURFORD N. Methods for predicting the physical changes in oil spilt at sea[J].Chem. Pollut,1988(4):311-328.
[11] YUAN Y, HAN L, HUA F, et al. The Statistical Theory of Breaking Entrainment Depth and Surface Whitecap Coverage of Real Sea Waves[J]. Journal of Physical Oceanography,2009,39(1):143-161.
[12] KOMEN G J, HASSELMANN S, HASSELMANN K. On the existence of a fully developed wind-sea spectrum[J]. Journal of Physical Oceanography,1984(14):1271-1285.
[13] 杨永增,乔方利,赵伟,等.球坐标系下MASNUM海浪数值模式的建立及其应用[J].海洋学报,2005,27(2):1-7.

