超声波吸收层在天地往返运载器热防护中的应用与研究
吕 鹏,禹彩辉,罗晓光,宫 建,张玉东
(1.中国航天空气动力技术研究院,北京100074;2.空间物理重点实验室,北京100076)
1 引言
天地往返运载器(包括飞船、航天飞机和空天飞机等)作为地面和地球轨道之间往返运送人员和货物的运输工具,是空间站或空间实验室工程系统中重要组成部分。其中,可重复使用的航天飞机或空天飞机的返回方式与一次性使用的飞船截然不同,为滑翔返回式。2011年7月21日,美国“亚特兰蒂斯号”航天飞机顺利降落在肯尼迪航天中心,完成其最后一次太空飞行任务,标志着美国航天飞机历史的终结[1]。航天飞机退役以后,滑翔返回式天地往返运载器仍然是各航天强国的重点发展方向。其中,最为典型的是美国X-37B飞行器,它是一种可重返大气层、可水平着陆、执行在轨试验任务的可重复使用航天器,主要用作空间技术试验与验证平台[2]。
对飞船来说,虽然再入段气动加热特别严重,热流密度极大,但是加热时间短,热载很小,且由于是一次性使用,不严格要求其保持稳定的气动外形和表面平滑度。因此,主要采用烧蚀防热设计。对滑翔返回式天地往返运载器来说,其轨迹相对飞船平稳,热流不如飞船大,但是加热时间长,热载大,并要求保持稳定的气动外形和表面平滑度。因此,需要具有高强度、高韧性、质量轻以及高温环境耐久性好的防热设计。在长时间大气层内滑翔的过程中,边界层的转捩大幅增加边界层热传导系数和摩擦阻力系数[3-4]。如果能延迟边界层的转捩,高超声速飞行器的热载和气动阻力便可以显著降低。这样,从热防护角度来看,可以降低飞行器热防护系统的重量、成本和复杂度;从飞行性能来看,也可以提高飞行速度、增大航程以及扩大飞行器的飞行走廊。
对于二维或者准二维的高超声速边界层,主导边界层不稳定性的是第二模态波,属于边界层中的超声波[5-7]。近年来,通过超声波吸收层(Ultrasonically Absorptive Coating,UAC)吸收超声波进而延迟边界层转捩的方法快速发展。UAC是一种由规则或随机分布的微腔构成的薄层,进入微腔内的声学扰动引起内部空气的剧烈运动,使其与腔体壁面摩擦,在粘性耗散作用下,声学扰动的部分机械能转化成热能。另外,流动中有声学扰动经过时,会产生压缩和膨胀的变化,压缩区温度升高,膨胀区温度降低,相邻压缩区和膨胀区之间的温度梯度会导致热量从温度高的部分向温度低的部分发生热传导。这个过程是不可逆的,声学扰动的部分机械能也会转化成热能。因此,在粘性耗散和热传导的共同作用下,第二模态波的机械能转化成热能,第二模态波不稳定性受到抑制,进而延迟边界层转捩[8]。
Fedorov等人在俄罗斯科学院T-326高超声速下吹式风洞中,来流马赫数Ma=6的情况下,通过热线风速仪测量了尖锥(半锥面是光滑表面,半锥面是 UAC)边界层内的质量流量脉动[9-10]。 实验发现,UAC 稳定了第二模态波,并且对第一模态波几乎没有影响;实验结果中的第二模态波相速度和幅值与理论分析符合良好,初步证明了UAC延迟高超声速边界层转捩的概念。随后,Fedorov等人在美国CUBRC LENS I激波风洞中研究了更高来流马赫数下(Ma=7和Ma=10)UAC对边界层转捩的影响[11],结合可压缩的Blasius基本流和线性稳定性理论(Linear Stability Theory,LST)建立了对应的数值计算模型。研究结果表明,使用UAC可以显著增加边界层中的层流区,UAC稳定第二模态波的能力随着开孔率的增大而增大。除此之外,Fedorov等人还研究了无来流情况下UAC的超声波反射系数[12],以低压实验环境对应高海拔下的真实高超声速飞行情况。在不同压力条件下,理论预测的UAC超声波反射系数均与实验结果符合良好。另外,Fedorov将UAC边界层中第二模态波增长率的理论分析结果与直接数值模拟(Direct Numerical Simulation,DNS)结果进行了对比,发现二者一致性良好,并且都成功预测到 UAC削弱了第二模态波[13]。Fedorov还介绍了由第二模态波主导边界层转捩的美国 HIFiRe-1飞行研究实验[14],进一步讨论了高海拔情况下高超声速飞行过程中的边界层转捩预测问题,并给出了基于UAC的转捩控制方法。
Brès和Colonius等人使用DNS分析了不同声波频率和声波入射角下的UAC超声波反射系数[15-17],DNS结果与理论预测符合良好。由于UAC顶部和底部的反射声波相互叠加,反射系数在某些特定频率处具有最小值或者最大值。相邻微腔之间产生的小尺度散射波表现出声学共振模态。此外,研究结果表明,开孔率和深度是UAC设计过程中最重要的参数[18]。 Brès等人分别利用LST和DNS,对不同宽高比和不同开孔率的UAC材料进行了对比[19]。其中来流条件为马赫数Ma=6,雷诺数(基于边界层厚度)Re=24 000。LST和DNS所预测的第二模态波增长率符合良好。另外,保守的UAC设计方法是使微腔足够深,产生的粘性效应完全吸收进入的声波。此外,Brès等人系统地讨论了UAC的第二模态波削弱机制,以及抵消/增强机制[20]。削弱机制来自UAC微腔内的粘性耗散效应和热传导,其主要表现是超声波反射系数随着频率的增大而单调减小;抵消/增强机制由UAC顶部反射声波和底部反射声波的相位差造成;优化的UAC(最大程度上削弱第二模态波)应该具有高开孔率和相对较浅的深度。
UAC主要可分为随机结构和规则结构,随机结构主要包括金属毡和C/C复合材料,规则结构主要包括槽道、方孔、圆孔等构型[21]。国际上针对UAC开孔率和深度开展了大量的数值计算和实验研究,探讨了开孔率和深度对于UAC吸波特性的影响。截至目前,尚缺乏微腔数量(单位波长范围内)对于吸波特性的系统研究。本文将建立高超声速边界层LST模型,考虑UAC微腔数量对于吸波特性的影响,完善UAC吸波特性的研究。同时对比分析槽道构型和圆孔构型UAC表面边界层中第二模态波的增长率,为未来的天地往返运载器的热防护系统在构型选择上提供技术支持。
2 高超声速边界层LST模型
对于粘性可压缩的理想气体,N-S方程具有式(1) ~(4)所示形式[22]:
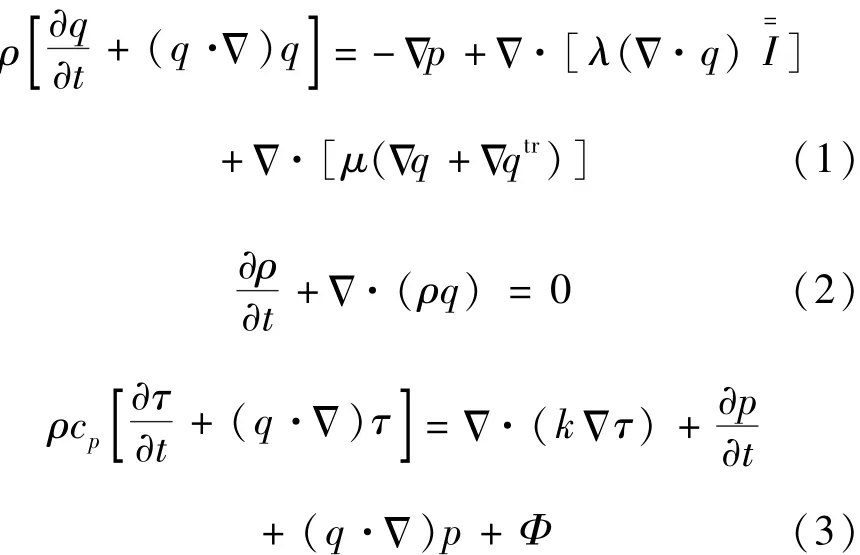

其中,q为速度矢量,ρ为密度,p为压力,τ为温度,R为气体常数,cp为比定压热容,k为热传导率,μ为第一粘性系数,λ为第二粘性系数。粘性耗散项 Φ 由式(5)决定[22]:

LST采用小扰动分析方法,略去相对于基本流可以忽略不计的扰动高阶项,得到扰动的控制方程。对于平板边界层的流动,可以引入平行流假设,其边界层自相似解由式(6)~(7)所示两点边值问题的耦合常微分方程组决定[23]:

其中,普朗特常数 Pr= μcp/k,查普曼-鲁比辛因子c=ρu/ρeue,下标e代表边界层外缘处参数,f′为无量纲速度,g为无量纲静焓。给定壁面边界条件以后,基于四阶龙格-库塔法,由壁面起始进行穿过边界层直到边缘的积分,最终采用打靶方式确定 f″(0) 和 g′(0) 的值。 在线性稳定性研究中,常将扰动模态 ()写成式(8) ~(10) 所 示 形 状 函 数()与 波 状 函 数的乘积形式[23]:

其中,α和β为波数,ω为频率。在时间模式的稳定性问题中,α和β为实数,ω为复数,代表一种在空间上是周期性的,而幅值随时间变化的扰动。ω虚部ωi的正负号决定扰动是增长(ωi>0)或者衰减的(ωi<0),即流动是不稳定或者稳定的。 将式(8) ~(10)带入式(1) ~(4)中,可以得到式(11)形式的稳定性方程:

其中,形状函数φ=^u,^v,^p,T^,^w{},D =d/dy,D2= d2/dy2,A、B 和 C 为系数矩阵。沿壁面穿过边界层直到边缘进行离散化,配置点坐标ξ为式(12):

将计算域中的配置点转化到物理域中的过程中,存在比例因子 S 如式(13)[22]:
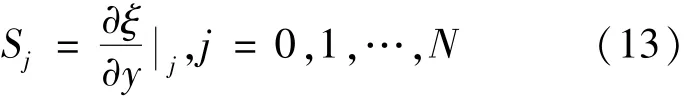
因此可建立物理域中的一阶求导矩阵F为式(14):

其中,E为计算域中的切比雪夫一阶求导矩阵。进而建立物理域中的二阶求导矩阵G为式(15):

式(11)在配置点上具有如式(16)所示形式[22]:

把含有频率ω的部分移到另一侧,式(16)转化成式(17)所示的线性理论方程矩阵形式:

最终,使用 QZ算法(Generalized Schur Decomposition)求解式(17)的广义特征值问题,获得第二模态波的增长率和扰动分布情况。
3 超声波吸收层导纳
求解稳定性方程,需要设定边界条件。通常情况下,稳定性方程的边界条件为:^u(0)=0,^v(0)=χ^p(0),^w(0)=0,(0)=0;^u(∞)=0,^v(∞)=0,^w(∞)=0,(∞)=0。其中χ为介质的导纳。对于普通平板来说,其导纳χ=0。对于槽道和圆孔构型的 UAC来说,其导纳如式(18)[20]:
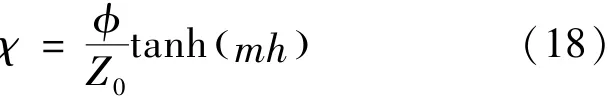
式中,ϕ为开孔率,h为微腔深度。Z0为特征阻抗,m为传播常数,分别由式(19)、(20)定义:


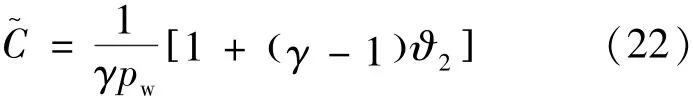
其中,下标w代表壁面处参数;Λ~=对于槽道构型的UAC来说,ϑ1=tanΛ/Λ,ϑ2=tan,无量纲宏观参数 Λ =b是槽道的半宽;对于圆孔构型的UAC来说,ϑ1=QΛ(),ϑ2=Q()(Qx()= 2J1x()/xJ0x(),J0为第一类0阶贝塞尔函数,J1为第一类1阶贝塞尔函数),无量纲宏观参数Λ =r是圆孔的半径。可以看出,超声波吸收层的导纳受开孔率、微腔深度、特征长度(半宽或者半径)影响。
4 结果与讨论
4.1 基本流
为了验证高超声速边界层LST模型,与参考文献进行对比[13,24],计算工况选为位移雷诺数Re=20000,马赫数Ma=6。首先,基于四阶龙格-库塔法,采用打靶方式,计算了对应条件下的绝热壁平板边界层基本流。其中,普朗特数 Pr=0.72,比热比γ=1.4。粘性系数和热传导率由萨瑟兰公式确定。绝热壁平板边界层的基本流结果如图1所示,水平速度和马赫数分布与参考值符合良好[25],成功捕捉到了高超声速边界层基本流的情况。
4.2 模型验证
给定无量纲扰动波长λ=3,扰动波长波数α=2π/λ,配置点数 N=200。 结合4.1节中的基本流结果,使用建立的LST模型,计算普通平板和槽道构型UAC表面边界层中第二模态波的增长率。
对于普通平板来说,特征值的参考值为ωref= 1.9548699 + i0.0339084[13,24],本模型的计算结果为ω = 1.9516780+i0.0332035。第二模态波增长率的相对误差 εi= ωi- ωi,ref/ωi,ref=2.08%,计算结果与参考值符合良好。
另外,计算了四种槽道构型UAC对应的第二模态波增长率。开孔率均为ϕ=0.25,单位波长内的槽道数分别为n=8和n=16。槽道深度分别为h=0.3和h=1.0。表1给出了本模型计算结果与参考值的对比,并给出了相对误差,二者符合良好,验证了本模型在计算第二模态波增长率以及研究超声波吸收层方面的可靠性。

图1 基本流Fig.1 Base flow

表1 第二模态波增长率对比Table 1 Comparison of second mode growth rates
普通平板边界层中第二模态波扰动分布情况如图2所示。可以看出,最大的压力扰动集中在壁面附近,最大的法向速度扰动出现在y=0.3,与参考文献中分布情况一致。图3为槽道构型UAC(n=8,h=0.3)边界层中第二模态波扰动分布。经过对比可以看出,在UAC的吸波作用下,边界层中第二模态波扰动分布发生了明显变化,扰动不再集中,在空间上扩散。
4.3 吸波特性

图2 普通平板边界层中第二模态波扰动分布Fig.2 Second mode disturbance distribution in the flat plate boundary layer

图3 槽道构型UAC边界层中第二模态波扰动分布Fig.3 Second mode disturbance distribution in the flat plate boundary layer
使用建立的LST模型,在开孔率均为ϕ=0.25的情况下,对比分析了槽道构型UAC和圆孔构型UAC的吸波特性随微腔深度h和数量n的变化,如图4所示。在几何参数相同的情况下,圆孔构型UAC对应的第二模态波增长率整体上低于槽道构型UAC。当微腔深度h=0.3,微腔数量n=6,两种构型UAC对应的第二模态波增长率具有最小值。对于槽道构型UAC来说,最小的第二模态波增长率ωi=0.0089,比平板对应的第二模态波增长率低73.20%。对于圆孔构型UAC来说,最小的第二模态波增长率 ωi=0.0053,比平板对应的第二模态波增长率低84.04%。
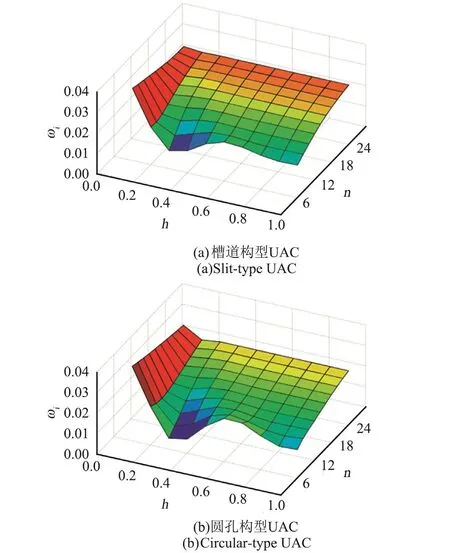
图4 第二模态波增长率Fig.4 Second mode growth rate
第二模态波增长率的最小值出现在微腔数量最少的UAC上。这是由于第二模态波在UAC顶部散射产生了新的高频扰动波,这些扰动波幅值随着微腔数量的减少,特征长度的增加而增大。第二模态波与这些大幅值的扰动波叠加在一起,在一定程度上被抵消。随着微腔数量的增加,这些扰动波幅值降低,抵消效应减弱。图5为圆孔构型UAC(n=6,h=0.3)边界层中第二模态波扰动分布。经过对比可以看出,在UAC的吸波作用下,边界层中第二模态波扰动分布发生了更明显变化,扰动进一步在空间上扩散。
5 结论

图5 圆孔构型UAC边界层中第二模态波扰动分布Fig.5 Second mode disturbance distribution in the circular-type UAC boundary layer
本文建立了基于谱方法的可压缩线性理论稳定性模型。本模型预测的第二模态波增长率与参考数据符合良好,验证了其在计算第二模态波增长率以及研究UAC方面的可靠性。结论如下:
1)几何参数相同的情况下,圆孔构型UAC对应的第二模态波增长率整体上低于槽道构型UAC。
2)当微腔深度h=0.3,微腔数量n=6,两种构型UAC对应的第二模态波增长率具有最小值。
3)第二模态波增长率的最小值出现在微腔数量最少的UAC上,这是由第二模态波在超声波吸收层顶部散射产生了新的高频扰动波所造成。
4)在UAC的吸波作用下,边界层中第二模态波扰动分布发生了明显变化,扰动在空间上扩散。
5)在开孔率一定的情况下,为了提高UAC吸波能力,应当选择较浅的深度(h=0.3)。关于UAC的吸波特性和延迟转捩的效果,有待于通过进一步的实验研究,进行完善。
参考文献(References)
[1] 马野,许健,邵秋虎.后航天飞机时代天地往返运载器发展趋势研究[J].中国航天, 2015(3):17-22.Ma Ye, Xu Jian, Shao Qiuhu.Development trend of space transport vehicle after space shuttle[J].Aerospace China,2015(3):17-22. (in Chinese)
[2] 许红英,侯丹,陈杰,等.美空军发射X-37B飞行器简析[J].中国航天, 2010(6):21-25.Xu Hongying, Hou Dan, Chen Jie, et al.An introduction of X-37B launched by U.S.air force [J].Aerospace China,2010(6):21-25. (in Chinese)
[3] 周恒,苏彩虹,张永明.超声速/高超声速边界层的转捩机理及预测[M].北京:科学出版社,2015:2-5.Zhou Heng, Su Caihong, Zhang Yongming.Mechanism and Prediction of Supersonic/Hypersonic Boundary Layer Transition[M].Beijing: Science Press, 2015:2-5.(in Chinese)
[4] 唐登斌.边界层转捩[M].北京:科学出版社,2015:97-101..Tang Dengbing.Boundary Layer Transition[M].Beijing:Science Press, 2015: 97-101.(in Chinese)
[5] Malmuth N,Fedorov A,Shalaev V,et al.Problems in high speed flow prediction relevant to control[C] //2nd AIAA,Theoretical Fluid Mechanics Meeting,Fluid Dynamics and Co-located Conferences,2013.
[6] Kimmel R L.Aspects of hypersonic boundary-layer transition control[ C] //41st Aerospace Sciences Meeting and Exhibit,Aerospace Sciences Meetings, Reno, Nevada, AIAA 2003-772,2003.
[7] Parziale N J,Shepherd J E, Hornung H G, et al.Observations of hypervelocity boundary-layer instability[J].Journal of Fluid Mechanics,2015,781:87-112.
[8] Fedorov A, Shiplyuk A, Maslov A, et al.Stabilization of high speed boundary layer using a porous coating[C]//41st Aerospace Sciences Meeting and Exhibit,Aerospace Sciences Meetings, Reno, Nevada,AIAA 2003-1270,2000.
[9] Fedorov A,Kozlov V,Malmuth N,et al.Stability of hypersonic boundary layer on porous wall with regular microstructure[J].AIAA Journal, 2006, 44(8):1866-1871.
[10] Fedorov A, Shiplyuk A, Maslov A, et al.Stabilization of a hypersonic boundary layer using an ultrasonically absorptive coating[J].Journal of Fluid Mechanics, 2003, 479:99-124.
[11] Fedorov A, Malmuth N.Parametric studies of hypersonic laminar flow control using a porous coating of regular microstructure[C] //46th AIAA Aerospace Sciences Meeting and Exhibit, Aerospace Sciences Meetings, Reno, Nevada, AIAA 2013-558,2013.
[12] Fedorov A, Kozlov V, Addison R.Reflection of acoustic disturbances from a porous coating of regular microstructure[C] //5th AIAA Theoretical Fluid Mechanics Conference,Fluid Dynamics and Co-located Conferences, Seattle, Washington.AIAA 2008-3902,2008.
[13] Fedorov A.Temporal stability of hypersonic boundary layer on porous wall: comparison of theory with DNS[C] //48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Aerospace Sciences Meetings,Orlando, Florida,AIAA 2010-1245, 2010.
[14] Fedorov, A V.Prediction and control of laminar-turbulent transition in high-speed boundary-layer flows[J].Procedia Iutam, 2015, 14:3-14.
[15] Brès G A, ColoniusT, Fedorov A.Interaction of acoustic disturbances with micro-cavities for ultrasonic absorptive coatings[C] //5th AIAA Theoretical Fluid Mechanics Conference,Fluid Dynamics and Co-located Conferences,Seattle, Washington, AIAA-2008-3903,2008.
[16] Bres G, Colonius T, Fedorov A.Stability of temporally evolving supersonic boundary layers over micro-cavities for ultrasonic absorptive coatings[C] //5th AIAA Theoretical Fluid Mechanics Conference,Fluid Dynamics and Co-located Conferences,Seattle, Washington, AIAA-2008-4337, 2013.
[17] Brès G, Colonius T.Three-dimensional instabilities of compressible flow over open cavities[J].Journal of Fluid Mechanics, 2008, 599:309-339.
[18] Brès G, Inkman M, Colonius T, et al.Alternate designs of ultrasonic absorptive coatings for hypersonic boundary layer control[C] //39th AIAA Fluid Dynamics Conference, Fluid Dynamics and Co-located Conferences, San Antonio, Texas,AIAA 2006-4217,2006.
[19] Brès G A, Colonius T, Fedorov A V.Acoustic properties of porous coatings for hypersonic boundary-layer control[ J].AIAA Journal, 2010, 48(2):267-274.
[20] Brès G A, Matthew I, Tim C, et al.Second-mode attenuation and cancellation by porous coatings in a high-speed boundary layer[J].Journal of Fluid Mechanics, 2013, 726:312-337.
[21] Lv P,Yu C,Zhang Y,et al.Numerical investigation of ultrasonically absorptive coating for hypersonic laminar flow control[C] //21st AIAA International Space Planes and Hypersonics Technologies Conference.2017:2311.
[22] Malik M R.Numerical methods for hypersonic boundary layer stability[J].Journal of Computational Physics, 1990, 86(2): 376-413.
[23] Anderson J D.Hypersonic and High-temperature Gas Dynamics[M].AIAA Education Series, 2006: 287-306.
[24] Sandham N D, Ludeke H.Numerical study of Mach 6 boundary-layer stabilization by means of a porous surface[J].AIAA Journal, 2009, 47(9): 2243-2252.
[25] Van Driest E R.Investigation of laminar boundary layer in compressible fluids using the crocco method[R].NACA Technical Note 2597,1952.

