“母题”的拓展应用——以“竖直平面内的圆周运动”为例

赵军年

（甘肃省武威第六中学）

随着逐年、各地高考对学生能力要求的变化，由高考衍生出的新颖题目越来越多，就像物理概念中的“熵”一样一直在增加，而对于高中阶段同时具有多门学习任务的学生来说，确实是应接不暇，尤其是高三的学生真的难以应对，那么如何让学生从题海中跳出来，让学生既能轻松应对高考，又能很好地掌握知识提升能力呢？掌握母题解法规律，研究母题拓展，可瘦身高考题典，使学生举一反三，触类旁通，让学生快乐学习，轻松备考，事半功倍。掌握了母题就掌握了所有题目的骨架，如果学会了母体拓展就具备了驾驭高考试题的能力。下面以“竖直平面内的圆周运动”为例来探讨母题的拓展应用。

例题 如图1所示，一根长为L的轻质细线（不可伸长）一端固在O点，另一端系一个质量为m的小球（可看成质点），现给小球一水平向右的初速度v0，重力加速度为g。

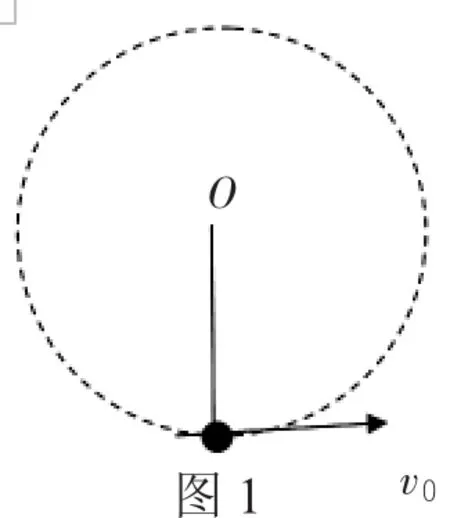
图1

（1）v0是多少时，小球在竖直平面内恰好做完整的圆周运动？

（2）若让小球在竖直平面内运动而让轻绳一直不松弛，应满足什么样的条件？

解析

图2

（1）若想让小球在竖直平面内恰好做完整的圆周运动，则要求小球既不能做近心运动也不能做离心运动，题目中未要求轻绳的最大拉力，所以不考虑离心运动。当小球通过圆心所在水平面以上高度时，如图2以D点为例，对小球受力分析，由向心力公式得，由机械能守恒知，小球越往上走速度越小，随着θ减小，cosθ在增大，mgcosθ就越大，绳子的拉力就越小，小球刚好脱离轨道时绳子的拉力为零，当给小球提供的向心力大于需要的向心力时，即时，小球会做近心运动而让轻绳松弛脱离轨道，小球越往上走越容易使得 F提供的向心力>F需要的向心力，当小球运动到最顶端C时，速度最小，重力的分力最大，所以要想让小球在竖直平面内恰好做完整的圆周运动，就一定得过最高点C。

设小球通过最高点C的最小速度为vmin，此时轻绳拉力恰好为零，由圆周运动的向心力得

小球从A到C的过程应用动能定理得：

可知要使小球在竖直平面内恰好做完整的圆周运动，小球应满足

图3

设小球恰能运动到图3中的B点（速度为零），在A到B的过程中应用动能定理得：

综上所述，若让小球在竖直平面内运动而让轻绳一直不松弛，有以下两种情况：

拓展应用一：

若将上题中的轻绳去掉，改为竖直光滑圆弧轨道，让小球在其内测运动而不脱离轨道，则小球在最低点的速度v0应满足什么条件？

思维启迪：小球为研究对象受力分析，发现小球所受圆轨道的支持力和（2）问中的轻绳的拉力作用效果是相同的，所以上面（2）问中的结论也是小球在竖直光滑圆轨道上运动而不脱离轨道的条件，即或者

结论：轻绳拉小球模型和小球在光滑圆弧轨道的内侧运动遵循相同的规律。

拓展应用二：

思维启迪：因为轻绳拉小球模型和小球在光滑圆弧轨道的内侧运动遵循相同的规律。题目所给小球速度大于如图4所示，小球能越过圆心所在水平面的B点，而v0小于小球不能到达圆弧最高点，小球在BC之间某一位置会脱离圆弧轨道，设脱离位置为F点，速度为VF，小球在脱离圆弧轨道时，轨道对小球的弹力N为零，脱离轨道后小球将做斜上抛运动，由斜上抛规律知小球在最高点的速度是vFcosθ。

图4

在图4中的F点对小球受力分析（轨道对小球的弹力N为零），由圆周运动的向心力得

小球从A点运动到F点应用动能定理得

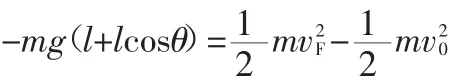
拓展应用三：

若将轻绳改为轻杆后，其他条件不变，让小球在竖直平面内做完整的圆周运动，v0应满足什么样的条件？

思维启迪：若改为轻杆，小球在轻杆的约束下不可能做近心或离心运动，小球在沿着圆弧向上运动过程中，速度越来越小，如上图4所示，只要过最高点C，小球就能做完整的圆周运动。

如图4所示，假设小球恰能运动到最高点C（此时小球速度为零），对小球从A点到C点的过程，应用动能定理得：

拓展应用四：

如图5所示，一半径为R的光滑球体固定在水平地面上，一小球（可看成质点）受轻微扰动从球面的顶端无初速滑下，小球的质量为m，重力加速度为g，问：小球在球面上何位置脱离？

图5

思维启迪：小球在沿球面下滑过程中做圆周运动，由机械能守恒得小球的速度越来越大，需要的向心力也越来越大，而重力的分力mgcosθ和球面的支持力的合力提供向心力，即（mgcosθ-N）提供向心力，小球下滑过程中θ在增大，cosθ在减小，而提供的向心力却要求增大（因提供的向心力等于需要的向心力），这样球面的支持力就越来越小，直到为零（此时刻小球刚好要脱离球面）。

设小球恰好在位置脱离球面，脱离时的速度是v，在点受力分析并由向心力公式得：

从O点到点应用动能定理得

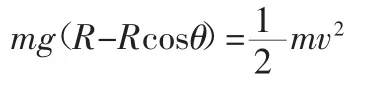
结论：轻杆模型和小球在弧形轨道的外侧运动也遵循相同的规律。

参考文献：

［1］董海燕.什么地方容易脱轨［J］.中学物理，2008（7）：57-58.

［2］杨榕楠.更高更妙的物理［M］.杭州：浙江大学出版社，2015:77-81.