预应力碳纤维布加固型钢梁变形计算分析

龚田牛 吴 涛

(1.湖北文理学院土木工程与建筑学院,襄阳 441053; 2.武汉大学土木建筑工程学院,武汉 430072)

0 引 言

随着国民经济的发展,钢结构在工业与民用建筑中的应用范围越来越广,钢结构在服役过程中,当存在损伤和使用条件改变时,应对钢结构进行补强加固[1]。钢结构的常用加固方法主要包括焊接、铆接、粘钢加固法和粘贴碳纤维布加固法[2-6]。其中,粘贴碳纤维布加固技术由于碳纤维布的抗拉强度高、自重轻、耐磨性和耐老化性好以及施工方便、施工质量易于保证等优点而逐步发展成为工程结构加固补强中的一种主要加固技术[7-10],但碳纤维布厚度很薄,其弹性模量和钢材相近,直接用于钢梁加固时碳纤维布的强度要在钢材屈服后才得以发挥,加固效果不是十分明显[11-12]。因此,以预应力碳纤维布加固钢筋混凝土梁为基础[13-14],将碳纤维布进行预张拉后再用于钢梁加固,不仅提高了钢梁的抗弯承载力,其刚度也得到提高,变形得以控制[15]。本文在试验研究基础上,对比了不同加固方式下型钢梁的刚度和承载力,对预应力碳纤维布加固型钢梁的挠度曲线方程进行了分析,并根据不同阶段提出了预应力碳纤维布加固型钢梁在型钢梁屈服前和屈服后的挠度计算方法。

1 试验概况

1.1 试件设计

本次试验共设计7根试件。以I14工字形型钢梁为研究对象,实测屈服强度和抗拉强度分别为255 MPa、376 MPa,弹性模量为208 GPa。碳纤维布采用UT70-20型布,通过材性试验测得抗拉强度为4 363 MPa,弹性模量为249 GPa,碳纤维布和钢材的弹性模量相近。试件分为未加固型钢梁、碳纤维布加固型钢梁和预应力碳纤维布加固型钢梁,试验参数包括加固方式、碳纤维布层数和碳纤维布预拉力值。试件加载模型如图1所示。试验梁两端简支跨度为1 300 mm,采用两点加载,两个集中力加载点的距离为400 mm,碳纤维布加固长度为1 000 mm,采用预应力碳纤维布加固时在端部设置永久锚具。试件的分组情况如表1所示。

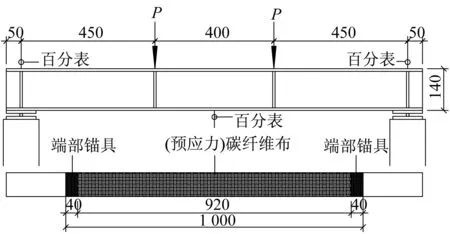
图1 试件加载示意图(单位:mm)Fig.1 General view of test setup (Unit:mm)

表1试件分组表

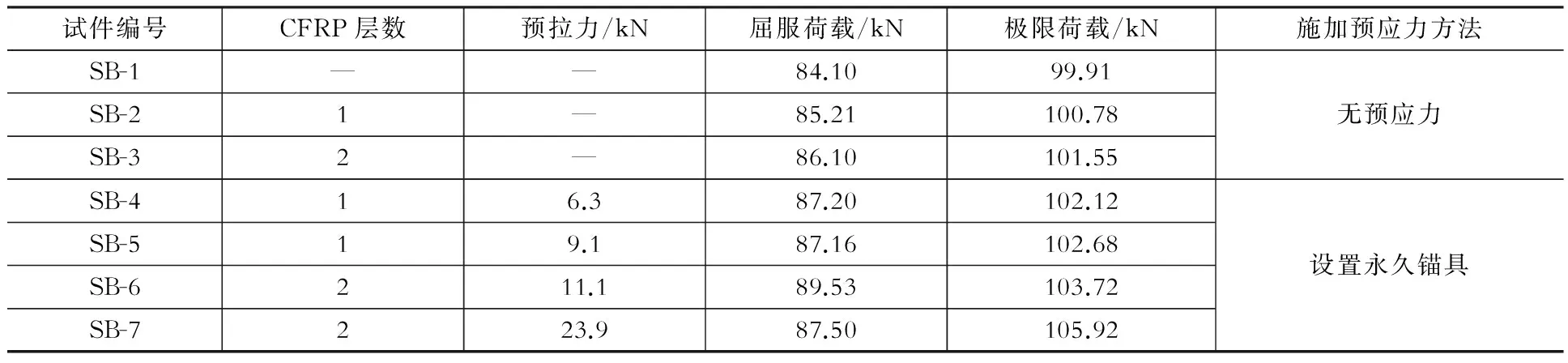
Table 1 Detail of the specimens

1.2 试验结果分析

所有加固梁的试验现象基本一致:屈服荷载以前,随着荷载的增大,挠度不断变大,两者基本为线性关系;随着荷载的继续增加,挠度的增长速度变快,钢梁进入塑性阶段;达到极限荷载后继续加载,碳纤维布端部部分被拉断,整个加载过程中,没有出现失稳现象。试验梁的屈服荷载和极限荷载见表1,相应的荷载-挠度曲线如图2所示。可以看出,相对于未加固梁,非预应力碳纤维布加固梁的屈服荷载及刚度提高不明显,而对于预应力碳纤维布加固梁,屈服荷载和极限荷载均有不同程度的提高,且随碳纤维布层数的增加而增大。其中,相对于试件SB-1,预应力碳纤维加固的试件SB-4至SB-7屈服弯矩提高幅度为5.1%～7.1%,极限弯矩提高幅度最大为11%。

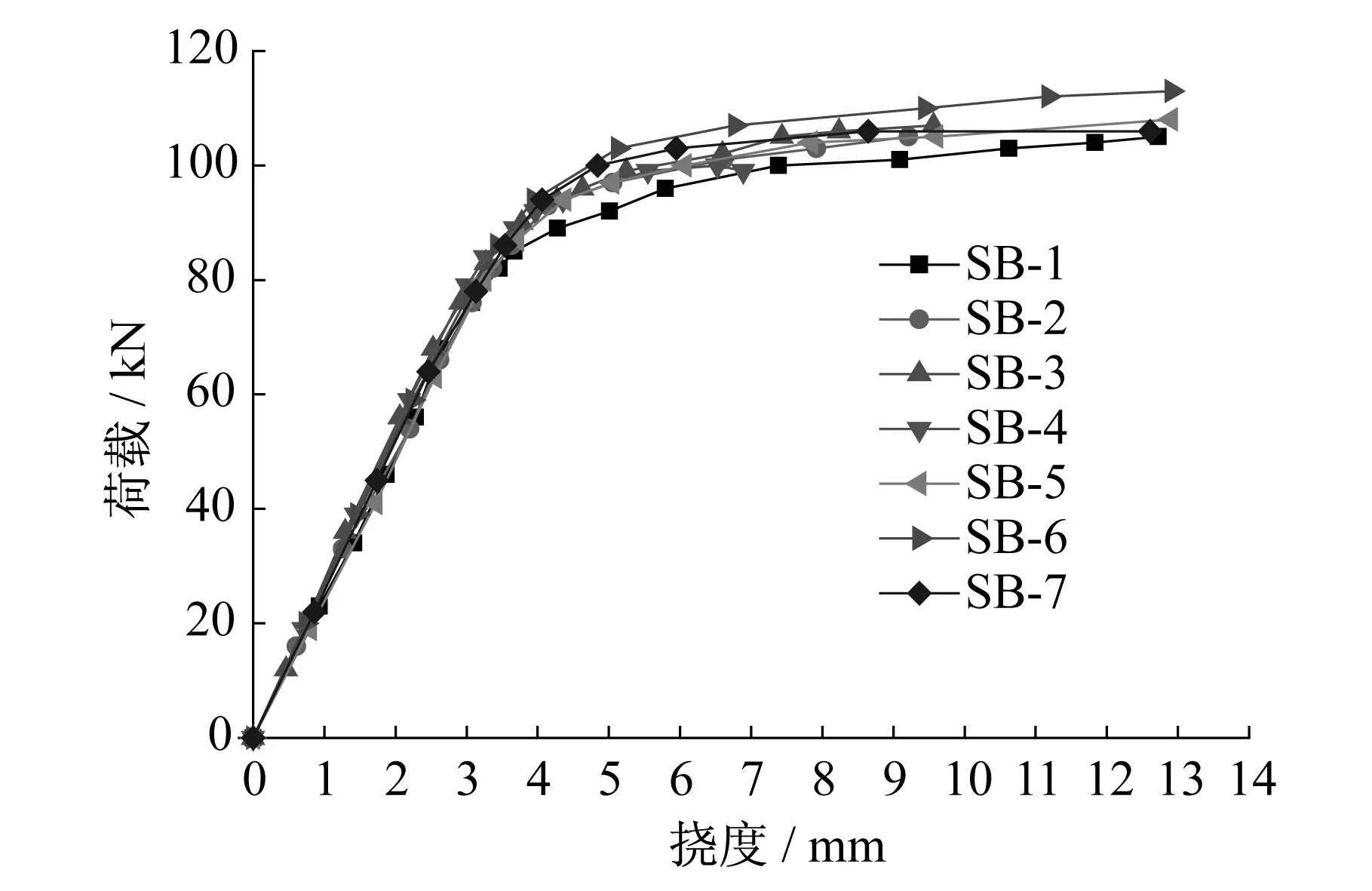
图2 试件荷载-挠度曲线Fig.2 Loading-deflection curves of specimens

2 变形分析与计算

2.1 预应力碳纤维布加固型钢梁的挠度变化特点

从图2可以看出,预应力碳纤维布加固型钢梁的刚度变化主要分为两个阶段:①弹性阶段。此阶段为直线,由于碳纤维布的弹性模量和钢材相近,且碳纤维布层数较少,与未加固型钢梁相比,预应力碳纤维布加固型钢梁的直线斜率有不同程度增加,但增加不显著。②屈服至破坏阶段。继续加载,型钢梁最外侧纤维达到钢材的屈服强度,试验梁的荷载-挠度曲线斜率减小,碳纤维布的应力急剧增大,对型钢梁的变形起到了较强的约束作用,碳纤维布的作用逐渐被发挥出来,预应力碳纤维布加固型钢梁的刚度提高较明显。根据上面两个不同的阶段,可以分析试验梁相应的变形。

2.2 预应力碳纤维布加固型钢梁屈服前挠度分析

当试验梁在弹性范围内时,曲率κ与弯矩成正比,挠度曲线近似微分方程为

(1)

对预应力碳纤维布加固型钢梁,在荷载作用下,其挠度由两部分组成[16]:一部分为使用荷载产生的挠度v1;另一部分为预应力产生的反拱v2。因此,试验梁的最终挠度v为

v=v1-v2

(2)

对于外荷载产生的挠度v1,在试验梁屈服前可以用弹性理论来建立截面参数,各试验梁的中性轴高度y0为

(3)

式中,As,Acf分别为型钢梁和碳纤维布的截面面积;y1,y2分别为型钢梁和碳纤维布截面形心至参考轴距离。

ηbtcf·(h+tcf-y0-0.5tcf)2

(4)

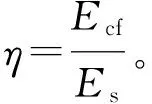
在得到了试验梁截面的抗弯刚度后,便可按材料力学中给出的集中荷载作用下梁的位移公式计算变形v1。对本文的简支梁而言,其挠度曲线方程为

(5)

式中,P为所加荷载大小;l为试验梁跨度;x为支座至跨中的距离;b1,b2分别为集中荷载至支座距离。

对于预应力作用下产生的反拱v2,可根据预应力的作用,由图乘法计算出来。本文中预应力作用下的反拱为

(6)

式中,Tcf为对碳纤维布施加的预应力值;e为碳纤维布合力作用点至等效截面的形心轴距离。

由式(2)-式(6)可算出试验梁的挠度值,并与试验结果相比较,其结果见表2。

表2试验梁屈服前挠度计算值与试验值对比

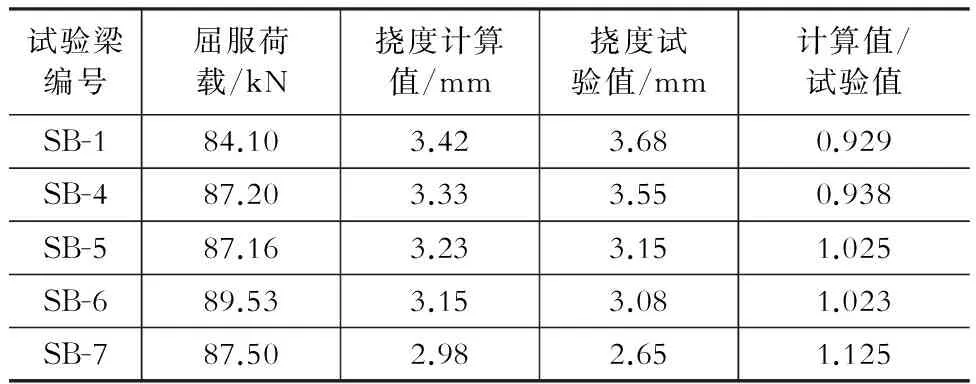
Table 2 Comparison between theoretical and experimental results of deflection before yield

挠度计算值与试验值比值的平均值为1.008,均方差为0.079,计算结果与试验结果吻合较好。

2.3 预应力碳纤维布加固型钢梁屈服后挠度分析

当试验梁进入弹塑性阶段后,截面的曲率κ不再与弯矩成正比,此时截面曲率κ为[17]

(7)

通过积分法以及边界条件可得到试验梁中各点的挠度值v,v的表达式如下(仅考虑弯曲变形):

(8)

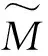
对承受两集中力的简支梁,假设试验梁的纯弯段出现塑性,且此时试验梁截面中央的弹性核高度为αh,则该截面的弯矩为

M=γ0My

(9)

式中,My为试验梁屈服弯矩;γ0为试验梁纯弯段截面的塑性发展系数(对应α取α0),其计算公式为[17]

(10)

式中,γF为截面形状系数;h0为腹板高度;b,h为型钢梁的宽度和高度;t为翼缘厚度;Wnx为型钢梁弹性抗弯模量。

试验梁计算简图如图3所示,由力学分析可知:

(11)

Mx=Px0≤x≤a

(12)

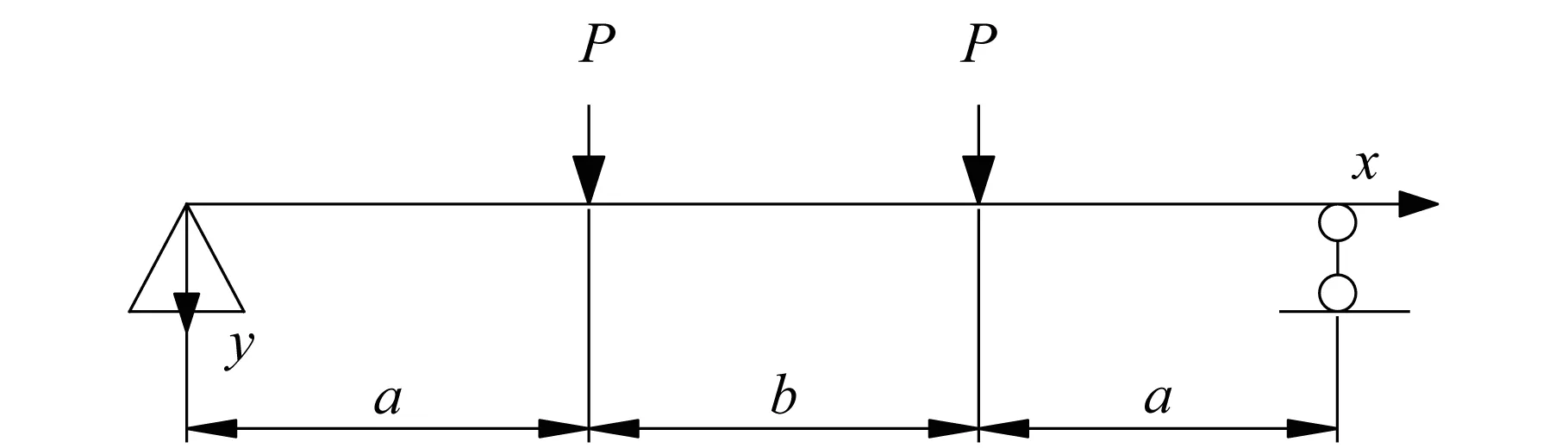
图3 试验梁计算简图Fig.3 Calculation chart of the specimens

(13)

先由式(9)-式(12)可以得到γ关于横坐标x的函数,然后再用此γ替换式(10)中的γ,同时进行反函数运算,就可得到α关于x的函数式。

当采用连续二次积分法求试验梁的挠度时[18],计算公式如下:

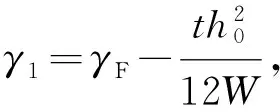
(14)

(2) 当h0≤α0h≤h时,即考虑纯弯段截面塑性发展较少时,试验梁轴线转角曲线y′的表达式为:

(15)

则试验梁的挠度曲线y的表达式为

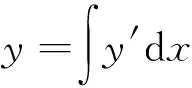
(16)

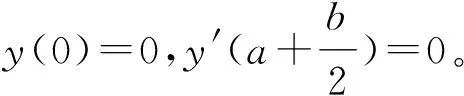
y(a)-=y(a)+,y′(a)-=y′(a)+

这时,便可求得试验梁在荷载作用下跨中的挠度:

(17)

采用虚功法求跨中挠度,计算公式按式(8)选取,计算时仍然可利用试验梁的对称性来简化计算,同样也分0≤α0h≤h0和h0≤α0h≤h这两种情况。

对于预应力碳纤维布加固试验梁,当在荷载作用下试验梁进入屈服阶段后,其挠度仍然由两部分组成:一部分为使用荷载产生的挠度,其值可按式(17)来计算,另一部分为预应力产生的反拱,其值可按式(3)来计算。则试验梁最终的跨中挠度v′为

v′=vm-v2

(18)

根据式(18)可计算出试验梁屈服后的挠度值,由于试验中大部分试验梁以跨中挠度达到1/200L时的承载力为极限承载力,而试验梁的真实极限承载力还未达到,为此未列出屈服后挠度计算值与试验值的对比。

3 结 论

(1) 对于非预应力碳纤维布加固的型钢梁,其屈服荷载以及屈服前刚度的提高并不明显,碳纤维布的强度在型钢梁屈服前得不到发挥,利用率较低。利用预应力碳纤维布加固型钢梁可以使碳纤维布提前参与工作,从而提高了碳纤维布的利用率,并提高了被加固型钢梁的屈服荷载和刚度,取得了较好的加固效果。

(2) 在试验研究的基础上,对预应力碳纤维布加固型钢梁的变形进行了分析,并分成弹性阶段和屈服至破坏阶段,提出了预应力碳纤维布加固型钢梁屈服前挠度计算公式,计算结果与试验结果吻合较好,从理论上推导出预应力碳纤维布加固型钢梁屈服后挠度计算方法,可为实际工程应用提供参考。

[1] 程江敏,程波,邱鹤,等.钢结构加固方法研究进展[J]钢结构,2012,27(11):1-6.

Cheng Jiangmin,Cheng Bo,Qiu He,et al.Research of development of steel structure reinforcement[J].Steel Construction,2012,27(11):1-6.

[2] Tall L.The reinforcement of steelcolumns[J].Engineering Journal,American Institute of Steel construction,1989,26(1):33-37.

[3] Liu Y,Gannon L.Experimental behavior and strength of steel beams strengthened while under load[J].Journal of Constructional Steel Research,2009,65(6):1346-1354.

[4] Liu Y,Gannon L.Finite element study of steel beams reinforced while under load[J].Engineering Structures,2009,31(11):2630-2642.

[5] 王元清,祝瑞祥,戴国欣,等.工字型截面受弯型钢梁负载下焊接加固试验研究[J].土木工程学报,2015,48(1):1-10.

Wang Yuanqing,Zhu Ruixiang,Dai Guoxin,et al.Experimental study on bending steel beams with I section strengthened by welding under initial load[J].China Civil Engineering Journal,2015,48(1):1-10.

[6] 祝瑞祥,王元清,戴国欣,等.负载下钢结构构件增大截面加固设计方法对比分析[J].四川建筑科学研究,2014,40(1):98-103.

Zhu Ruixiang,Wang Yuanqing,Dai Guoxin,et al.Comparative study on design methods for steel structural members strengthened by increasing the section area while under load in different codes [J].Sichuan Building Science,2014,40(1):98-103.

[7] 卢亦焱,黄银燊,张号军,等.FRP加固技术研究新进展[J].中国铁道科学,2014,40(1):98-103.

Lu Yiyan,Huang Yinshen,Zhang Haojun,et al.New progress in the study of the technology of reinforcement with fiber reinforced plastics[J].China Railway Science,2014,40(1):98-103.

[8] Bocciarelli,Massimiliano,Colombi Pierluigi,et al.Fatigue performance of tensile steel members strengthened with CFRP plates[J].Composite Structures,2009,87(4):334-343.

[9] Bambach M R,Elchalakani M.Plastic mechanism analysis of steel SHS strengthened with CFRP under large axial deformation thin-walled structures,2007,45(2):159-170.

[10] Shaat Amr,Fam Amir.Slender steel columns strengthened using high-modulus CFRP plates for buckling control[J].Journal of Composites for Construction,2009,13(1):2-12.

[11] 彭福明,郝际平.碳纤维增强复合材料(CFRP)加固修复损伤钢结构[J].工业建筑,2003,33(9):7-10.

Peng Fuming,Hao Jiping.CFRP for strengthening and repairing of damaged steel structure[J].Industrial Construction,2003,33(9):7-10.

[12] 马建勋.粘贴碳纤维布加固钢构件受拉承载力试验研究[J].工业建筑,2003,33(2):1-4.

Ma Jianxun.Experimental study on tensile behavior of steel member strengthened by CFRP sheet[J].Industrial Construction,2003,33(2):1-4.

[13] Garden H N,Hollaway.An Experimental Study of the strengthening of reinforced concrete beams using prestressed carbon composite plates[C]//Proceeding of the 7th international conference on Extending the life of Bridge,1997:191-199.

[14] Triantafillou,Deskovic.Strengthening of concrete structure with prestressed fiber reinforced plastic sheets [J].ACI Structural Journal,1992,89(3):235-244.

[15] 卢亦焱,龚田牛,李杉,等.预应力碳纤维布加固型钢梁抗弯承载力研究[J].铁道学报,2013,35(6):104-109.

Lu Yiyan,Gong Tianniu,Li Shan.Analysis of flexuralstrength of steel beams strengthened with prestressed carbon fiber reinforced polymer (CFRP) [J].Journal of the China Railway Society,2013,35(6):104-109.

[16] 林同炎.预应力混凝土结构设计[M].北京:中国铁道出版社,1983.

[17] 陈绍藩.钢结构设计原理[M].北京:科学出版社,2003.

[18] 王文炜,赵国藩.玻璃纤维布加固的钢筋混凝上梁挠度计算[J].四川建筑科学研究,2004,30(3):3-36.

Wang Wenwei,Zhao Guofan.Calculation of deflection of RC beams strengthened with GFRP sheets[J].Sichuan Building Science,2004,30(3):3-36.