基于Matlab的桩锚支护结构优化设计

赵 洪，张君仁

（山西大同大学建筑与测绘工程学院，山西大同037003）

随着我国经济的发展，城市规模不断扩大，高层建筑大量兴建，建筑高度不断加大，基坑深度不断加深，使得基坑在开挖和支护过程中发生事故的概率大大增加。一方面，为了保证工程的安全，支护结构的设计往往非常保守，造成资源的不必要浪费；另一方面，由于支护结构的临时性，一旦基础施工完成，其作用也就消失了，因而在支护上的投入较少，有时为了片面追求经济效益，不惜以降低基坑的变形、稳定性和安全方面的要求，造成工程事故的发生，导致了更大的经济损失[1-3]。为了实现既经济又安全，达到质量和成本最大程度上的统一，加强基坑支护优化设计及数值模拟研究、提高基坑工程实践指导的科学性是解决这一问题的关键。

1 Matlab简介

美国MathWorks公司于1984年将Matlab推向市场，可靠的数值计算和符号计算功能、强大的绘图功能、简单易学的语言体系以及为数众多的应用工具箱是Matlab区别于其他科技应用软件的显著标志[4]。

Matlab以矩阵作为数据操作的基本单位，这使得矩阵运算变得非常简捷方便高效。Matlab还提供了十分丰富的数值计算函数，而且所采用的数值计算方法都是国际公认的最先进、可靠的算法，其程序由世界一流专家编制和高度优化。将Matlab提供的优化算法用于基坑支护方案的选择过程中，从而优选出一个最佳方案。

2 优化模型

2.1 设计变量的选取

在桩锚支护结构的优化设计中，可共选择的变量非常多。依据设计变量的选取原则[5]，对目标函数值影响大、并且一般设计者很难掌握得比较准确的那些设计参数，应选作优化设计过程中的设计变量。而对于那些可以根据相关的规范、标准、地质条件等确定的参数，或者凭借设计者的经验或区域经验就能确定的参数作为已知参量预先固定下来。

根据上述原则，选取桩的配筋面积As、桩径d、桩间距S、嵌固深度hd及锚杆间距S、锚杆钻孔直径D、锚杆层数n、锚杆深度mn、锚杆倾角θ、自由段长度Lf、锚固段长度La作为设计变量[6]，由编制的Matlab程序自动求得最优解。

2.2 目标函数的建立

优化设计的目标是使总造价为最小[7-9]。本文桩锚支护方案取支护桩和锚杆造价作为目标函数，以1 m3的混凝土价格为1，则目标函数F为：

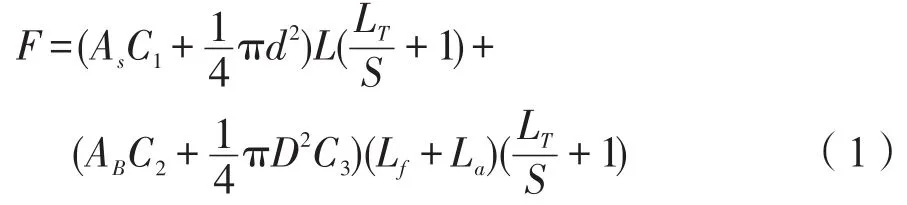
式中：As为桩配筋面积；C1为支护桩每立方米钢筋与混凝土价格比；d为桩径；L为桩长；LT为需要护坡的基坑长度；S为桩间距及锚杆间距；AB为预应力筋截面积；C2为锚杆每立方米钢绞线与混凝土价格比；D为锚杆钻孔直径；C3为锚杆钻孔每立方米水泥浆与混凝土价格比；Lf为自由段长度；La为锚固段长度。

2.3 约束条件[10-11]

为了使支护结构能够满足强度、变形和稳定性的要求，必须满足一定的约束条件。

2.3.1 设计变量约束

（1）桩配筋面积As：

式中：K为配筋安全系数；M为桩的最大弯矩；αt=1.25-α。

（2）桩径d：0.4≤d≤1.8。

（3）桩距S：1.2d≤S≤2.5d。

（4）嵌固深度hd：0.2h≤hd≤1.5h。

（5）锚杆设置深度：锚固段的上覆土层厚度≥4m，首道支撑位置m1：0＜m1＜h(调整后为2＜m1＜h)，其余支撑位置mn：mn-1＜mn＜h。

（6）锚杆水平间距S：≥2 m。

（7）锚杆倾角θ：10°≤θ≤45°。

（8）锚杆钻孔直径D：0.075≤D≤0.15。

（9）锚杆长度：

自由段长度Lf：Lf≥5，且

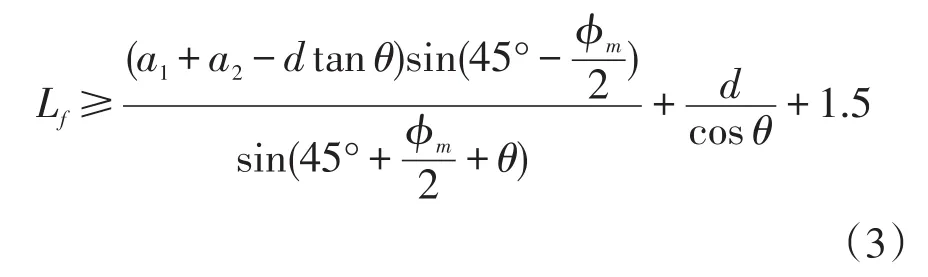
式中：a1为锚杆的锚头中点至基坑底面的距离；a2为基坑底面至基坑外侧主动土压力强度与基坑内侧被动土压力强度等值点的距离；φm为强度等值点以上各土层按厚度加权的等效内摩擦角。

锚固段长度La：4≤La≤40。

2.3.2 设计准则约束

（1）锚杆上覆土层厚度应符合下式要求：

根据岩土工程勘察报告的场地地层信息，大部分场区首层土为填土，其物理力学性质较差，因此将首层锚杆的埋深m1调整为2＜m1＜h，采用经调整后的支撑位置约束条件后，在优化设计时，可以忽略锚杆上覆土层的厚度验算。

（2）锚杆的极限抗拔承载力应符合下式要求：

式中：Kt为锚杆抗拔安全系数，安全等级为一级、二级、三级的支护机构，分别不应小于1.8、1.6和1.4；Rk为锚杆极限抗拔承载力标准值，通过抗拔试验确定，或根据（6）式估算；Nk锚杆轴向拉力标准值，按（7）式计算。

（3）第K层支撑设置后，围护结构的嵌固深度应满足下式要求：

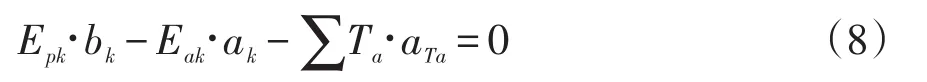
据此原理，计算设计嵌固深度约束为：

式中：d为基坑开挖面以下土压力为零点深度；k为安全系数，一、二、三级基坑分别取1.4、1.3、1.2；l为土压力为零点深度以下需要的桩的长度，计算公式为

因此，桩的嵌固深度hd≥Hd。

3 算例

某基坑深9.2 m，东侧距离坑边1.5 m为一住宅小区的围墙，围墙继续向东6.5 m为一栋7层住宅楼，在围墙内东南角有一幢二层砖混结构的综合楼，一楼为商店，二楼为游乐场，为保证在基坑施工过程已有建筑的安全和正常使用，该侧采用桩锚支护结构设计方案。场区地层主要为粉土和粉质粘土，场地土层分布及其物理力学指标，见表1。

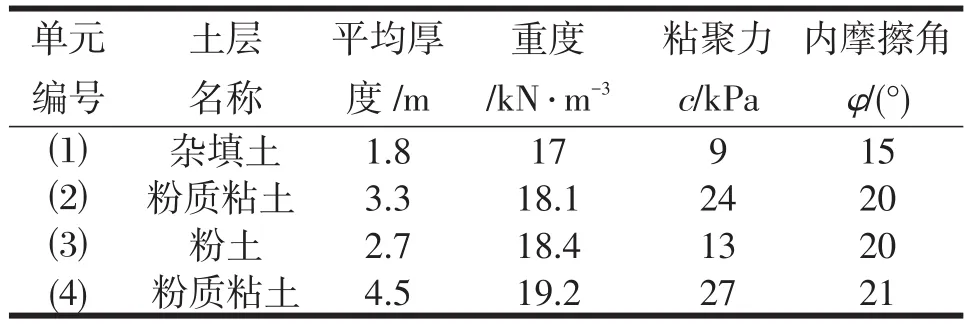
表1 基坑深度范围内各土层物理力学参数

根据前述的桩锚支护优化设计理论，编写Mat⁃lab优化设计程序，程序中以1 m3的混凝土价格为1，水泥砂浆与混凝土的价格比为1∶1，钢筋与混凝土的价格比为80∶1，其优化设计结果与原设计成果对比，见表2。

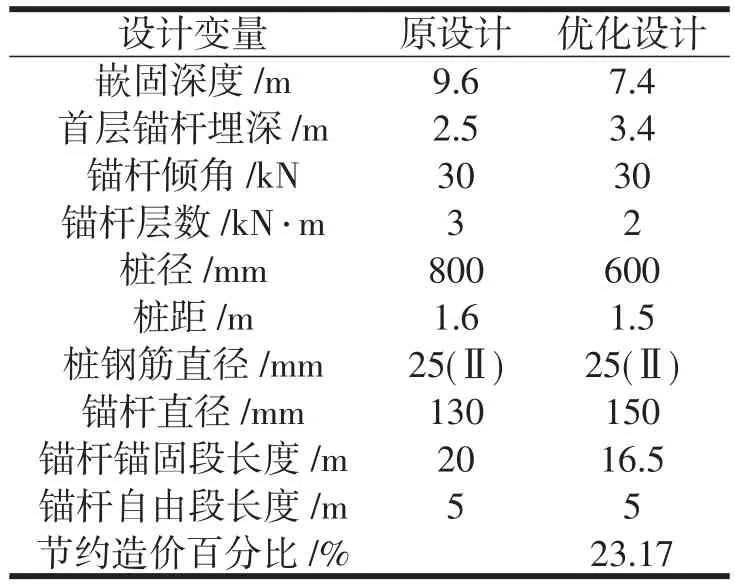
表2 优化设计结果与原设计的对比

由表2知，经优化设计后，比原设计节约23%的资金。

4 结论

（1）优化模型包括选取设计变量、建立目标函数和确定约束条件三方面内容。

（2）选取在设计中不易被掌握的且对目标函数值影响大的参数作为设计变量；取支护桩和锚杆造价作为目标函数，使造价最低并满足设计变量约束和设计准则约束。

（3）将优化设计编写成Matlab程序得出优化设计结果，并将该优化设计方案与原设计方案进行比较，优化设计比原设计方案节约造价23%。

因此，基于Matlab的基坑支护优化设计具有可行性和较高的实践价值。

[1]王一鸣.深基坑多支点桩锚支护结构优化设计[D].兰州:兰州理工大学,2014.

[2]冯少杰,伏永贵,邱浩然，等.基于豆石混凝土的异型锚杆承载力试验研究[J].科学技术与工程,2016,16(29):302-305.

[3]丁书学,靖洪文,孟波,等.地应力作用下裂隙对锚杆预应力扩散机制的影响[J].科学技术与工程,2017,17(17):192-200.

[4]寇永照.管棚支护参数优化及计算程序设计[D].西安:西安科技大学,2012.

[5]吴恒,李陶深,韦日钰,等.遗传算法在深基坑支护工程优化设计中的应用[J].广西大学学报,2003,25(1):1-4.

[6]袁彬.深基坑支护方案优选与优化设计研究[D].淮南:安徽理工大学,2008.

[7]徐洪泉,罗海亮,李春生,等.基于遗传算法的深基坑桩锚支护结构的设计优化与MATLAB实现[J].公路工程,2012,37(3):158-161.

[8]詹建华.基于Matlab的深基坑优化设计理论与应用研究[D].武汉:武汉理工大学,2005.

[9]翁杰,谭跃虎,金丰年.基于Matlab的基坑支护优化设计[J].解放军理工大学学报（自然科学版）,2004,5(3):63-66.

[10]中华人民共和国住房和城乡建设部.建筑地基基础设计规范:GB50007—2011[S].北京:中国建筑工业出版社,2012.

[11]中华人民共和国住房和城乡建设部.建筑基坑支护技术规程:JGJ120—2012[S].北京:中国建筑工业出版社,2012.