在知识“流通”过程中培养数学核心素养
陈 云

培养好的数学核心素养,我们需要改变“获取知识就是为了储存”的现象,把“接收”、“储存”知识的过程转变为知识的“流通”过程。实现知识的“流通”,学生需要在查验“原储存”的过程中产生问题,再按自己的方式提取认为有用的“原储存”来弥补解决新问题的空白点,然后通过反复试验、反思、改进和完善,让认知得以发展。从查验原有知识到产生新的问题;从提取有效证据到解决新的问题;从探究实验到获取新的认知,整个“流通”过程中学生需要解决“是什么?”“为什么?”“怎么解决?”这样的问题,变“一听就明白”为“真正搞明白”,这样才能更好地培养学生的数学核心素养。
一、活动“支架”促进知识“流通”
任何的学习过程都离不开活动的介入,学生在活动过程中形成的某种体验或方法性知识会在其遇到某种相似情境时被忆起,这就是我们所说的数学活动经验。教学中,我们需要设计出平行发展(或层层递进)的数学活动,以活动为“支架”,在活动参与中学生会不着痕迹地“解冻”原有的经验、反思新的问题、寻找新的办法、完善新的认知,这就实现了知识的“流通”,避免单方向的“接收”和“储存”。例如,在北师大版教材二年级下册第三单元《生活中的大数》第四课“比一比”教学中,学生有了百以内数比较大小的经验,对于较大数比较大小的方法完全可以在合适的数学活动中自主获得。教学中,我放弃了教材给予的素材,没有使用几个“冷冰冰”的数据,而是设计了层层递进的三个“比输赢”小游戏。
游戏1:男、女生各派1名代表抽签,每组抽三次,抽到的数字从个位开始依次摆放,摆出的数大的小组赢。你能快速确定输赢吗?
反思:为什么一定要到游戏结束时才能定输赢?
追问:规则不变,接着抽下去,怎样确定输赢?
游戏2:男、女生各派1名代表抽签,每组抽四次,抽到的数字从千位开始依次摆放,摆出的数大的小组赢。你能快速确定输赢吗?
讨论:为什么这次抽一个数字你就能确定输赢了呢?
追问:假如第一次抽到的数字一样大,怎样定输赢?
游戏3:男、女生各派1名代表抽签,每组抽四次,抽到的数字自己决定放在哪一位上,摆出的数大的小组赢。你能快速确定输赢吗?
交流:现在要如何才能确定谁输谁赢呢?
追问:每次抽到的数字怎样摆放赢的机会更大?
游戏结束后,学生在回顾比赛的全过程中就可以很好地获得比较数的大小的方法,这就把“老师用规范语言进行方法阐述”的“接受”过程转变为学生“解冻原经验、获得新体验”的“流通”过程。在这样的过程中,课堂由“传递中心”走向“对话中心”,学生在游戏的过程中,与客观世界对话、与他人对话、与自己对话,在活动中反思、在合作中思考,这正是我们要培养的数学核心素养。
二、化繁为简实现知识“流通”
不少数学教师热衷于“口诀”的提炼、“方法”的总结、“要素”的概括,这些所谓的要诀,看似简洁,颇得要领,其实很多时候只是我们成人的偏好,学生对之却总是不得要领,所以,我们经常听到老师们抱怨:“我都讲得这么简单了,学生怎么还是不会做呢?”这是因为学生是以形象思维为主的,老师抽象概括出的“标准化”语言和方法反而会增加学习难度。其实,真正的要领是需要学生在知识的“流通”过程中自己去化繁为简,真实地参与到探究、创造、协作与问题解决过程中,带着对问题本源意义的探索,才能发展学生的数学核心素养。
例如:北师大版四年级上册《乘法》的教学,我通过“想—找—比”的环节,让学生从“估算、拆算、表算”……这些繁多的办法中,内化出“竖式计算”这一通用的准则。从而彰显人类“化繁为简”的思维文化。
学生看图提出问题后,我让学生自己想办法解决114×21=?学生有了这样的一些算法:①估算:110×20=2200,120×20=2400,114×21 的积比 2200大,比2400小,它在2200与2400之间;……②拆算 :114 ×20=2280,114 ×1=114,2280+114=2394;114×21=114×7×3=798×3=2394;21×100=2100,21×10=210,21×4=84,2100+210+84=2394;……③竖式计算……不同的算法间有无必然的联系?我改变课本表格设置,引导学生找出表格与竖式的联系,实现算理的同化。重点思考:乘法竖式计算要注意什么?
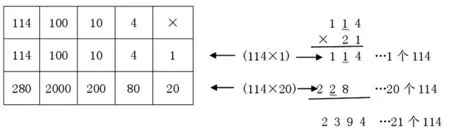
最后让学生自己比繁简:多样的算法中,你认为哪种最简洁?为什么?(估计:能估出范围,但不精确;拆数:能化难为易,但不简洁;列表:能显示算理,但不方便;竖式:不但直观而且通用)既然大家都认可用竖式计算两位数乘法,那我们就用这种办法来完成课本中的“想一想”和“练一练”。
数学知识的学习一定是一个由繁到简、由难到易的过程,作为教师不必急于把自己认为最好的方法告知学生,这样的“好心”往往会办“坏事”,让学生自己去“不怕麻烦”地试一试,或许有一些磕磕绊绊,或许要走一些弯路,但这样的探索一定能唤醒“原储存”的某些经验,并在新问题的解决中逐步同化、顺应,实现知识的“流通”,同时,学生“类比”、“推理”等数学核心素养也得以提升。
三、开放问题助力知识“流通”
很多时候,我们不自觉地以演绎的方式教数学,学生则被动地习得基本知识和基本技能,探究的过程来也匆匆,去也匆匆,学生刚刚走近“洞口”,窥见一丝“光亮”,就被一通直白的宣讲弄得索然无味;或者是“正在嚼着糖果,却被合作交流,探究出糖果的味道”,类似于这样一些追求形式上的“平稳流畅”,怎能激活数学思考?教师不应该仅仅满足于传统意义上的文本的学习,要能够在文本的基础上创设更为开放的问题情境,点燃学生认知的兴奋点,“入一点、牵一线、构一面”,触及学生认知内核,通过问题的开放与教师的统领、学生的独立思考与团队的互动将概念(哪怕是最基本的概念)的建构过程变成一个“意义赋予”的过程,这样才有知识的“流通”,也才有可能帮助学生建构新的认知结构。
例如,学习了“角的度量与画法”,在寻找“角在生活中的应用”时,我给学生提供了这样的情境:风筝比赛中,组织方给每位选手同样长的绳子,待绳子全部放完时,只要测量出绳子与地面形成的夹角就能比较出谁的风筝飞得高了。学生短暂惊讶后小声嘟囔开了:“风筝飞得高低怎么会与角度有关呢?”“不是说角的大小与边的长短无关吗?”……在此起彼伏的质疑声中,我及时组织学生展开探究,实际画一画、量一量,以地平线为角的一条边,以8cm代替相同绳长,分别画出30°、45°、60°角,比一比角的另一边端点所在的高度,学生豁然开朗。紧接着,我带领学生继续寻找生活中这些有趣的角度。比如,足球比赛中,球员为什么要努力把球带到离球门更近的地方才起脚射门?画一画、量一量,球在不同位置时与球门形成的夹角有什么不同,这个夹角会对射门产生什么样的影响?又如,我们坐的小椅子靠背成多少角度才舒服呢?你能设计出舒适的角度吗?画出来……
这些问题的提出,让学生在强烈的认知冲突中,形成思维的爆炸,比起让学生“画指定度数的角”、“量指定角的度数”这些封闭性问题更具挑战性,让这些与生活紧密联系的开放问题情境成为数学课堂承载思考的载体,并借助这个载体让学生感悟或掌握其中的思考元素,从而获得更有意义的思维发展,这样的课堂才会展现出数学教学最本真的价值。

