基于Thevenin的锂离子动力电池建模实验研究

， ，，

(1.广东海洋大学 电子与信息工程学院，广东 湛江 524088；2.河南工学院 电气工程系，河南 新乡 453003)

0 引言

锂电池荷电状态[1](state of charge，SOC)是动力电池组工作时的重要参数，可以为电池管理系统提供控制依据，其估计精度制约着系统优劣。但是SOC不能直接测量，由于电池本身是密闭的电化学反应，且电池组工作时电流变化剧烈，使得锂电池系统具有很强的非线性而难以精确建模。目前的锂离子电池模型[2]以纯数学模型、电化学机理模型、等效电路模型等为主，其中最常用的为等效电路模型。等效电路模型很好地描述了锂离子电池的电化学反应过程，其表达式简单，且等效电路模型非常容易转换为状态空间模型，可以应用于各种SOC估算算法，因此应用最为广泛。

锂电池充放电过程中电池内部发生着剧烈的电化学反应，温度、电流、使用次数等各种因素均会影响电池的各种指标。作为电池的重要参数，SOC有着多而复杂的影响因素，根据当今广泛认可的分类方法，可以分为可恢复性因素和不可恢复性因素两大类[3]。其中不可恢复因素对SOC造成的影响是不可逆的，这些因素和电池的制造工艺及是否使用恰当有关，不能通过后期保护修正，文中着重研究可恢复因素对SOC的影响，电解液密度的变化会导致锂电池开路电压(open circuit voltage,OCV)的规律性变化，且其最直观的表现就是电池内部的欧姆电阻和极性电阻值发生的变化；温度变化可以影响电池的化学反应，当温度在正常工作范围内升高时，可以使电池输出更多的能量，而锂电池工作温度过低，将停止释放能量。文中将实验用电池的工作温度稳定在20°左右，主要研究充放电电流对SOC的影响。

1 锂电池电特性分析

1.1 锂电池的开路电压特性

OCV是电池完全静置情况下正负极之间的电势差，OCV取决于电池的生产制造工艺，不受电池的尺寸、结构等因素影响。实验表明，当温度为恒定值时，锂离子电池的OCV与SOC有着直接对应的关系[4]。要分析锂电池的特性以及模型所需的各项参数就必须对电池进行充放电实验。表1给出了实验用锂电池的各项参数。实验用电池为磷酸铁锂，额定容量为10 Ah。

表1 电池参数表

在保障温度的前提下，设置脉冲放电电流为1 C(10 A)，以1 C电流对锂电池充电360 s，使SOC=40%增加至SOC=50%，静置一段时间后测量其OCV；再以1 C电流将锂电池充电360 s，使SOC=50%增加至SOC=60%，静置后测其SOC；循环充电、静置，直至将电池充至满电。根据静置时间的长短得到静置15分钟，静置30分钟，静置45分钟后的单体磷酸铁锂电池的SOC与OCV关系如图1所示。

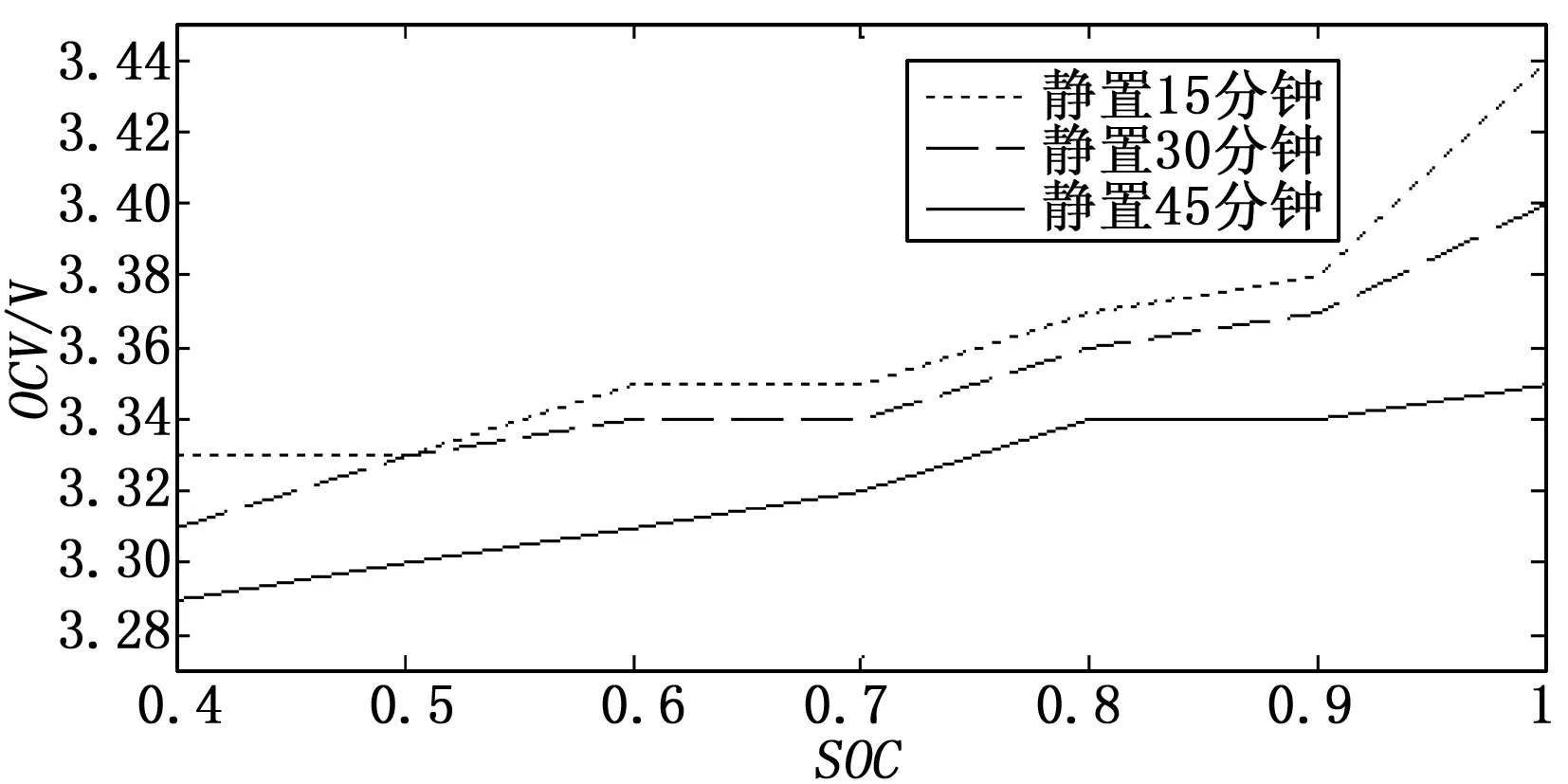
图1 电池SOC与OCV关系图

由图1可以看出，在单体电池充电过程中，SOC与OCV间确实存在着直接对应的关系。从这三条曲线可以看出，当静置时间延长，同一SOC下的OCV有所下降，这是因为随着静置时间的增加，锂离子电池内部的电化学反应逐渐平缓，使得OCV逐渐下降。实验证明，通常要静置一个小时左右才能测得准确的OCV，实验选取的静置时间为一个小时。

1.2 锂电池的内阻特性

电流通过电池时，在电池的正负两端会有一定的压降，这是由电池内阻产生的，锂离子电池的内阻是电池建模的一个重要指标，电池的内阻由欧姆内阻和极化内阻组成[5]，其中欧姆内阻受电池内部化学反应的影响较小，而极化内阻是由电池内部化学反应时产生的极化现象形成，内阻的表示如下：

R0=RΩ+Rp

(1)

其中:RΩ为欧姆内阻，Rp为极化内阻，RΩ和Rp的数值由系统参数辨识求得。

在保障温度的前提下，以1 C电流对实验用锂离子电池充电，每次充电10%，使其SOC从40%逐步充至100%。在充电停止的瞬间端电压变化类似阶跃响应原理，其中电压的瞬间下降由欧姆内阻产生；而其端电压变化产生曲线由电池的极化现象导致，记录电池端电压的恢复过程，利用一阶RC曲线可以辨识得到RΩ与Rp随SOC的变化如图2所示。

图2 RΩ与Rp随SOC变化曲线

从图2可以看出，在设置温度恒定的前提下，RΩ变化较小，而Rp变化剧烈，这是因为RΩ受电解液浓度影响，而电池工作过程中电解液浓度变化不大，仅是随着SOC的增加而略有增加。Rp也会随着SOC的增加有所增加，然而其受化学反应的极化程度影响更大，因此整个充放电过程中，Rp变化更为剧烈。论文探讨开路电压和内阻随SOC的变化情况，辨识得到实验电池的开路电压和内阻值，为后面建立电池的Thevenin模型打下基础。

2 锂电池模型的建立

戴维宁(Thevenin)模型[6]是最有代表性的等效电路模型，Thevenin模型的设计中将电池内部化学反应中的极化现象等效为极化电阻与极化电容，较好地实现了对电池动静态特性的模拟，其电路结构如图3所示。

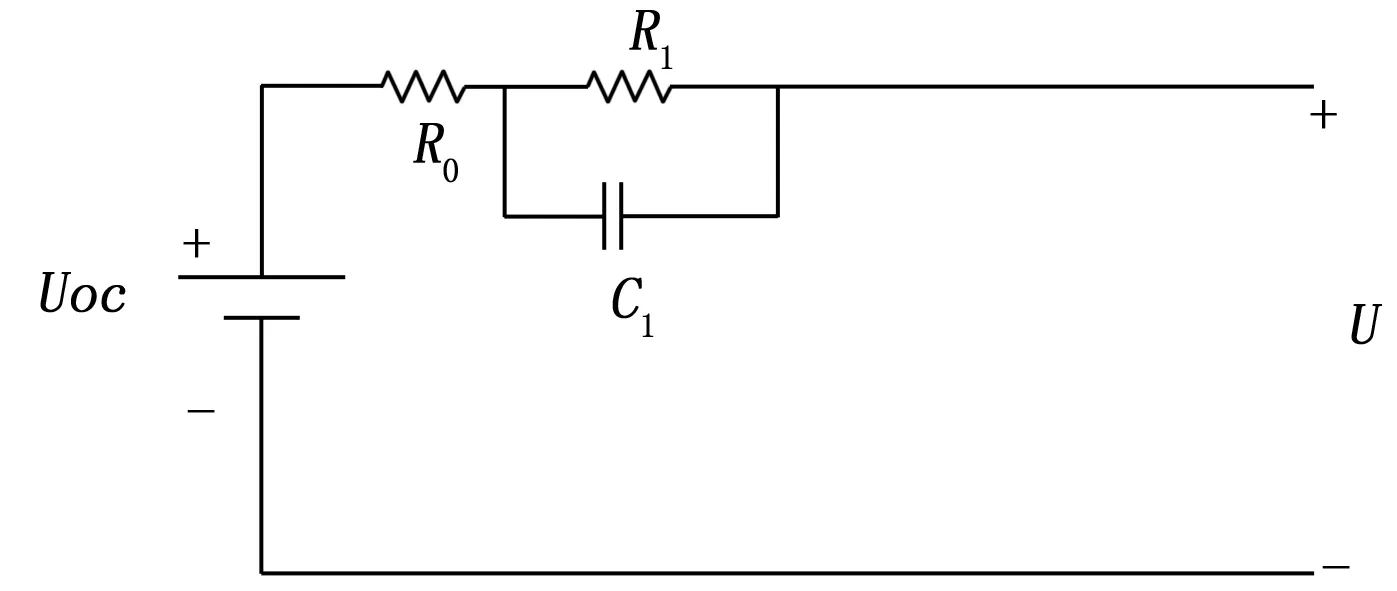
图3 戴维宁模型

在图3中，Uoc是电池的OCV，R0是其欧姆电阻，R1和C1分别是其极化电阻和极化电容，U是锂电池的端电压。

基于上面的Thevenin模型，建立实验用磷酸铁锂电池的状态空间模型，以锂电池的SOC和R1、C1并联电路的极化电压U1作为系统的状态变量，以电路中的电流ik为系统的输入，电路的工作电压(端电压)U为系统的输出，得到的离散状态空间模型的状态方程为：

(2)

得到的锂电池Thevenin模型的输出观测方程为：

(3)

式中，f(SOCk)表示的是由实验数据拟合得到的开路电压OCV与SOC的关系，其中实验数据由脉冲放电实验测得，f(SOCk)可以通过非线性最小二乘法拟合得到。

3 仿真实验的设计与分析

在建立Thevenin模型的状态空间的基础上，通过参数辨识进一步建立磷酸铁锂电池的Thevenin模型，以负载电压为系统输出，通过输出电压校验模型精度，并给出模型误差。

3.1 OCV与SOC关系的辨识

锂电池开路电压与荷电状态的关系辨识通过脉冲放电实验数据来实现，用1 C电流对电池进行放电，将电池的荷电状态由100%放电至10%，每次放电容量间隔为10%，同时每次放电结束后要使电池静置一个小时，以此时的电压为OCV，实验用电池为10 Ah磷酸铁锂电池。OCV与SOC之间为非线性关系，利用非线性最小二乘拟合方法可以得到其对应关系，以Matlab中的cftool为工具，拟合得到的曲线如图4所示。

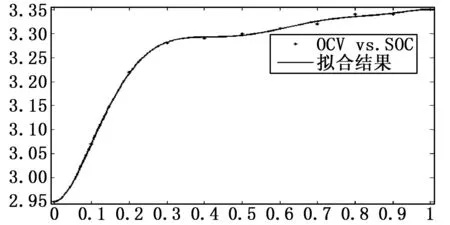
图4 OCV与SOC拟合结果

Matlab拟合结果如下：

Linear model Poly7:

f(x) = p1*x^7 + p2*x^6 + p3*x^5 + p4*x^4 + p5*x^3 + p6*x^2 + p7*x + p8

Coefficients (with 95% confidence bounds):

p1 = -51.94 (-125.3, 21.39)

p2 = 210 (-47.09, 467.2)

p3 = -339.9 (-696.4, 16.6)

p4 = 277.4 (29.76, 525.1)

p5 = -116.5 (-206.3, -26.66)

p6 = 21.21 (5.316, 37.11)

p7 = 0.01348 (-1.075, 1.102)

p8 = 2.95 (2.932, 2.968)

Goodness of fit:

SSE: 9.62e-005

R-square: 0.9994

Adjusted R-square: 0.998

RMSE: 0.005663

该拟合结果给出了拟合曲线的均方误差以及标准差，数据表明该拟合方法得到的SOC与OCV的曲线与实际曲线精确度较高。

3.2 RC参数辨识

电池模型中对应的电阻和电容参数值的辨识是通过混合脉冲功率 (hybird pulse power characterization,HPPC) 试验[7]来实现，辨识得到模型的欧姆电阻参数、极性电阻参数和极性电容参数。由于模型中的各个参数在不同SOC下的值变化不大，所以将Thevenin模型中的电路参数辨识为常数。利用一阶RC曲线辨识得到的Thevenin电路模型的参数值如表2所示。

表2 RC 参数表

表2中可以看出模型中各个参数在不同SOC下变化不大，所以后面模型中各参数值均选取的是锂电池SOC为50%时的实验数据。

数据拟合得到的对比结果如图5所示。

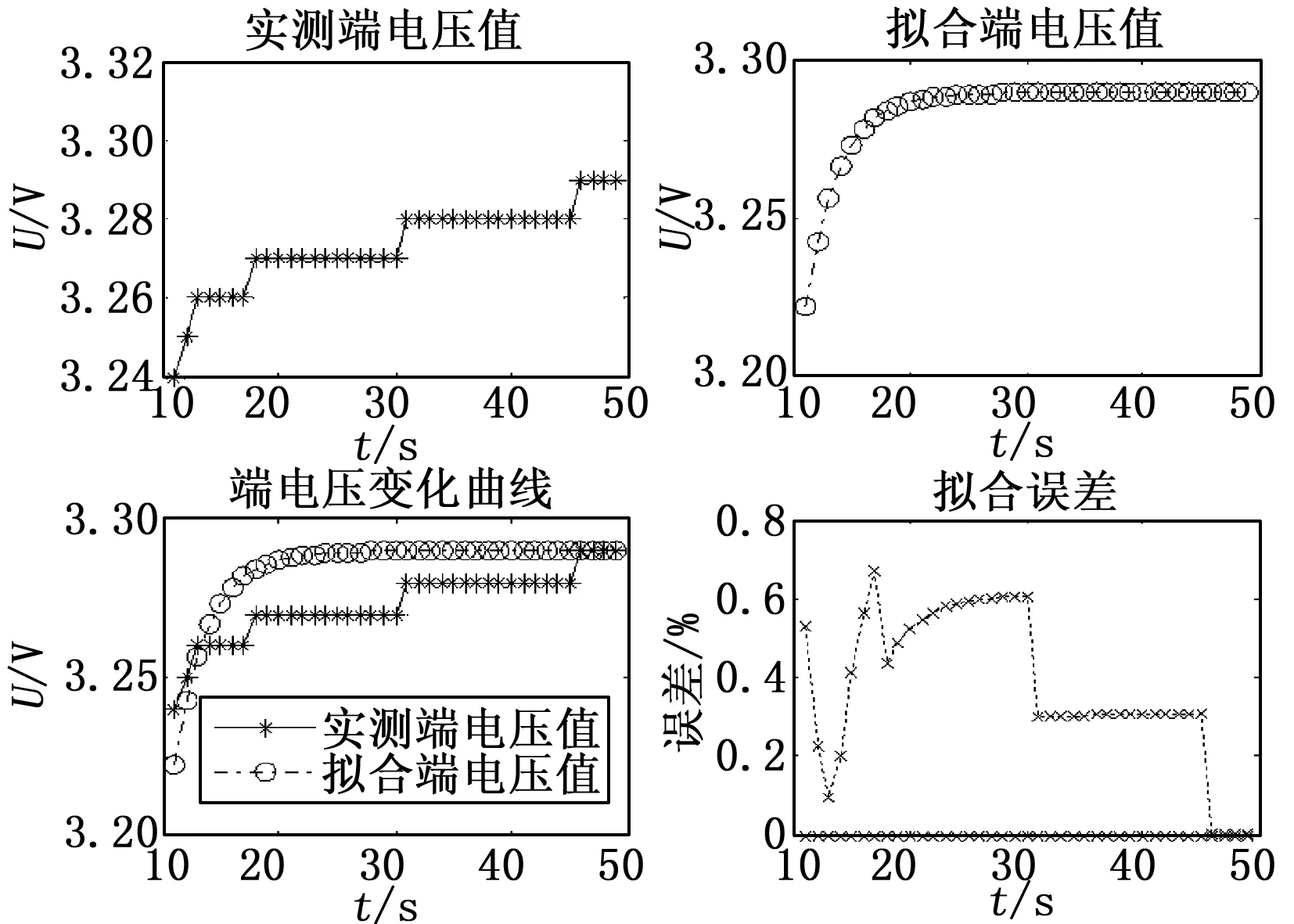
图5 RC参数辨识结果

图5中绘制了实测的端电压值，根据测量数据拟合得到的端电压值，以及将拟合端电压和实测端电压对比得到的拟合误差。可以看出，辨识得到的RC参数误差不大于0.7%，较好的跟随了端电压变化曲线，表2中RC参数值有效。

3.3 验证实验设计

通过参数辨识与数据拟合可以得到单体磷酸铁锂电池的Thevenin模型的各个参数，根据Thevenin模型的状态空间方程，在Matlab/Simulink中建立单体磷酸铁锂电池的结构如图6所示。

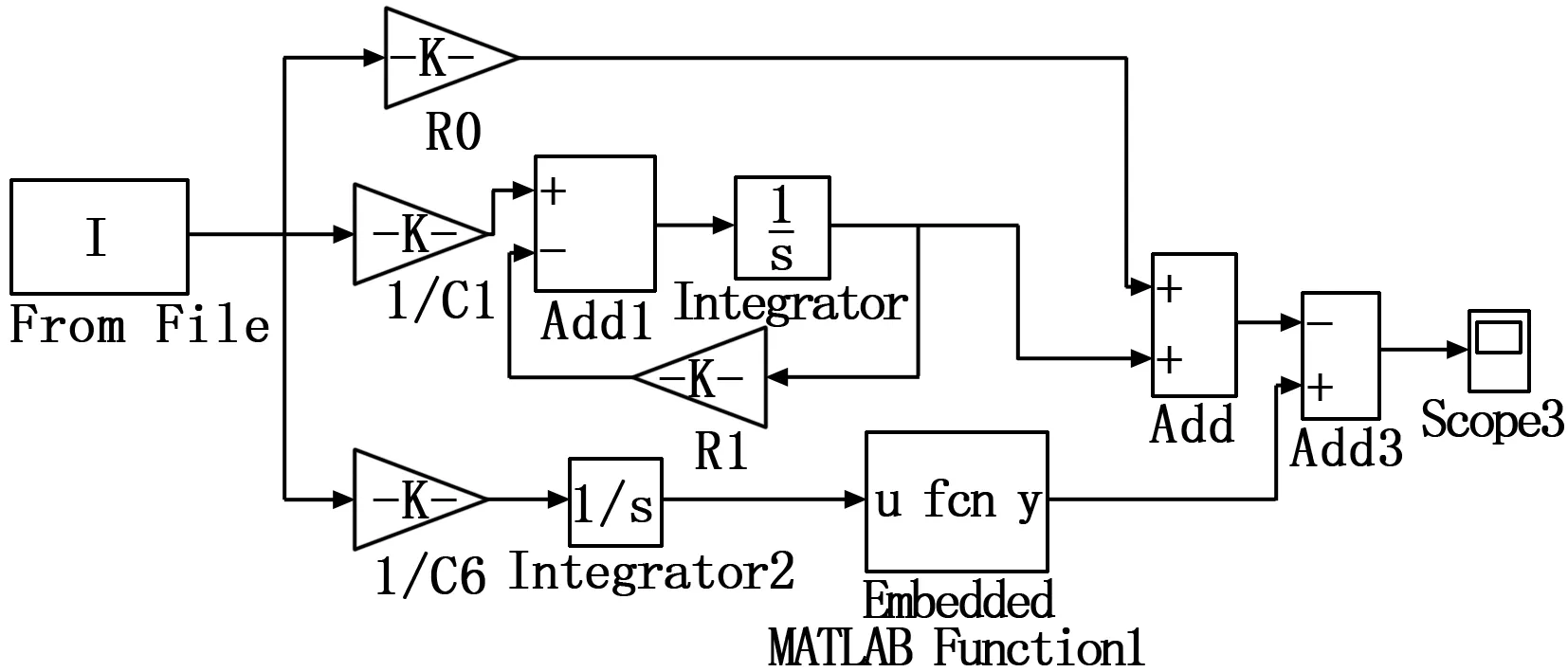
图6 Thevenin模型框图

图6中模型包含了实验用磷酸铁锂电池的状态空间模型。模拟电池工作过程，放电全程3 000 s，先以10 A的电流恒流放电，随后当电池SOC降低输出电流随着减小。将实验测得的放电电压、电流数据为输入量导入图6所示的状态空间模型，再将得到的模型输出与实验获得的端电压进行比较，得到的误差曲线如图7所示。

图7 误差曲线

通过图7对比分析可知，本文建立的磷酸铁锂单体电池的Thevenin模型，初期误差较大，最大值为0.1 V，随着放电的进行，误差逐渐降低，不超过0.04 V。初期误差大主要是由于Thevenin模型将状态空间模型参数辨识为常数，在放电初期不能很好跟随电压的变化，后期实验中可以增加变量以进一步提高模型精度。但总体来看，所建立的电池模型参数辨识合理，精度较高。

4 结束语

根据Thevenin动态电池等效模型，通过HPPC实验得到常温下的充放电数据，利用非线性最小二乘法对数据进行拟合和辨识，得到实验用磷酸铁锂电池模型。在Matlab/Simulink环境下建立了实验电池的仿真模型，设计了放电实验，实验证明所建立的电池模型参数辨识合理，误差不大于0.1 V，且不断收敛于真实值，精度较高。以该模型为基础，可以设计算法以实现锂电池SOC的实时监控。

参考文献：

[1] 刘胜永，李 源，赵振森，等.基于DSP的电动汽车锂电池荷电状态估算的研究与实现[J].计算机测量与控制，2015,23(10)：3533-3535.

[2] Yet H， Liu X T.A new model for State-of-Charge(SOC)estimation for high-power Li-ion batteries[J].Appl. Energy，2012,08：031-038.

[3] 张泽宇.基于决策树模糊等效电路模型的锂电池SOC估计方法 [D]：哈尔滨：哈尔滨工业大学，2016.

[4] 陈息坤，孙 冬.锂离子电池建模及其参数辨识方法研究 [J]：中国电机工程学报，2016，22(36)：6254-6261.

[5] 李振强，邹丽蓉，黄 杰.锂电池的模型参数与荷电状态估计的研究 [J].通信电源技术，2016,1：18-21.

[6] 张 阳，潘文霞.带可变参数锂离子电池 Thevenin模型[J].电源技术，2013,137(5)：755-757.

[7] 张 宾，郭连兑，李宏义,等.电动汽车用磷酸铁锂离子电池的PNGV 模型分析[J].电源技术，2009，33(5)：417-421.