带关节轴承的波纹管式功率分出轴模态计算方法
鞠振飞,雷 雷
(1.海军驻苏锡地区航空军事代表室;2.中国航发控制系统研究所,江苏无锡214063)
先进战斗机一般使用高速弹性联轴器将发动机附件齿轮箱的功率传递给飞机附件齿轮箱,见图1。这种联轴器还有一种名称叫功率分出轴[1-2],在高速运转(转速为10000~18000rpm)的同时,还需要补偿两端法兰之间由于安装或工作时产生的不对中[3]。
金属波纹管式功率分出轴是用2个波纹管组件直接与一根中介轴相连而成,是一种新型的联轴器。波纹管是一种外表面呈波纹状的薄壁件,一般用不锈钢或者钛合金加工制成,具有较高的轴向弹性和横向弹性[4-5]。此类联轴器的特点是重量轻、体积小、耐热性好、耐腐蚀性好,而且还具有变形吸收能力强的特性,因此广泛被应用于飞机附件传动轴系当中。
由于波纹管组件的刚度较弱,轴向承载能力差,一般是采用自润滑关节轴承来承受轴向力[6]。自润滑关节轴承主要由一个外球面内圈和一个内球面外圈组成,内外圈之间一般采用PTFE衬垫[7]。其结构简单紧凑、承载力大、滑动摩擦面是球面,内外圈之间可以做相对摆动,广泛被应用于航天航空、高速运输和军工装备等高精尖领域的机械设备中[8]。
在设计波纹管式功率分出轴时,其模态特性是需要重点关注的对象[9]。目前,主要关注的是关节轴承结构磨损寿命问题[10-14],而对于带关节轴承的功率分出轴动力特性研究几为空白。本文就带关节轴承的波纹管型功率分出轴模态分析方法进行讨论,以期能为国内相关单位设计波纹管式功率分出轴时提供具有工程指导意义的思路。
1 结构说明
本文将利用有限元方法对某型波纹管式功率分出轴进行模态分析。波纹管式功率分出轴属于轴对称结构。对于关节轴承而言,虽然一样属于轴对称结构,但在其外球面内圈和内球面外圈之间有一层厚度很薄(约0.5mm)的衬垫,见图2。

图2 关节轴承结构图Fig.2 Configuration of spherical plain bearing
关节轴承在波纹管式组件中的安装位置示意图见图3,外圈采用挡圈和轴承安装座固定,防止关节轴承在传递轴向载荷时被挤出。内圈通过螺帽与中间轴的轴颈锁紧。

图3 关节轴承与波纹管组件的分布结构Fig.3 Structure layout of spherical plain bearing and corrugated-pipe component
2 固有频率测试
为了分析有限元仿真计算方法的精确性,首先对功率分出轴进行模态试验。模态试验方法为脉冲锤击法,采用多点敲击单点测量的方式,激励力信号使用压电式力传感器进行采集,响应信号通过压电加速度计进行采集[15]。使用分析设备的主要功能是对脉冲信号和响应信号进行离散、采样,然后进行A/D转换,将模拟量信号变成有限位数的离散数字量。对这些数字量进行FFT变换,再进行功率谱、相干函数、传递函数等运算,最后根据传递函数值识别模态参数。
为分析关节轴承对波纹管型功率分出轴固有频率的影响,分别对带关节轴承的轴和不带关节轴承的轴进行锤击试验,试验测得的固有频率值见表1。试验过程中,采用夹具固定功率分出轴,见图4。经计算分析,该夹具可以模拟两端完全固支的状态。

表1 锤击法测固有频率试验结果Tab.1 Test solution of natural frequency measured by hammering method

图4 功率分出轴模态测试工装Fig.4 Modal test tooling of power take-off shaft
3 接触方法建模计算分析
基于ANSYS14.0平台,对波纹管型功率分出轴进行有限元建模。波纹管联轴器的主要部分采用SOLID185实体单元建模。关节轴承内外圈部分同样采用SOLID185单元建模,由于向心关节轴承不能约束横向变形,如果将其内外环直接粘合而视为一体结构进行建模处理是不恰当的。
直接按照静力学接触问题进行处理,由于润滑层的存在,直接假定成刚体-柔体接触,使用面-面接触单元形成接触对的方式,见图5。计算时,取实际安装边界条件,即两端完全固支。计算方法选用拉格朗日乘子法,不需要人为定义接触刚度去满足接触面间不可穿透的条件,可以直接实现穿透为零的真实接触条件。
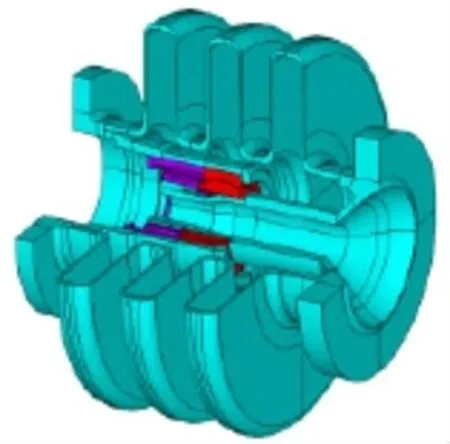
图5 关节轴承建模示意图Fig.5 Modeling diagram of spherical plain bearing
经过计算,得到前两阶横向固有频率分别为84Hz、111Hz,对应振型图见图6、7。可见,采用接触计算得到结果与不带关节轴承的功率分出轴计算结果较吻合。这是由于ANSYS软件进行模态计算时取的是初始接触刚度。
将接触状态设置为close gap,即无间隙接触,计算得到前两阶固有频率分别为326Hz、405Hz,对应振型见图8、9。计算结果与试验值仍然与较大误差。
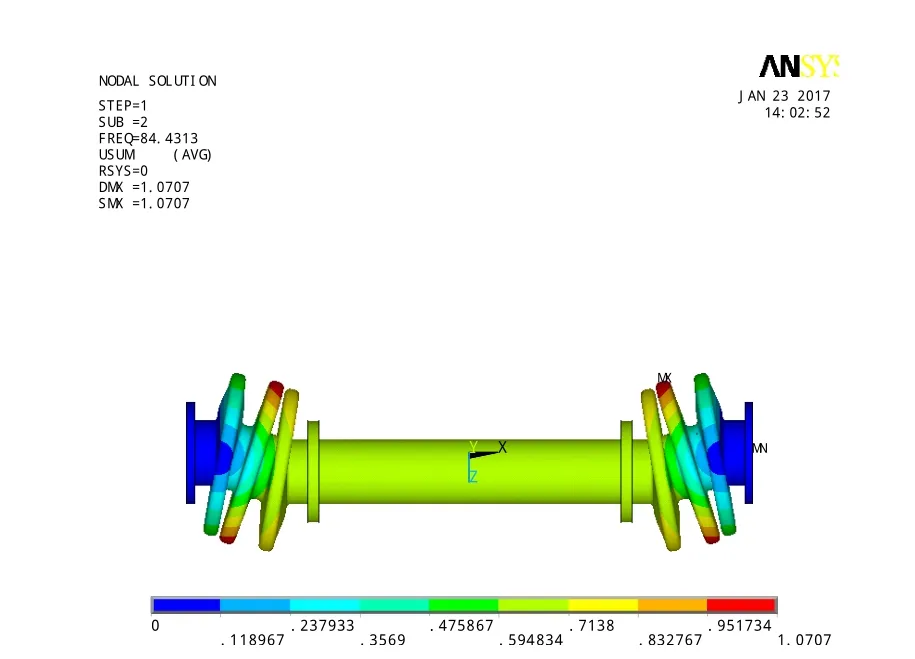
图6 一般接触条件的第一阶振型Fig.6 First modal in general contact conditions

图7 一般接触条件的第二阶振型Fig.7 Second modal in general contact conditions

图8 无接触间隙时第一阶振型Fig.8 First modal in close gap

图9 无接触间隙时第二阶振型Fig.9 Second modal in close gap
4 有限元模型改进
由计算结果可以发现,直接采用静力学接触问题进行计算,误差较大。而带关节轴承的波纹管型功率分出轴的模态分析属于非线性模态分析。非线性模态(NNMS)最初由美国加州大学伯克利分校的Rosenberg等人引入[16-17]。ANSYS由于具备较好的接触建模和线性模态分析的能力而被广泛采用,但因为非线性因素的控制难度较大,国外在碰到复杂非线性接触模态问题时采用的解决方法主要是自行开发不同的非线性模态分析求解器NLMA[18],这种方法工作量大,耗时长,不利于工程设计。
增加关节轴承后功率分出轴的固有频率有明显升高。说明增加关节轴承可直接提高系统的刚度。而采用静力学接触问题的方法进行计算时,ANSYS软件在计算时,忽略了关节轴承对功率分出轴系统刚度特性的影响。通过建立功率分出轴系统的刚度等效模型,见图10。关节轴承与波纹管组件属于并联系统,两端分别与中介轴相连,建模时不计系统阻尼。
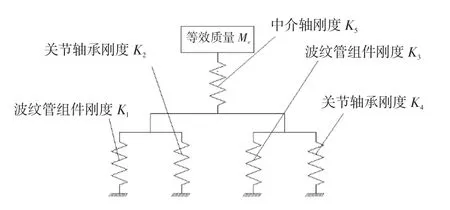
图10 功率分出轴系统的等效模型Fig.10 Equivalent theoretical model for flexural study
考虑两端组件和轴承的制造差异性,假设波纹管组件的等效刚度分别为K1、K3,关节轴承组件的等效刚度为K2、K4,中介轴的等效刚度为K5;系统总的等效质量为Me。
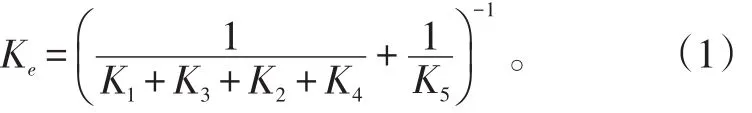
系统的固有频率则为:

结合ANSYS软件的特点,考虑在建模时在关节轴承内外环设定一个微小间隙(润滑层的厚度),关节轴承的刚度特性可通过建立弹簧单元的形式来模拟,如图11所示。

图11 弹簧单元模拟关节轴承等效刚度Fig.11 Equivalent stiffness of spherical plain bearing simulated by spring element
ANSYS中选用的的弹簧单元为COMBIN14单元,见图12。COMBIN14轴向的弹簧-阻尼器选项是一维的拉伸或压缩单元,其每个节点有3个自由度,即X、Y、Z轴向的移动,不能考虑弯曲和扭转,弹簧阻尼器没有质量,质量可通过质量单元另外来施加,弹簧和阻尼的特性可以直接在单元里赋予。
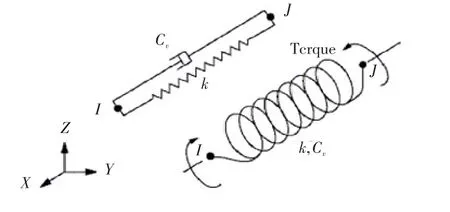
图12 COMBIN14单元示意图Fig.12 Diagram of combin14 element
在不带关节轴承的功率分出轴有限元模型上,在对应关节轴承处沿Y、Z方向各增加2个弹簧单元(夹角为90°),以模拟关节轴承的横向刚性。计算带关节轴承的波纹管型功率分出轴固有频率时的关键在于如何给定关节轴承刚度。假设两端关节轴承刚度相同,分别给定不同弹簧单元刚度时,有限元模型的前2阶固有频率计算结果见表2,拟合数据见图13。

表2 不同刚度下功率分出轴前两阶横向固有频率计算值Tab.2 Calculation of first and second lateral natural frequency of power take-off shaft in different stiffness
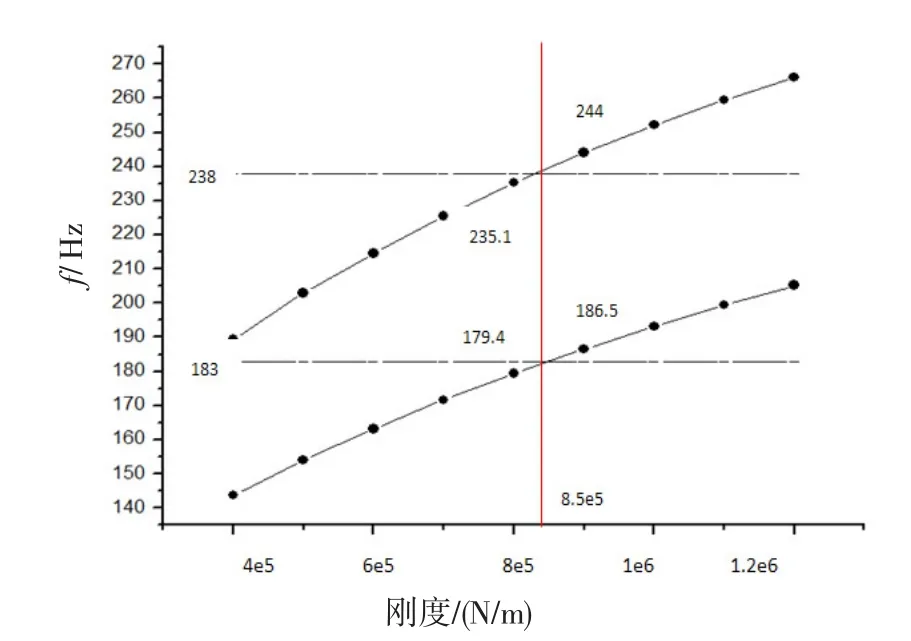
图13 刚度数据拟合图Fig.13 Fitting-figure of stiffness
功率分出轴的前2阶横向固有频率与关节轴承的等效刚度值基本呈线性关系。通过计算拟合,发现当取刚度为8.5×105N/m时,模型的前2阶固有频率值与试验比较接近,对应振型见图14、15。

图14 等效模型第一阶振型图Fig.14 First modal of equivalent model

图15 等效模型第二阶振型图Fig.15 Second modal of equivalent model
6 结论
在波纹管型功率分出轴使用环境下,关节轴承明显增强了波纹管组件的横向刚度。由于关节轴承呈明显的非线性特性,直接使用接触单元建模进行计算误差过大。
本文提出使用弹簧单元来模拟关节轴承的等效刚度方法来计算波纹管型功率分出轴的模态特性,发现关节轴承的等效刚度与功率分出轴的固有频率呈基本线性关系,当取关节轴承刚度为8.5×105N/m时,有限元计算结果与试验结果非常接近,说明使用该方法来计算波纹管联轴器的固有频率比较合适。
参考文献:
[1]衡井武,陆际午.膜盘式功率分出轴(PTO)的研究[C]//第十届航空发动机动力传输学术讨论会.大同:中国航空学会,2001:202-208.HENG JINGWU,LU JIWU.Research on the diaphragm power take-off(PTO)shaft[C]//Proceedings of the 10thCSAA(engine)small engine.Datong:CSAA,2000:164-167.(in Chinese)
[2]NAGESH S,JUNAID BASHAA M,THAKUR DINESH SINGH.Dynamic performance analysis of high speed flexible coupling of gas turbine engine transmission system[J].Journal of Mechanical Science and Technology,2015,29(1):173-179.
[3]赵蕴斌,薛志宏,王昭甫.挠性联轴器性能分析[J].热能动力工程,2002,17(3):308-309.ZHAO YUNBIN,XUE ZHIHONG,WANG ZHAOFU.An analysis of the performance of a flexible coupling[J].Journal of Engineering for Thermal Energy&Power,2002,17(3):308-309.(in Chinese)
[4]于向阳.波纹管联轴器的有限元仿真分析[J].福建电脑,2014(11):10-12.YU XIANGYANG.Finite element method analysis of corrugated-pipe coupling[J].Fujian Computer,2014(11):10-12.(in Chinese)
[5]赵连生,王平,王心丰.新型波纹管联轴器的非线性有限元分析[J].南京航空航天大学学报,1997,29(4):412-417.ZHAO LIANSHENG,WANG PING,WANG XINFENG.Nonlinear finite element method analysis of a new type bellows coupling[J].Journal of Nanjing University of Aeronautics&Astronautics,1997,29(4):412-417.(in Chinese)
[6]DAVID F VORACEK.Monitoring techniques for the x-29 aircraft’s high-speed rotating power takeoff shaft:NASA technical memorandum:101731[R].Los Angeles:NASA,1990:1-25.
[7]曲庆文,刘源勇.关节轴承的设计特点及分析[J].润滑与密封,2004,29(4):102-105.QU QINGWEN,LIU YUANYONG.Design characteristic and analysis for the spherical plain bearing[J].Lubrication Engineering,2004,29(4):102-105.(in Chinese)
[8]韩苏征,胡忠会.飞机机体用金属对金属关节轴承[J].轴承,2016(8):61-65.HAN SUZHENG,HU ZHONGHUI.Metal to metal spherical plain bearings for airframe[J].Bearing,2016(8):61-65.(in Chinese)
[9]TADEO A T,CAVALEA K L.A Comparison of flexible coupling models for updating in rotating machinery response[J].Journal of Brazilian Society of Mechanical Science and Engineering,2003,25(3):235-244.
[10]苏高峰,薄玉成.杆端向心关节轴承动应力下疲劳寿命分析研究[J].机械设计,2013,30(3):89-92.SU GAOFENG,BO YUCHENG.Fatigue life analysis and research on rod end spherical plain bearings under dynamic stress[J].Journal of Machine Design,2013,30(3):89-92.(in Chinese)
[11]胡占齐,李巍,杨育林,等.航空关节轴承寿命试验机发展综述[J].轴承,2015(11):57-63.HU ZHANQI,LI WEI,YANG YULIN,et al.Review on development of life testers for aircraft spherical plain bearings[J].Bearing,2015(11):57-63.(in Chinese)
[12]柏耀星,邱明,李迎春,等.关节轴承磨损失效的研究现状及进展[J].现代制造工程,2012(4):138-142.BO YAOXING,QU MING,LI YINGCHUN,et al.Study status and development of the wear failure of spherical plain bearing[J].Modern Manufacturing Engineering,2012(4):138-142.(in Chinese)
[13]李巍,胡占齐,杨育林.航空自润滑关节轴承寿命试验机的构型[J].中国机械工程,2016,27(6):742-747.LI WEI,HU ZHANQI,YANG YULIN.Configuration of aerial self-lubricating spherical plain bearing testers[J].China Mechanical Engineering,2016,27(6):742-747.(in Chinese)
[14]卢建军,邱明,李迎春.自润滑向心关节轴承磨损寿命模型[J].机械工程学报,2015,51(11):56-63.LU JIANJUN,QU MING,LI YINGCHUN.Wear life models for self-lubricating radial spherical plain bearing[J].Journal of Mechanical Engineering,2015,51(11):56-63.(in Chinese)
[15]曹树谦,张文德,萧龙翔.振动结构模态分析:理论、实验与应用[M].天津:天津大学出版社,2001:50-73.CAO SHUQIN,ZHANG WENDE,XIAO LONGXIANG.Modal analysis of vibration structure:theory experiment and application[M].Tianjin:Tianjin University Press,2001:50-73.(in Chinese)
[16]ROSENBERG R M,ATKINSON C P.On the natural modes and their stability in nonlinear two degrees of freedom systems[J].Journal of Applied Mechanics,1959,26:377-385.
[17]陈予恕,吴志强.非线性模态理论的研究进展[J].力学进展,1997,27(3):289-300.CHEN YUSHU,WU ZHIQIANG.Advances in study on theories of nonlinear normal modes[J].Advances in Mechanics,1997,27(3):289-300.
[18]MAZZILLI C E N,BARACHO NETO.Evaluation of non-linear normal modes for finite-element modes[J].Computers and Structures,2002,80(11):957-965.

