混凝土等准脆性材料的应变软化模型研究

沈欣欣

（安徽理工大学 土木建筑学院，安徽 淮南 232001）

应变软化是混凝土的重要力学行为之一，即混凝土受载超过其强度后，材料的承载力随着变形的增加而逐渐降低的现象。传统的应变软化模型在数值计算时引起不适定性边界值问题和单元网格尺寸依赖性问题。网格尺寸相关性主要体现在：随着有限单元离散化精细化的增加，能量耗散趋近于零，这一现象显然违背了物理能量守恒定律。因此，消除网格相关性是混凝土应变软化模型应用于结构数值分析亟需解决的问题。

在连续介质力学的框架内，可以通过正则化方法避免网格尺寸相关性问题，如：积分类型的局部模型、梯度类型的局部模型、黏性模型、微极平面模型、内聚区模型。本文重点介绍前四个方法。

1 积分类型的局部模型

积分类型的非局部方法是对某一个点的空间领域上的加权平均来获得非局部对应变量。如果f（x）是区域V的局部场，特征区域内的相关非局部场[1]可以定义为：

式（1）中：α（x，ξ）为非局部加权函数。

在软化材料应用中，要求非局部算子不能改变场的一致性，要求加权函数必须满足归一化条件。

在无限的、各向同性的均匀的介质中，加权函数只取决于源点ξ和接受点x之间的距离r=‖x－ξ‖。因此，当α∞（r）反映非局部影响的加权函数，且单调递减时，α∞（r）可以表示为α（x，ξ）=‖x－ξ‖。非局部相互半径R指x与ξ之间的微小距离。域x的影响区域是以x为中心，半径R的实体。

在有限区域边界附近，假定均值是依赖实体域影响的一部分。为了满足式（2），加权函数通常定义为：

2 梯度类型的局部模型

梯度模型通常由包含高阶空间导数的差分方程来描述。梯度模型一般基于塑性形式、损伤形式或者两者的结合形式建立。由于模型需要高阶空间微分导数，因此，模型也需要更多的单元离散网格。隐式梯度关系可通过被积函数表示：

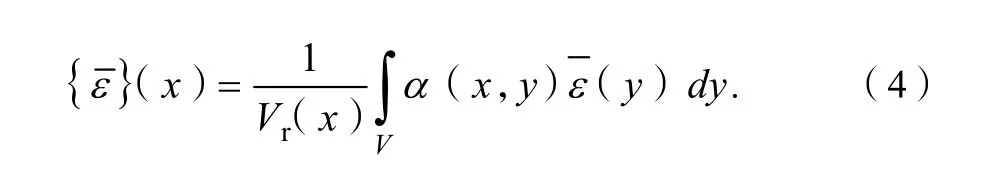
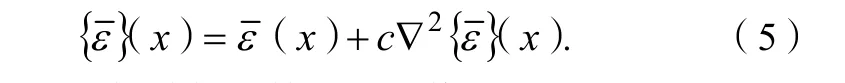
式（5）中：▽2为拉普拉斯算子，正值标量c决定非局部影响的宽度和长度。

为了求解式（5），通常体表面∂V上的边界条件是：

3 黏性模型

基于Duvaut-Lions模型，使混凝土具有黏性效应，利用该效应正则化，建立黏性正则化的率无关塑性损伤模型。非弹性应变率可以定义为：

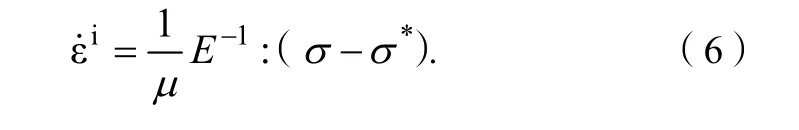
式（6）中：σ*为应力σ在屈服面上的投影；μ为黏性参数，即黏塑性系统的松弛时间。

4 微平面模型

微平面模型假定微平面的应变是宏观应变张量的解析分量。微平面是法向应变和剪切应变作用的结果，而且应变方向与剪应力张量方向一致。每个微平面上的响应取决于横向应变，只要微平面卸载，其应力-应变曲线路径就是独立的，卸载和再加载期间，应力-应变曲线路径不同于卸载，且是独立的；每个微平面上体积响应、偏响应、剪响应都是相互独立的。

为了应用方便简化参数，以微平面模型二为例，微平面主要表征微观结构框架内弱平面的行为。每个微平面上应力和应变分量较少，且不满足张量不变性。在所有空间方向上对其积分，实现满足宏观层面上的张量性要求。微平面模型二的控制方程如下：

式（1）中：CV，CD，CT为割线模量；σC为宏观应力不变量，通常称为约束应力，其值为中主应力和最小主应力的均值。

该模型能够很好地描述混凝土非线性三轴行为，能够真实地刻画扩张和摩擦、在静水压力增加时的脆性延性转变、不同程度的路径相关性、静水压试验中的硬化响应、拉伸和压缩时的应变软化等其他特征。

5 结论

非局部模型需要较多的有限元网格来离散结构，这使得该类模型不适合于大规模结构计算；从物理角度看，在本构关系中引入粘性正则化方法不符合混凝土在短期静态荷载作用下的准脆性材料本质；微极平面模型需要较多的模型参数并且参数难以确定。

参考文献：

［1］张浠，王勇，陈振富.混凝土的非局部损伤模型［J］.福州大学学报，1996（S1）：78-83.

［2］罗冬梅，李光霞.以塑性应变和损伤为参变量的广义非局部损伤本构方程［J］.内蒙古工业大学学报，1997（03）：89-94.

［3］Peerlings R H J，De Borst R，Brekelmans W A M，et al.Gradient enhanced damage for quasi-brittle material.International Journal for Numerical Methods in Engineering，2015，39（19）：3391-3403.

［4］Peerlings R H J，Deborst R，Brekelmans W A M，et al.Localisation issues in local and nonlocal continuum approaches to fracture.European Journal of Mechanics-A/Solids，2002，21（02）：175-189.

［5］杨璐，朱浮声，沈新普.梯度依赖的混凝土弹塑性非局部损伤的本构模型［J］.材料研究学报，2007，21（05）：477-481.

［6］Geers，M.G.D.Experimental analysis and computational modelling of damage and fracture.Holland： Technical University of Eindhoven，Eindhoven，1997.

［7］Lee J，Fenves G L.A plastic-damage concrete model for earthquake analysis of dam.Earthquake Engineering and Structural Dynamics，1998，27：937-956.

［8］Duvaut G，Lions J L.Inequalities in Mechanics and Physics（translated from the French by C.W.John）.New York：Springer，1976.

［9］Bažant Z P，Prat P C.Microplane model for brittle plastic material：Ⅰ.Theory.Journal of Engineering Mechanics，1988（114）：1672-1688.

［10］李树山，高丹盈，贾明晓，等.钢纤维混凝土微平面本构模型［J］.水利学报，2012，43（12）：1457-1463.