一种支持权重的改进K-means聚类算法

方振东，汪峰坤

聚类是数据挖掘技术中重要的应用方法，它利用所定义的“距离”概念把数据集分成多个类或簇［1］，使得同一簇中的数据对象相似度较高，不同簇中的数据对象相似度较低。聚类算法一般分成四类，分别是层次聚类算法、划分聚类算法、密度聚类算法以及其他聚类算法，其中K-means聚类算法［2］是一种提出较早、应用较广泛的聚类算法，其他聚类算法都是基于K-means聚类算法进行改进的。K-means算法的优点包括实现简单、收敛速度快、能有效地处理大数据集等。经典K-means算法的缺点有聚类结果容易只得到局部最优解、孤立点对聚类结果影响较大、聚类结果受初始数据对象影响较大、只能对凸形数据进行聚类、算法要求提前给出类的个数及不支持权重等［1-3］。

已有研究人员针对K-means算法存在的缺陷提出了改进办法。如：针对K值要提前给出的问题，刘晓悦等［4］提出了两段法，先使用 Canopy算法处理数据集，计算出K值和初始的类中心位置，再进行K-means算法详细聚类。郑富兰等［5］提出了每个聚类簇中由一个点作为簇代表，提高了聚类的效率。针对K-means算法无法对任意形状的数据集有效聚类的问题，邢长征等［6］提出了以平均密度作为聚类中心的改进算法。公茂果等［7］提出了流形距离，使算法能适用于复杂分布的数据聚类问题。

在聚类的现实应用中，各维的重要性都不同。例如，在职工健康体检的生化检查包含的子项中，白蛋白/球蛋白、低密度脂蛋白（LDL）、空腹血糖（GLU）和高密度脂蛋白（HDL_C）等健康指标的重要性是有区别的。重要性一般由专家给出的权重表示，但在经典的K-means算法中是不支持维的权重值的。

我们提出了支持权重的K-means改进算法并通过仿真实验验证所提出改进算法的有效性。

1 改进算法

1.1 算法的基本数据结构

设待聚类的数据集D中数据对象个数为n，每一个数据对象都由M维数据组成，不同的数据具有不同的权重，数据对象的值记为V1，V2，…，Vn。 每维数据的权重为 R1，R2，…，Rn，给定聚类数为 K 个。

改进算法使用到的数据结构如下：

权重Hash表R中每个键值对表示数据对象中的一个维，键取值为维（即属性）名称，值为相应属性的权重。在支持权重的聚类应用中，数据对象维数一般不是很高，使用Hash表可以快速得到维相应的权重。

每一个数据对象都使用浮点类型数组表示，数组下标对应相应的维，数组值为数据对象相应维的值。

簇用自定义类表示，类中有数据对象列表和簇中心点坐标对象。数据对象列表中是该簇中所有的数据对象，中心点坐标对象表示该簇计算得到的中心点坐标。

1.2 算法流程及计算公式

算法流程如下：

1）随机选择K个数据对象作为初始簇的中心点。

2）循环遍历其余数据对象，计算数据对象到K个簇中心点的距离。

3）将数据对象加入到距离最近的簇中。

4）重新计算加入新数据对象后簇的中心点坐标。

5）直到所有数据对象加入完成。

6）转到2），直到未出现数据对象被重新分配到其他簇的情况。

K-means算法常用的计算簇内距离公式是欧几里德公式

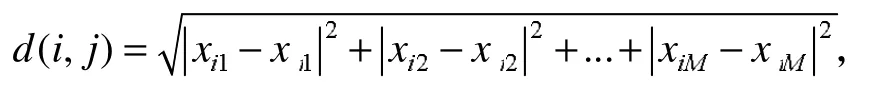
其中 i=xi1，xi2，…，xiM和 j=xj1，xj2，…，xjM是两个 M 维的数据对象。

经典的K-means算法无法体现各维的重要性，而本算法对簇内距离的计算公式进行了改进，使改进后的K-means算法支持权重。改进后的距离计算公式为

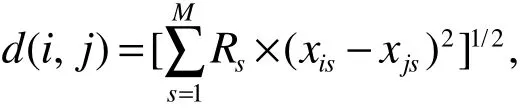
其中Rs表示第s维数据的权重，且Rs＞0。

改进后计算公式仍然满足距离要求，即距离是非负的、数据对象与自身的距离为0、距离是对称的、距离满足三角不等式。

K-means算法针对簇中心点的计算方法常用的是均值法，即簇中任意维坐标中心点为改进后的计算公式为，Rs为相应维的权重。

对于在迭代过程中计算簇中心点，K-means使用的方法是遍历簇中所有数据对象，通过公式进行计算，时间复杂度为O（n）。本算法改为直接利用上一次计算出的中心点，可将算法的时间复杂度减少为O（1）。具体思路是：设上一次计算某维中心点坐标为 x ’，簇中数据对象个数为m个，加入数据对象的相应维坐标为x，则加入数据对象后相应维坐标计算公式为x = ( x’× m + x ) /(k +1)。

综上，相对于经典的K-means算法，我们主要进行了两方面的改进：1）修改了簇的中心点和簇内距离的计算公式，使算法支持维权重；2）对迭代过程中的中心点计算公式进行了修改，使算法的时间复杂度降低。

2 改进算法实验与分析

2.1 算法流程实验

设某数据集中有8条数据，每条数据固定有3个属性，这3个属性的权重分别是8、4和1，聚类个数K取值为3。数据见表1。

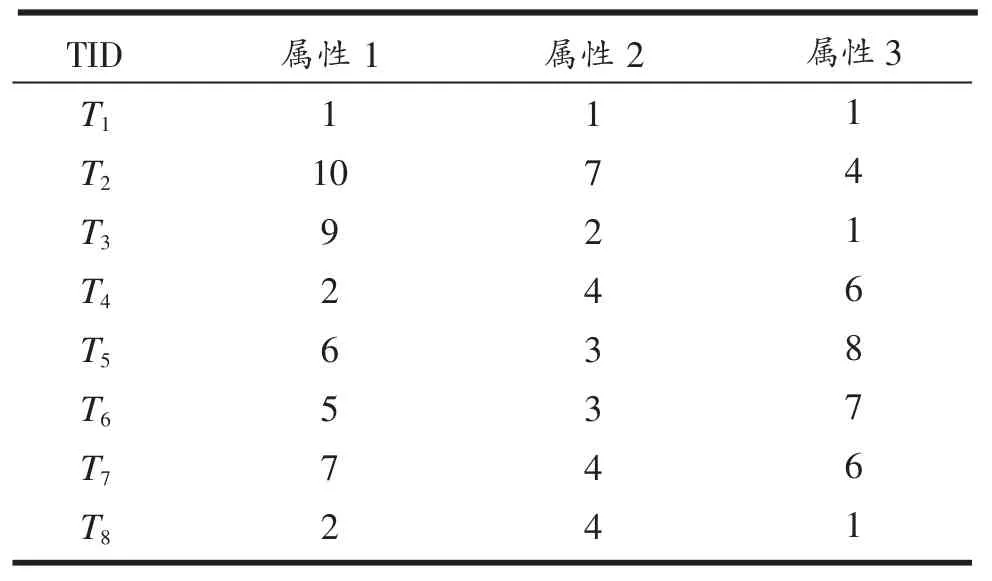
表1 聚类数据示例

经典的K-means算法不支持维的权重。在不考虑维权重的情况下，聚类过程如下：

1）为了简单，我们按顺序选择初始簇。前（K-1）个簇中每个簇的元素个数为，其余元素放到第K个簇。簇 1数据对象为 {T1，T2}，中心点坐标为（5.5，4，2.5）；簇 2 数据对象为{T3，T4}，中心点坐标为（5.5，3，3.5）；则簇 3 数据对象为{T5，T6，T7，T8}，中心点坐标为（5.5，3，5.5）。

2）第一次迭代后，簇 1 数据对象为{T2，T3，T4}，中心点坐标为（7，4.3，2）；簇 2 数据对象为{T1}，中心点坐标为（1，1，1）；簇 3 数据对象为{T5，T6，T7，T8}，中心点坐标为（5.3，5，5.5）。

3）第二次迭代后，簇 1 数据对象为{T2，T3}，中心点坐标为（9.5，4.5，2.5）；簇 2 数据对象为{T1，T4}，中心点坐标为（1.5，2，5.1）；簇 3 数据对象为{T5，T6，T7，T8}，中心点坐标为（5.3，5.5，5.5）。

4）第三次迭代，无交换数据，结束。

本算法支持维的权重，聚类过程如下：

1）初始簇仍然使用顺序选择。簇1数据对象为{T1，T2}，中心点坐标（5.5，4.2，2.5）；簇 2 数据对象为{T3，T4}，中心点坐标为（5.5，3，3.5）；簇 3 数据对象为{T5，T6，T7，T8}，中心点坐标为（5，3.5，5.5）。

2）第一次迭代后，簇1数据对象为{T2}，中心点坐标为（10，7，4）；簇 2 数据对象为{T3，T7}，中心点坐标为（8，3，3.5）；簇 3 数据对象为{T1，T4，T5，T6，T8}，中心点坐标为（3.2，3，4.6）。

3）第二次迭代后，簇1数据对象为{T2}，中心点坐标为（10，7，4）；簇 2 数据对象为{T3，T5，T7}，中心点坐标为（7.3，3，3.5）；簇 3 数据对象为{T1，T4，T6，T8}，中心点坐标为（2.5，3，3.75）。

4）第三次迭代后，簇1数据对象为{T2}，中心点坐标（10，7，4）。 簇 2 数据对象为{T3，T5，T6，T7}，中心点坐标（6.75，3，3.5）；簇 3 数据对象为{T1，T4，T8}，中心点坐标为（1.6，3，2.6）。

5）第四次迭代，无交换数据，结束。

可以看出，引入权重后，簇类结果发生了变化，且权重越大的维在计算距离时产生的作用越大。

2.2 算法性能比较

测试数据选择某医院职工健康体检中数据，共有10维，K=2，数据量从1万条增加到20万条。

由图1中可见，当数据量较小时，两种算法性能相近，但在数据量较大时，本文算法要略优于K-means算法。

图2是数据为10维，数据量为5万条，在不同K值时算法性能的比较。由图2可见，两种算法运算时间与K值相关，随着K值的变化运算时间发生变化。总体上，改进算法相对于K-means算法在运行时间上略有减少。

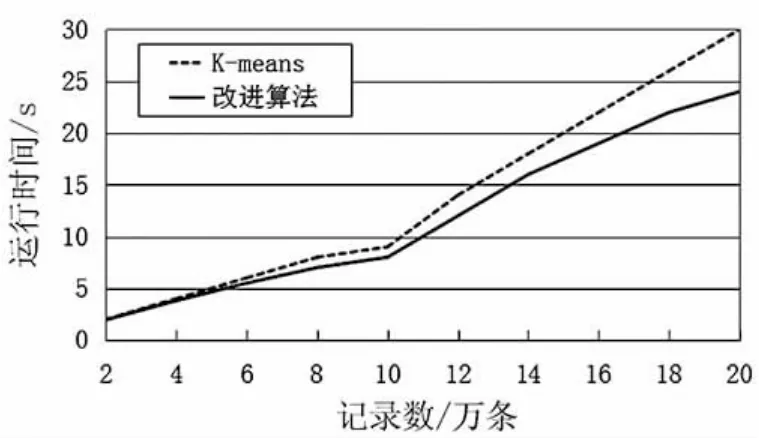
图1 不同数据量时算法性能比较

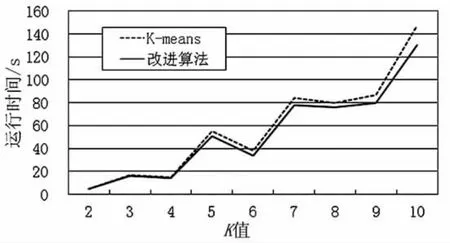
图2 不同K值时算法性能比较

3 结束语

我们根据实际聚类应用的需求，提出了支持不同维权重的改进的K-means算法，改进了簇中心点计算公式和簇内距离计算公式，使公式支持维的权重。我们对在算法迭代过程中的中心点计算流程进行了优化，使改进算法的性能有了一定的提高。

参考文献：

［1］ JAIN A K,MURTY M N,FLYNN P J.Data clustering:a review［J］.ACMcomputing surveys,1999,31（3）:264-323.

［2］ HARTIGAN J A,WONG M A.A K-means clustering algorithm［J］.Applied statistics,1979,28（1）:100-108.

［3］ MAULIK U,BANDYOPADHYAY S.Genetic algorithmbased clustering technique［J］.Pattern recognition,2000,33（9）:1455-1465.

［4］ 刘晓悦，郭强.海量用电数据并行聚类分析［J］.辽宁工程技术大学学报（自然科学版），2016，35（1）：76-80.

［5］ 郑富兰，张艳芳，吴瑞.基于 leader的 K-means改进算法［J］.山西师范大学学报（自然科学版），2014，28（4）：26-29.

［6］ 邢长征，谷浩.基于平均密度优化初始聚类中心的K-means算法［J］.计算机工程与应用，2014，50（20）：135-138.

［7］ 公茂果，王爽，马萌，等.复杂分布数据的二阶段聚类算法［J］.软件学报，2011，22（11）：2760-2772.