精心选用生活现实，积极践行“学材再建构”——以平方根（第1课时）教学为例

☉江苏省苏州市工业园区第十中学 李雪琼

著名特级教师李庾南老师及其团队近年来提出“三学”（学材再建构、学法三结合、学程重生成），这是针对课例研究的一种操作要义，值得深入研习和积极实践.笔者近期有机会执教平方根（第1课时）研讨课，积极践行李老师的“学材再建构”理念，对平方根的第1课时的教材内容进行了再建构，取得了较好的教学效果.本文记录该课的教学流程，并跟进教学思考，提供研讨.

一、平方根（第1课时）教学流程

教学环节（一） 创设情境，引入新课

生活问题1：学校要举行美术作品比赛，小红裁了一块边长为7dm的正方形画布，准备画上自己的作品参加比赛，那么这块正方形画布的面积是多少？

生活问题2：小欧也准备参加比赛，他想裁出一块面积为25dm的正方形画布，那么这块正方形画布的边长应取多少？

预设问题：这两个问题有什么不同？放到式子中看，它们是已知什么求什么？（板书：已知底数求它的二次幂；已知二次幂求它的底数）已知底数求它的二次幂，也就是平方你学过了吗？会求吗？已知二次幂求它的底数你学过了吗？今天我们就来研究这些问题.

设计意图：学生在七年级上册已学习了有理数，并且学习了有理数的加、减、乘、除、乘方运算.随着对数的认识不断深入，人们发现，生活中存在的数并不全部都是有理数，比如面积为2的正方形的边长就不是.数系扩充到实数就十分必要，通过两个生活情境问题引入数的开方，可以让学生感受一类新数产生的自然而然.

教学环节（二） 特例引路，定义开方

问题1：将“52=25”中的底数5擦除，改为括号，可以填什么数？

预设：学生填数，得到根据平方运算，可以填±5.

问题2：已知指数2及幂，求底数：

（ ）2=1；（ ）2=9；（ ）2=16；（ ）2=36；（ ）2=0.25.

定义开方：在乘方中，25是±5的平方，也叫二次方，反过来，我们把±5叫做25的平方根，已知指数、幂逆过来求底数的过程，称数的开方.这些定义内容及时板书.

教学组织：在定义一种新的运算之后，安排学生结合下面的表格说出谁是谁的平方根，加深对概念的理解.

x2 1 9 16 25 36 x ±1 ±3 ±4 ±5 ±6

在学生初步理解平方根定义后，进一步给出算术平方根的概念，并指出数的平方与开平方互为逆运算.并介绍目前已学到的6种运算分别是三对互逆运算（加与减、乘与除、乘方与开方）.

教学环节（三） 例题训练，巩固新知

例1 判断以下说法是否正确：

（2）6是36的一个平方根；

（3）-5是25的算术平方根；

（4）0.01是0.1的算术平方根.

设计意图：通过这组例题的训练，让学生加深对新概念的理解．可以安排学生先讲，其他学生参与评析、辨析．如果有不恰当的表述时，抓住这些错误资源，融入新课进程，引导学生回到定义来判断．

例2 求下列各数的平方根与算术平方根：

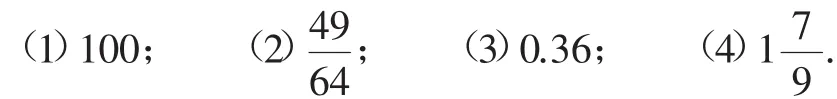
教学组织：师生共同完成第（1）题后，后面3个小题由学生上台板演.然后组织学生观察各式平方根的共同点，得出结论：有两个平方根且互为相反数.

预设追问：是不是所有数的平方根都是两个且互为相反数？（学生讨论后全班交流，归纳并板书性质）

教学环节（四） 定义符号，平方根与算术平方根的表示

分组活动：同学们现在能求一个数的平方根了吗？小组内一个同学说出一个数，然后让其他同学求它的平方根.

教学组织：由学生说的非平方数顺势给出平方根和算术平方根的表示并板书.

结合前面的例题，让学生学习书写平方根的符号，解决学生提出的非平方数的平方根.

例3 直接写出下列各式的值：

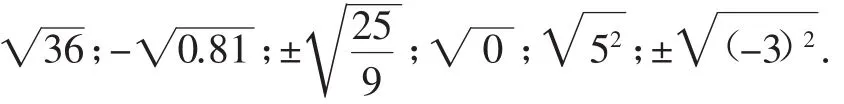
教学组织：学生口答并说出各式的含义，并要求学生观察式子的符号与结果符号的关系.

教学环节（五） 小结与作业（略）

附：板书设计

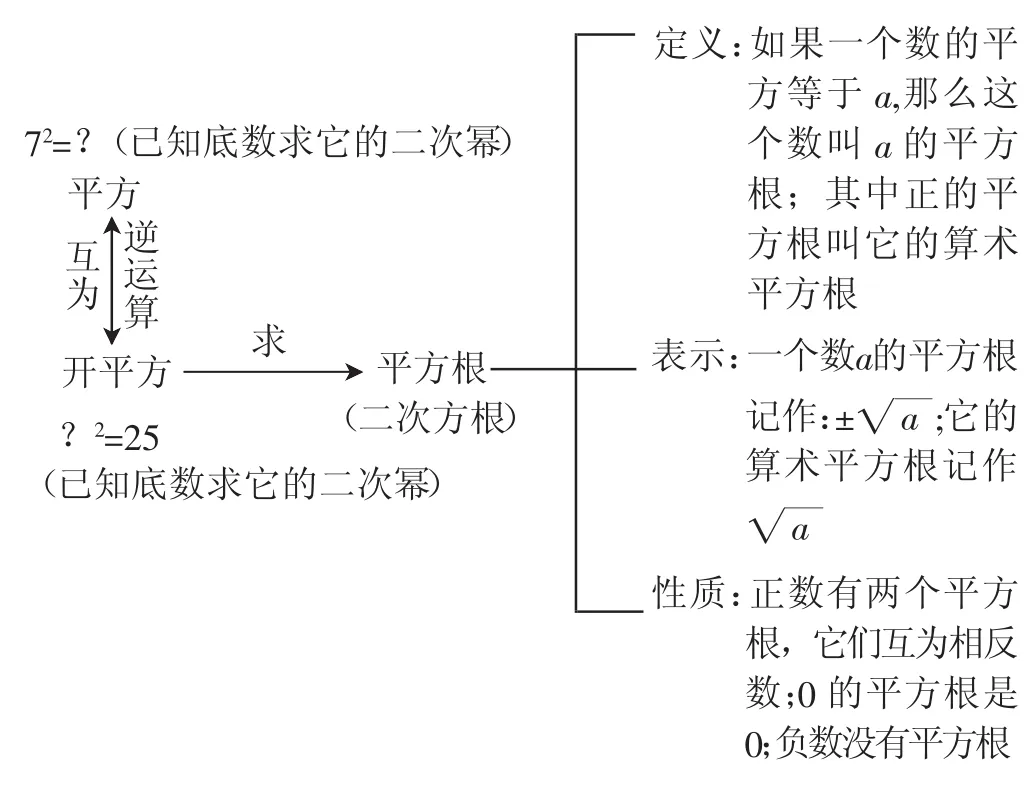
二、教学立意的进一步阐释

1.深刻理解教学内容，践行“学材再建构”

平方根的教学内容在当前不少版本的教材中都被不同方式呈现，有些教材是先由实际问题引入算术平方根，定义“根号”，然后第二课时再完善认知，定义平方根的概念.我们选择了基于第5种运算——乘方的逆运算出发，已知幂、指数，求底数的运算，定义了第6种运算——数的开方，并跟进定义了平方根及符号表示.这是基于深刻理解教学内容的观点，积极践行学材再建构，而不跟随教材亦步亦趋，从“教教材”走向了“用教材教”，追求了华东师大终师教授钟启泉先生所指出的“新旧教学的分水岭”.

2.适度联系实际情境，数的平方源自生活

数学史上有所谓的第一次数学危机，即无理数的发现.据说大数学家毕达哥拉斯有一个弟子——希帕索斯，正是发现无理数的人.他是在求正方形（边长为1）的对角线时，希帕索斯发起了愁，这到底是个什么数？根据老师所讲，“万数皆数”，“1是所有数的生成元”，“宇宙的一切都归结于整数和整数之比”，希帕索斯花了很长时间发现了这样的无理数，推翻了“万物皆数”的观点后，希帕索斯被教会囚禁起来，最终残忍地将他丢进大海，这是数学史上的一个悲剧.所以在数的开方教学时，适当引入一些实际情境，让学生感受到无理数与实际生活也是密切相关的.在上面的课例中，我们使用的最多的情境就是“已知正方形的面积，求正方形的边长”.

3.精心预设板书设计，乘方开方互逆运算

在近年来的《中学数学》（初中版）很多课例研究中，不但有教学流程的概述，还有板书设计的截图呈现，让我们受益甚大.在上文课例中，我们在最后也附出本课的板书设计，可以看出乘方与开方的逆运算关系，以及定义、符号表达等之间的关系.一个好的板书，不但要把新概念、新性质、新符号全部规范书写在“主板区”（通常在黑板的左侧），而且把具有关联的概念、性质或符号表达都用连接线恰当关联起来，以便让学生能一目了然，加深他们对数学概念之间的广泛联系的理解，同时像平方根的定义、表示、性质，还有平方根、数的开方与乘方之间的转化关系也得到揭示.顺便指出，在当前的现代化教学媒体面前，传统的板书设计有所弱化，特别是一些数学新授课全是PPT课件“翻来翻去”，一节课下来都没有板书，这种现象值得警惕.

三、写在后面

根据我们对不少学校数学教学的观察和了解，当前有一个现象：日常教学以习题单式的学案代替了教材，而开展教学研讨、示范课时，对教材又是亦步亦趋.这两种现象都值得思考，日常教学时“以题代书”，离开教材搞教学的现象让人担忧，而公开课、参赛课时，又不敢对教材进行“学材再建构”，怕被评课老师说起对教材的编写意图缺少理解等.想来，基于理解数学、理解学情积极开展“学材再建构”还有很长的路要走.

参考文献：

1.李庾南，祁国斌.自学·议论·引导：涵育学生核心素养的重要范式［J］.课程·教材·教法，2017（9）.

2.刘东升.悠然神会，妙处与君说——李庾南老师“平方根”课例赏析［J］.中国数学教育，2014（5）.

3.钟启泉.新旧教学的分水岭［J］.基础教育课程，2014（2）.

4.李功林.章起始课：精选问题，驱动全章进程——以“分式”章起始课为例［J］.中学数学（下），2017（12）.

5.郭锋.网络研讨，让全组老师分享听课意见——以一次学校数学组网络研讨活动为例［J］.中学数学（下），2017（12）.F