基于信息融合技术的结构损伤检测方法

井 立， 杨智春， 张甲奇

(1.西北工业大学 航空学院，西安 710072;2.中国飞行试验研究院 飞机所，西安 710089)

在结构服役过程中，载荷作用、疲劳与腐蚀效应、材料老化等因素会不可避免的造成结构的损伤，如果不能及时的检测和修复这些结构损伤，会严重影响到结构的安全性。近年来，基于振动的损伤检测方法得到了空前的发展，基于振动的损伤检测方法和思路不断涌现。文献[1]提出了互相关函数幅值向量(Cross Correlation Function Amplitude Vector，CorV)作为结构损伤检测的指标，可以检测出结构是否存在损伤以及损伤的位置。文献[2-3]在模态识别的自然激励法以及CorV的基础上提出了结构损伤检测的内积向量法(Inner Product Vector, IPV)，并通过层合复合材料梁损伤检测的仿真算例和蜂窝夹层复合材料梁的损伤检测实验验证了该方法的有效性和可行性。文献[4]提出以结构振动响应重构相空间的最小二乘距离(Least Square Distance, LSD)作为损伤因子来进行损伤检测。文献[5]中利用结构的加速度响应信号的频域能量作为损伤指标进行损伤检测，通过对大跨度桥梁结构的损伤检测，验证了这种方法可以准确检测出损伤位置。

在结构损伤检测的具体应用中发现，不同的损伤检测方法在对结构损伤状态的识别过程中，识别的精度不同，适用的结构也不相同，所以使用单一的损伤检测方法所获得的信息是不全面的，难以保证对结构损伤状态做出准确可靠的识别。近年来信息融合理论在结构损伤检测领域得到了广泛的应用[6]。文献[7]构造了模糊神经网络分类器，提出基于模糊神经网络的信息融合损伤检测方法。文献[8]提出了一种多故障特征信息融合的故障诊断方法,通过转子实验表明,多故障特征信息融合后的诊断结果可信度明显提高,充分验证了该融合诊断方法能够有效提高故障诊断的准确性和可靠性。文献[9]提出一种基于D-S证据理论的结构损伤检测方法。首先计算测量得到的每组数据的损伤基本概率分配函数(Basic Probability Assignment, BPA)，然后采用D-S证据理论将所有的BPAs进行融合得到最终的损伤检测结果。试验研究表明，通过融合所有的BPAs得到的损伤检测结果比任何单独得到的损伤检测结果都要更好。文献[10]利用信息融合技术识别结构的多位置损伤，采用了三种融合方法(Bayes理论、D-S证据理论和模糊聚合法)进行信息融合得到最终的决策结果。这几种方法都是在信息融合的决策层对损伤检查结果进行融合，本文研究的方法在特征层和决策层都进行了信息融合，从而得到最终的损伤检测结果。通过蜂窝夹层复合材料梁损伤检测试验对本文方法的有效性进行了验证，结构损伤识别的概率得到了进一步的提升。

1 信息融合方法

根据融合系统所处理的信息层次，信息融合常划分为数据层融合、特征层融合和决策层融合，如图1所示。在信息融合过程中，也可以在不同的融合层次中进行融合来得到最终结果。

(a)数据层融合

(b)特征层融合

(c)决策层融合

1.1 加权平均法

对于不同的损伤指标要选取不同的权值求解其加权平均值，目标是：加权平均得到的结果和各损伤指标之间欧氏距离的平方和达到最小。但是要达到这一目标，需要大量计算，耗费大量时间，不便于实际应用。本文采用下面的方法来选取各损伤指标的权值。

设融合前各损伤指标分别为Xi(i=1,2,…,n)，首先计算损伤指标的平均值

/n

(1)

然后计算各损伤指标分别到所有损伤指标平均值的欧氏距离

(2)

则定义各损伤指标的权值为

(3)

得到融合后的结果为

(4)

1.2 简单投票法

一个最直接的融合多种方法的策略是简单投票法(Simple Voting)，也称多数投票法(Majority Voting)[11]。如同投票选举一样，分为被选举者和选举者。投票规则是，每一选举者都为确定的被选举者投上一票，且仅此一票。最后，获票最多的被选举者胜出。

设M个选举者组成的集合为MS={mi|i=1,2,…,M}，T个被选举者组成的集合为TS={ti|j=1,2,…,T}，投票函数为

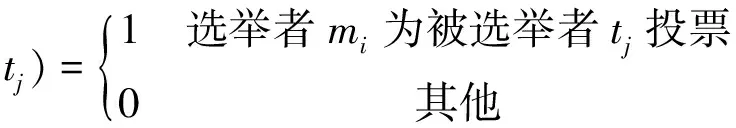
(5)

则被选举者tj的获票数为

,tj)

(6)

则根据被选举者tj所获票数的数据，决定出最后的胜出者

(7)

1.3 D-S证据理论

D-S证据理论[12]为不确定信息的表达和合成提供了一种强有力的方法，特别适用于决策层的信息融合。

设Ω是样本空间，Ω由一个互不相容的陈述集合组的幂集2Ω构成命题集合，φ为空集。

设函数m满足下列条件的映射

m: 2Ω→[0,1]

(8)

(1)不可能事件的基本概率是0，即m(φ)=0；

(2)2Ω中全部元素的基本概率之和为1，即

(9)

式中:m为2Ω上的概率分配函数，m(A)称为A的基本概率数，表示对A的信任度。

设Bel1和Bel2为同一识别结构上的信任度函数，m1和m2分别为对应的概率分配函数，则正交和m=m1+m2为

m(φ)=0

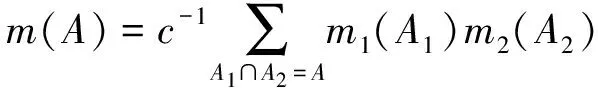
(10)

式中：

如果c≠0，则正交和m也是一个概率分配函数；如果c=0，则不存在正交和m，此时m1和m2矛盾。

2 结构损伤检测结的信息融合

首先对几种损伤检测方法进行简单的介绍：

(1)Corv法将参考点的响应信号和各个测量点的响应信号的互相关函数的最大值作为损伤因子进行结构损伤检测；

(2)IPV法将参考点的响应信号和各个测量点的响应信号的内积值作为损伤因子进行结构损伤检测；

(3)重构相空间法是将所有测量点的响应信号重构到相空间并得到最小二乘距离作为损伤因子进行结构损伤检测；

(4)加速度响应能量法是根据各个测量点的加速度响应信号求出响应能量作为损伤因子进行结构损伤检测。

采用信息融合法对结构进行损伤检测，主要分为三个步骤：

(11)

步骤2:引入判断结构是否发生损伤的阈值It，如果损伤指标的所有元素均小于It，则结构没有损伤发生，若损伤指标存在元素大于It则认为结构有损伤发生。损伤阈值利用D′的均值和标准差来确定

It=μ+αcσ

(12)

步骤3:当“步骤2”判断出结构发生损伤后，接下来需要判断的是结构发生损伤的位置。在此提出损伤概率指标，可以计算出各区域发生损伤的概率。

定义结构的损伤概率指标

(13)

计算出结构发生损伤的概率后，再通过D-S证据理论对其进行融合，得到各个区域发生损伤的融合结果，即结构各个区域发生损伤的概率。

结构损伤检测过程中信息融合的具体流程，如图2所示。

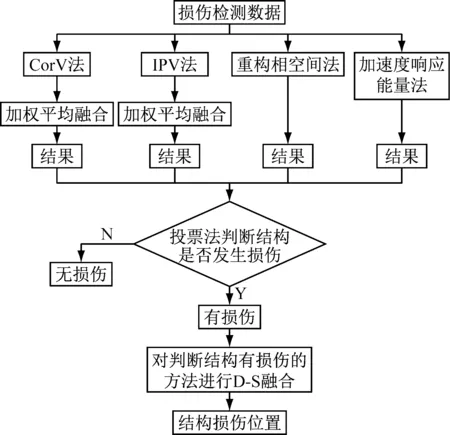
图2 损伤检测信息融合流程图

3 蜂窝夹层复合材料悬臂梁的损伤检测

试验使用的蜂窝夹层复合材料悬臂梁的几何尺寸为400 mm×40 mm×16 mm(长×宽×厚)，蜂窝夹层复合材料为六边形铝蜂窝，上、下面板为层合碳纤维复合材料板。试验中，在梁宽度方向的中轴线上沿长度方向间隔50 mm等间距布置8个测点，如图3所示。用加速度计测量梁的振动加速度响应，利用非接触式电磁激振器在梁的自由端下面板中点处进行激励，图4为试验布置。在蜂窝夹层梁上面板与蜂窝芯黏结处，人工将面板与芯层的黏结层切开，制造出贯穿梁宽度的脱黏损伤。

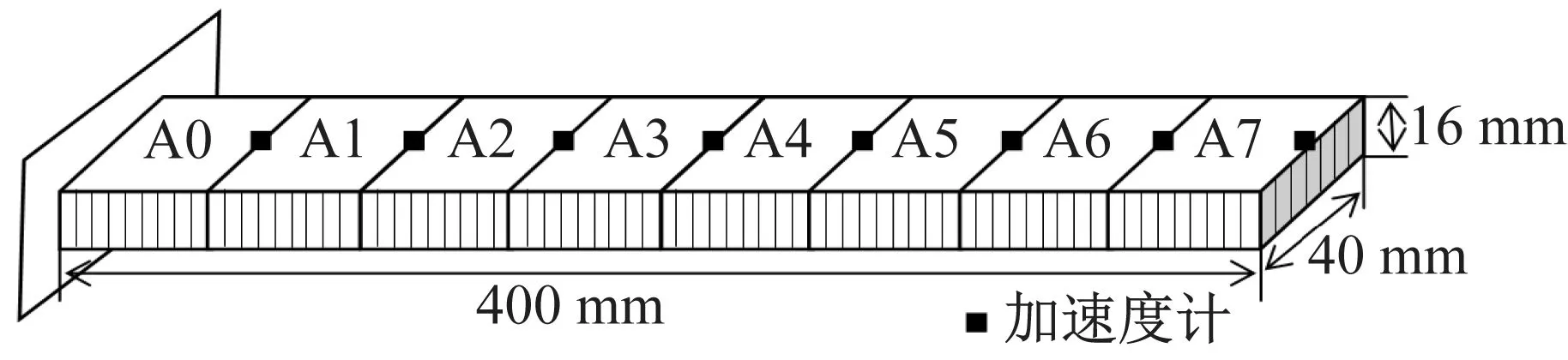
图3 复合材料梁加速度测点

为了试验验证本文方法对损伤位置检测的有效性，使用三根相同的蜂窝夹层复合材料悬臂梁，分别命名为B1、B2和B3，模拟3种不同的损伤工况，具体的损伤模式，如表1所示。

图4 试验布置

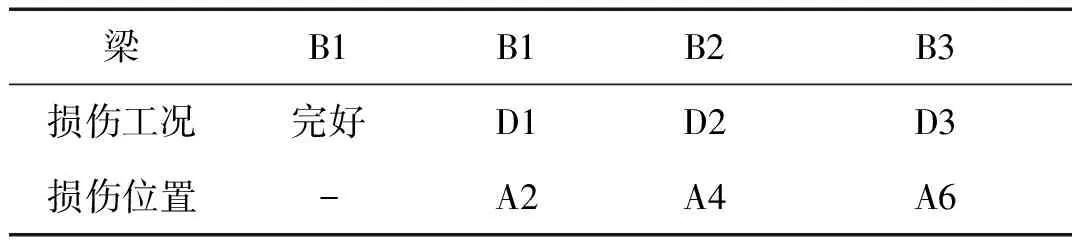
梁B1B1B2B3损伤工况完好D1D2D3损伤位置-A2A4A6

完好结构的损伤检测结果,如图5所示。图5(a)为选取不同参考点得到的IPV的损伤检测结果，采用加权平均法对不同参考点得到的损伤指标进行融合，得到加权平均融合后的损伤指标;图5(b)为选取不同参考点得到的CorV损伤检测结果，采用加权平均法对不同参考点得到的损伤指标进行融合，得到加权平均融合后的损伤指标；从图5(a)、图5(b)和图5(c)可知,各损伤指标的所有元素都小于各自对应的阈值，加速度响应能量法的损伤指标存在元素大于其阈值，则三种方法判断结构没有发生损伤，一种方法判断结构发生损伤，通过简单投票法得到蜂窝夹层复合材料梁结构未发生损伤，与实际情况相符。

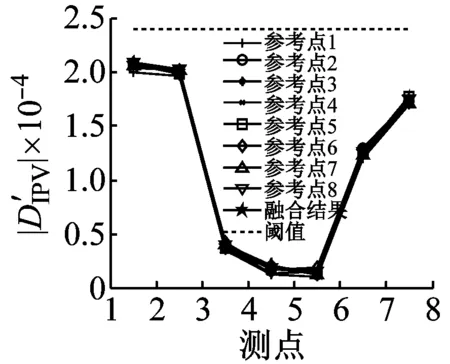
(a) IPV法

(b) CorV法

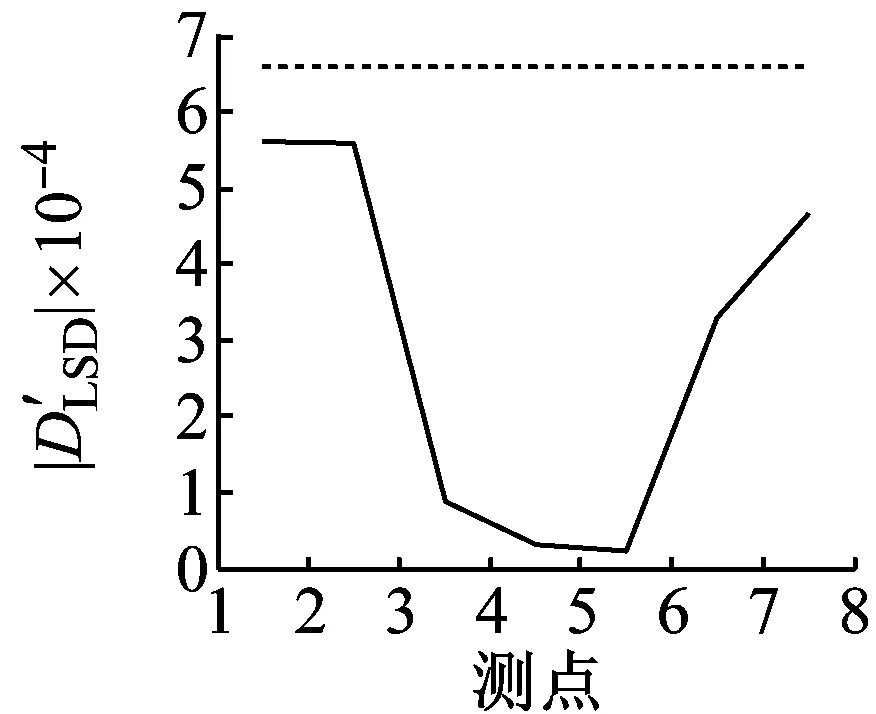
(c) 重构相空间法

(d) 加速度响应能量法

D1工况的损伤检测结果,如图6所示。IPV法经过加权平均融合后的损伤指标、CorV法经过加权平均融合后的损伤指标和重构相空间法的损伤指标均有元素大于其阈值，而加速度响应能量法的损伤指标所有元素都小于其阈值，则三种方法判断结构发生损伤，一种方法判断结构未发生损伤，通过简单投票法认为结构发生了损伤。再将这三种方法得到的损伤指标进行概率化，采用D-S证据理论进行融合得到的结果，如图6(e)所示。从图6(e)中可知,在测点2、测点3之间(即区域A2处)蜂窝夹层复合材料梁结构发生损伤的概率最大，与实际损伤情况相符，由此可知,采用单种方法得到该区域的损伤概率值最大为0.43，而融合后该区域的损伤概率值为0.94，融合后得到损伤概率明显大于采用单一方法得到的损伤概率。

(a) IPV法

(b) CorV法

(c) 重构相空间法

(d) 加速度响应能量法

(e) D-S证据理论的融合结果

D2工况的损伤检测结果,如图7所示。IPV法融合后的损伤指标、CorV法融合后的损伤指标、重构相空间法的损伤指标和加速度响应能量法的损伤指标均有元素大于各自对应的阈值，则四种损伤检测方法都判断结构发生损伤，通过简单投票法认为结构发生损伤。进行概率化后采用D-S证据理论融合方法得到图7(e)中的融合结果。从图7(e)可知,在测点4、测点5之间(即区域A4处)蜂窝夹层复合材料梁结构发生损伤的概率最大，与实际损伤情况相符，且融合后该区域的损伤概率值已经接近于1，明显大于采用单种方法得到的损伤概率。

(a) IPV法

(b) CorV法

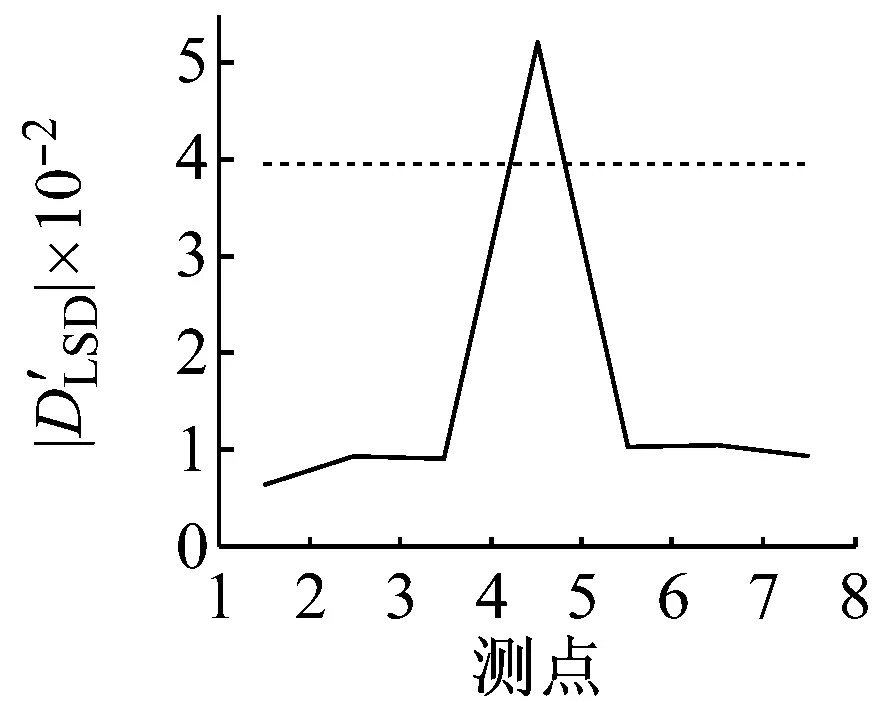
(c) 重构相空间法

(d) 加速度响应能量法

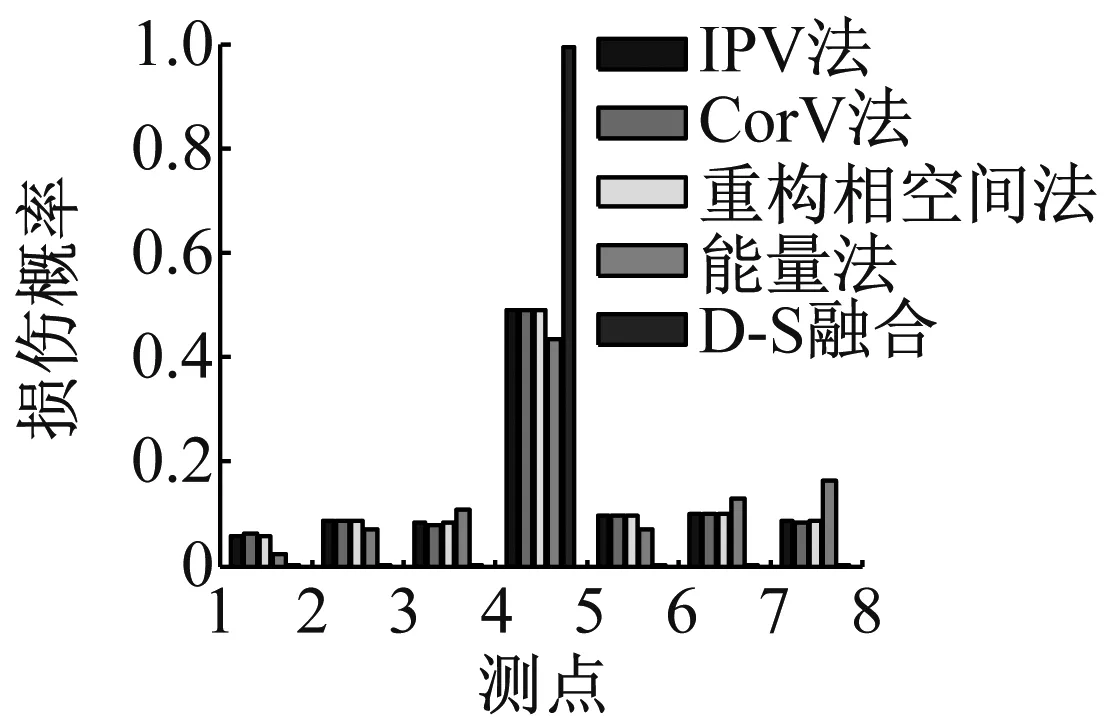
(e) D-S证据理论的融合结果

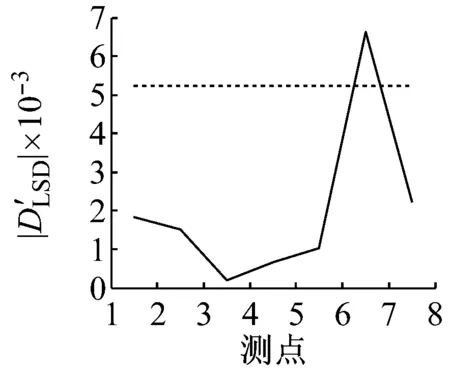
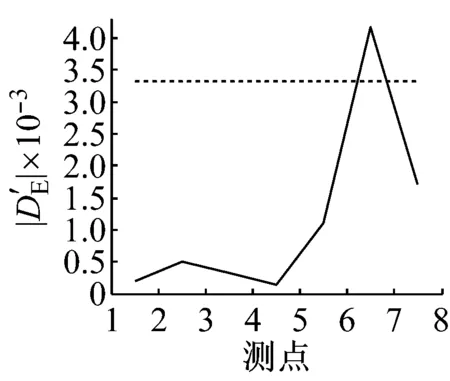
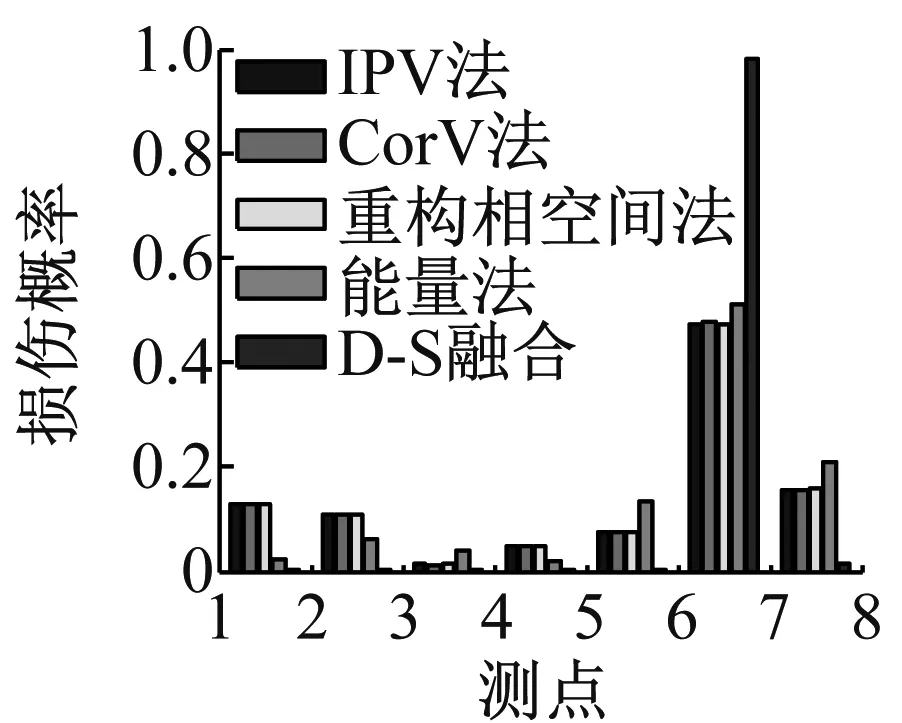
D3工况的损伤检测结果，如图8所示。四种损伤检测方法均认为结构发生损伤，通过简单投票法得到结构发生损伤，再对损伤指标进行概率化后采用D-S证据理论融合得到图8(e)中的融合结果。由图8(e)可知，在测点6、测点7之间 (即区域A6处)蜂窝夹层复合材料梁结构发生损伤的概率为0.98，明显大于采用单种方法得到的损伤概率。

蜂窝夹层复合材料梁损伤检测实验说明，在结构损伤检测中，采用信息融合的方法可以准确的判断出结构是否发生了损伤以及发生损伤的位置，且得到的损伤位置发生损伤的概率明显大于任何其他方法单独得到的损伤概率。

4 结 论

本文将信息融合方法应用在结构损伤检测当中并通过蜂窝夹层复合材料梁结构的损伤检测试验，验证了在结构损伤检测过程中使用信息融合技术的可行性和有效性，从损伤检测结果中可以看到:

(1)采用信息融合技术可以准确地判断出结构是否发生了损伤以及发生损伤的位置，得到的结果更加的准确、可信。

(2)判断结构是否发生损伤时，采用单一的损伤检测方法可能会导致误检和漏检，通过简单投票法对不同方法得到的结果进行融合，使结构损伤检测的结果的更加准确。

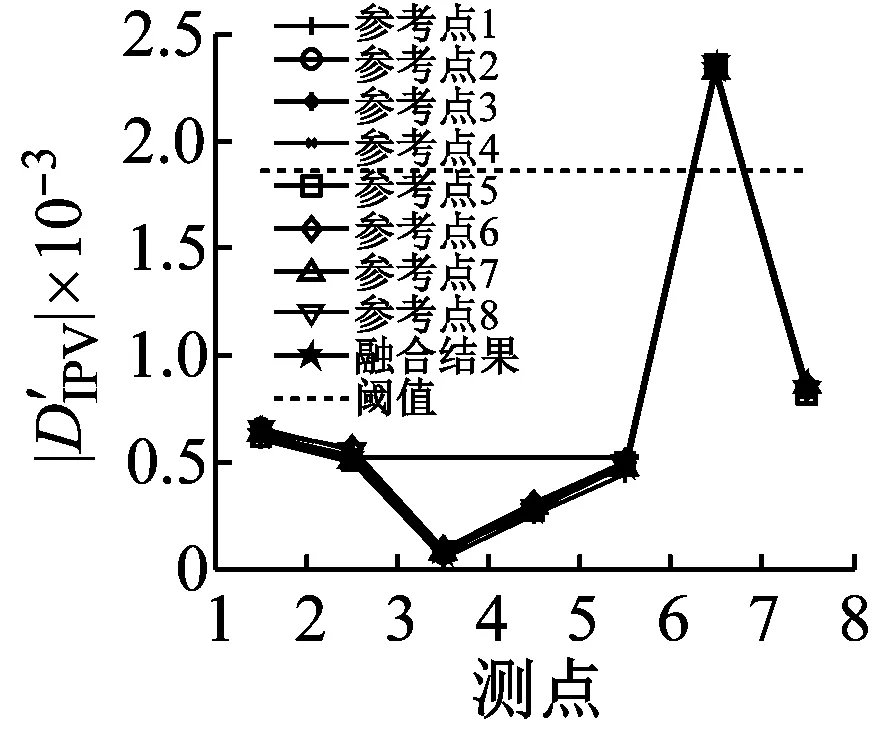
(a) IPV法

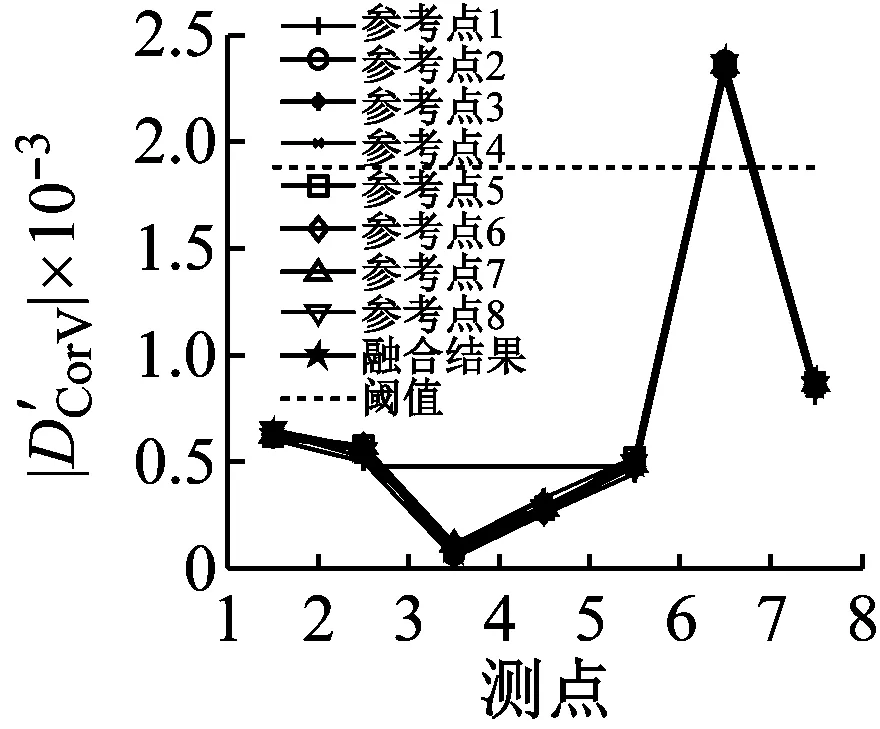
(b) CorV法

(c) 重构相空间法

(d) 加速度响应能量法

(e) D-S证据理论的融合结果

(3)在判断结构发生损伤后，对各种结构损伤检测方法得到的结果采用D-S证据理论进行融合，判断结构区域发生损伤的概率，从结果中可以看到：融合后得到损伤区域损伤的概率比任何一种方法单独得到的损伤概率都要更大。

[1] YANG Zhichun, YU Zhefeng, SUN Hao. On the cross correlation function amplitude vector and its application to structural damage detection[J]. Mechanical Systems and Signal Processing, 2007, 21(7): 2918-2932.

[2] WANG Le, YANG Zhichun, WATERS T P. Structural damage detection using cross correlation functions of vibration response[J]. Journal of Sound and Vibration, 2010, 329(24): 5070-5086.

[3] YANG Z C, WANG L, WANG H, et al. Damage detection in composite structures using vibration response under stochastic excitation[J]. Journal of Sound and Vibration, 2009, 325(4): 755-768.

[4] 井立. 结构损伤检测的信息融合方法[D]. 西安：西北工业大学，2015.

[5] XU Z D, WU Z. Energy damage detection strategy based on acceleration responses for long-span bridge structures[J]. Engineering Structures, 2007, 29(4): 609-617.

[6] 姜绍飞, 王留生, 殷晓志, 等. 结构健康监测中的数据融合技术[J]. 沈阳建筑大学学报(自然科学版), 2005, 21(1): 18-22.

JIANG Shaofei,WANG Liusheng,YIN Xiaozhi,et al. Data fusion technology in structural health monitoring[J].Journal of Shenyang Jianzhu University (Natural Science)，2005,21(1):18-22.

[7] 姜绍飞, 张帅. 基于模糊神经网络的数据融合结构损伤识别方法[J]. 工程力学, 2008, 25(2): 95-101.

JIANG Shaofei, ZHANG Shuai.Structural damage identification method with data fusion of fuzzy neural network[J]. Engineering Mechanics, 2008, 25(2): 95-101.

[8] 谭青, 向阳辉. 加权证据理论信息融合方法在故障诊断中的应用[J]. 振动与冲击, 2008, 27(4): 112-116.

TAN Qing, XIANG Yanghui. Application of weighted evidence theory information fusion method in fault diagnosis[J]. Journal of Vibration and Shock, 2008, 27(4): 112-116.

[9] BAO Y, LI H, AN Y, et al. Dempster-Shafer evidence theory approach to structural damage detection[J]. Structural Health Monitoring, 2012,11(1):13-26.

[10] GUO H Y. Structural damage detection using information fusion technique[J]. Mechanical Systems and Signal Processing, 2006, 20(5): 1173-1188.

[11] CHAN P K, STOLFO S J. A comparative evaluation of voting and meta-learning on partitioned data[C]//ICML. 1995: 90-98.

[12] SHAFER G A, SHAFER G. A mathematical theory of evidence[M]. Princeton: Princeton University Press, 1976.