π型断面超高斜拉桥涡振减振措施风洞试验研究
李 欢, 何旭辉, 王汉封, 刘梦婷, 彭 思
(1. 中南大学 土木工程学院, 长沙 410075; 2. 中南大学 高速铁路建造技术国家工程试验室, 长沙 410075)
1955年第一座现代斜拉桥——斯曹姆松特桥建成至今,斜拉桥因其结构简单、受力明确、造型优美、施工方便、跨越能力强而得到了长足的发展[1]。随着斜拉桥跨度的进一步增加,为减轻结构自重,降低造价,适应复杂地区的施工条件,π型断面主梁结构形式在斜拉桥建造过程中得到了广泛的应用,特别是公路桥梁。π型断面是满足构造要求最经济的斜拉桥主梁断面形式之一,尤其是地形复杂施工困难的多山地区。但对于山区大跨度超高斜拉桥而言,其气动稳定性较差,很容易产生较大幅度的涡激振动。虽然涡激振动是一种限幅振动,不会导致桥梁发生毁灭性的破坏,但较大幅度的振动会引起结构的疲劳损伤,缩短结构寿命,降低桥上行人和车辆的舒适性[2-4],同时还可能引起其它灾难性的气动不稳定振动。π型断面斜拉桥的涡激振动现象已经引起人们的广泛关注[5-7]。
为使π型梁在大跨度桥梁中安全使用,常常需要一定的减振措施来优化其气动特性,使其满足抗风要求。目前减振措施主要分为三类,即结构措施、阻尼措施和气动措施[8]。结构措施复杂且实施难度大而较少采用;阻尼措施造价高、实际工程中维护困难也较少采用;气动措施工作稳定可靠、维护简单和安装方便已成为目前抑制涡振最常用的方法。Kubo等[9]针对简化的π型断面通过调整边主梁的中心间距和桥面附属设施的高度及边主梁距主梁边缘的距离提出了详细的优化方案,并通过识别主梁气动阻尼和流场显示解释了该措施的减振机理,但无法为已完成初步设计的桥梁提供参考;Irwin[10]通过节段模型风洞试验和现场实测对比研究,采用竖向稳定板成功抑制了塞文二桥的涡激振动;张志田等[11]采用稳定板将某开口断面斜拉桥的涡激振幅控制在规范允许的范围内,但未对稳定板的抑振规律进行系统研究;颜宇光等[12]研究了风嘴、导流板、稳定板、扰流板及其组合等多种气动减振措施对开口断面斜拉桥涡振控制效果,但无通用性的减振规律;杨光辉等[13]借助CFD(Compotational Fluid Dynamics)仿真技术分析了下中央稳定板的减振机理,但数值模拟效果一般。由以上文献研究结果可知,各种减振措施的减振效果参差不齐、通用性差,且减振机理尚不明确;不同桥梁使用同种减振措施抑振效果可能有较大差异;因此针对某一具体桥梁仍需进行详细的研究,尤其是风场环境复杂、结构新颖的大跨度桥梁。
本文针对某拟建山区大跨度超高π型主梁断面斜拉桥,通过节段模型试验,分析比较了隔流板和下稳定板等气动措施对施工阶段π型主梁断面涡激振动性能的影响,并提出了改善涡激振动性能的抗风措施。最后结合数值模拟的方法对涡振发生及减振措施的机理进行了初步探讨。为同类型桥梁提供参考。
1 工程背景
某拟建山区大跨度超高斜拉桥为三塔双索面叠合梁斜拉桥。桥梁跨径布置为(249.5+550+550+249.5) m,全桥总长为1 599 m。三塔高度分别为320 m、328 m和298 m,中塔仅比法国米约大桥最高塔低15 m,属世界第二,但该桥桥塔一次施工完成。桥面与河流平均水位垂直距离高达292.30 m。该桥主梁为π型梁,梁宽30.20 m,高3.58 m,宽高比为8.44;边主梁高2.92 m,主梁悬挑长度2.25 m;除去断面的悬挑长度,断面的宽高比约为7.18;整桥布置及主梁断面,如图1所示。施工阶段最大双悬臂状态塔高328 m,悬臂长度为270 m。

(a) 立面图和平面图(cm)

(b) 标准主梁断面图(mm)
2 节段模型涡激振动试验
2.1 试验设置
试验在中南大学风洞试验室高速试验段进行,该试验段的几何尺寸为长×宽×高=15.0 m×3.0 m×3.0 m,试验风速在0~94 m/s范围内连续可调,湍流度小于0.3%,速度场不均性小于0.5%。试验来流为均匀流。
根据实桥尺寸、风洞断面尺寸及规范要求,选取节段模型的缩尺比为1:40,模型采用加厚ABS板制作而成以保证其刚度要求,节段模型严格模拟了实桥的气动外形,模型试验参数,如表1所示。节段模型弹性悬挂布置,如图2所示。
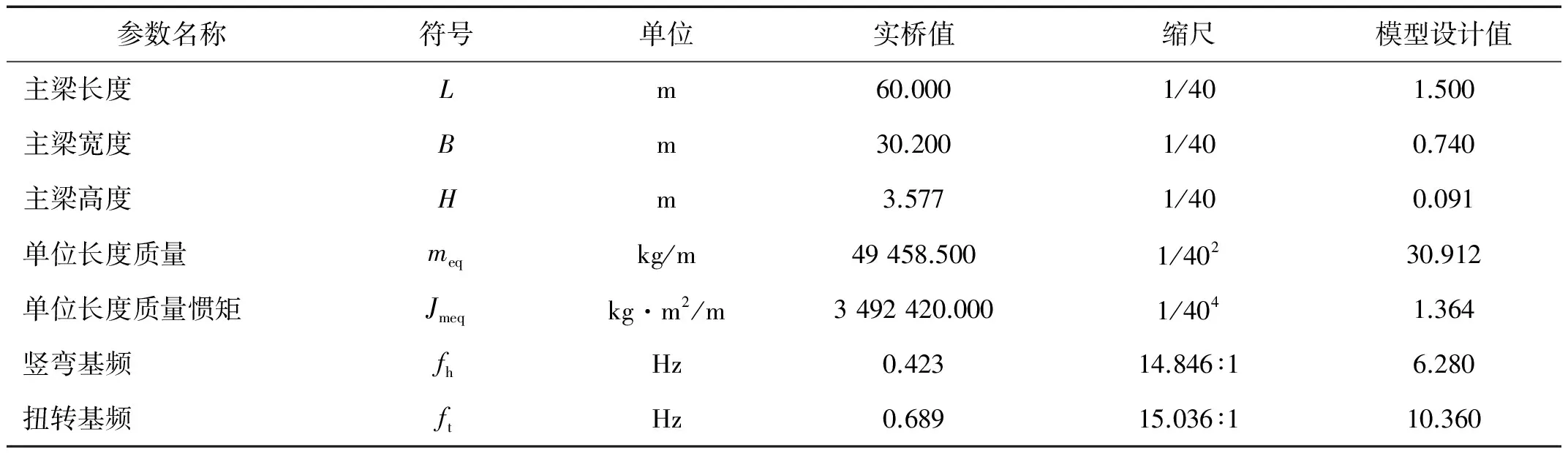
表1 节段模型试验参数

图2 节段模型弹性悬挂状态
试验采用KEYENCE(LK-G150)激光位移计,其测量精度为0.04 mm。两个激光位移计对称布置在模型上下游,如图2所示,通过同步测试获得模型振动响应信号。试验采样频率为2 000 Hz,采样时间为25 s。
2.2 试验工况及减振措施
为研究主梁涡振性能及隔流板和下稳定板两种不同的气动减振措施的减振效果,分别进行了不同风攻角下原始断面、增设隔流板和增设下稳定板主梁断面的涡振试验。试验工况,如表2所示。隔流板和下稳定板两种不同的气动减振措施及安装位置,如图3所示。为保证试验结果准确性,各减振措施均采用3 mm厚的ABS板由电脑雕刻而成,使其能与模型较好的契合。气动措施几何尺寸分别用边主梁下翼缘宽度l=1.20 m和边主梁高度h=2.92 m来无量纲化。

(a) 隔流板

(b) 下稳定板

主梁断面气动措施尺寸风攻角/(°)试验阻尼比/%竖弯扭转原始断面-00.8600.841增设隔流板0.67l00.8730.8460.83l00.8730.8461.00l00.8730.846增设两道下稳定板0.48h-30.8620.8430.74h-30.8620.8431.10h-30.8620.8431.10h00.8620.8431.10h30.8620.843
3 结果及分析
3.1 无减振措施试验结果分析
针对图1所示,施工阶段标准主梁断面进行0°风攻角的测试。由于该桥主梁为钢-混叠合梁,依据规范[14]要求,试验阻尼比的范围为0.900%~1.100%。试验时先采用较小的阻尼比,找到涡激共振锁定风速区间,然后调整竖弯阻尼比为0.860%,扭转阻尼比为0.841%;由于桥位风场环境复杂,桥塔高,最大悬臂长度大,因而采用了比规范稍小的阻尼比,使试验结果偏安全。采用文献[15]提供的计算公式将试验结果换算到实桥,得到该桥的竖向涡振位移最大振幅修正系数为CV=1.61,扭转涡振位移最大振幅修正系数为CT=1.85。并根据有限元模型动力计算结果由规范计算出实桥竖向涡激振动的允许振幅为[ha]=0.095 m,扭转涡激振动的允许振幅为[θa]=0.219°。为了便于和规范限值比较,所有试验结果均采用式(1)和式(2)来无量纲化,其中Chc为竖弯无量纲振幅,Cθc为扭转无量纲振幅。
Chc=hc/[ha]=hc/0.095
(1)
Cθc=θc/[θa]=θc/0.219
(2)
图4给出了换算到实桥的主梁振动位移随风速变化曲线。由图4可知,施工阶段0°风攻角风速16~23 m/s时出现了明显的竖向涡激振动,最大振幅为规范限值的2.39倍;但无明显的扭转涡激振动。对涡振锁定风速下模型的位移时程曲线进行频谱分析,如图5所示。可见模型竖向涡振频率与模型卓越频率一致,均为6.280 Hz。
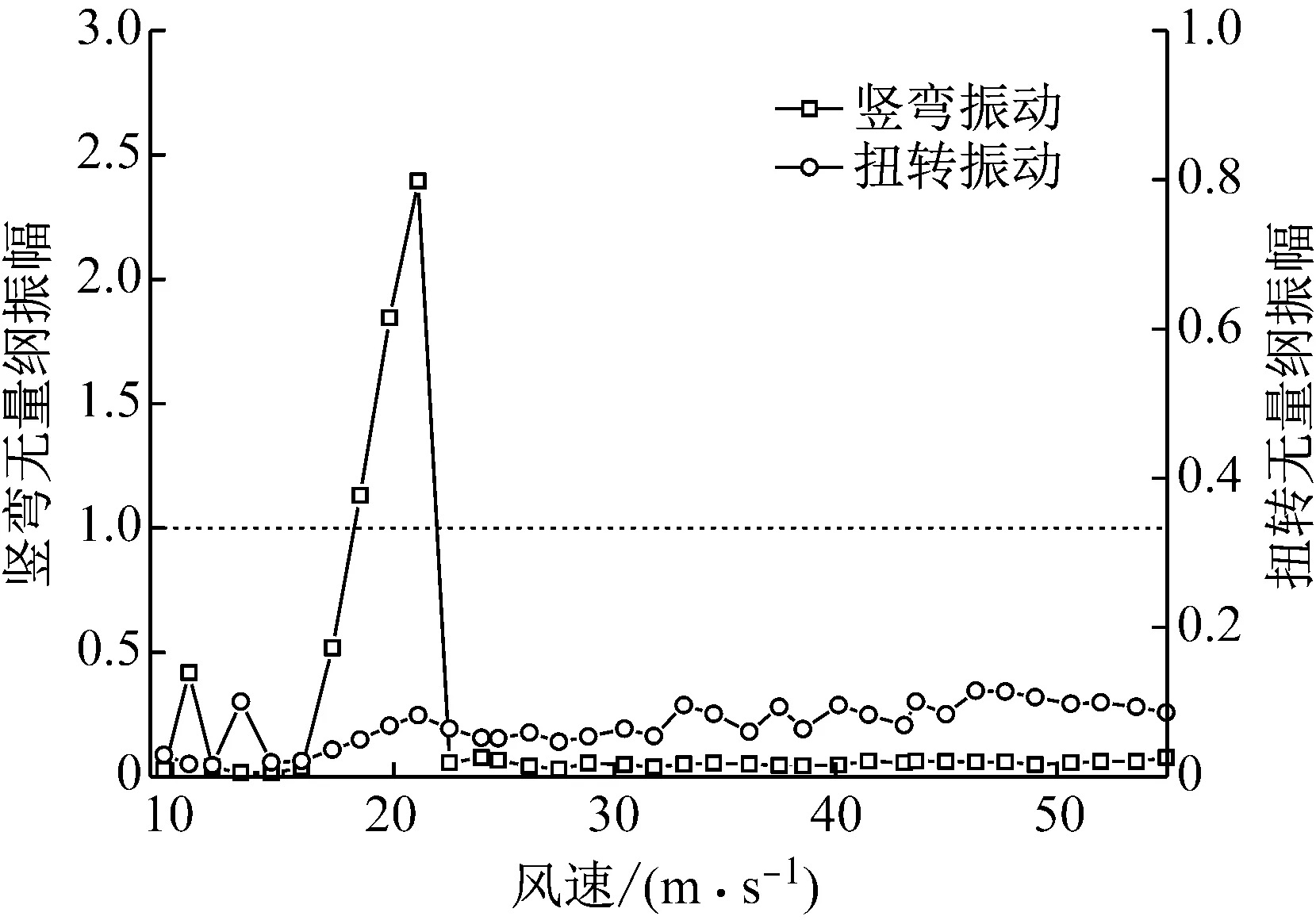
图4 0°风攻角无抗风措施主梁涡振试验结果

图5 无抗风措施主梁竖向涡激振动频谱图
3.2 减振措施试验结果分析
根据表2所列减振措施在0°风攻角下进行了三种宽度隔流板的涡振试验,在-3°风攻角下进行了三种长度两道下稳定板的涡振试验。图6为0°风攻角增设不同宽度的隔流板主梁振动位移随风速变化曲线。由图6可知,增设隔流板后主梁竖向涡振振幅降低了35%~50%,最大振幅仍超规范限值;随着隔流板宽度的增大,其减振效果趋于稳定,涡振起振风速逐渐降低,但锁定风速区间大小几乎保持不变,且对扭转涡振几乎没有影响。
图7为-3°风攻角增设两道不同长度的下稳定板主梁振动位移随风速变化曲线。由图7可知,增设两道下稳定板后,主梁竖向涡振振幅明显减小。随着下稳定板长度的增加,其减振效果愈加显著;当下稳定板的长度增加到边主梁高度的1.10倍时,竖向涡振振幅下降了80%左右,较好的抑制了主梁竖向涡激振动;然而随着下稳定板的增长,主梁扭转涡振幅值逐渐增大,但振幅峰值仍满足规范限值要求。
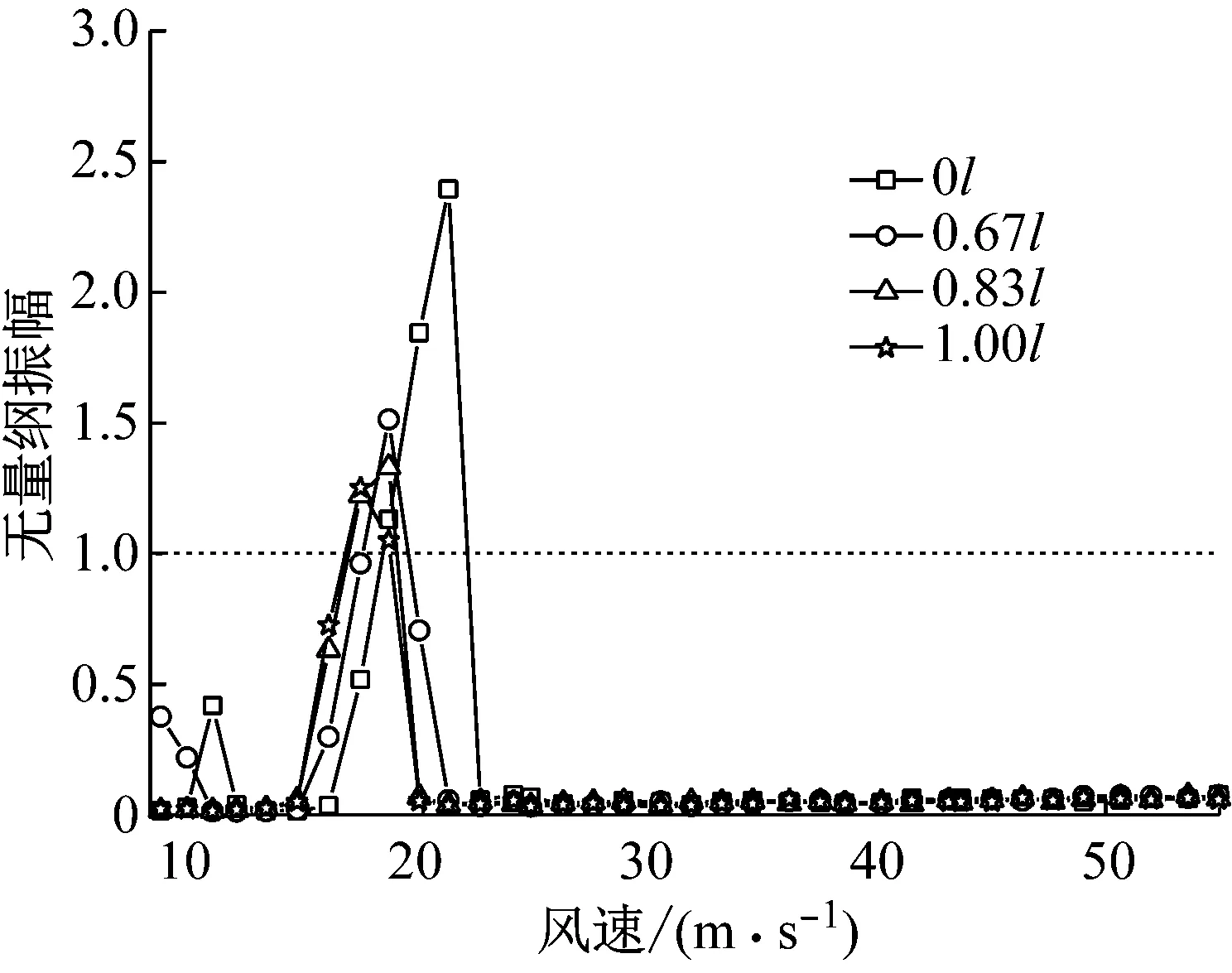
(a) 竖向振动位移幅值

(b) 扭转振动位移幅值
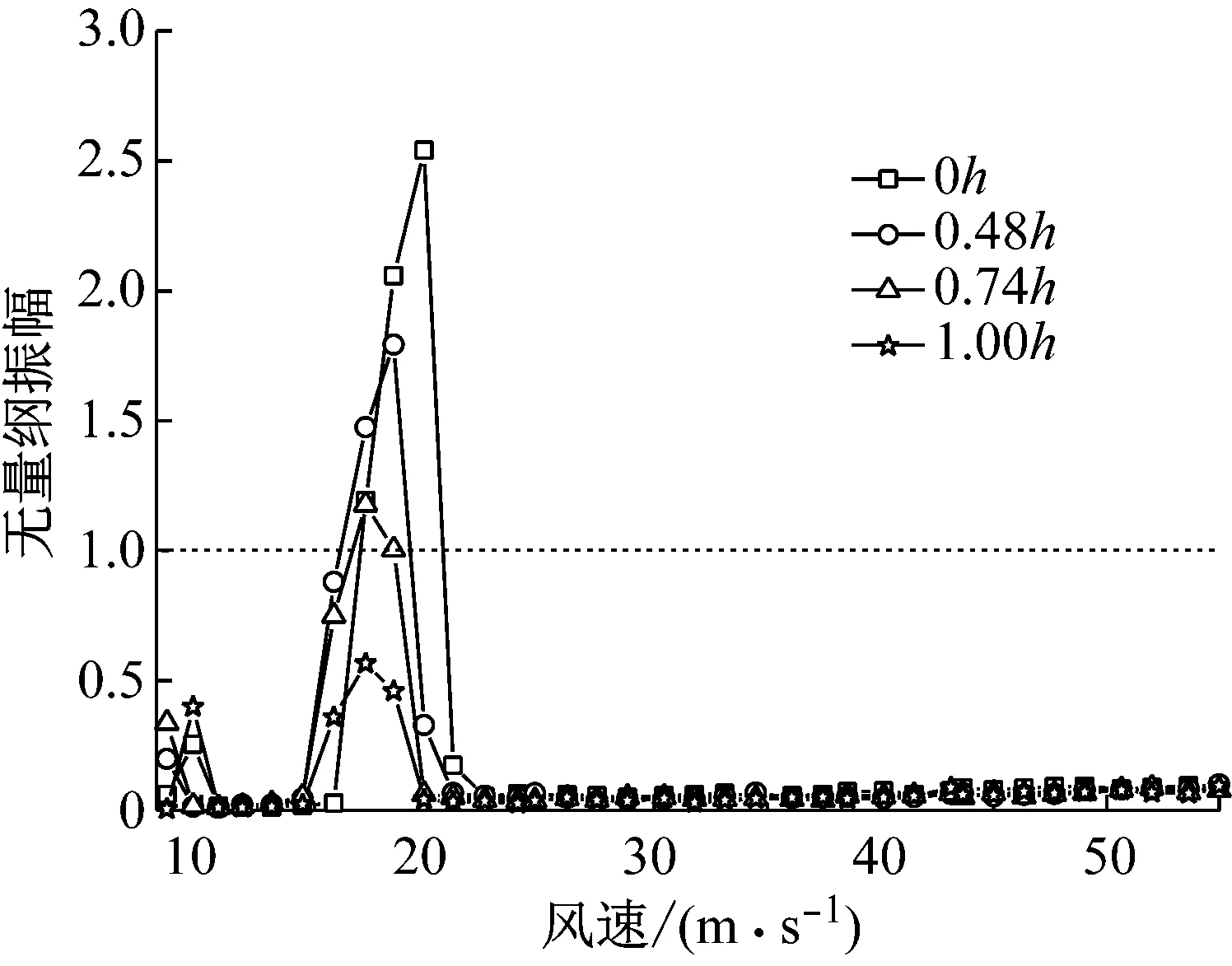
(a) 竖向振动位移幅值
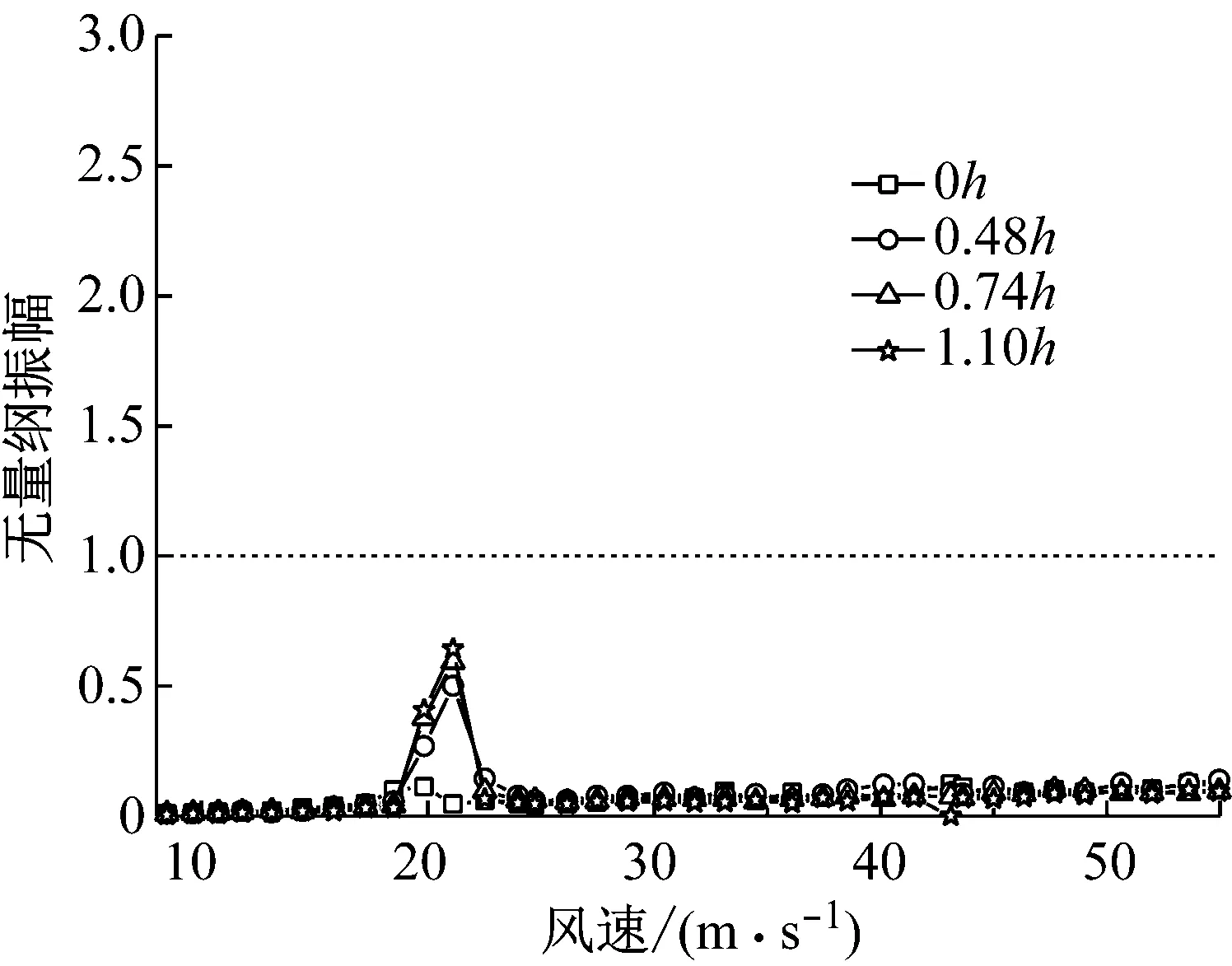
(b) 扭转振动位移幅值
图8为不同风攻角增设两道1.10h的下稳定板主梁振动位移随风速变化曲线。由图8可知,各攻角下主梁仍存在涡激共振现象,但振幅峰值均小于规范限值;虽然增设两道1.10h的下稳定板后主梁颤振临界风速由82.37 m/s下降到79.23 m/s,但仍满足规范颤振检验风速45.67 m/s的要求;因此施工阶段可选取两道1.10h的下稳定板作为气动减振措施。图8表明涡激共振对风攻角较为敏感,-3°攻角下稳定板的减振效果最差,这为上文不同长度的下稳定板选取-3°攻角进行风洞试验提供了依据。攻角的变化不改变涡振锁定风速区间的大小,但改变涡振起振风速的大小,随攻角的增大起振风速有增大的趋势。

(a) 竖向振动位移幅值

(b) 扭转振动位移幅值
4 涡振机理初步探讨
0°风偏角下将π型主梁断面简化为二维断面进行数值模拟已得到大家的认可[16-17],本次模拟采用类似方法。在FLUENT(16.0)CFD中使用SSTk-ω湍流模型,入口为速度边界,出口为press-outlet边界,桥梁表面为无滑移固体壁面边界,计算域顶面、底面均为对称界面。模型宽0.740 m、高0.091 m,计算域宽10 m、高5 m,模型形心位于距入口3.5 m的计算域中央。计算域采用结构化网格,在壁面处进行了加密处理,计算域及网格设置,如图9所示。

(a) 计算域总体网格
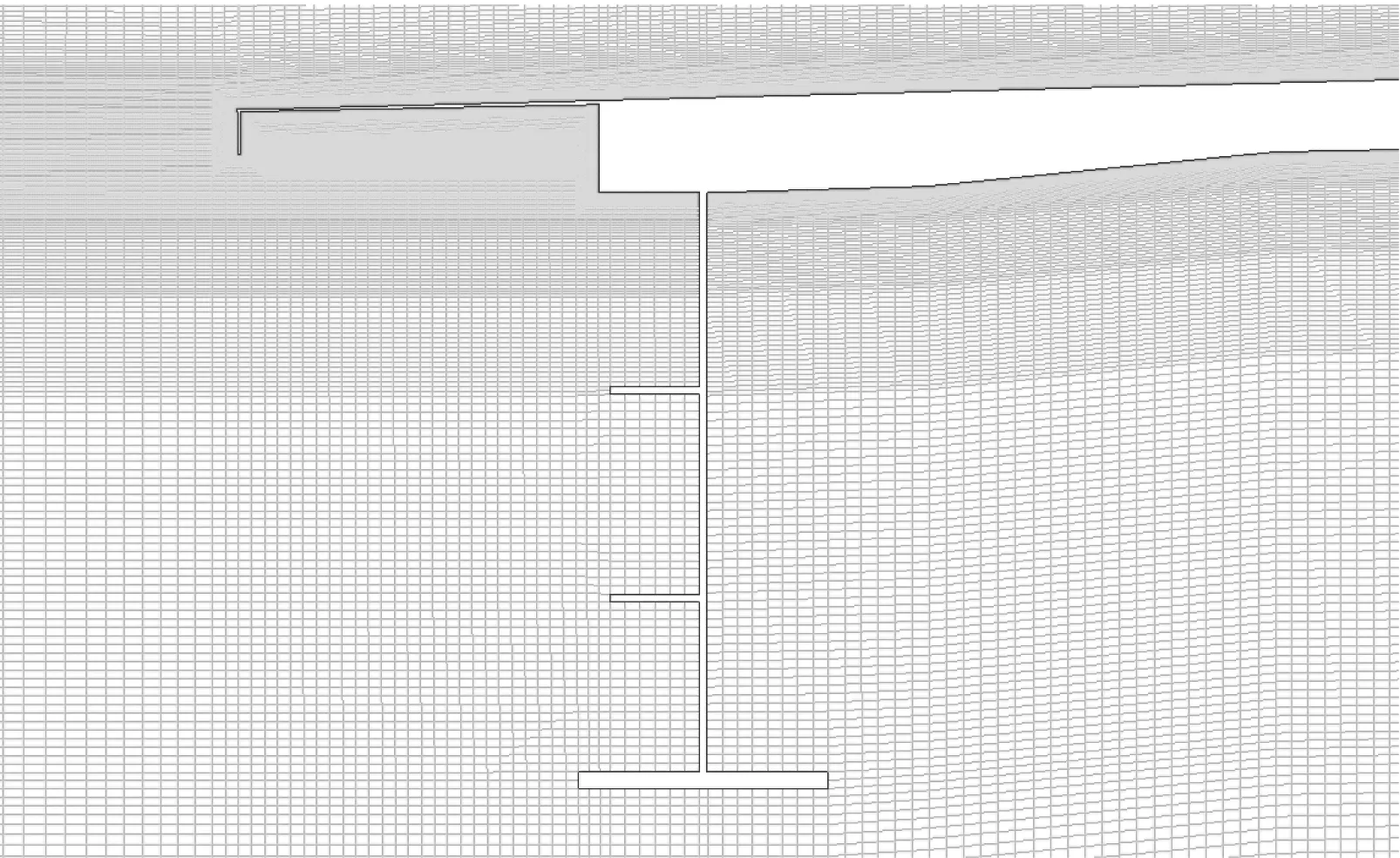
(b) 近壁面处局部加密网格
涡振锁定风速下0°风攻角时原始断面周围瞬时涡量如图10所示。由图10可知,与Shimada等[18]计算的宽高比为7的矩形断面周围涡量图类似;且两者的雷诺数分别为4.8×104和2.2×104,具有较高的可比性。该状态下模型升力时程曲线,如图11所示。数值计算升力系数平均值与风洞试验值0.09能较好地吻合。由以上对比分析结果可知,本次数值计算能够较准确地模拟断面周围的扰流特征。

图10 断面周围瞬时涡量图
Fig.10 Instantaneous vorticity contours around the section
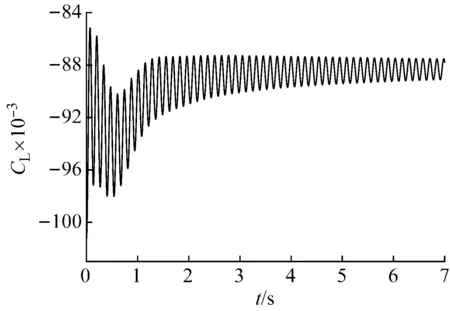
图11 升力系数时程
各计算工况来流风速均为涡振锁定风速,且采用来流风速对流场进行无量纲化。图12为原始断面平均流场风速矢量图。由图12可知,上表面气流在模型迎风边缘分离,形成一个较小旋涡,并在模型上表面中部位置再附;下表面气流在上游边主梁下翼缘分离并部分附着在下游边主梁的下翼缘上,在模型下部形成一个较大旋涡;下表面分离泡在上游边主梁下翼缘形成并发展壮大,结合图10可知,下表面旋涡结构经过下游边主梁下翼缘进入尾涡区。

图12 原始断面风速矢量图
图13为增设1.00l宽度的隔流板后主梁断面平均流场风速矢量图。与图12对比分析可知,增设隔流板前后断面下表面旋涡结构略为减小,前后边主梁内侧均有小旋涡产生,下表面负压值略有增大;上表面压力场几乎保持不变;虽然模型弹性悬挂时存在明显的流固耦合作用,断面绕流特性会有一些差异,但隔流板无法改变下表面旋涡结构是其不能较好抑制涡振的主要原因。

图13 增设1.00l隔流板断面风速矢量图
图14为不同风攻角增设两道1.10h长度的下稳定板后主梁断面平均流场风速矢量图。与图12、图13对比分析可知,0°风攻角增设下稳定板后主梁上表面旋涡结构几乎保持不变,下表面旋涡结构在沿主梁下表面发展壮大的过程中被打碎为较小的旋涡,最后进入尾涡区,且下表面负压值明显减小。虽然模型弹性悬挂时存在明显的流固耦合作用,断面绕流特性会有一些差异,但可以看出下稳定板能较好的控制主梁下表面旋涡结构的发展,有效抑制了涡振的幅值,但被打碎后的旋涡结构不均匀的分布在主梁下表面的凹槽里,容易激发模型的扭转涡激振动。-3°和3°攻角增设下稳定板后主梁断面周围绕流形态与0°风攻角类似,其抑振机理均为下稳定板对主梁下表面旋涡结构发展的抑制作用,但负攻角时下稳定板对下表面旋涡发展的抑制作用有限,其减振效果略差。

(a) -3°攻角

(b) 0°攻角

(c) 3°攻角
5 结 论
对某拟建山区大跨度超高斜拉桥主梁节段模型进行了风洞试验,试验结果表明,π型主梁断面本身具有气动不稳定性,无抗风措施时较易出现明显的涡激振动现象。增设隔流板和下稳定板能在不同程度上优化主梁气动特性,降低主梁涡激共振幅值。最后结合数值模拟,对涡振发生及减振措施的抑振机理进行了初步探讨。结论如下:
(1) 增设一定宽度的隔流板虽然能在一定程度上抑制主梁涡激振动,但其减幅效果有限;设置隔流板后主梁涡振起振风速降低,但锁定风速区间大小保持不变。
(2) 增设两道一定长度的下稳定板对竖弯涡振有明显的抑制作用,一定长度范围内随下稳定板长度的增大减振效果愈加显著,但较长的下稳定板会激发扭转涡振或放大扭转涡振振幅;设置下稳定板后主梁涡振起振风速降低,锁定风速区间有减小的趋势。
(3) 下稳定板的减振效果对风攻角较为敏感,正攻角时的减振效果优于负攻角,且随攻角的增大涡振起振风速逐渐增大。
[1] 华文龙. 边主梁断面叠合梁斜拉桥涡振特性及减振措施研究[D]. 长沙:湖南大学, 2013.
[2] FREIRE A M S, NEGRAO J H O, LOPES A V. Geometrical nonlinearities on the static analysis of highly flexible steel cable-stayed bridges[J]. Computers & Structures, 2006, 84 (31/32):2128-2140.
[3] 许福友, 丁威, 姜峰,等. 大跨度桥梁涡激振动研究进展与展望[J]. 振动与冲击, 2010, 29(10):40-49.
XU Fuyou, DING Wei, JIANG Feng, et al. Development and prospect of study on vortex-induced vibration of long-span bridges[J]. Journal of Vibration & Shock, 2010, 29(10):40-49.
[4] 欧阳克俭, 陈政清, 韩艳,等. 桥面中央开口悬索桥涡激共振与制涡试验研究[J]. 振动与冲击, 2009, 28(7):199-202.
OUYANG Kejian, CHEN Zhengqing, HAN Yan, et al. Vortex-induced vibration of a suspension bridge with central-slotted box section and its control test study[J]. Journal of Vibration and Shock, 2009, 28(7):199-202.
[5] KUBO Y, SADASHIMA K, YAMAGUCHI E, et al. Improvement of aeroelastic instability of shallow π section[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2001, 98(14/15):1445-1457.
[6] 郭增伟, 赵林, 葛耀君,等. 基于桥梁断面压力分布统计特性的抑流板抑制涡振机理研究[J]. 振动与冲击, 2012, 31(7):89-94.
GUO Zengwei, ZHAO Lin, GE Yaojun, et al. Mechanism analysis for vortex-induced vibration reduction of a flat streamlined steel box-shaped girder with airflow-suppressing board based on statistical property of surface pressure[J]. Journal of Vibration and Shock, 2012, 31(7):89-94.
[7] 钱国伟,曹丰产,葛耀君. Ⅱ型叠合梁斜拉桥涡振性能及气动控制措施研究[J]. 振动与冲击, 2015, 34(2):176-181.
QIAN Guowei, CAO Fengchan, GE Yaojun. Vortex-induced vibration performance of a cable-stayed bridge with II shaped composite deck and its aerodynamic control measures[J]. Journal of Vibration and Shock, 2015, 34(2):176-181.
[8] 陈政清. 桥梁风工程[M]. 北京: 人民交通出版社, 2005.
[9] KUBO Y, KIMURA K, SADASHIMA K, et al. Aerodynamic performance of improved shallow π shape bridge deck[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2002, 90(12/13/14/15):2113-2125.
[10] IRWIN P A. Bluff body aerodynamics in wind engineering[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2008, 96(6/7):701-712.
[11] 张志田,卿前志,肖玮,等. 开口截面斜拉桥涡激共振风洞试验及减振措施研究[J]. 湖南大学学报(自然科学版), 2011, 38(7):1-5.
ZHANG Zhitian, QING Qianzhi, XIAO Wei, et al. Vortex-induced vibration and control method for a cable-stayed bridge with open cross section[J]. Journal of Hunan University(Natural Sciences), 2011, 38(7):1-5.
[12] 颜宇光,杨詠昕,周锐. 开口断面主梁斜拉桥的涡激共振控制试验研究[J]. 中国科技论文, 2015, 10(7):760-764.
YAN Yuguang, YANG Yongxin, ZHOU Rui. Experimental study on vortex-induced vibration control measure for cable-stayed bridge with open sections[J]. China Sciencepaper, 2015, 10(7):760-764.
[13] 杨光辉,屈东洋,牛晋涛,等. π型截面涡激振动风洞试验及气动抑制措施研究[J]. 石家庄铁道大学学报(自然科学版), 2015, 38(1):34-39.
YANG Guanghui, QU Dongyang, NIU Jintao, et al. Researches on π-section vortex-induced vibration wind tunnel testing and aerodynamic suppression measures[J]. Jounal of Shijiazhuang Tiedao University (Natural Science), 2015, 38(1):34-39.
[14] 公路桥梁抗风设计规范:JTG/T D60-01—2004[S]. 北京:人民交通出版社, 2004.
[15] 朱乐东. 桥梁涡激共振试验节段模型质量系统模拟与振幅修正方法[J]. 工程力学, 2005, 22(5):204-208.
ZHU Ledong. Mass simulation and amplitude conversion of bridge section model test for vortex-induced oscillation[J]. Engineering Mechanics, 2005, 22(5):204-208.
[16] LEE S, LEE J S, KIM J D. Prediction of vortex-induced wind loading on long-span bridges[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1997(4):267-278.
[17] FUJIWARA A, KATAOKA H, ITO M. Numerical simulation of flow field around an oscillating bridge using finite difference method[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1993(1):567-575.
[18] SHIMADA K, ISHIHARA T. Application of a modifiedk-εmodel to the prediction aerodynamic characteristics of rectangular cross-section cylinders[J]. Journal of Fluids & Structures, 2002, 16(4):465-485.

