滚动轴承内外圈损伤对双盘转子响应特性影响分析
黄亚明, 曹树谦
(1. 天津大学 力学系,天津 300354; 2. 天津市非线性动力学与控制重点实验室, 天津 300354;3. 力学国家级实验教学示范中心(天津大学), 天津 300354)
滚动轴承是航空发动机转子支承系统的重要组成部分,它的运行状态是否正常直接影响到发动机的使用寿命与可靠性。航空发动机滚动轴承故障会导致发动机振动过大、转静子碰摩,甚至造成严重破坏事故。我国某型号战斗机出现过因主轴承服役期内抱死故障导致的航空发动机空中停车、机毁人亡的恶性事故[1]。因此,正确认识滚动轴承故障对转子系统响应的影响,对航空发动机安全运行、延长航空发动机使用寿命具有重要的工程意义。
转子-轴承系统运行稳定性问题一直是转子动力学研究中的重要课题,滚动轴承在运转过程中,承载的滚动体个数及位置发生周期性变化,引起轴承的支撑刚度周期变化,这种参激振动会对转子的动力学行为产生较大的影响。Sunnersjö等[2]考虑了转子惯性力和阻尼力,研究了滚动轴承的变刚度效应,并进行了试验验证;Tiwari等[3]建立了考虑轴承间隙的滚动轴承-转子系统动力学模型,用数值积分的方法研究了轴承间隙对其非线性动力学响应的影响并用Floquet理论分析了其运动稳定性;Sinou[4]建立了考虑轴承间隙、非线性赫兹接触力和不平衡力作用的轴承-转子系统有限元模型,研究了不平衡力对系统稳定性的影响;陈果[5]建立了滚动轴承支承下转子系统的不平衡-碰摩耦合故障动力学模型,分析了转子转速、滚动轴承间隙、碰摩刚度、转子偏心量对系统动力响应的影响;陈予恕等[6]对转子-滚动轴承系统动力学的研究、进展进行了综述。在轴承故障的研究方面,Mc-Fadden等[7]用一系列脉冲序列模拟轴承故障产生的振动冲击;张亚洲等[8]对Mc-Fadden的模型进行了进一步改进,引入了滚动体的随机滑动和周期性变化的振动传递函数,并综合考虑了静态载荷分布和故障点的位置,建立了滚动轴承局部故障的振动数学模型;Brie[9]将滚动轴承简化为一线性时变的质量-刚度-阻尼系统,该模型可以很好地解释轴承元件故障时的振动规律;梁瑜等[10]将滚动轴承的每个滚子与内圈和外圈之间、外圈与轴承座之间、内圈与轴之间的关系分别视为弹簧-质量-阻尼系统,建立起滚动轴承非线性动力学故障模型;陈果等[11-13]在考虑轴承间隙、滚珠与滚道的非线性赫兹接触力以及由滚动轴承支撑刚度变化而产生的变柔性(Varying Compliance,VC)振动的基础上,建立了耦合系统中滚动轴承外圈、内圈及滚动体的损伤动力学模型;王强等[14]针对轴承内圈破损故障,建立起轴承三自由度分段非光滑的故障模型,研究了内圈故障滚动轴承系统周期运动的倍化分岔现象和混沌行为。以上的研究为轴承故障的仿真分析提供了动力学模型基础,但针对轴承故障对系统稳定性影响的研究工作还不太深入,比如并未考虑含轴承故障转子振动随转速、故障程度的变化情况。
本文利用Lagrange方程建立不对称双盘转子-滚动轴承系统的运动微分方程,模型中充分考虑了滚动轴承总体刚度的周期变化以及轴承间隙,在此基础上,建立起了滚动轴承外圈、内圈局域损伤的轴承力模型。然后通过数值模拟研究了系统在不同转速下的运动特性,分别分析了轴承外圈与内圈不同损伤程度对系统动力学响应的影响。本研究工作对转子轴承系统的故障诊断具有一定的参考价值。
1 含滚动轴承故障的双盘转子-滚动轴承系统动力学模型
1.1 双盘转子运动微分方程
对于一个滚动轴承-双盘转子系统,如图1所示。模型中A、D处为相同的滚动轴承支承,B、C为转子的两个转盘,AB=BC=CD=l。假设转盘为刚性,不考虑其变形影响;忽略转子的扭转和轴向振动;轴承轴颈处看作集中质量;转轴为无质量的弹性轴。
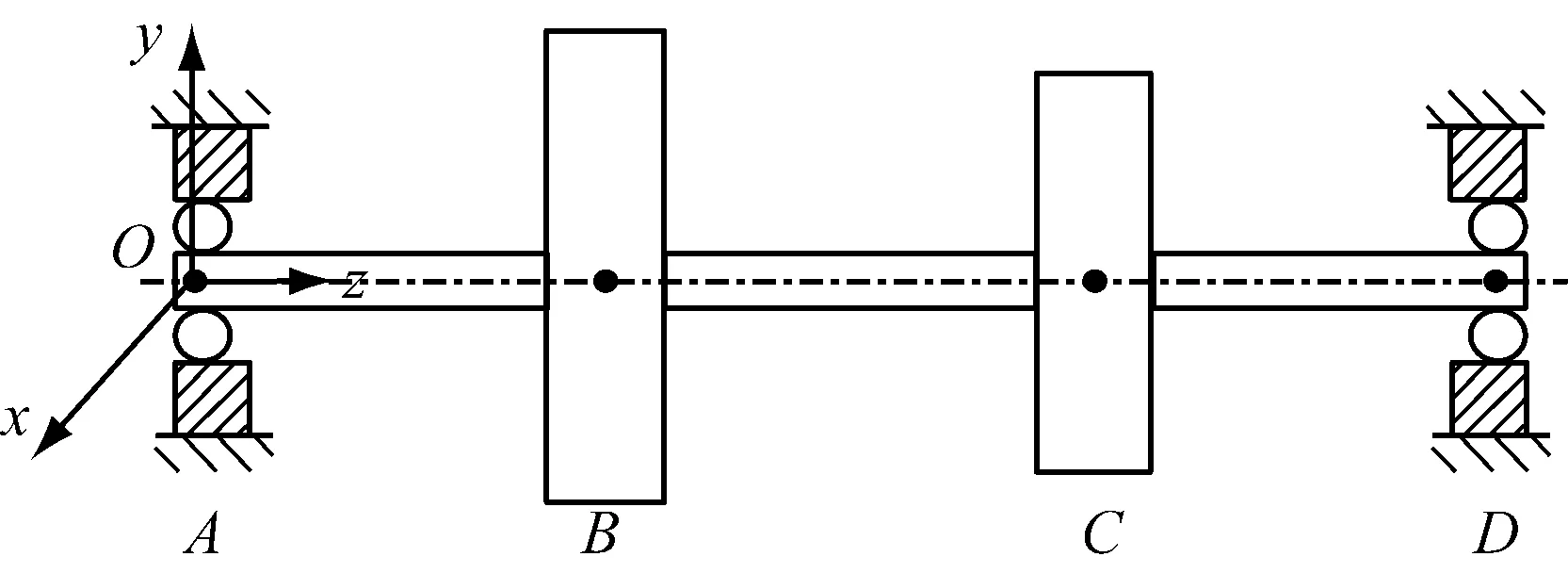
图1 双盘转子-滚动轴承系统动力学模型
每个转盘有4个自由度,其广义坐标为
qdi=[xdi;ydi;θxi;θyi]
(1)
式中:i=1,2。转子盘的动能Tdi可由平动动能Tti和转动动能Tri组成
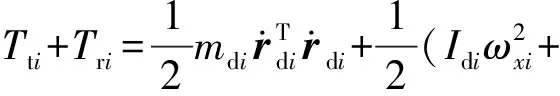
(2)
式中:mdi为转盘的质量;Idi,Ipi分别为转盘的直径和极转动惯量;rdi为转盘中心的位移向量,rdi=(xdi,ydi);ωxi,ωyi,ωzi分别为转盘关于各自坐标系的角速度。
对于轴承轴颈处的集中质量,仅考虑其x和y方向的位移自由度,其广义坐标为qbi=[xbi;ybi]。则每个轴颈的动能为
(3)
系统的耗散能量可由瑞利耗能函数表示
(4)
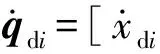
图2为转子在yOz(铅垂面)和xOz(水平面)平面上的投影,则圆盘B、C的相对位移为[15]



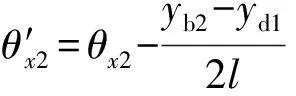
(5)
弹性轴的势能为
(6)
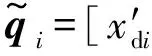
对于非保守系统,Lagrange方程为[16]
(7)

(a) 转子系统在yOz平面的投影

(b) 转子系统在xOz平面的投影
式中:L=T-V为系统的Lagrange函数;qλ为第λ个广义坐标,λ=1,2,…,12;Qλ为对应第λ个自由度上的广义力。
将系统动能、势能、耗散功代入式(7),整理得到双盘转子系统的动力学方程
(8)
式中:Q=[qb1;qd1;qd2;qb2]
Fu(t)=
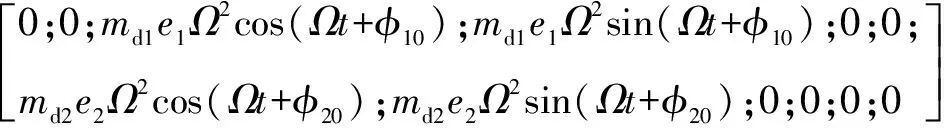
Fb(t)=[Fblx;Fbly;0;0;0;0;0;0;0;0;Fbrx;Fbry];
Fg(t)=[0;ms,1g;0;md,1g;0;0;0;md,2g;0;0;0;ms,2g]。
式中:q为系统广义位移矢量;M,C,G,K分别为系统的惯量矩阵、阻尼矩阵、陀螺矩阵以及刚度矩阵;Fu(t)为不平衡力矢量;Ω为转子转速;e1,e2分别为两圆盘的偏心距;Fb(t)为轴承力矢量;Fg(t)为系统的重力矢量。


(9)
fu(τ)、fb(τ)、fu(τ)分别为无量纲变换后的不平衡力矢量、轴承力矢量、重力矢量。
1.2 健康轴承的轴承力模型[17-19]
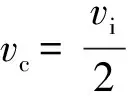
(j-1),j=1,2,…,Nb
(10)

图3 滚动轴承模型
设内圈中心在水平与铅直方向的振动位移分别为x,y,初始轴承间隙为δ0,则第j个滚子与滚道之间的法向接触变形量为
δj=xcosθj+ysinθj-δ0
(11)
由非线性赫兹理论可知,只有δj> 0才有作用力,则
δj)
(12)
式中:Cb为赫兹接触刚度;H(·)为亥维赛函数;Fj在x,y方向上的分量为
Fjx=Fjcosθj
Fjy=Fjsinθj
(13)
所以,滚动轴承产生的轴承力为
δj)cosθj
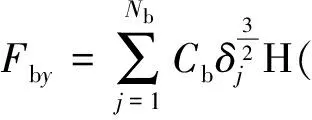
(14)
1.3 外圈损伤时轴承力模型
设滚动轴承外圈有局部剥落故障,如图4所示。故障的角位置为α,剥落的宽度为β,剥落的厚度为h。
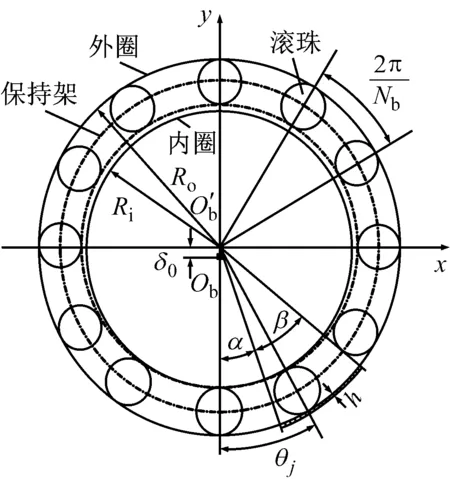
图4 滚动轴承外圈损伤示意图
为了模拟轴承外圈的损伤故障,认为滚珠进入损伤区域后,轴承间隙突然加大导致滚珠与轴承内外滚道接触面间的赫兹接触力突然降低或变为零。此时,滚珠与滚道间的法向接触变形量为
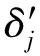
(15)
根据非线性赫兹接触理论,可以得到该滚珠与滚道所产生的接触压力为

H(xcosθj+ysinθj-δ0-h)
(16)
所以,滚珠在滚道上运动一周,两者间的接触压力是一个分段函数
(17)
1.4 内圈损伤时轴承力模型
设滚动轴承内圈有局部剥落故障,如图5所示。故障的角位置为α,剥落的宽度为β,剥落的厚度为h。
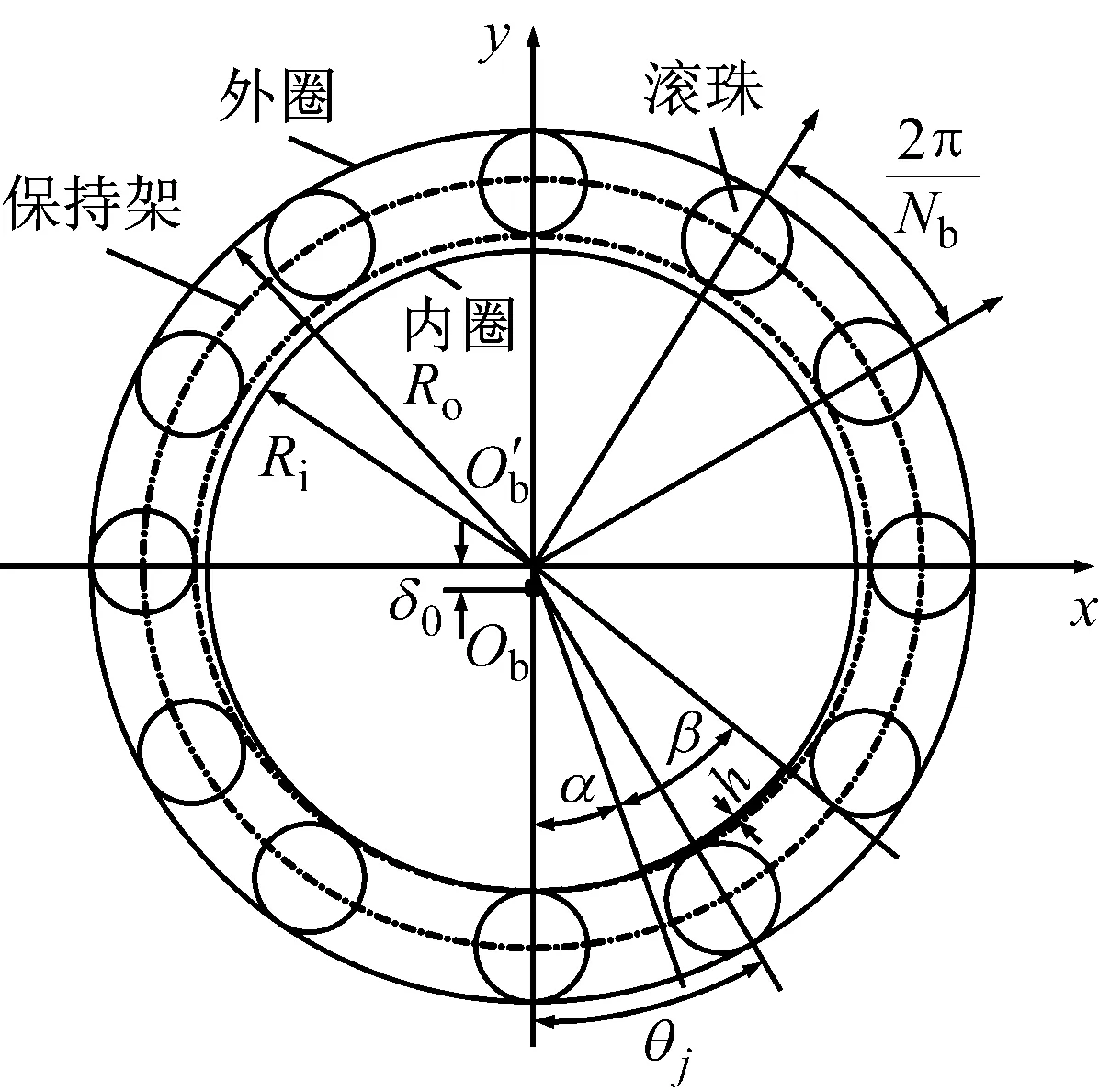
图5 滚动轴承内圈故障示意图
与外圈故障相同,滚珠在滚道上运动一周,两者间的接触压力也是一个分段函数,区别在于,内圈固定在转轴上随转子一起转动,因此,缺陷位置也一直在变化。当滚珠经过缺陷位置时,有
α+Ωt+2kπ<θj≤α+Ωt+β+2kπ
(18)
所以滚珠运动一周,与滚道间的接触压力为
(19)
2 转子-滚动轴承系统的动力学特性
2.1 初始系统参数
选择转子系统的基本参数为:转盘B的质量为15 kg,直径转动惯量为0.037 5 kg·m2,极转动惯量为0.075 kg·m2,偏心距为0.01 mm;转盘C的质量为12 kg,直径转动惯量为0.019 2 kg·m2,极转动惯量为0.038 4 kg·m2,偏心距为0.005 mm;两端轴承处的集中质量均为1.00 kg,转轴材料的杨氏模量为2×1011Pa,直径为20 mm;两端轴承处的阻尼为1 050 N/(m·s-1),两转盘处的阻尼为2 100 N/(m·s-1)。滚动轴承型号为6204号深沟球轴承,其主要尺寸及计算参数为:内滚道半径Ri=12.348 mm,外滚道半径Ro=21.116 mm,节圆直径D=33.5 mm,滚珠直径db=8.731 mm,滚珠个数Nb=7,接触刚度Cb=5×109N/m3/2,初始轴承间隙δ0=5 μm。本文采用经典的四阶龙格库塔法对系统进行数值求解。
2.2 轴承正常时的系统动力学响应
为了研究不同轴承故障对转子轴承系统动力学响应特性的影响,分别对系统在没有故障、右端轴承外圈出现故障、右端轴承内圈出现故障的三种情况下的运动进行数值模拟。

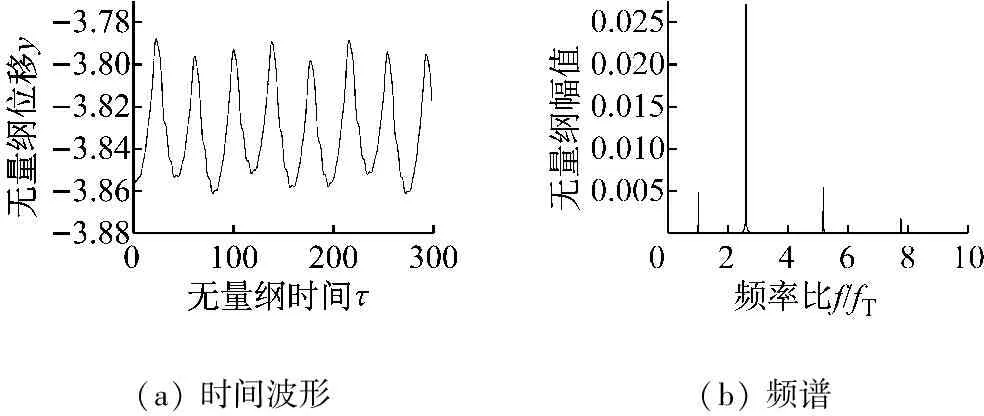
(a)时间波形(b)频谱
图6 转速比p=0.055时响应的波形图及频谱图
Fig.6 Time-domain waveform and frequency spectrum at speed ratio of 0.055
随着转速的升高,不平衡旋转激励的影响逐渐显现出来,并逐渐取代VC参数激励成为影响系统振动特性的主要因素。图7(a)、图7(b)分别为系统运动的分岔图与三维瀑布图,从图7可知,当p<0.769时,频谱中的频率成分有1倍频、2倍频、VC频率以及(VC-1)倍频成分,随转速的加大,不平衡旋转激励频率成分逐渐增大,而VC频率以及其谐波成分逐渐消失,系统从拟周期运动逐渐进入单周期运动;转速比p为1.619~2.011,系统出现2倍周期运动状态,从瀑布图中可以看出占比较强的1/2倍频,图8(a)、图8(b)分为p=1.813时系统响应的轴心轨迹图与庞加莱截面图,轴心轨迹图上显示出两个环,庞加莱图中出现了两个孤立的点,说明系统呈明显的2倍周期运动状态;在转速比p=2.011时,系统经倒分岔又回到单周期运动状态。
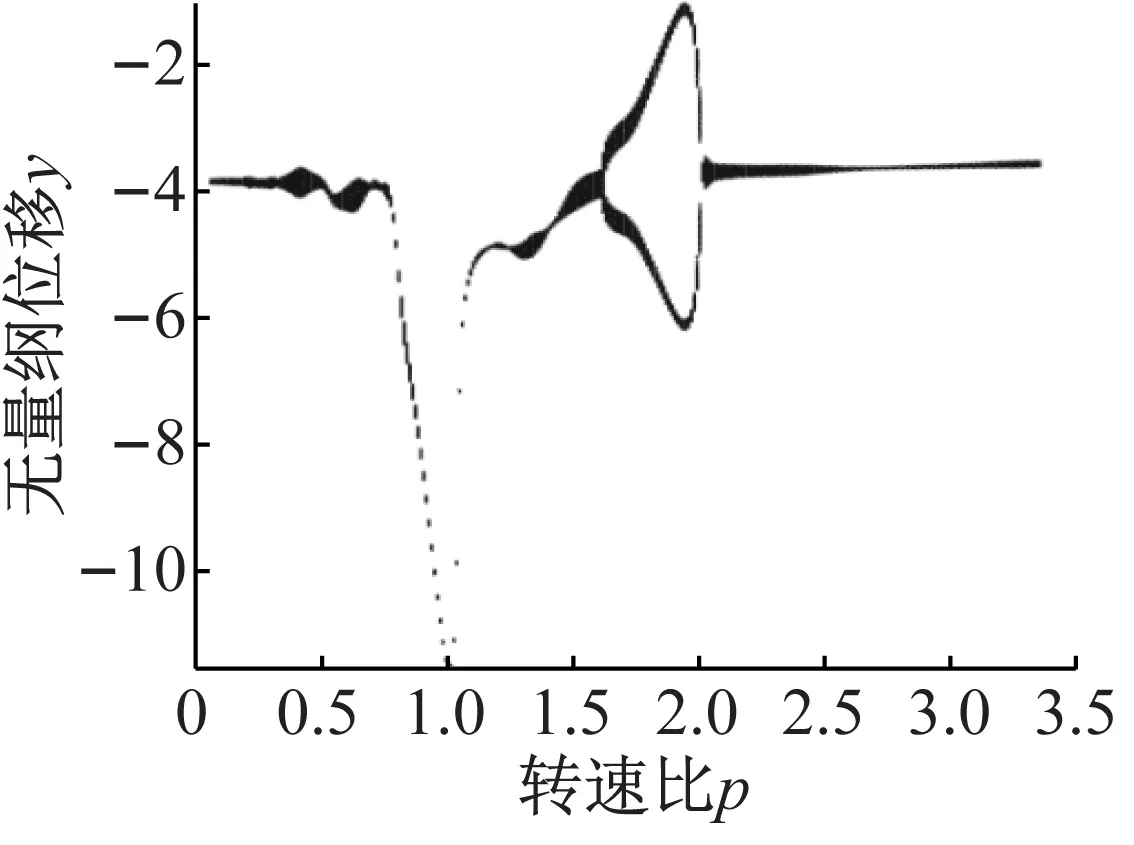
(a) 分岔图

(b) 瀑布图
2.3 含轴承滚道局域损伤时的系统动力学响应
当滚动轴承发生故障时,系统不仅受到不平衡的旋转频率激励和来自轴承内部的VC参数激励,还有来自于轴承故障的附加激励力。不同的损伤程度下系统的运动特性可能有不同的表现,因此分别研究含轴承外圈故障转子与含内圈故障转子在不同损伤尺寸时的动力学表现。表1为6204号滚动轴承各故障特征频率。

(a)轴心轨迹图(b)庞加莱截面图
图8 转速比p=1.813时系统运动轴心轨迹图与庞加莱截面图
Fig.8 Orbit plot and Poincaré map at speed ratio of 1.813

表1 深沟球轴承6204的故障特征频率
2.3.1 外滚道损伤
当存在轴承外滚道故障时,设损伤宽度β=0.2π,损伤深度h=0.10 mm,转轴转速比p=0.165。图9为含故障转子B盘y方向运动的位移时域波形与频谱图。从图9(a)可知,转子振动位移的周期冲击响应,说明由于轴承外圈故障引起的冲击振动传递到了转子B处;从图9(b)可知,轴承外圈故障特征频率2.58fr的存在,另外图中5.17fr、7.76fr、10.35fr等与轴承外圈故障特征频率一起构成了一簇间隔正好为特征频率边频带。轴承故障引起的共振峰位于5.17fr处,以5.17fr为中心,边频带幅值随频率增大而逐渐衰减。对比文献[22]中的结果,本文中滚动轴承外滚道损伤的建模是有效的。

(a)时间波形(b)频谱图
图9 含轴承外圈故障转子转速比p=0.165时响应的波形图及频谱图
Fig.9 Time-domain waveform and Frequency spectrum of the system with a damage in outer ring at speed ratio of 0.165
为得到轴承外滚道不同损伤宽度时对转子系统动力学特性的影响,对损伤宽度分别为0.1π、0.2π、0.3π、0.4π,损伤深度均为0.10 mm时转子的运动过程进行数值模拟,得到四种故障程度下系统运动的分岔图、幅频特性曲线、庞加莱图等。通过分析可以发现,外滚道损伤宽度的变化会对转子系统的运动产生较大的影响。
图10为轴承外滚道不同损伤宽度情况下的转子系统运动分岔图。由图10可知,与正常系统相比,含外圈故障转子系统的多频响应运动的速度区间明显增大,这说明轴承外滚道的损伤对转子系统的稳定性产生了影响,且损伤宽度越大,不稳定区间越大。图11为四种损伤程度下p=0.550时转子的频谱图,通过对比可知,随着损伤宽度的增加,外圈故障频率的幅值也在逐渐增大,分频成分也越来越多。

(a)β=0.1π(b)β=0.2π

(c)β=0.3π(d)β=0.4π
图10 外滚道损伤宽度不同时转子运动分岔图
Fig.10 Bifurcation diagrams of the system with different width of the damage in the outer ring
随着转速升高,当β=0.1π、0.2π、0.3π时,转子系统都经历了2倍周期的运动状态,β=0.1π时系统出现2倍周期运动的转速比区间为1.621~1.994,β=0.2π时系统出现2倍周期运动的转速区间为1.626~1.948,β=0.3π时转速为1.637~1.877,由此可见,随着轴承外滚道损伤宽度的增大,系统2倍周期运动的转速区间逐渐缩小,当损伤宽度达到0.4π时,系统2倍周期运动状态不复存在。图12是转速比p=1.813时轴承外滚道在不同损伤宽度下系统运动庞加莱图。从图12可知,在同一转速下,四种情况下的庞加莱图形状都不相同,损伤宽度为0.1π、0.2π、0.3π时系统做2倍周期运动,而损伤宽度为0.4π时,系统做拟周期运动。这些现象说明轴承外滚道的损伤产生的附加激励力对轴承游隙的非线性影响产生干扰,随着损伤宽度的增加,附加激励力甚至会压制游隙的非线性因素。
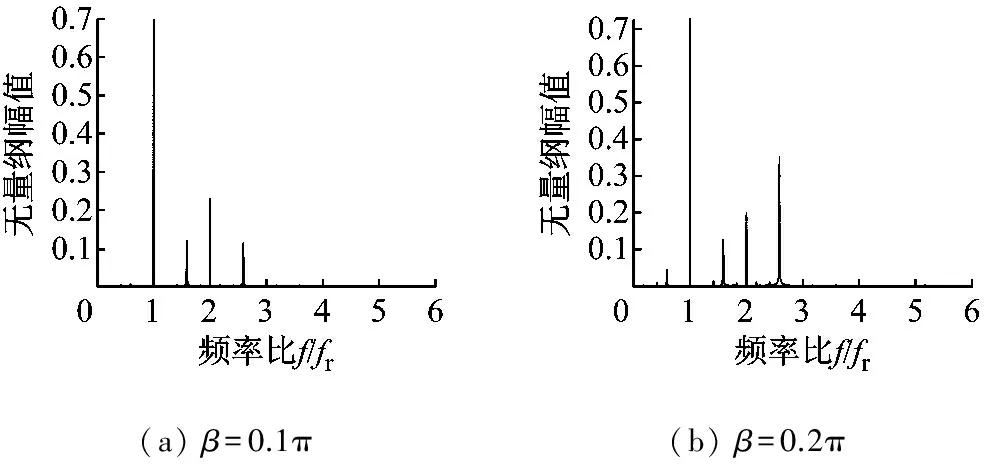
(a)β=0.1π(b)β=0.2π
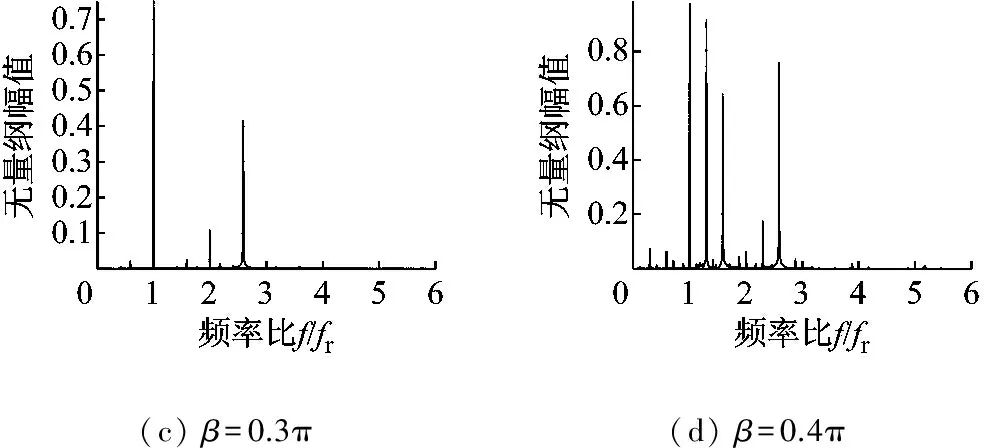
(c)β=0.3π(d)β=0.4π
图11p=0.550时不同损伤宽度下的转子运动频谱图
Fig.11 Frequency spectrum of the system with different width of the damage in the outer ring at speed ratio of 0.550
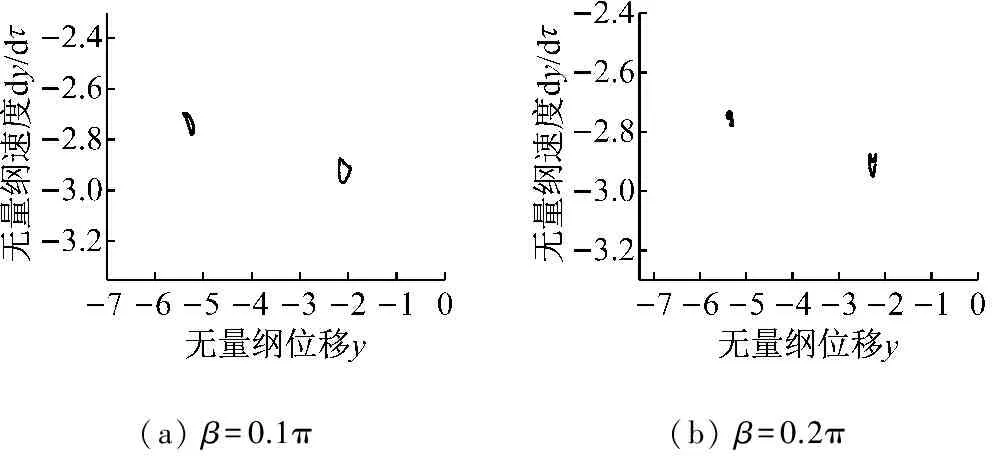
(a)β=0.1π(b)β=0.2π

(c)β=0.3π(d)β=0.4π
图12 外滚道不同损伤宽度下p=1.813时的庞加莱图
Fig.12 Poincaré maps of the system with different width of the damage in the outer ring at speed ratio of 1.813
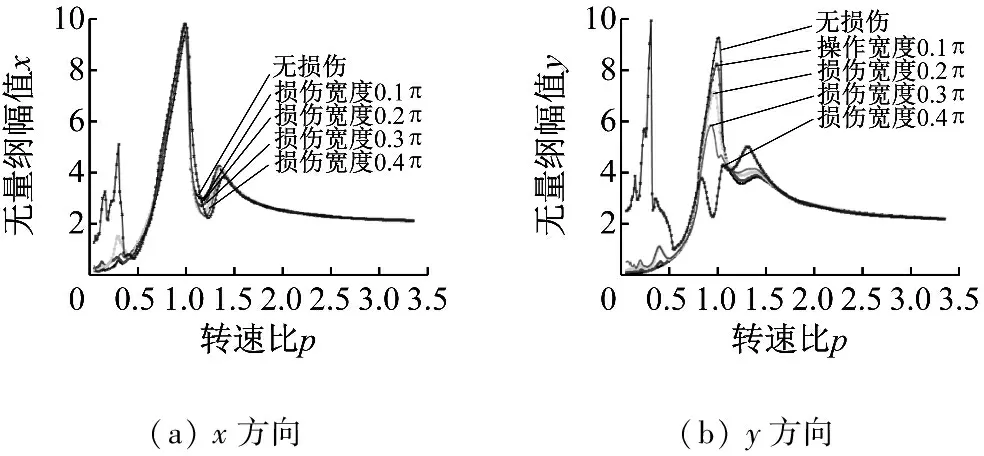
损伤宽度也影响着系统振动幅值。如图13是转子B盘处x,y两方向振动位移的幅频特性曲线。从图中可以看出,轴承损伤宽度对两个方向振动系统振动幅值的影响不完全一致。在转速较低时,损伤宽度越大,x,y方向振动的幅值也越大;随着转速升高,在0.550~1.099转速比区间以及p>1.465转速区间内,损伤宽度对x方向振幅的影响不大。在1.099~1.465区间内,随着损伤宽度的增大,系统x方向振幅逐渐减小。而在y方向,在0.802~1.099转速区间内,振幅逐渐减小,在1.099~1.538转速比区间内正好相反,当p>1.538后,损伤宽度的影响不明显。
(a)x方向(b)y方向
图13 外滚道损伤宽度不同时转子振动幅频特性曲线
Fig.13 Frequency-response of the system with different width of the damage in the outer ring
外滚道损伤深度的变化对转子运动特性的影响并不明显,如图14所示。当损伤宽度β=0.2π,损伤深度分别为0.05 mm、0.10 mm、0.15 mm、0.20 mm时B盘x,y方向位移响应的幅频曲线完全重合。这是因为损伤的深度远大于轴承游隙,滚珠通过损伤区域时,没有产生挤压变形,接触力突变为零,所以损伤的深度变化不会对轴承的受力情况产生影响。

(a)x方向(b)y方向
图14 外滚道损伤深度不同时转子振动幅频特性曲线
Fig.14 Frequency-response of the system with different depth of the damage in the outer ring
2.3.2 内滚道损伤
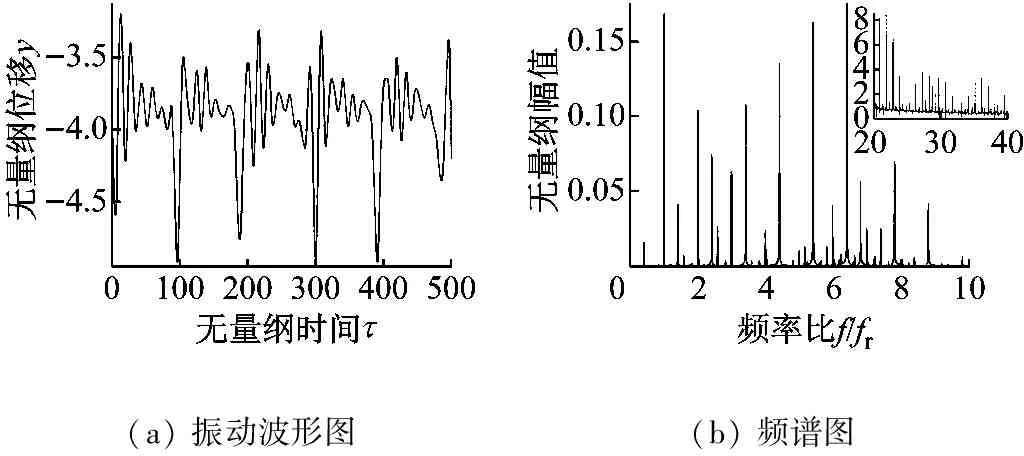
当存在轴承内滚道故障时,设损伤尺寸仍为β=0.2π,h=0.10 mm,图15为含轴承内圈故障转子在转速比p=0.165时的振动波形及频谱图。图15(a)中同样出现了周期冲击响应。由于内圈的转动,冲击响应振幅受到旋转频率的调制,产生了类似拍振的现象。图15(b)中fr、2fr、3fr、4fr、5fr、6fr与2.413fr、3.413fr、4.413fr、5.413fr、6.413fr、7.413fr分别组成了两簇边频带间隔为旋转频率fr的边频带簇,高频部分也出现了多组边频带簇,两个边频带簇的间隔正好为内圈故障的特征频率4.413fr。该结论与文献[22]中的结果一致,说明本文对轴承内圈故障的建模的准确性。
为研究轴承内滚道损伤对转子运动特性的影响,对内滚道损伤宽度分别为0.1π、0.2π、0.3π、0.4π,损伤深度均为0.10 mm时转子的运动过程进行数值计算,得到四种情况下的系统运动分岔图、幅频特性曲线、庞加莱图等。通过分析可知,内滚道损伤宽度的变化也会影响转子的运动情况。
(a)振动波形图(b)频谱图
图15 含轴承内圈故障转子转速比p=0.165时响应的波形图及频谱图
Fig.15 Time-domain waveform and Frequency spectrum of the system with a damage in the inner ring at speed ratio of 0.165
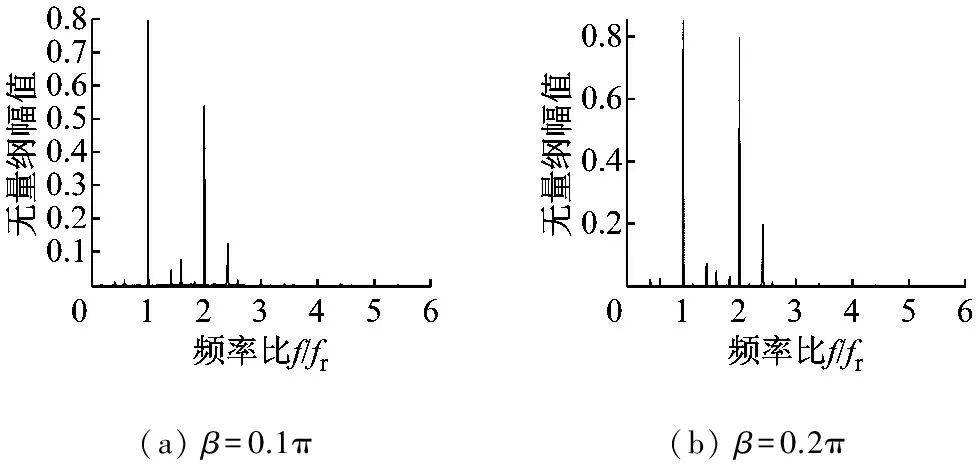
图16为转子在轴承内滚道不同损伤宽度时的运动分岔图。图17(a)~图17(d)为四种损伤情况下转速比为p=0.550时系统响应的频谱图,从图17可知,四种情况下的系统运动均表现为旋转频率和内圈故障频率通过和与差的不同组合,以及旋转频率与VC频率的组合。其中,旋转频率与其2倍频占绝大优势;随着内滚道损伤宽度的增大,在1倍频与2倍频幅值逐渐增大的同时,二者的比值逐渐减小。
(a)β=0.1π(b)β=0.2π

(c)β=0.3π(d)β=0.4π
图16 内滚道损伤宽度不同时转子运动分岔图
Fig.16 Bifurcation diagrams of the system with different width of the damage in the inner ring
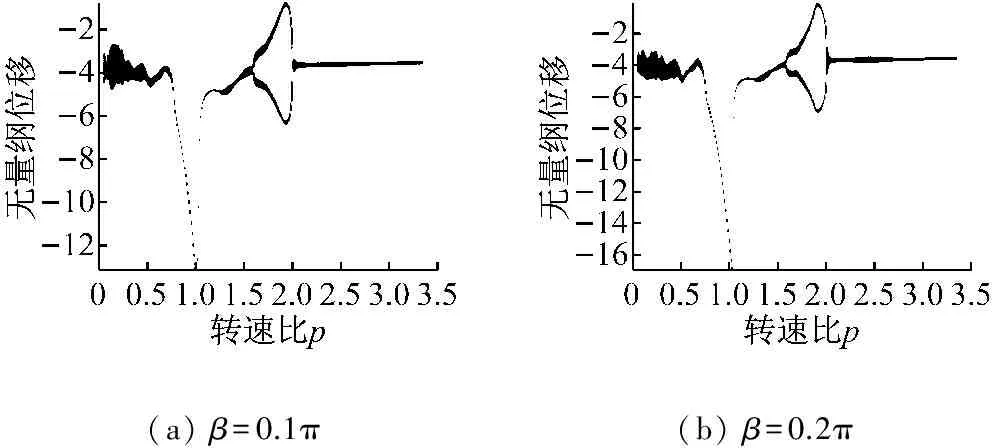
四种情况下系统都经历了2倍周期运动状态,当β=0.1π时,系统2倍周期运动的转速区间为1.599~2.027,当β=0.2π时,系统2倍周期运动的转速区间为1.588~2.033;当β=0.3π时,系统2倍周期运动的转速区间为1.575~2.044;当β=0.4π时,系统2倍周期运动的转速区间为1.550~2.036。可见,随着损伤宽度的增加,系统出现2倍周期运动的转速逐渐提前,转速区间跨度也逐渐增大。图18 是转速比p=1.813时轴承内滚道在不同损伤宽度下系统运动庞加莱图。从图中可以看出,在同一转速下,随着损伤宽度的增加,系统运动的庞加莱图由两个封闭的环逐渐缩小为两个独立的点。这些现象说明轴承内滚道损伤产生的附加激励力同样会对轴承游隙的非线性因素产生影响;与外滚道损伤不同的是,随着损伤宽度的增加,附加激励力会逐渐增强轴承游隙的非线性因素。
(a)β=0.1π(b)β=0.2π
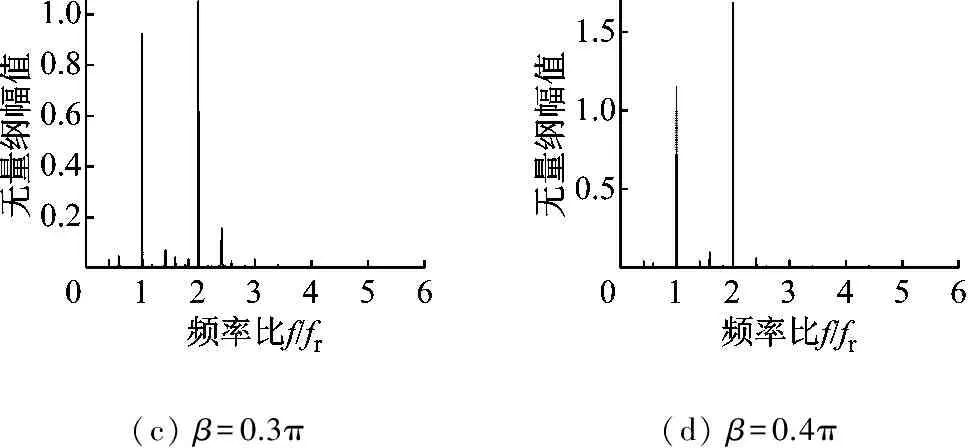
(c)β=0.3π(d)β=0.4π
图17 转速比p=0.550时内滚道不同损伤宽度下的转子运动
Fig.17 Frequency spectrum of the system with different width of the damage in the inner ring at speed ratio of 0.550
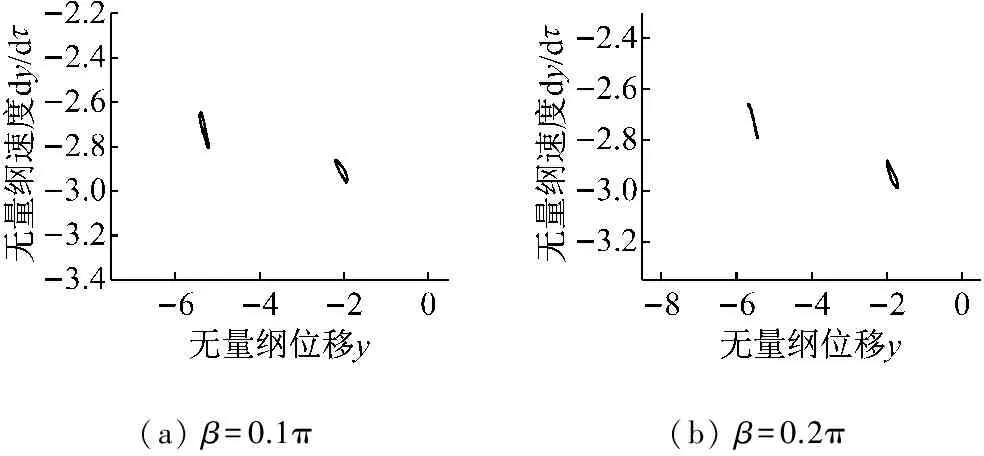
(a)β=0.1π(b)β=0.2π

(c)β=0.3π(d)β=0.4π
图18 内滚道不同损伤宽度下p=1.813时的庞加莱图
Fig.18 Poincaré maps of the system with different width of the damage in the inner ring at speed ratio of 1.813
滚动轴承内圈损伤宽度对系统振动幅值的影响,如图19所示。从图19可知,当p<1.077时,随着内滚道损伤宽度的增加,系统x,y方向的振幅也在增大,x方向的最大振幅由无故障时的8.722增大到0.4π时的31.08,增幅达到256%;y方向由无故障时的9.267增大到0.4π时的31.03,增幅达到235%。当p>1.077时,x方向上的振幅受损伤宽度的影响不明显;而在y方向,当转速比p在1.867~2.011区间内时,系统振幅也受到损伤宽度的影响,损伤宽度越大,振幅越大。
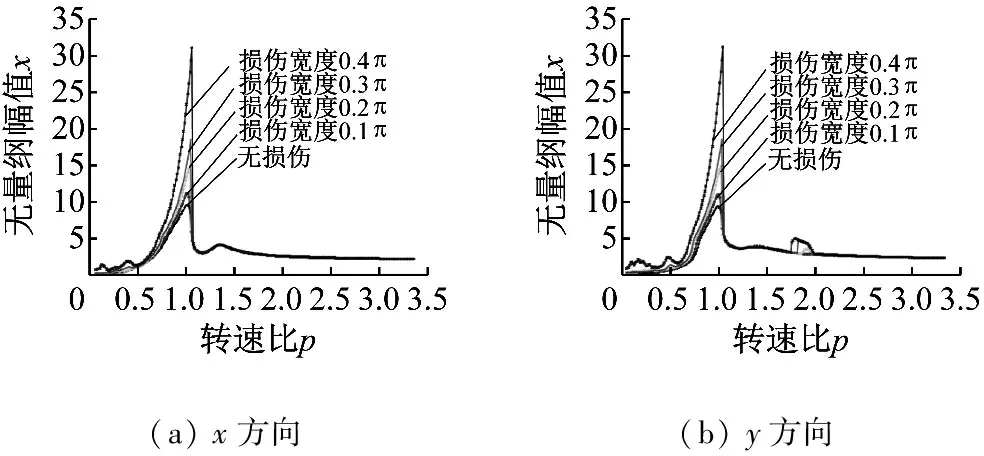
(a)x方向(b)y方向
图19 内滚道损伤宽度不同时转子振动幅频特性曲线
Fig.19 Frequency-response of the system with different width of the damage in the inner ring
与外滚道故障相同,内滚道损伤深度的变化对转子运动特性的影响并不明显,如图20所示。当损伤宽度β=0.2π,损伤深度分别为0.05 mm、0.10 mm、0.15 mm、0.20 mm时B盘x,y方向位移响应的幅频曲线完全重合。

(a)x方向(b)y方向
图20 内滚道损伤深度不同时转子运动振动幅频特性曲线
Fig.20 Frequency-response of the system with different depth of the damage in the inner ring
3 结 论
针对非对称双盘转子-轴承系统,在正常滚动轴承支承刚度周期变化的基础上,建立了轴承外圈、内圈剥落故障时的轴承力模型,考虑了由于轴承局部剥落故障导致的轴承间隙突然增大引起的轴承力突变,研究了系统在不同转速下的运动特性,分别分析了轴承外圈与内圈不同损伤程度对系统动力学响应的影响,结果表明:
(1) 轴承外圈和内圈发生故障时,都会对双盘转子-轴承系统的运动特性产生显著影响,特别是在低转速的时候,故障会激发出多种复杂频率成分,使系统的振动幅值增大。不同的故障类型表现出了各自的故障特征频率,并且内圈故障引起冲击振动幅值受转轴旋转频率的调制,因而转子会产生类似拍振的现象。
(2) 轴承外滚道出现损伤时,当损伤深度一定,随着损伤宽度的增大,系统2倍周期运动区间逐渐减小到消失,外滚道损伤产生的附加激励力会逐渐压制轴承间隙的非线性因素对系统运动的作用。而在转速较低时(p<0.550),系统x,y两方向上的振动幅值都是随损伤宽度的增加而增大;在转速较高时(p>1.465),损伤宽度对系统振幅影响不明显。而在中间转速区间内,两方向的振幅变化情况有所不同;在转速比为1.099~1.465区间内,随着损伤宽度的增大,系统x方向振幅逐渐减小;而在y方向,在0.802~1.099转速比区间内,振幅逐渐减小,在1.099~1.538转速区间内正好相反。
(3) 轴承内滚道出现损伤时,随着损伤宽度的增大,系统开始2倍周期运动的转速逐渐提前,转速区间跨度也逐渐增大,内滚道损伤产生的附加激励力会加强轴承间隙非线性因素的影响。转速比p<1.077时,随着内滚道损伤宽度的增加,系统x,y方向的振幅也在增大;转速p>1.077时,损伤宽度的增大对x方向振幅影响不大,而在y方向,损伤宽度对振幅有一影响区间为1.867~2.011。
(4) 轴承损伤深度的变化不会对转子的运动特性造成影响。由于损伤的深度远大于轴承游隙,滚珠通过损伤区域时,没有产生挤压变形,接触力突变为零,所以损伤的深度变化不会对轴承的受力情况产生影响。
(5) 总体来讲,轴承内外圈损伤故障对双盘转子振动幅值的影响在低速区间以及临界转速附近尤为明显。
[1] 申中杰,陈雪峰,何正嘉,等. 基于相对特征和多变量支持向量机的滚动轴承剩余寿命预测[J]. 机械工程学报, 2013, 49(2):183-189.
SHEN Zhongjie, CHEN Xuefeng, HE Zhengjia, et al. Remaining life predictions of rolling bearing based on relative features and multivariable support vector machine[J]. Journal of Mechanical Engineering, 2013, 49(2):183-189.
[2] SUNNERSJÖ C S. Varying compliance vibrations of rolling bearings[J]. Journal of Sound & Vibration, 1978, 58(3):363-373.
[3] TIWARI M, GUPTA K, PRAKASH O. Effect of radial internal clearance of a ball bearing on the dynamics of a balanced horizontal rotor[J]. Journal of Sound & Vibration, 2000, 238(5):723-756.
[4] SINOU J J. Non-linear dynamics and contacts of an unbalanced flexible rotor supported on ball bearings[J]. Mechanism & Machine Theory, 2009, 44(9):1713-1732.
[5] 陈果. 具有不平衡-碰摩耦合故障的转子-滚动轴承系统非线性动力学研究[J]. 振动与冲击,2008, 27(4):43-48.
CHEN Guo. Nonlinear dynamic study on a rotor-ball bearing system with unbalance-rubbing coupling fault[J]. Journal of Vibration and Shock, 2008, 27(4):43-48.
[6] 陈予恕,张华彪. 航空发动机整机动力学研究进展与展望[J]. 航空学报,2011, 32(8):1371-1391.
CHEN Yushu, ZHANG Huabiao. Review and prospect on the research of dynamics of complete aero-engine systems[J]. Acta Aeronautical et Astronautica Sinica, 2011, 32(8):1371-1391.
[7] MC-FADDEN P, SMITH J. Model for the vibration produced by a single point defect in a rolling element bearing[J]. Journal of Sound & Vibration, 1984, 96(1):69-82.
[8] 张亚洲,石林锁. 滚动轴承局部故障数学模型的建立与应用[J]. 振动与冲击,2010, 29(4):73-76.
ZHANG Yazhou, SHI Linsuo. Establishment and application of mathematical models for roiling element bearings with localized faults[J]. Journal of Vibration and Shock, 2010, 29(4):73-76.
[9] BRIE D. Modelling of the spalled rolling element bearing vibration signal: an overview and some new results[J]. Mechanical Systems & Signal Processing, 2000, 14(3):353-369.
[10] 梁瑜,贾利民,蔡国强,等. 滚动轴承的非线性动力学故障模型研究[J]. 中国铁道科学,2014, 35(1):98-104.
LIANG Yu, JIA Limin, CAI Guoqiang, et al. Research on nonlinear dynamics fault model of rolling bearing[J]. China Railway Science, 2014, 35(1):98-104.
[11] 陈果. 转子-滚动轴承-机匣耦合系统中滚动轴承故障的动力学分析[J]. 振动工程学报,2008, 21(6):577-587.
CHEN Guo. Dynamic analysis of ball bearing faults in rotor-ball bearing-stator coupling system[J]. Journal of Vibration Engineering, 2008, 21(6):577-587.
[12] 张建军,王仲生,芦玉华,等. 基于非线性动力学的滚动轴承故障工程建模与分析[J].振动与冲击,2010, 29(11):30-34.
ZHANG Jianjun, WANG Zhongsheng, LU Yuhua, et al. Nonlinear dynamic modeling for localized defects in a rolling element bearing[J]. Journal of Vibration and Shock, 2010, 29(11):30-34.
[13] 关贞珍,郑海起,王彦刚,等. 滚动轴承局部损伤故障动力学建模及仿真[J]. 振动、测试与诊断,2012, 32(6):950-955.
GUAN Zhenzhen, ZHENG Haiqi, WANG Yangang, et al. Fault dynamic modeling and simulating of rolling bearing with localized defect[J]. Journal of Vibration, Measurement & Diagnosis, 2012, 32(6):950-955.
[14] 王强,刘永葆,徐慧东,等. 内圈故障滚动轴承系统周期运动的倍化分岔[J]. 振动与冲击,2015, 34(23):136-142.
WANG Qiang, LIU Yongbao, XU Huidong, et al. Period-doubling bifurcation of a rolling bearing system with inner race fault[J]. Journal of Vibration and Shock, 2015, 34(23):136-142.
[15] 沈松,郑兆昌,应怀樵. 非对称转子-轴承-基础系统的非线性振动[J]. 振动与冲击,2004, 23(4):31-33.
SHEN Song, ZHENG Zhaochang, YING Huaiqiao. Nonlinear vibration of unsymmetrical rotor-bearing-foundation system[J]. Journal of Vibration and Shock, 2004, 23(4):31-33.
[16] 白雪川. 航空发动机反向旋转双转子系统动力学特性研究[D]. 天津:天津大学,2014.
[17] CHEN G. A new rotor-ball bearing-stator coupling dynamics model for whole aero-engine vibration[J]. Journal of Vibration and Acoustics, 2009, 131(6): 061009(1-5).
[18] 成玫,孟光. 含Alford力的非线性转子-滚动轴承系统动力分析[J]. 中国机械工程,2011, 22(23): 2806-2812.
CHENG Mei, MENG Guang. Dynamic analysis of a rotor-ball bearing nonlinear system with alford force[J]. China Mechanical Engineering, 2011, 22(23): 2806-2812.
[19] 曹树谦,王俊,韩研研,等. 耦合故障转子系统的降维及动力学特性[J]. 天津大学学报(自然科学与工程技术版),2015(4):318-327.
CAO Shuqian, WANG Jun, HAN Yanyan, et al. Dimension reductions and dynamic characteristics of rotor system with coupling faults[J]. Journal of Tianjin University (Science and Technology), 2015(4):318-327.
[20] FUKATA S, GAD E, KONDOU T, et al. On the radial vibration of ball bearings (computer simulation)[J]. Transactions of the Japan Society of Mechanical Engineers C, 1984, 50:1703-1708.
[21] MEVEL B, GUYADER J. Routes to chaos in ball bearings[J]. Journal of Sound & Vibration, 1993, 162(3):471-487.
[22] 梅宏斌.滚动轴承振动监测与诊断[M].北京:机械工业出版社,1996.

