基于动态反向映射图的流图划分方法

李茜锦

（四川大学计算机学院，成都 610065）

0 引言

图经常被用来对应用问题进行抽象建模，把图划分为更小的块是一个基本的算法操作，对于遍历、路径寻找等问题，图划分通常是一个减少复杂性或并行化的重要子问题。随着应用中更大的图的实例的出现，例如科学估算、社会网络或者合作交易网络，图划分变得越来越重要和困难，同时通过在图上执行计算来提取知识变得越来越具有挑战性。

为了找到越来越亟需的快速图划分方法，将流这一概念与图划分相结合的流图划分算法被提出[8]。流图划分追求卓越的划分速度，随之而来还有许多等待解决的问题，包括异构环境、有向图与无向图等，虽然已经出现了异构环境中的流图划分[11]等对流图算法的改进，但对有向图和无向图进行区分的研究仍然欠缺。

在流图划分中，每次只能处理一个元数据，而元数据只包含非常有限的信息：当前顶点和其邻居，或者当前顶点和其某一个邻居。对于无向图来说，这种有限的数据总能获得当前顶点的完整信息，但是对于有向图，在元数据中无法获得当前顶点的所有信息，甚至由于流的限制，在以顶点为中心的划分方法中，划分结果会忽略所有的没有出度的顶点。同时，有向图是无法回避的一个问题，社交网络、交流通讯网络等都存在大量的有向图，所以本文提出了动态反向映射图来解决有向流图划分的问题。

1 相关工作

图划分有长久的研究历史，蕴含很多问题以及或简或繁的解决方法。一般来说，所讨论的图划分都为平衡图划分，平衡图划分是一个NP完全问题[1-2]，其有两个需要达到的目标，第一是尽可能减少被分区切割的边的数量，第二是每个分区有大致相同的大小。显然，如果去掉平衡这一限制，第一个目标会非常容易达到最优。平衡图划分给定一个图G和数字k，把G划分为k个大小相差不多的子图，同时最小化被切割的边的数量。

全局算法根据整个图的信息来计算划分结果，对于大图而言非常不适用，所以启发式方法被提出以解决图划分问题。Kernighan和Lin[3]第一个提出启发式方法——KL算法，而后Fiduccia和Mattheyses[4]提出FM算法将运行时间提升到线性运行时间。Karypis等[5]提出并行多层级图划分算法，在每一个层级上进行最小二分，进一步缩短了划分所需的时间。启发式算法不能保证性能，但是许多启发式的实现，例如MEITIS[6]、Chaco[7]等，在实际中应用中非常的有效。

由于对目前的大规模图而言，离线启发式方法也变得吃力，Stanton和kliot[8]提出一系列不区分无向图和有向图的使用启发式方法的在线流图划分方法，简单提到图数据流中顶点顺序对划分结果的影响。Fennel[9]结合其他启发式方法的流划分框架对该工作进行了扩展。Joel Nishimura和Johan Ugander[10]更进一步提出Restreaming LDG和Restreamig Fennel，使用最近的图划分结果来生成初始图划分，该方法提升了流图划分的结果质量，但却减慢了划分速度。平衡图划分问题存在一种变形，给每个分区添加了不同的大小限制，称为非平衡图划分，或异构环境中的图划分。Ning Xu等[11]提出了一种在异构环境中的流图划分方法,Robert Krauth⁃gamer等[12]提出了非平衡图划分。

2 动态反向映射图

2.1 信息丢失

图1 有向图示例

对于无向图来说可以从一条顶点信息中获得其所有的邻居信息，但是对于有向图，并不能从一条顶点信息中获取其所有的邻居信息，现有的流图划分算法大都忽略了有向图的信息丢失问题。举例来说明，如图1，从顶点1可以得到其与顶点2，8相连，但是对于流式处理方法来说，当处理到顶点2和8时却无法得知其与顶点1相连，故而无法准确判断顶点2和8在各个分区的邻居数量，这会造成边信息的丢失，导致不佳的图划分结果。但若对全图遍历以获取准确的顶点间边的信息又会失去流式处理一次遍历的初衷，增大图划分算法的执行时间。

2.2 动态信息补全

本文提出的动态反向映射图，随着图划分过程的进行，会逐步保存可利用的信息，去除无用信息。动态反向映射图DG=(DV,DE)，其中DV包含已被分配但其邻居尚未被完全分配的顶点，以及已经被探测到的但尚未被分配的顶点。DE包含原图数据中的反向边，因此当分配顶点时，可以在动态反向映射图中，直接通过当前顶点的单一记录，得知分配当前顶点可利用的边和点的信息。

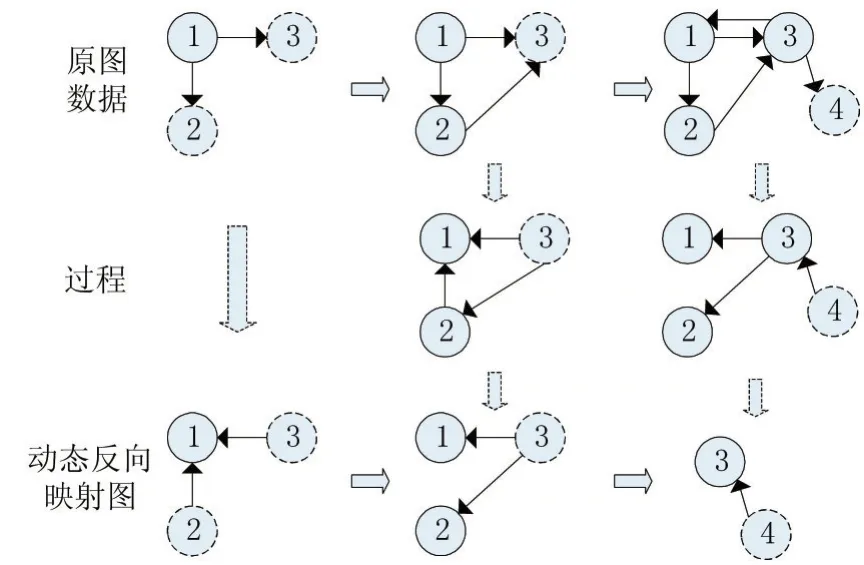
图2 动态反向映射图示例

图中虚线顶点代表尚未分配顶点，实线顶点代表已被分配顶点。

当顶点1到来时，还带有其邻居3和邻居2，但此时并不知道2和3的邻居，也不知道其邻居信息什么时间会到来，只能将此条数据反向存储起来，以备后用。当顶点2到来，带有其邻居3，同顶点1的处理方式相同，将2和3反向存储起来，检测到此时2已经被分配完毕，所以反向映射图中的顶点2的出度边去除，因为在未来的分配过程中将不会再用到反向映射图中的顶点2的出度边，以控制作为辅助数据的动态反向映射图的规模的增长；同理，顶点3到来时，将其与顶点4相连的边存入动态反响映射图，同时3的出度边被去除，而此时顶点1和顶点2已经成为了孤立的顶点，所以也被去除。

2.3 有向图划分

流图划分的基本框架假定一序列的输入以及一个单一的装载器，并且顶点一旦确认分配位置，就不再更改，即是所谓的一次遍历划分。但一次遍历自然会在处理有向图时产生信息的丢失，故本文在此框架基础上提出基于动态反响映射图的流图划分算法（SGPD⁃MG），通过动态反向映射图来收集起始顶点的部分入度边并确保无出度顶点不被遗漏。SGPDMG算法是基于顶点的图划分算法，输入序列中的一个元组包括当前顶点以及其邻居信息，本文使用μ来表示。

传统的图划分算法有两个输入，边集E，顶点集V，流图划分算法无法利用这两个数据输入，数据输入变为了G'=(V',E)，其中V'为有出度定点的集合，本文的算法就是利用此“不完整”的数据输入，在不增加图数据的遍历次数的前提下，用一次遍历的方式达到更优的分配效果。

算法1：基于动态反向映射图的流图划分算法(Streaming Graph Partition based on Dynamic inverse Mapping Graph,SGPDMG)输入：G'=(V',E),分区数k.

输出：将每一个顶点映射到关联的分区,M(v)∈[k].

步骤:

2.4 启发式函数

为了以流式图划分的过程达到平衡图划分的两个目标，启发式函数利用了图的两个信息，分别是各个分区的空闲程度，以及当前顶点在各个分区的邻居数量。显然，当某个分区的空闲程度越大，邻居数量越多，将当前顶点分配到该分区的趋势就越大。由此，Stanton 2013的权重确定性贪心算法（LDG）提出了如下形式的公式：

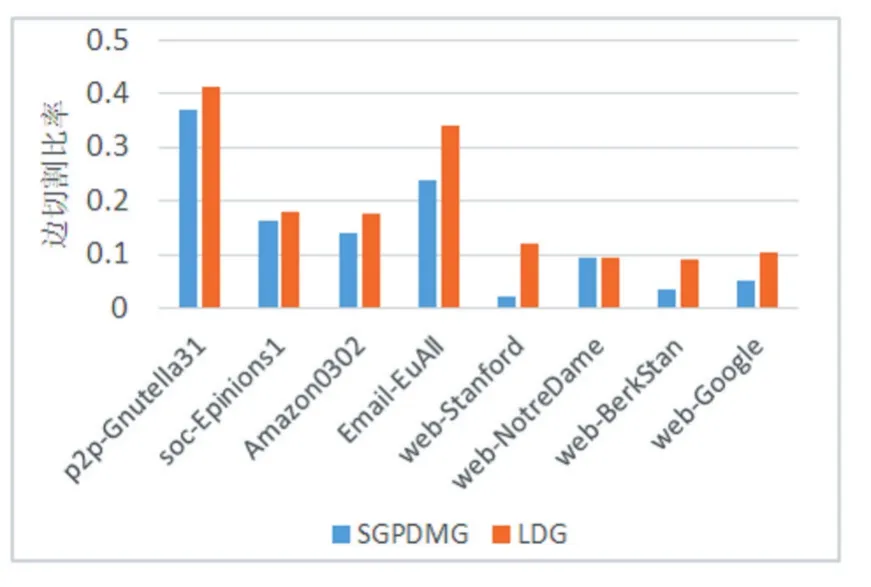
图3 边切割比率对比，k=4

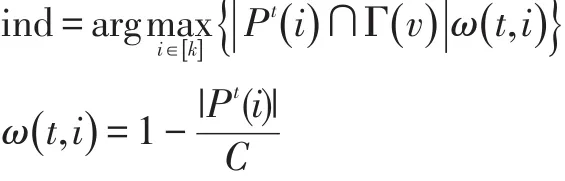
其中ind即为当前顶点要分配到的分区的编号，符号Pt代表时间t时的分区集。每一个独立的分区由Pt(i)表示，所以等于所有已被分配的顶点。v表示在时间t，流中来到的顶点，Γ(v)代表顶点v的所有邻居，|S|表示集合S中的元素数量，C是每个分区上的容量限制。

3 实验

有向图许多都会存在没有出度的顶点，表1是对实验图数据中有出度顶点数目的统计，实验数据来自于斯坦福大型网络数据集收集网站[13]。可以看出，有部分图数据有出度顶点的占比时非常之低的，例如p2p-Gnutella31只有26.18%，而WikiTalk只有6.16%。

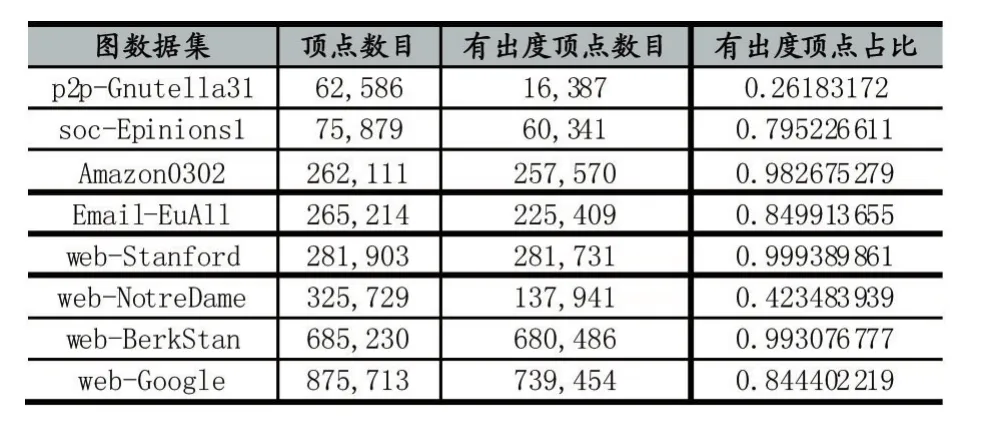
表1 图数据中有出度顶点与总顶点数对比

图划分算法最重要的评价指标是边切割比率，图3、图4和图5的实验中可以看出本文提出的算法在不同的k值下，都能取得更好的划分结果。实验中效果最好的web-Stanford数据集不是无出度顶点占比最大的数据集，可以看出即便是只有少量的无出度顶点，对其的忽略也有可能产生巨大的结果影响。

图4 边切割比率，k=8

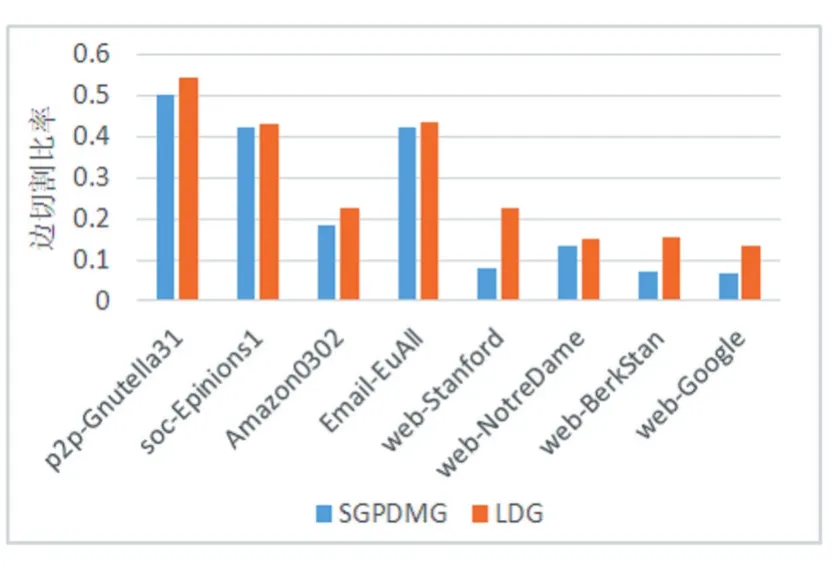
图5 边切割比率，k=16

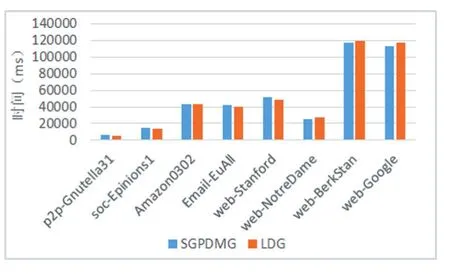
图6 算法消耗时间对比

算法追求效果的同时，也需要考察其执行时间，图6的实验展示了算法的消耗时间，可以看出本文提出的算法在时间消耗上并不处于劣势。

参考文献：

[1]L.Hyafil，R.Rivest.Graph Partitioning and Constructing Optimal Decision Trees are PolynomialComplete Problems[R].Technical Report 33,IRIA-Laboratoire de Recherche en Informatique et Automatique,1973.

[2]M.R.Garey,D.S.Johnson,L.Stockmeyer.Some Simplified NP-Complete Problems[C].In 6th ACM Symposium on Theory of Computing,STOC.ACM，1974：47-63.

[3]B.W.Kernighan and S.Lin.An Efficient Heuristic for Artitioning Graphs[J].Bell Sys.Tech.Journal,49:291-308,1970.

[4]C.M.Fiduccia，R.M.Mattheyses.A Linear Time Heuristic for Improving Network Partitions[C].In 19th IEEE Design Automation Conference,1982：175-181.

[5]G.Karypis and V.Kumar.A Fast and High Quality Multilevel Scheme for Partitioning Irregular Graphs[C].In ICPP,1995：113-122.

[6]B.Hendrickson，R.Leland.A Multilevel Algorithm For Partitioning Graphs[J].In Supercomputing,1995.

[7]George Karypis，Vipin Kumar.A Parallel Algorithm for Multilevel Graph Partitioning and Sparse Matrix Ordering[J].Journal of Parallel and Distributed Computing,1998:48(1):71-95.

[8]Isabelle Stanton，Gabriel Kliot.Streaming Graph Partitioning for Large Distributed Graphs[P].In Proc.Of KDD Conference,2012:1222-1230.

[9]Charalampos E.Tsourakakis,Christos Gkantsidis,Boˇzidar Radunovi'c,and Milan Vojnovi'c.Fennel:Streaming Graph Partitioning for Massive Scale Graphs[R].Technical report,Microsoft,2012.

[10]Joel Nishimura，Johan Ugander.Restreaming Graph Partitioning:Simple Versatile Algorithms for Advanced Balancing[P].In Proc.of SIGKDD conference,2013：1106-1114.

[11]N.Xu,B.Cui,L.-n.Chen,Z.Huang,Y.Shao.Heterogeneous Environment Aware Streaming Graph Partitioning[J].TKDE,2015.

[12]Robert Krauthgamer,Joseph(Seffi)Naory,Roy Schwartzz and Kunal Talwarx.Non-Uniform Graph Patitioning[C].Acm-siam Symposium on Discrete Algorithms,2014:1229-1243.

[13]http://snap.stanford.edu/data/index.html