光纤耦合器的激光多普勒信号相位解调

张雄星，郝冬杰，王 伟，王可宁，范 源

(西安工业大学光电工程学院，陕西 西安 710021)

0 引言

激光干涉测速技术[1]常用的相位解调算法有3×3光纤耦合器相位解调算法[2-3]和希尔伯特变换算法[4-5]。希尔伯特变换算法是对原始信号相移90°，得到两路正交信号，然后通过反正切函数计算信号相位。3×3光纤耦合器相位解调算法利用三路相位差为120°的多普勒信号微分交叉相乘法，得到两路正交信号，然后通过反正切函数计算信号相位。由于3×3光纤耦合器很难实现完全对称，再加上很难保证光电探测器的工作效率一致、光路中的元件耦合损失等原因[6-7]，因此，在信号解调过程中，需要在三路探测器的输出端加上不同的增益，进而使三路信号达到平衡。为此，本文采用3×3光纤耦合器相位解调算法对其进行解算。

1 3×3光纤耦合器相位解调算法

1.1 系统检测原理

全光纤激光多普勒测速系统主要包括半导体激光器、光纤隔离器、光纤耦合分束器、光纤环形器、准直器和探测器等光学器件。系统原理如图1所示。

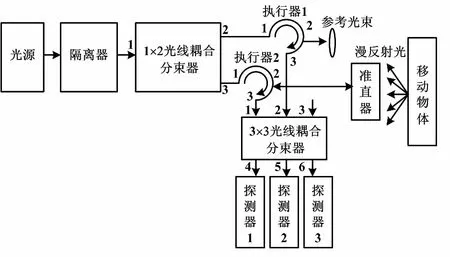
图1 系统原理图 Fig.1 Schematic diagram of the system

激光器发出的光，通过光纤隔离器进入1×2 光纤耦合器分束器分为两束。其中一束光从1×2光纤耦合器端口2进入第一个环行器，从第一个环行器端口2输出的光进入光纤反射镜，光纤反射镜反回的光从第一个环行器端口3端口输出作为参考光。另一束光从1×2光纤耦合器端口3进入第2个环行器，由第2个环行器2端口进入光纤准直器，经过准直器后照射运动目标。反射光经过第2个环行器端口3输出，输出的光作为信号光；参考光和信号光在3×3光纤耦合器中进行干涉，从3×3光纤耦合器输出的多普勒光信号通过3路光电探测器，把多普勒光信号转换成位电信号。

1.2 3×3 光纤耦合器相位解调原理

对于理想的3×3光纤耦合器，光纤耦合器输出的三路信号经光电转换后为：

(1)

式中：I1、I2、I3分别为三路探测器输出的光电流；R为光电探测器的灵敏度；PL为参考光功率；Ps为信号光功率；φ(t)为参考光与信号光的相位差[8]。

光电探测器的光电流(多普勒信号)经跨阻放大电路转化为电压信号，将电压信号进一步放大，电压信号分别为u1、u2、u3。当3×3 光纤耦合器是完全对称并且无损失时，三路多普勒信号的相位差是120°，因此，正交信号可以从(u1,u3-u2)获得。多普勒信号相位为：

(2)

相位调制也可以表示为频率调制，相位φ(t)对时间求导数，可以得到相应的多普勒频移fD，由相应的关系式可得：

(3)

振动物体的径向速度由下式确定：

(4)

2 试验验证

2.1 仿真验证

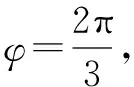
(5)

图2为加入20 dB随机白噪声后的多普勒信号。图2中:1～3路分别为多普勒信号。

图2 加噪后的多普勒信号仿真图 Fig.2 Simulation of the noise-added Doppler signal

选用其中一路多普勒信号，采用希尔伯特变换对多普勒信号x1(t)移相90°,可以得到正交信号y(t)。其表达式为：

y(t)=-sin(5 000πt)+e(n)

(6)

希尔伯特变换变换后，求得相位的表达式为：

(7)

通过希尔伯特变换后获得的移相前后多普勒信号仿真图如图3所示。图3中：1路为希尔伯特变换后的多普勒信号；2路为原始多普勒信号。希尔伯特变换后相位误差如图4所示。仿真结果证明：当信噪比为20 dB时，希尔伯特变换的相位误差约为5°。

图3 多普勒信号仿真图 Fig.3 Simulation of the Doppler signal

图4 希尔伯特变换相位误差图 Fig.4 Phase error of Hilbert transformation

采用3×3 光纤耦合器相位解调算法，相位误差如图5所示。仿真结果证明：当信噪比为20 dB时，3×3 光纤耦合器相位解调算法的相位误差约为0.6°。

图5 3×3 光纤耦合器算法相位误差图 Fig.5 Phase error of 3×3 fiber optic coupler algorithm

从以上两组数据测得的相位误差可以得出，希尔伯特变换后获得的相位误差大于3×3 光纤耦合器相位解调算法的相位误差。

当多普勒信号的信噪比降低时，3×3 光纤耦合器相位解调算法的相位误差增大不明显，而希尔伯特变换的相位误差显著增大，体现了3×3 光纤耦合器相位解调算法对噪声良好的容忍能力。不同信噪比下，两种相位解调算法的相位测量误差如表1所示。

表1 相位测量误差Tab.1 Phase measurement error

从表1可知，当信噪比越低时，希尔伯特变换算法的相位误差越大，而3×3 光纤耦合器相位解调算法的相位误差在4°的范围内，对噪声的容忍性强。

2.2 试验验证

试验时，搭建了激光多普勒测速平台，使用音叉作为待测物体。试验所用1 550 nm半导体激光器，光路采用全光纤光路，光电探测器采用自制的铟钾砷InGaAs去偏探测器[9]。

经光电探测器转换后，输出多普勒信号的相位差、直流量系数以及交流量系数是由解调电路本身的硬件结构和器件特性决定的[10]。3个通道很难输出完全一致的波形。在信号解调中，通过改变探测器的增益，使输出的三路多普勒信号相等。

分别采用希尔伯特变换相位解调算法和3×3 光纤耦合器相位解调算法，编写多普勒信号速度解算程序。通过上位机观察速度解算结果。希尔伯特变换和3×3 光纤耦合器的相位解算速度波形如图6所示。

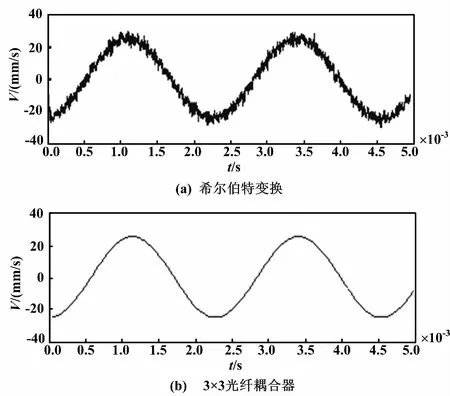
图6 相位解算速度波形图 Fig.6 Diagram of phase calculation velocity waveform

从图6可以看出， 3×3光纤耦合器相位解调算法解算的振动速度曲线更光滑，对噪声容忍度更高。试验采用的音叉固有频率为440 Hz，测速系统输出的速度信号的频率为441.2 Hz。试验结果表明，系统误差为0.27%。

3 结束语

本文针对低信噪比多普勒信号的速度解算，提出一种基于3×3光纤耦合器的激光多普勒信号相位解调方法。通过仿真和实测与传统的希尔伯特变换相位解调方法相比较，得出以下结论：3×3光纤耦合器相位解调算法适合于低信噪比的场合，对噪声容忍度更高；可用于超低频振动测量或者低速运动目标的测量。

参考文献:

[1] 彭其先. 分时激光干涉测速技术[D].成都：中国工程物理研究院,2009.

[2] BAUER M,RITTER F,SIEGMUND G. High-precision laser vibrometers based on digital Doppler signal processing[J].

Proceeding Spie,2002,48(27):50-61.

[3] 钟志,谭久彬. 激光干涉快速超精密测量残余累计误差研究[J]. 光电子·激光,2005(3):328-331.

[4] 肖剑,柳斌,郭亚龙,等. 基于希尔伯特变换的干涉仪信号处理[J]. 探测与控制学报,2010(1):80-83.

[5] GRECHIKHIN V A,RINKEVICHIUS B S. Digital hilbert transform for processing of laser doppler vibrometer signals[C]//International Conference on Vibration Measurements by Laser Techniques,1996:89-96.

[6] 曾周末,刘芳,封皓,等.基于3×3耦合器的双马赫-曾德尔干涉仪数字化相位解调[J].光学精密工程,2014(6):1410-1417.

[7] CHAPMAN M,ATTWOOD L.Heterodyne and homodyne interferometry[EB/OL].[2012-03-01]. http://www. renishaw. com.

[8] 穆姝慧,俞本立.光纤干涉仪中用于消除偏振衰落的平衡检测技术[J].大学物理,2008(11):34-36.

[9] 郑龙. CO2连续波差分吸收激光雷达信号检测及数值处理[D].上海：中国科学院研究生院,2014.

[10]陈宇,林京,孟强.基于3×3耦合器光纤水听器的数字化解调方案[J].仪器仪表学报,2008(4):755-759.