基于残余动量时频特征和SVM的机械臂故障分类研究

王 帅，邵丹璐，王 凌，张 云，王斌锐

(中国计量大学机电工程学院，浙江 杭州 310018)

0 引言

电机故障是机械臂作业过程中的常见故障之一。在机械臂运行中，对电机故障进行检测是及时发现故障和安全作业的前提[1-2]。对机械臂故障的准确分类可为有效排除机械臂故障提供支撑[3-4]。

Alessandro等[5]提出一种将环境故障通过残差形式表现的方法。由于残差计算需基于精确的系统模型，因此鲁棒性较差。K.Suita等[6]通过对比实际驱动器力矩与模型计算得出的力矩，检测机械臂是否发生故障；Trevor等[7]基于统计学学习方法，研究了支持向量机(support vector machine，SVM)在故障分类问题中的应用。Felzenszwalb等[8-9]用支持向量机来设计分类器，构建故障检测算法，目标检测的准确率相对较高。邵丹璐等[10]基于动量导数，设计了残余动量算子，通过分析碰撞中残余动量值的变化来检测柔性臂是否发生碰撞故障。万书亭等[11]提出了一种基于提升模式的非抽样小波变换方法。该方法用于对数据信号进行分类处理，对滚动轴承故障能作出有效诊断，但缺乏对故障发生过程的分析。

本文以三自由度机械臂的电机故障为检测对象，通过支持向量机训练分类器，得到残余动量在频域中的特征向量，并与时域特征向量相结合。通过分析故障源与特征向量变化之间的关系检测故障，搭建机械臂虚拟样机联合仿真平台，开展故障检测仿真。对工业机器人开展了试验验证。通过仿真和试验，验证了故障检测和分类的有效性。

1 残余动量信号特征提取

1.1 残余动量的定义

动力学建模是数学分析的基础。参考文献[12]建立的机械臂动力学模型为：

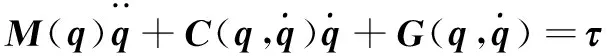
(1)

根据文献[13]定义残余动量算子r为：

(2)

式中：放大系数k为大于零的对角阵；p为机械臂的总

能量。

当机械臂与环境发生碰撞时：

(3)

式中：τ为碰撞力矩。

式(2)求导后满足：

(4)

1.2 时域特征

提取特征向量可降低计算的难度，便于进行故障检测和分类。残余动量是一维时变信号，本文采用均值、方差和相关系数组成时域特征向量。

三自由机械臂残余动量的均值为：

D=[D1,D1,D3]

(5)

方差为：

C=[C1,C2,C3]

(6)

相关系数表示残余动量值之间的相似性。三自由机械臂残余动量的相关系数为：

ρ=[ρ12,ρ23,ρ13]

(7)

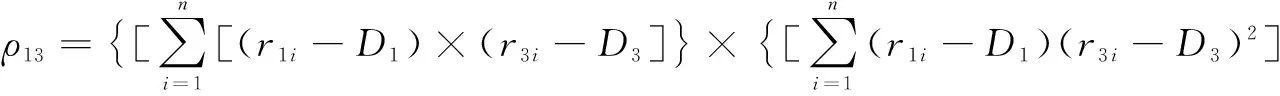
1.3 频域特征

(8)

式中：N为数据长度；j=1,2,…,2k为分解频带的序号；rjm为重构信号离散点的幅值。

分解层数与计算量有密切关系。为便于计算，选定分解层数k。

三自由机械臂残余动量的小波包能量谱为：

T=[Er1,Er2,Er3]

(9)

小波包能量谱T共有3×8=24个特征值，时域的均值D、方差C和相关系数ρ共有3×3=9个特征值。

2 机械臂电机故障检测与分类仿真

2.1 联合仿真模型

本文基于ADAMS和Simulink，搭建了完整的虚拟样机仿真平台，如图1所示。

虚拟样机的输入为3个关节的力矩，输出为3个关节的角度和角速度，从而便于电机故障模拟和残余动量计算。

ADAMS模型参数如表1所示。

图1 虚拟样机仿真平台 Fig.1 Virtual prototype simulation platform 表1 ADAMS模型参数Tab.1 ADAMS model parameters

模型长度/mm平均直径/mm质量/kg大臂31382.8017.78小臂23779.2013.10基座500100.0099.00

机械臂电机故障有多种，忽略基座故障，本文研究的机械臂故障分类如表2所示。

“哎呀，我们杨连长真细心，妹子，快接着。我说有沙枣花吧？你看一串一串的花苞，要开了。”女人的话还没落地，一片掌声撵出一片哄笑，田志芳面对这突发的一切，有点不知所措。“跑了这么多天的长途路，终于到家了，妹子，肯定累了，走吧，到你住宿地方休息去。”

表2 机械臂故障分类Tab.2 Fault classification of manipulator

通过人为设置故障和联合仿真，得到残余动量值样本。利用得到的故障数据样本，采用基于核函数的非线性软间隔分类器，即C-支持向量分类机，对出现的故障进行分类。

2.2 残余动量仿真计算和特征提取

本文通过联合仿真，共采集200组残余动量值，其中，机械臂正常状态数据80组，其余六种故障数据各20组。根据式(5)～式(7)和式(9)计算，并作归一化处理，样本数据的均值、方差、相关系数如图2所示。部分样本小波包能量谱如图3所示。由图2可见，时域特征值变化剧烈且无明显规律，所以仅从单个时域特征值的变化无法分类故障。由图3可见，不同故障下的小波包能量谱图有显著区别，但规律性不明显。因此，需要将多个特征值综合应用于故障分类。

图2 均值、方差、相关系数图 Fig.2 The mean,variance and correlation coefficient

图3 部分样本小波包能量谱图 Fig.3 Partial sample wavelet packet energy spectrum

2.3 支持向量机SVM分类

本文任意选取200个样本中的100个作为训练样本，其余样本作为测试样本。基于Libsvm工具包，本文采用径向基核函数，通过交叉验证法，自动寻优确定最优的惩罚因子c=512和核函数的参数γ=0.007 8。测试样本的故障分类准确率如表3所示。

表3 不同特征向量分类准确率Tab.3 Classification accuracy of different feature vectors

采用时域和频域特征值进行故障分类，其准确率高于仅采用时域特征值的故障分类。

3 机械臂故障分类试验

正常运动试验结果如图4所示。

图4 正常运动试验结果图 Fig.4 Experimental results of normal motion

试验采用工业机器臂，其控制系统如图5所示。

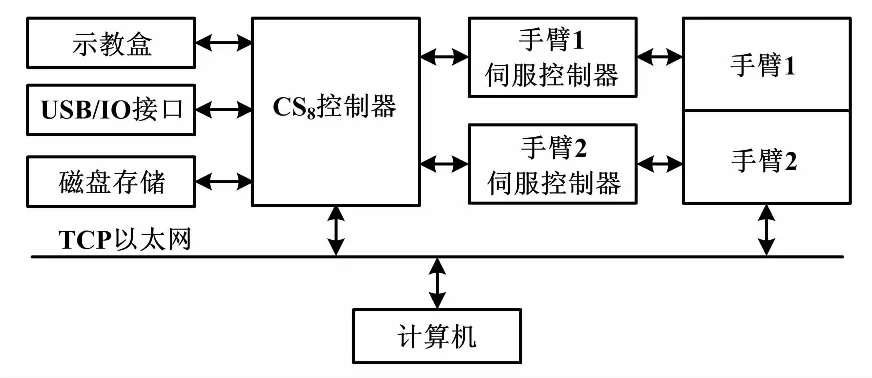
图5 机械臂控制系统框图 Fig.5 Block diagram of manipulator control system

碰撞故障试验结果如图6所示。

图6 碰撞故障试验结果图 Fig.6 Experimental results of collision fault

对机械臂的第2、3关节运动进行试验。设关节2为手臂1，关节3为手臂2，其余关节锁定。试验过程中，控制手臂1和手臂2逆时针运动30°，并通过在机械臂运动空间中放置工作台来人为制造碰撞故障。采集机械臂运行过程中的角度和角速度数据，计算得到残余动量值。

对比图5和图6可见，正常运动时残余动量值的波形周期性变化明显。当发生碰撞时，残余动量值有明显突变。试验中，计算并提取到的时域和频域的特征值如表4所示。由于工业机械臂封装严格，电机异常振动和噪声故障试验困难。

本文重复上述正常和碰撞故障两类试验，并在不同时间点人为制造碰撞故障。将试验中测得的残余动量时域和频域特征值输入到SVM分类器。测试结果表明，碰撞故障检测准确率为100%。

表4 试验所得特征向量Tab.4 Eigenvector obtained by experiments

4 结束语

本文基于残余动量对机械臂的故障进行检测与分类，对残余动量信号的特征提取分类进行了详细的分析。最后通过仿真和试验进行了验证，结果如下。

①电机异常振动、噪声以及碰撞故障会使得残余动量值发生变化。但单独的时域或频域特征值变化与故障类型之间无明显规律。

②综合利用残余动量值的时域和频域特征进行故障分类，可以得到较高的准确率。

③设计的基于支持向量机分类算法能够对多关节机械臂、高维的残余动量时频特征向量进行分类。

下一步研究将丰富故障的种类，并对分类器进行优化设计。

参考文献:

[1] SHI J,LIANG M,GUAN Y.Bearing fault diagnosis under variable rotational speed via the joint application of windowed fractal dimension transform and generalized demodulation:a method free from prefiltering andresampling[J].Mechanical Systems and Signal Processing,2016,68(1):15-33.

[2] BRKOVIC A,GAJIC D,GLIGORIGEVIC J,et al.Early fault detection and diagnosis in bearings for more efficient operation of rotating machinery[J].Energy,2017,136(11):63-71.

[3] 曾艳涛.美国未来15年制造业机器人研究路线[J].机器人技术与应用,2013(3):1-5.

[4] GAN M,WANG C.Construction of hierarchical diagnosis network based on deep learning and its application in the fault pattern recognition of rolling element bearings[J].Mechanical Systems and Signal Processing,2016,72(9):92-104.

[5] DE L A,FERRAJOLI L.Exploiting robot redundancy in collision detection and reaction[C]//Intelligent Robots and Systems,IROS 2008.IEEE/RSJ International Conference on IEEE,2008:3299-3305.

[6] SUITA K,YAMADA Y,TSUCHIDA N,et al.A failure-to-safety "Kyozon" system with simple contact detection and stop capabilities for safe human-autonomous robot coexistence[C]//Robotics and Automation,IEEE International Conference on,IEEE,1995:3089-3096.

[7] HASTIE T,TIBSHIRANI R,FRIEDMAN J.The elements of statistical learning:data mining,inference and prediction[J].Mathematical Intelligencer,2005,27(2):83-85.

[8] FELZENSZWALB P F,GIRSHICK R B,MCALLESTER D.Cascade object detection with deformable part models[C]//Computer Vision and Pattern Recognition (CVPR),2010 IEEE Conference on IEEE,2010:2241-2248.

[9] GIRSHICK R B,FEIZENSZWALB P F,MCALLESTER D.Object detection with grammar models[C]//International Conference on Neural Information Processing Systems,Curran Associates Incorporation，2011:442-450.

[10]邵丹璐,王斌锐,金英连.基于残余动量的两连杆柔性臂驱动器故障检测[J].计量学报,2015,36(3):279-283.

[11]万书亭,吕路勇,何玉灵.基于提升模式非抽样小波变换的滚动轴承故障诊断方法研究[J].振动与冲击,2009(1):170-173.

[12]温金环.三关节六自由度机械臂运动学及动力学分析和不确定刚性机器人的鲁棒轨迹跟踪控制研究[D].西安:西北工业大学,2002.

[13]DE L A,FLACCO F.Integrated control for pHRI:Collision avoidance,detection,reaction and collaboration[C]//Biomedical Robotics and Biomechatronics (BioRob),2012 4th IEEE, RAS & EMBS International Conference on,IEEE,2012:288-295.

[14]GILLES J.Empirical wavelet transform[J].IEEE Transactions on Signal Processing,2013,61(16):3999-4010.

[15]何学文,卜英勇.基于小波包分解和支持向量机的机械故障诊断方法[J].机械强度,2004,26(1):20-24.