动态矩阵控制算法的仿真研究及PLC应用
吴海中,田 沛
(华北电力大学控制与计算机工程学院,河北 保定 071003)
0 引言
工业生产中,一些惯性较大的系统具有非线性、时变等[1]特点,容易被各种因素干扰。尤其是近年来电厂向大容量发电机组发展[2],对控制系统的要求越来越高,传统PID算法已难以满足工业生产的需要[3]。而基于传统方法的系统模型最优控制方案,在工业现场往往无法实现最优控制[4]。由于预测控制对被控对象模型要求不高,现代控制理论很难在过程工业中得到广泛应用[5],其主要原因就是需要高精度的对象模型。而预测控制无需对控制过程的内部机理进行深入研究,这就简化了最小化参数模型辨识的复杂度[6]。
本文采用动态矩阵控制(dynamic matrix control,DMC)算法,对主汽温系统进行控制,设计了DMC-PID串级控制系统,并进行多模型预测控制仿真,将DMC算法封装到PLC中。试验结果表明,较PID,DMC控制具有更优的控制效果。
1 动态矩阵预测控制
在20世纪后期,Culter提出了动态矩阵控制算法[7-8]。它是一种基于系统的单位阶跃响应序列的控制策略。
动态矩阵控制算法一般分为3部分:预测模型、滚动优化、反馈校正[9]。
1.1 预测模型
DMC算法中,首先采样得到被控对象阶跃响应的序列ai=a(iT),i=1,2,…,N。其中:T为采样周期;N为模型时域长度。有限集合a={a1,a2,…,aN}构成动态矩阵控制的模型参数,称为预测模型向量。
根据线性系统的比例性质和叠加性质,可用模型向量预测未来各时刻被控对象的任意输入的输出值,可得预测模型:
YM(k+1)=AΔU(k)+A0U(k-1)
(1)

1.2 滚动优化
动态矩阵控制是一种优化控制策略,最优控制律根据二次型性能指标[10]确定。
(2)
式中:R为控制量加权矩阵;Q为输出预测误差加权矩阵。
对∂Jp/∂U(k)=0化简,得:
ΔU(k)=(ATQA+R)-1ATQ[Wp(k)-yp0(k)]
(3)
事实上,在kT时刻,只有Δu(k)对对象有作用,即:
Δu(k)=cTΔU(k)
(4)
1.3 反馈校正
由于存在预测模型失配[11]和环境干扰等未知因素,动态矩阵在每一步运算后,可用预测误差e(k)修正每步预测值,达到反馈校正的效果。即:
Yp(k+1)=YM(k+1)+he(k)
(5)
式中:e(k)=y(k)-ym(k)和h=[h1,h2,…,hN]称为校正向量。
下一时刻的初始预测值可设为:
Y0(k+1)=sYp(k+1)
(6)
2 仿真研究
2.1 DMC算法的实现
某电厂660 MW直流锅炉在50%、70%、90%、100%负荷下,主汽温对象在减温水喷水作用下的动态特性对象模型如表1所示[12]。
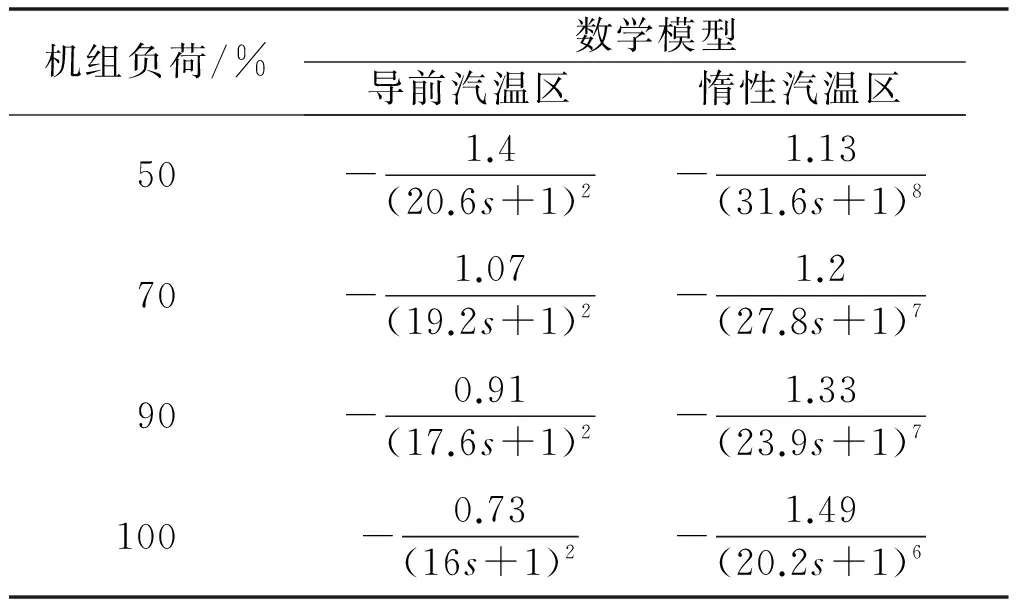
表1 主汽温在不同负荷下的数学模型Tab.1 Mathematical model of main steam temperaturesystem under different loads
火电厂主汽温系统是一个具有大延迟、大惯性等特性的对象。由于过热器管道较长,从控制减温水流量到蒸汽温度变化的过程有较大的迟延,且主蒸汽温度的对象动态特性受负荷变化的影响较大[13]。对100%负荷下的对象模型进行仿真。设定模型时域长度N=90,采样周期T=4 s,控制时域长度M=5,优化时域长度P=20,控制权系数λ=1,设定值pv=1。以上对象用粒子群算法进行优化,得到PID控制参数δ=2.43、Ti=31。
仿真所得的DMC与PID单位阶跃定值扰动响应曲线如图1所示。与传统PID控制相比,DMC控制的系统输出响应速度更快、调整时间更短、系统响超调更小。在系统输入方面,DMC控制有明显的优势。在实际生产中,控制器输出的大小和频率需要在允许的范围内。

图1 单位阶跃定值扰动响应曲线 Fig.1 Step response curves of fixed value disturbance
2.2 参数分析
与PID算法相比,动态矩阵控制算法提高了被控对象的阶次变动以及对象时滞的鲁棒性[14],取得了较好的控制品质。为了分析每个控制参数对系统控制效果的影响,保持其他控制参数不变,变动某单一参数对比分析输出曲线。考虑控制器输出和偏差2个因素,性能指标公式如下:

(7)
①采样周期T和模型长度N。
为了使非参数模型包含更多的被控对象动态信息,即要求在NT时刻的阶跃响应值能够无限接近稳态值,因此需要NT取值尽量大。当采样周期一定时,N的增大会大大增加运算量;T需要在允许的范围内,T的增大会导致抗干扰能力变弱。
②预测时域长度P。
预测时域长度与系统的快速性和稳定性有关,预测时域长度应该包含对象的主要动态信息。若P太小,虽然控制系统快速性更好,但是降低了系统的鲁棒性和稳定性;若P太大,虽然提高了系统的动态性能,但是系统响应变慢,系统的实时性变差。
③控制时域长度M。
控制时域长度M指的是优化变量个数。M过小,会导致系统输出难以保证紧密跟踪期望值,响应慢,但系统鲁棒性和控制稳定性较好;M太大,可改善系统动态响应,机动性更强,但是稳定性变差。所以,M的选择需要衡量系统的稳定性和快速性。
2.3 DMC-PID串级控制系统
由于DMC控制设定的采样周期一般较大,对突发性的随机干扰难以及时控制。常规串级PID控制系统的抗干扰能力比较强。因此,将DMC控制与PID控制结合,设计DMC-PID串级控制系统,充分发挥DMC对大延迟、大惯性对象适应能力强和PID抗干扰能力强的优点。DMC-PID串级结构如图2所示。

图2 DMC-PID串级结构图 Fig.2 DMC-PID cascade control structure
图2中:R为过热器出口汽温设定值;y2为主蒸汽导前温度;y1为过热器出口汽温的实际值;W01为主汽温系统惰性区数学模型;W02为主汽温系统导前区数学模型。
副回路采用常规P调节控制器,与导前区对象构成副回路控制结构。主回路采用DMC控制器,预测主汽温的变化趋势,实现温度的提前控制,改善主汽温大延迟、大惯性的特性。

在主汽温DMC-PID串级控制系统中,主控制器的采样周期T=4 s,模型时域长度N=90,优化时域长度P=20,控制时域长度M=5,控制权系数λ=1;副控制器Kp=0.49,Ti=61。在副控制器输出加入定值干扰,DMC-PID和PID-PID串级控制系统仿真响应曲线如图3所示。对比结果表明:DMC-PID串级控制系统响应速度快,过渡时间较短,没有明显超调,并具有较好的抗干扰能力。

图3 串级控制仿真曲线 Fig.3 Cascade control simulation curves
2.4 多模型动态矩阵控制
随着工业生产的控制要求越来越高,只有单一模型的预测控制器已无法满足复杂工业生产的控制要求。多模型预测控制使用多个对象模型来逼近真实系统,然后在多个对象模型的基础上设计控制器。多模型预测控制的难点不在于预测控制算法的运用,而在于切换或者加权策略的选择。
本文的多模型动态矩阵控制采用模型切换策略。在假设已知模型切换时刻的情况下,重新构造系统的多步预测动态矩阵A,从而得到平滑切换的效果[15]。假定在k0时刻系统切换模型:当k>k0时,对象模型为M2;当k≤k0时,对象模型为M1。当k≤k0-P时,选择模型M1计算系统预测输出;当k>k0+P时,选择模型M2求取系统预测输出;当k0
分别取某电厂机组50%负荷和70%负荷时的模型,记为M1、M2,设定值由1切换到1.5,多模型动态矩阵控制仿真曲线如图4所示。添加以上切换策略,可以实现平滑切换。
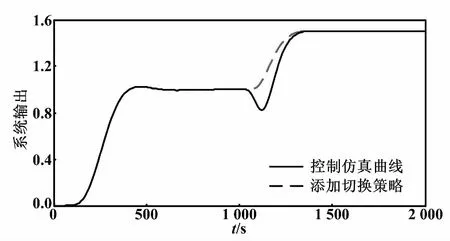
图4 多模型动态矩阵控制仿真曲线 Fig.4 Multi-model dynamic matrix control simulation curves
3 工程应用
针对电厂的实际使用情况,本文利用西门子S7-300 PLC的S7-SCL语言,将DMC算法封装成可供用户调用的FB功能块,完成了DMC算法的PLC实现。使用MODBUS协议与原来的控制系统进行数据通信,起到优化控制的效果。
对于封装后的DMC模块,本文设计了2个数字量输入端和9个模拟量输入端,以及DMC模块对应的背景数据块DB350。由于被控对象是时变对象,受很多因素干扰,容易导致模型失配。为此,对DMC模块设计了K、T、N和TAO输入端,可以输入实时辨识对象,使模块更具实时性。封装后的DMC模块增加了实际工程应用的特性,能运算先进的控制算法。当TRACKON=FALSE时,模块为自动控制状态;当TRACKON=TRUE时,模块为跟踪状态。
针对荥阳电厂主汽温对象模型,配合国电智深EDPF-NT Plus DCS系统,使用DMC模块进行优化控制。通过粒子群算法优化其控制参数,可得参数为N=90、P=25、M=5,并取q=1、r=0.5、T=3 s;主蒸汽温度设定值为540、运算周期为5 s。在优化参数基础上进行调试,得到的系统主蒸汽温度输出和减温喷水阀门开度的系统输出实时趋势图如图5所示。

图5 系统输出实时趋势图 Fig.5 Real-time system output trends
截取部分历史数据可知:前段主汽温稳定保持在540 ℃,减温喷水阀门开度为53.2%;然后,主汽温设定为520 ℃,控制阀门反应较快,减温喷水阀门的开度变大;主汽温对象经过一段时间后,稳定在520 ℃,减温喷水阀门开度也慢慢稳定在55.37%。由图5可以看出,DMC控制快速性好,超调小;DMC控制量输出,即减温喷水阀门的动作并没有很剧烈。
4 结束语
本文利用西门子S7-300 PLC的S7-SCL语言,将DMC算法封装成可供用户调用的FB功能块,完成了DMC算法的PLC实现,并对主汽温系统设计了DMC-PID串级控制结构。大量测试试验表明,较传统PID控制,主汽温控制系统的稳定性、快速性有了较大提高。但在实际工程应用中,需要继续考虑多变量多模型预测控制、非线性、手/自动无扰切换、克服干扰等实际工程问题。
参考文献:
[1] 何德峰,黄骅,余世明.时变非线性不确定系统H∞鲁棒模型预测控制[J].控制与决策,2014,29(12):2265-2270.
[2] 李续军,朱宝田,谢冰,等.高参数大容量火电机组汽轮机和锅炉主蒸汽参数的匹配关系[J].电力标准化与计量,2003,12(3):26-32.
[3] 张嘉英,席东民,胡琳静.广义预测控制在锅炉燃烧控制系统中的应用[J].热力发电,2011,40(2):56-59.
[4] 赵军.采用专家控制算法提高火电机组自动控制品质[J].热力发电,2007,36(10):52-56.
[5] 席裕庚,李德伟.预测控制定性综合理论的基本思路和研究现状[J].自动化学报,2008,34(10):1225-1234.
[6] 高山.300 MW机组主汽温系统预测控制方案研究[D].北京:华北电力大学,2015.
[7] 安爱民,杨国强,张浩琛,等.基于T-S模糊决策的PMSG风电系统广义预测控制[J].自动化仪表,2016,37(9):1-5.
[8] 潘岩,潘维加.动态矩阵预测控制在火电厂中的应用与展
望[J].自动化仪表,2014,35(11):17-19.
[9] 郭伟,夏友亮,周丽,等.多变量动态矩阵控制算法研究[J].计算机仿真,2014,31(8):360-363.
[10]王进华.二次型最优控制问题中的权矩阵与最优控制律[J].控制与决策,2007,22(8):943-945.
[11]张文安,徐建明,俞立.PID-DMC算法及其在液位控制系统中的应用[J].控制工程,2005,12(1):22-24.
[12]叶向前,崔春雷,易凤飞,等.基于改进型动态矩阵预测的主蒸汽温度串级控制策略研究[J].热力发电,2013,42(7):50-55.
[13]武彬,张栾英.模糊自整定PID控制在主汽温控制中的应用[J].计算机仿真,2015,32(2):387-390.
[14]韩忠旭,阎翠会,张智.锅炉蒸汽温度鲁棒控制系统研究及其稳定性分析[J].中国电机工程学报,2010,30(8):101-109.
[15]李少远.工业过程系统的预测控制[J].控制工程,2010,17(4):407-415.

