Atomistic calculations of surface and interfacial energies of Mg17Al12-Mg system

F.X.Wang,B.Li

aDepartment of Chemical and Materials Engineering,University of Nevada,Reno,NV 89557,USA

bNevada Institute for Sustainability,University of Nevada,Reno,NV 89557,USA

Abstract It is well known that precipitation hardening in magnesium(Mg)alloys is far less effective than in aluminum alloys.Thus,it is important to understand the surface and interfacial structure and energetics between precipitates and matrix.In upscale modeling of magnesium alloys,these energy data are of great significance.In this work,we calculated the surface and interfacial energies of Mg17Al12-Mg system by carefully selecting the surface or interface termination,using atomistic simulations.The results show that,the higher fraction of Mg atoms on the surface,the lower the surface energy of Mg17Al12.The interfacial energy of Mg/Mg17Al12was calculated in which the Burgers orientation relationship(OR)was satis fi ed.It was found that the(011)P|(0002)Mginterface has the lowest interfacial energy(248 mJ/m2).Because the Burgers OR breaks when{10¯12}twin occurs,which reorients the matrix,the interfacial energy for Mg17Al12and a{10¯12}twin was also calculated.The results show that after twinning,the lowest interfacial energy increases by 244 mJ/m2,and the interface becomes highly incoherent due to the change in orientation relationship between Mg17Al12and the matrix.

Keywords:Mg17Al12;Surface energy;Interfacial energy;Atomistic simulation.

1.Introduction

In recent years,magnesium(Mg)and its alloys have received significant attention due to their low densities and high specific strength.These properties make Mg alloys attractive for structural applications where improved fuel efficiency is needed[1-4].Mg-Al alloys are the most common commercial Mg alloys,and have been used as model alloys for fundamental research on deformation mechanisms and mechanical behavior.The β-phase(Mg17Al12)is the primary equilibrium precipitates which act as strengthening phase for Mg alloys.Generally,Mg17Al12precipitates increase the strength of Mg alloys by interacting with dislocation motion[5-7].Discontinuous precipitation of Mg17Al12may take place along high angle grain boundaries and grow into a cellular morphology[8,9].In contrast,continuous precipitation occurs inside the matrix of individual grains by forming large plates parallel to the basal plane of the matrix[10].Continuous precipitates follow the Burgers orientation relationship(OR)with respective to the matrix:(0001)Mg||(011)P,[2¯ī10]Mg||[ī11]P[8,11-14].

The effect of Mg17Al12on mechanical behavior of Mg alloys has been studied by a number of researchers.Robson et al.[15]calculated the hardening effect based on Orowan’s mechanism in terms of precipitate shape and habit plane.Their results suggested that the plate-like precipitates parallel to the basal plane are ineffective to impede basal slip;however,they may hinder twin growth,because precipitates inside a twin can provide a back-stress that prevents the plastic relaxation.This calculation was based on interaction between precipitates and “twinning dislocations”that can only glide on the{10¯12}twinning plane.Such interaction was questioned by recent works that have suggested that{10¯12}mode is not mediated by twinning dislocations but by atomic shuffling[16].Liand Zhang showed that the twinning shear for{1012}〈10īī〉mode should be zero[16].Consequently,twinprecipitate interaction should be minimal,which explains why precipitate hardening in magnesium alloy is not as effective as alloys with cubic structures[6].Liao et al.[17,18]simulated interactions between a Mg17Al12precipitate and prismatic slip and basal slip in magnesium using atomistic simulations.Their results indicated that a basal dislocation is able to bypass the precipitate without creating a dislocation loop around the precipitate,suggesting a rather weak interaction.In contrast,a prismatic dislocation may cut through the precipitate.They also showed that the interface between the precipitate and the matrix is incoherent and the interfacial strength is weak.Mg/Mg17Al12interfaces can act as a source of crack initiation to influence the fracture behavior[19].Mg/Mg17Al12interface also significantly influences the corrosion behavior[20,21]of Mg alloys because the free corrosion potential of Mg17Al12phase is relatively more positive in a NaCl solution.

According to phase field simulation results by Han et al.[22-24],the competition between interfacial energy and elastic strain energy determines the morphology of Mg17Al12phase[7].In their simulation,anisotropic interfacial energy and interface mobility,and elastic strain energy incorporated in their phase field model,but how the energy data was obtained was not available.Hutchinson et al.[14]calculated the Mg/Mg17Al12interfacial energies,but the effect of surface termination of Mg17Al12was not considered.Xiao et al.[25]calculated the surface energies of Mg17Al12but surface termination was not considered as well.

In this work,we performed atomistic simulations to calculate the surface and interfacial energies of Mg/Mg17Al12system.Surface termination and interfacial structure were taken into consideration.Such data are of importance for further understanding the mechanical properties of Mg alloys and for upscale simulation and modeling.

2.Simulation method

We used XMD molecular dynamics(MD)simulation package to perform our calculations.The embedded atom method(EAM)[26,27]interatomic potential for Mg and Al developed by Liu et al.[28]was used.This potential has been used in extensive MD simulations of mechanical properties for Mg and Mg alloys[29-31].More recently,Wu and Curtin[32]developed a modified EAM(MEAM[33])potential for Mg,in which the stacking fault energy has a better accuracy.Ovito[34]was used for graphic visualization.

Fig.1.Schematic of calculation method for surface energies of Mg17Al12[35].A Mg17Al12precipitate was constructed.Atoms inside Box A are used for calculating the baseline energy of Al and Mg atoms,and Box B for calculating the surface energies.

The method for our calculations is schematically shown in Fig.1[35].First,we constructed a Mg17Al12crystal which has a complex structure.They system contains a total of 928,000 atoms.The dimension of the system was 42(X)×42(Y)×11(Z)nm.The X,Y and Z are along the[100],[010]and[001]directions,respectively.The temperature in the simulation was kept constant at 10 K.Free surface conditions was applied to all three dimensions.The system was relaxed for 30 ps to minimize the potential energy of the system.To calculate the surface energy, first,we select atoms inside Box A which is in the center of the system and away from the free surfaces.The average potential energy of Al and Mg atoms were calculated.These energies were used as the baseline energy for calculating the surface energy.Because the system is sufficiently large,the effect of free surfaces on the baseline energy can be neglected.Second,we selected another Box B which contains a portion of the free surface of interest[35],and the average potential energy of Al and Mg atoms inside Box B were calculated.Then the surface energy γsurcan be calculated as:

where EMgand EAlare the average potential energies per atom for Mg and Al from box A;E′Mgand E′Alare the average potential energies per atom for Mg and Al from box B;NMgand NAlare the number of Mg and Al atoms in box B;A is the area of the free surface that is contained in Box B(in the case of Fig.1,the area is on the bottom XY-surface in box B).

The calculation of the surface energies of Mg17Al12is complicated by the fact that there are many possible surface terminations or con figurations.This complication is shown in Fig.2.Thus,all the possible surface terminations should be considered in the calculation.We calculated each surface energy of different terminations by removing the outermost atoms of each surface plane layer by layer to find the lowest surface energy termination.The highest surface energy termination was obtained as well.Fig.2(a)shows the(010)surface structure with the viewing direction being[010].It can be observed that the structure presents repeating units in all three dimensions,as indicated by the yellow arrows,and this simplifies our calculations.For instance,along the Z-[001],the structure repeats itself every unit length as indicated by the yellow arrow.Similar repetition can be seen along the X-[100]direction.

Fig.2.Possible surface terminations for Mg17Al12[35].Mg atoms are in red and Al atoms in blue.(a)The(010)surface con figuration of the simulation system for Mg17Al12.(b)The structure of Mg17Al12along theand[011]directions.

In the Burgers OR,i.e.,(0001)Mg||(011)P,,the surfaces of Mg17Al12are normal to the[011],[ī11]and[2ī1],thus,the energies of these surfaces also need to be calculated.The system was reoriented to obey a Burgers OR precipitate,and the surface energies termination was determined using the above method[35].Fig.2(b)shows the structure of Mg17Al12when the viewing direction is reoriented to the[21Similarly,the repeating units along each direction can be observed.

To calculate the energies of Mg/Mg17Al12interfaces that satis fi es the Burgers OR,we constructed a big system with dimensions of 29× 29× 56 nm(∼2.25 million atoms).The system contains both the Mg matrix and the Mg17Al12precipitate,as shown in Fig.3.The temperature condition and the surface condition were same as in the surface energy calculation.They system was relaxed for 6 ps.Atoms inside Box A which is inside the Mg matrix were selected to calculate the baseline energy of the Mg atoms of the matrix.Atoms inside Box B were selected to calculate the baseline energy of Al atoms and Mg atoms of the Mg17Al12.Another Box C which comprises the Mg/Mg17Al12interface was selected to calculate the interfacial energy.The interfacial energy γintcan be calculated as:

Fig.3.The method for calculating the Mg/Mg17Al12interfacial energy[35].Box A and B were used for calculating the baseline energies of atoms in Mg matrix and Mg17Al12.Box C was used for calculating the interfacial energy.

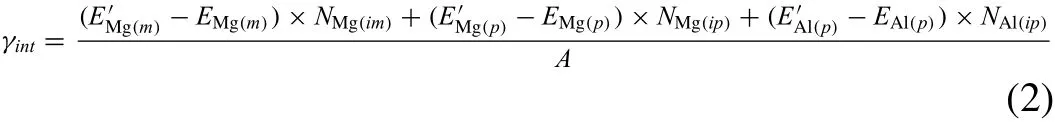
where EMg(p)and EAl(p)are the average potential energies per atom for Mg and Al in Box A;is the average potential energy per atom for Mg in Box B;andare the average potential energies per atom for Mg and Al in the precipitate in Box C;E′Mg(m)is the average potential energy per atom for Mg in the matrix in Box C;NMg(ip)and NAl(ip)are the number of Mg and Al atoms in the precipitate in box C;NMg(im)is the number of Mg from the matrix in box C;A is the area of the Mg/Mg17Al12interface contained in Box C[35].

3.Results

Fig.4.(a)The(001)surface structure of Mg17Al12with the lowest surface energy.The viewing direction is along[010].(b)The(001)surface structure with the highest surface energy[35].

Fig.5.The same surface layer may have different surface energies due to the different atomic layers underneath the surface layer.When atomic layer 1 becomes the surface,it may have either atomic layer 2(a)or atomic layer 9(b)as the underlying layer,which will give different surface energies.

As shown in Fig.2(a),the Mg17Al12β-phase presents repeating structural unit in all three dimensions.For the viewing direction of[010]in Fig.2(a),each structural unit contains twelve(001)planes or atomic layers.Therefore,we calculated the surface energies for all the twelve different surface terminations for(010).The results show that,when the 8th atomic layer was exposed as the surface termination,the surface energy is the lowest which equals 742.7 mJ/m2.The highest surface energy appears when the 10th atomic layer was exposed as the surface termination,and has a value of 980 mJ/m2.The structures with the lowest and the highest surface energy are shown in Fig.4(a)and(b),respectively.

As shown in Fig.2(a),the low index con figuration along the[100],[010]and[001]directions present centrosymmetry that simplifies our calculation of the surface energy.However,this is not the case for the[2ī1],[ī11]and[011]directions.The structure in the new orientation also shows repeating units along each direction,but only along the[011]direction the structure has centrosymmetry.Additionally,for different directions,the number of atomic layers in the repeating unit varies.The lack of centrosymmetry is demonstrated in Fig.5(a)and(b).Along the viewing direction of[2ī1],although the bottom(ī11)and the top(ī11)surface have exactly the same atomic structure,the underlying atomic layers are very different.For example,the structures of layer 2 in Fig.5(a)and layer 9 in Fig.5(b)differ significantly.Therefore,although the(ī11)surface layers in Fig.5(a)and(b)have the same atomic structure,the surface energy is expected to differ.When atomic layer 1 was exposed as the bottom(11)surface(Fig.5(a)),this termination gives a surface energy of 829 mJ/m2.In contrast,when atomic layer 1 was exposed as the top(ī11)surface(Fig.5(b)),this termination gives a surface energy of 820 mJ/m2.Our results show that due to the difference in underlying atoms,the surface energy may change by as much as 150 mJ/m2for a specific surface layer.

Table 1 Surface energies for Mg17Al12[35].

By incorporating all the possible surface con figurations,we calculated the surface energies and the results are summarized in Table 1.In terms of(11)bottom surface,the lowest surface energy appears when the 6th atomic layer becomes the bottom surface(776 mJ/m2as in Fig.6(a)).When the 9th atomic layer becomes the bottom surface,the surface energy is the highest(960 mJ/m2as in Fig.6(b)).In terms of(ī11)top surface,when the 2nd atomic layer becomes the top surface,the surface energy has the lowest value(761 mJ/m2as in Fig.6(c)).When the 3rd atomic layer becomes the top surface,the surface energy is the highest(898 mJ/m2as in Fig.6(d)).

Fig.6.(a)Bottom(1)surface that has the lowest surface energy.(b)Bottom(ī11)surface that has the highest surface energy.(c)Top(1)surface that has the lowest surface energy.(d)Top()surface that has the highest surface energy.[35](e)Bottom(011)surface that has the lowest surface energy.(f)Bottom(011)surface that has the highest surface energy.

For(011)surface,only the energies from removing atomic layer in one direction is shown because of the symmetry.Fig.6(e)shows the(011)bottom surface that has the lowest surface energy(716 mJ/m2),and Fig.6(f)shows the(011)bottom surface which has the highest surface energy(1009 mJ/m2).

The interfacial energies were calculated based on the Burgers OR.The effect of(1)surface termination of Mg17Al12on the interfacial energy was examined and the results are summarized in Table 2,which shows the interfacial energies when different atomic layers become the free surface layer(both top and bottom)of the precipitate.We also calculated the interfacial energies of different(1)terminations after〉twinning which reorients the Mg matrix,and the results are shown in Table 2 as well.Fig.7(a)shows one of the initial interface con figurations(i.e.,before relaxation)in which a(ī11)plane of the Mg17Al12was bonded to a(2¯ī10)plane of the Mg matrix.After relaxation,thetwo phases bonded together,and the interface becomes rather incoherent,as shown in Fig.7(b).

Table 2 Effect of(1)surface termination on the Interfacial energy.

Table 2 Effect of(1)surface termination on the Interfacial energy.

Bottom,[ī11]Top,[111]Number of atomic layer Matrix Twin Number of atomic layer Matrix Twin 6 449 425 2 441 462 7 447 421 1 443 451 8 426 409 9 445 438 9 407 424 8 423 427 1 444 453 7 426 446 2 430 423 6 428 439 3 424 418 5 426 429 4 454 459 4 444 436 5 440 440 3 433 417

Fig.7.(a)The initial structure before relaxation when a(1)surface of the Mg17Al12was bonded to a(2)plane of the Mg matrix.(b)The interfacial structure after relaxation,which is rather incoherent.

Table 3 Interfacial energies for Mg/Mg17Al12and Mgtwin/Mg17Al12.

From the results in Table 2,it can be observed that the change in surface termination of Mg17Al12does not alter the interfacial energy significantly.Thus,the interfacial energy is relatively insensitive to surface termination of the precipitate.Therefore,for other interfaces,to reduce the amount of calculation,we used the lowest and highest surface energy terminations of the Mg17Al12to calculate the interfacial energies.So,except for(011)P|(0002)Mginterface,each interface has two data points.The results are shown in Table 3.Fig.8(a)shows the initial structure(i.e.,before relaxation)when a(011)plane of the Mg17Al12was bonded to a(0002)plane of the Mg matrix.After relaxation(Fig.8(b)),it can be seen that the interface retains a good registry with minimal distortion to the lattice at the vicinity of the interface.

4.Analysis and discussion

4.1.Surface energy of Mg17Al12

From the surface energies shown in Table 1,it can be seen that the lowest surface energy termination appears in the(011)surface which gives a value of 716 mJ/m2.This is likely due to the complex body-centered-cubic(BCC)structure of Mg17Al12in which the(011)plane is the closed packed plane and gives the low surface energy[36].Xiao et al.[25]showed in their work that the(110)surface energy of Mg17Al12β-phase is 716 mJ/m2.Thus,the agreement is very good.Additionally,Xiao et al.[25]also reported surface energies of(100)plane(806 mJ/m2)and(111)plane(790 mJ/m2)of the β-phase.It can be seen that these values fall in the range of our calculations(743-980 mJ/m2for(100)and 776-960 mJ/m2for(111)).Because no details of surface termination was provided in[25],discrepancies can be expected.Ning et al.[37]performed density functional theory(DFT)calculation for the surface energy of(001)plane of Mg17Al12,and the value is 799 mJ/m2.From the(001)surface structure used for the surface energy calculations in[25,37],we can see that the surface termination in these calculations is identical to our case in which the atomic layer 1 is the surface(Fig.2(a)),and our result is 783 mJ/m2.Again,the agreement is satisfactory.

Fig.8.(a)The initial structure before relaxation when a(011)surface of the Mg17Al12was bonded to a(0002)basal plane of the Mg matrix.(b)The interfacial structure after relaxation,which retains a good registry and minimal lattice distortion.

Our results in Table 2 also show that,when centrosymmetry is absent,the surface energy also relies on the subsurface atoms next to the surface atoms.For example,for the(11)surface of Mg17Al12,the thickness of the atomic layers 6-9 is about 0.026 nm(Fig.2(b)).These atoms can be considered as on the same surface that has the highest atomic density.This surface termination gives lowest surface energy for the bottom(1)plane(Fig.6(a)).However,when these atoms become the top(11)surface,the surface energy is not the lowest due to the different subsurface atomic layers.Actually,the surface with the lowest energy is when the atomic layer 2 becomes the top(11)surface(Fig.6(c)).

Fig.9.Because{〉reorients the Mg matrix,after twinning,the original(011)P|(0002)Mginterface in Fig.8 now becomes(011)P|(00)Mg interface.(a)Before relaxation.(b)After relaxation.The interfacial structure and energy significantly change.

Furthermore,Figs.4(b)and 6(b),(d),and(f)show that the high surface energy terminations contain more Al atoms.This can be understood from the difference in potential energy of Al atoms(∼0.0274 eV/atom)and Mg atoms(∼0.0198 eV/atom).Therefore,the number of Al atoms becomes a more significant factor contributing to the surface energy.In contrast,surfaces with a higher fraction of magnesium atoms generate lower surface energies.

4.2.Interfacial energy of Mg/Mg17Al12

The interfacial energies for Mg/Mg17Al12in Table 3 clearly show that,in the Burgers OR,(011)P|(0002)Mgtype of interfaces gives the lowest interfacial energy(248 mJ/m2).In the work by Han et al.[38],the estimated interfacial energy value falls in the range of 140-390 mJ/m2.In the thermodynamics calculations by Hutchinson et al.[14],the interfacial energy was shown as 430 mJ/m2,which is close to the values of other types of interfaces,e.g.,(2ī1)P|(0¯110)Mgand(11)P|(20)Mg.Thus,our calculation result is reasonable.Li et al.[39]reported an energy value of 100 mJ/m2for incoherent interfaces.This value appears to be rather low and how this value was obtained was not provided.As shown in Fig.8,after relaxation,the(011)P|(0002)Mginterface has a good registry and lattice distortion near the interface is much less severe if compared to other types of interfaces.Because the interfacial energy and the elastic strain between a precipitate and a matrix largely determine the morphology of the precipitates[7],accordingly the(011)P|(0002)Mginterface is energetically more favorable.This well explains why equilibrium Mg17Al12precipitates in Mg-Al alloys generally assume a plate-like morphology with the plate plane parallel to the basal plane of the Mg matrix.

From our results(Tables 2 and 3),it is noticeable that the interfacial energies do not change dramatically when Mg17Al12surface termination changes and after twinning reorients the Mg matrix.However,for the(011)P|(0002)Mginterface that has the lowest interfacial energy,twinning significantly changes the interfacial structure and the interfacial energy,as shown in Figs.8 and 9.After twinning,the interfacial energy for this particular interface increases by 244 mJ/m2.Interfacial energy of phase boundaries and grain boundaries is predominantly determined by the interaction of atoms that are located at the interface.Thus,the structure of the interface strongly influences the interfacial energy.In general,the more coherent of an interface,the lower the interfacial energy.For instance,coherent twin boundaries always have low interfacial energies(with one exception of{111}twin boundary in hexagonal close-packed metals in which a coherent twin boundary has a much higher energy than an incoherent twin boundary because of the strong repulsive atomic interaction in a coherent twin boundary due to the small interplanar spacing[40]).Thus,the interfacial energy is a measure of coherency of an interface.The significant increase in interfacial energy of(011)P|(0002)Mginterface after twinning may have important implications for the mechanical properties of Mg-Al alloys.

It is well known that precipitate strengthening effect in Mg-Al alloys is much less than that in Al alloys.This has been attributed to geometry factors of Mg17Al12phase[5,9].When the Mg17Al12precipitates assume plate-like morphology parallel to the basal plane,the effect of hindering basal slip,which is the easiest slip system in Mg alloys,is limited.Large spacing between the plates also reduces the strengthening effect.Efforts have been made[6,9]to modify the orientation of precipitates such that they are inclined or perpendicular to the basal plane.The improvement in strengthening is still insignificant.Thus,the Mg/Mg17Al12interfacial structure and energetics need to be considered as well.Liao et al.[18]showed in their simulations that when a basal dislocation glides in contact with a Mg17Al12precipitate,no dislocation loop was generated.Instead,the interface acts as a dislocation sink,likely due to the highly incoherent interface structure and the relatively high interfacial energy.

In fact,after{10¯12}〈10¯ī1〉twinning,the Mg17Al12plates that are originally parallel to the basal plane become perpendicular to the basal plane.However,as seen in Fig.9,after twinning,the original,low energy(011)P|(0002)Mginterface becomes a more disordered,incoherent(011)P|(0ī10)Mgwith a much higher interfacial energy.This type of interfaces may reduce the strengthening effect in terms of dislocationprecipitate interaction.Thus,to design precipitate strengthened Mg alloys,interfacial structure and energy between the precipitates and the matrix should be considered as well.

5.Conclusion

In this work,we conducted atomistic calculations of surface and interfacial energies of Mg/Mg17Al12system,by taking into account the effect of Mg17Al12surface termination.The following conclusions can be reached:

(1)The surface energy of Mg17Al12is sensitive to the surface termination.Generally,surfaces with higher fraction of magnesium atoms generate lower surface energies.

(2)The Mg/Mg17Al12interfacial energy is relatively insensitive to the surface termination of Mg17Al12.(011)P|(0002)Mginterface generates the lowest interfacial energy,and the interfacial structure has a good registry and minimal lattice distortion near the interface.This explains why equilibrium Mg17Al12phase prefers a plate-like morphology parallel to the basal plane.

(3)After twinning,the original Burgers OR breaks and the interfacial structure and energies change.The original(011)P|(0002)Mginterface that has the lowest interfacial energy now becomes(011)P|(010)Mginterface with a more incoherent structure and the interfacial energy increases by 244 mJ/m2.Such a change in interfacial structure and energy may have important implications on the mechanical behavior of Mg-Al alloys.

Acknowledgments

Bin Li gratefully thank support from the U.S.National Science Foundation(CMMI-1635088).