流形降维最小二乘回归子空间分割

林智鹏，黄増裕，简彩仁

(厦门大学嘉庚学院，福建 漳州 363105)

0　引言

模式识别研究的核心问题是识别，主要包括数据的分类与聚类。本文借鉴子空间分割方法对高维小样本数据进行聚类，其主要思路是将数据分割成不同的子空间进而实现聚类。子空间分割方法可以粗略地分为迭代法、代数法、谱聚类法和统计法[1]。作为一种重要的聚类工具，子空间分割方法应用于运动对象的分割、人脸识别及图像分割等。常见的子空间分割方法包括稀疏表示子空间分割、最小二乘回归子空间分割、低秩表示子空间分割以及它们的扩展模型[1-4]。上述方法都是基于表示理论构造样本相似矩阵，然后应用谱聚类方法对数据进行聚类。

直接对高维数据进行研究不仅使得传统的模式识别方法难以适应，还会造成内存开销问题，因此研究数据降维具有重要的意义。降维手段主要包括特征选择和特征提取。特征选择的主要思路是：从特征中选出对识别有利的特征；而特征提取是对原始数据通过数学方法将其变换到不同的空间，是特征重构的一种方法。降维方法一直是模式识别的热点问题，本文研究特征提取的降维技术，特征提取的降维方法主要分为非线性降维方法和线性降维方法，主成分分析是线性降维算法的典型代表，非线性降维算法的优秀代表是流形降维，它是一种全局的降维算法，其代表有局部保持投影[5]等。

现有的子空间分割方法对高维小样本数据进行聚类时，会受到样本非线性、高维数等特点的影响，难以达到理想效果。本文提出流形学习降维子空间分割方法对最小二乘回归子空间分割方法进行研究以提高聚类准确率。该方法利用局部保持投影降维方法将样本数据变换到新的低维空间后再实行最小二乘回归子空间分割实现聚类。

1　子空间分割方法概述

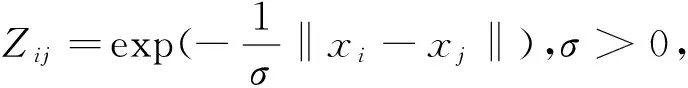
基于最小二乘回归子空间分割方法最小化Z的F-范数:

最小二乘回归子空间分割方法具有较强的鲁棒性和良好的聚类性能，可以得到解析解，因此可以快速得到表示系数：

Z=(XTX+λI)-1XTX

由上式可以计算得到仿射矩阵：

最后利用标准化分割方法[6]即可完成数据的聚类。

2　流形降维最小二乘回归子空间分割法

由于基因表达数据和图像数据等高维小样本数据具有高维数、多噪声和非线性等特点，在原有的高维空间对这类数据进行识别研究，基于线性理论的子空间分割方法难以适应，因此有必要对原始高维样本空间做变换得到低维的样本数据。本文提出利用局部保持投影降维方法将样本数据变换到新的低维空间后再实行最小二乘回归子空间分割实现聚类。

2.1　局部保持投影降维

局部保持投影[5]是一种非线性的降维方法，该方法在原有数据结构空间中保持局部流形结构，是一种基于谱图理论的学习方法。局部保持投影利用k近邻关系构造样本的权图。对数据集X∈Rm×n，有n个样本和m个特征，其相似矩阵W定义为：

其中，Nk(xi)是xi的k个近邻样本构成的集合。通过简单的代数运算可以得到局部保持投影的目标函数：

s.t.VTXDXTV=1

2.2　流形降维最小二乘回归子空间分割算法

流形降维最小二乘回归子空间分割方法利用局部保持投影降维方法将样本数据变换到新的低维空间后再实行最小二乘回归子空间分割。首先利用局部保持投影降维方法，将原始样本X变换到新的低维空间得到低维样本Xnew，接着对低维样本Xnew实行最小二乘回归子空间分割得到表示系数Z*，从而得到仿射矩阵(|Z*|+|Z*T|)/2，最后应用标准分割方法将数据分成k个子空间。算法描述如下：

算法：流形降维最小二乘回归子空间分割算法(LPP-LSR)

输入：数据矩阵X，类数k，正则参数λ

输出：k个类簇

(1)通过局部保持投影对数据X降维得到新的数据集Xnew；

(2)利用对Xnew实行最小二乘回归子空间分割方法求表示系数Z；

(3)计算仿射矩阵 (|Z*|+|Z*T|)/2；

(4)应用标准分割方法将数据分成k个子空间。

3　实验分析

本节通过实验验证流形降维最小二乘回归子空间分割法(LPP-LSR)的有效性，对比方法有最小二乘回归子空间分割法(LSR)、主成分分析降维与最小二乘回归子空间分割法结合的方法(PCA-LSR)、局部保持投影与K均值聚类结合的方法(LPP-Kmeans)，从多个角度分析本文提出方法的有效性。实验环境为Windows 7系统，内存为2 GB，所有的方法都是用MATLAB R2011b编程实现。

3.1　数据描述

选用6个公开的常用生物数据集ALLAML、Carcinom、GLIOMA、nci9、Lung_discrete、Prostate_GE和2个人脸图像数据集ORL、Orlraws10P作为实验研究对象，数据来源于http://featureselection.asu.edu/datasets.php，其主要信息如表1所示。

表1　数据集描述

所有数据集都标准化为具有单位L2范数，即用以下公式标准化:

其中，x表示一个样本。

3.2　实验结果与分析

采用聚类准确率(ACC)来评价实验结果。对于原有数据集，使用ri和si分别代表聚类算法得到的类标签和本身自带的类标签，则该准确率的计算公式[7]为：

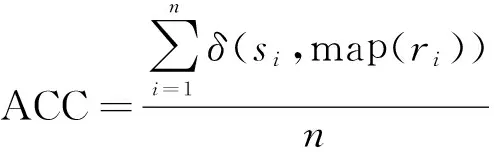
其中，n为样本总数；δ(x,y)是一个函数，当x=y时，值为1，否则为0；map(ri)是一个置换函数，其将每一个类标签ri映射成与样本自带的类标签等价的类标签。

实验的主要参数设置为主成分分析(PCA)保留比率90%，子空间分割方法的正则参数λ设为0.01，降维维数设为{20,40,60,80,100,120}。

图1给出不同的对比方法在8个数据集上的聚类准确率，可以看出，本文提出的流形降维最小二乘回归子空间分割法(LPP-LSR)可以有效地改进最小二乘回归子空间分割方法的聚类准确率。从图1中各种不同方法在不同的降维维数下聚类准确率的变化关系，可以发现除了在Carcinom和Prostate_GE数据集上，流形降维最小二乘回归子空间分割法(LPP-LSR)具有明显的优势。

图1　不同方法的聚类准确率

为更准确地反映本文方法的有效性，表2给出了各种不同方法的平均聚类准确率。从表2 不难看出，除了在Carcinom和Prostate_GE数据集上，都反映出流形降维子空间分割方法大幅度地提高了最小二乘回归子空间分割方法的聚类准确率。通过与最小二乘回归子空间分割方法(LSR)对比(表2的第一列和第二列)，可以发现利用局部保持投影降维可以有效去除噪声，提高聚类准确率。通过与主成分分析降维与最小二乘回归子空间分割法结合的方法(PCA-LSR)对比(表2的第一列和第三列)，反映出流形降维方法比传统的线性降维更适合高维小样本数据的聚类。通过与局部保持投影与K均值聚类结合的方法(LPP-Kmeans)对比(表2的第一列和最后一列)，发现最小二

乘回归子空间分割方法比传统的K均值聚类方法具有明显的优势。从不同的角度进行对比分析，发现流形降维子空间分割方法(LPP-LSR)可以得到较好的聚类准确率。

表2　平均聚类准确率　(%)

4　结论

流形降维最小二乘回归子空间分割方法主要是结合流形降维方法中的局部保持投影和最小二乘回归子空间分割法，此措施不仅改进了传统方法不利于高维数、小样本、多噪声、干扰大的非线性数据降维的缺点，还能在数据的分割聚类上取得更加突出的准确性，反映出该方法的有效性。但是该方法存在时间开销大等不足，这是今后研究的方向。

[1] LU C Y, MIN H, ZHAO Z Q, et al. Robust and efficient subspace segmentation via least squares regression[C]. Proceedings of the 12th European Conference on Computer Vision, Firenze, Italy, 2012: 347-360.

[2] ELAMIFAR E, VIDAL R. Sparse subspace clustering [C]. Proceedings of 23rd IEEE Conference on Computer Vision and Pattern Recognition, Bonn, Germany, 2009: 2790-2797.

[3] LIU G, LIN Z, YU Y. Robust subspace segmentation by low-rank representation[C]. Proceedings of the 27th International Conference on Machine Learning, Haifa, Israel, 2010: 663-670.

[4] 简彩仁,吕书龙. 权自适应最小二乘回归子空间分割法[J]. 微型机与应用, 2017, 36(10):54-57.

[5] HE X,NIYOGI P.Locality Preserving Projections (LPP)[J].Advances in Neural Information Processing Systems,2002,16(1):186-197.

[6] SHI J, MALIK J. Normalized cuts and image segmentation [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000, 22(8): 888-905.

[7] CAI D, HE X, WU X, et al. Non-negative matrix factorization on manifold[C]. Proceedings of the 8th IEEE International Conference on Data Mining, Pisa, Italy, 2008: 63-72.