基于距离变换的PRM路径规划算法

李　敏，周远远，黄　鲁

(1. 中国科学技术大学 电子科学与技术系，安徽 合肥 230027；

0　引言

随着机器人的快速发展，作为机器人关键技术之一的运动规划得到广泛的关注和研究，以概率路图法 (Probabilistic RoadMap, PRM) 和快速随机生成树 (Rapidly exploring Random Trees, RRT)为代表的基于采样的路径规划技术在实践中表现出较好的性能，同时这些算法也拥有理论上的概率完备性[1]。

在构型空间中直接计算路径被证明是非常困难的，尤其是在高维空间中[2]。PRM算法在自由空间中获取采样点，并通过采样点之间的互联来构建无向图，用于近似表示自由空间，这种方法将连续空间中的规划问题转化到拓扑空间中解决，大大减小了计算可行路径的复杂性，因此自PRM算法提出以来，受到了广泛关注并且在实际应用中取得较好的效果[3]。

尽管PRM算法在路径规划领域尤其是高维路径规划上取得了巨大的成功，但是当工作空间中存在窄通道(narrow passage)时，由于采用均匀采样，最终获得的采样点大部分会处于开阔的自由空间中，而在窄通道内的采样点相对较少(甚至没有)，这样就会造成构建的概率路图在窄通道处失去连接性，进而会造成路径规划失败[4]。

为解决PRM算法在窄通道区域的困难，许多文献提出了多种改进PRM算法。文献[4]采用增大窄通道区域的方法来增加窄通道内的采样点数目；文献[5]提出的OBPRM(Obstacle-based PRM)方法通过增加在障碍物边界处的采样点来改善PRM性能；文献[6-7]采取高斯采样策略增大在障碍物边界处的采样点密度；文献[8-9]采用桥测法，通过RBB(Randomized Bridge Builder)采样策略提高在窄通道区域的采样点密度；文献[10]结合PRM和胞元分解(Cell Decomposition)提出了一种非均匀采样策略用于解决窄通道问题；文献[11]通过引入人工势场，对落在威胁体内的点施加势场力，使之移动到自由空间内，增加窄通道内的节点数量；文献[12]提出了一种基于随机游走策略(Random Walk Strategy, RWS)的改进PRM算法；文献[13]在RBB采样策略的基础上提出了一种RSB(Randomized Star Builder)采样策略。

不同于以上方法，本文采用一种新的思路来解决窄通道问题。首先通过距离变换从原始地图中得到距离变换地图；然后利用距离变换地图来计算工作空间中障碍物稠密度，进而自适应计算不同环境下需要的采样点数目；最后用距离变换地图识别自由空间中的窄通道区域、开阔区域和边缘角落区域，在不同区域内采用不同密度的采样方法，使得采样点合理分布,构建能够通过窄通道的无向图。

1　基本PRM算法

基本的PRM算法包含两个阶段：学习阶段和查询阶段[2]。在学习阶段，PRM算法在自由空间中进行采样获取采样点，然后互联这些采样点构成代表自由空间的概率路图；在查询阶段，首先将起始构型和目标构型连接到概率路图中合适的节点，然后利用基于图的路径规划算法(D，A*，D*等)完成从起始构型到目标构型的路径搜索。对于一个环境已知的工作空间，学习阶段只需要离线执行一次即可，之后查询阶段便可以高效地在线执行。

1.1　学习阶段

学习阶段是PRM算法的关键步骤，算法流程如算法1所示[2]：

算法1：PRM(Learning Phase)

1.V←φ;E←φ;

2.fori=0,…,ndo

3.xrand← SampleFreei;

4.U ← Near(G(V, E), xrand, r);

5.V ← V ∪ {xrand};

7.ifxrandand u are not in the same connected

component of G(V, E)then

8. E←E∪{(xrand, u), (u, xrand)};

9.returnG(V, E);

其主要内容包括：

(1) 初始化。G(V,E)为一个无向图，初始状态为空。G(V,E)的顶点对应自由构型，连接顶点的边对应两个自由构型之间的无碰撞路径。

(2) 采样(SampFree)：从自由空间Cfree中采样得到自由构型xi，加入到顶点集V中进行顶点扩展。不同的采样策略将直接影响最后采样点的密度分布，原始的PRM[1]采用均匀随机采样。

(3) 邻接点计算(Near)：在空间C中定义一个距离度量ρ:C×C→。存在于顶点集V中的顶点ni，如果按照距离度量ρ为小距离(比设定的距离r小)，则将ni选择为构型xi邻域的一部分。假设构型xi的邻接点集合为Nc={n1,n2,…,nk|ni∈V,ρ(ni,xi) ≤r}，利用局部规划器尝试连接xi与其邻接点ni，对G(V,E)进行边扩展，完成图中节点之间的互联。

(4) 局部规划(Local Planner)：给定自由空间中两个自由构型x1,x2∈Cfree，局部规划器生成一条(x1,x2)之间的无碰撞路径，局部规划器需要在单次计算速度和路径质量之间进行折中。最简单的局部规划器就是生成(x1,x2)之间的直线段，这种局部规划器生成的路径简单且单次计算量代价小，应用广泛。同时为了节省空间，学习阶段不保存路径，因此局部规划器还会在查询阶段被使用。

(5)碰撞检测(Collision Checker)：给定两个构型x1,x2∈C，若连接x1和x2的直线全部位于自由空间Cfree中，即[x1,x2]∈Cfree，则x1,x2∈C为一组无碰撞的构型对。

1.2　查询阶段

借助在学习阶段构建的概率路图G(V,E)就能完成很高效的路径规划。具体方法如下。

尝试将起始构型xI和目标构型xG通过可行路径连接到G(V,E)中，若失败则无可行解，若成功则在新的无向图中利用图搜索算法得到由起始构型xI到目标构型xG的可行解。

查询阶段的关键在于如何将起始构型xI和目标构型xG连接到G(V,E)中，即寻找起始构型xI和目标构型xG到G(V,E)的可行路径。一个最简单的策略是借助与学习阶段一样的局部规划器尝试遍历连接xI与G(V,E)，同时为了限制图的规模，减小查询复杂度，文献[1]还对最大路径长度进行了限制，即超过最大长度的边将被抛弃。

2　合理的采样点分布

解决窄通道问题最直接的方法是改变采样策略，使采样点分布满足合理的分布特征[6，13-14]。

自由空间被分为三类：窄通道区域、开阔区域和边缘角落区域，不同区域的示意如图1所示。在窄通道区域，采样点少是造成概率路图连通性差的主要原因；在开阔区域，过多的采样点会影响路径查询的效率。因此合理的采样点分布应该如下：窄通道区域密集分布，开阔区域稀疏分布，边缘和角落区域中等密度分布。

3　基于距离变换的PRM路径规划

使用距离变换将原始地图中每个点的值变换为该点到距其最近障碍物的距离，这样得到的地图称为距离变换地图。距离变换地图和原始地图的对比如图1所示。经过分析，发现距离变换地图可以用来计算工作空间中的障碍物稠密度，以及识别自由空间中点所处的区域。基于距离变换地图的以上两种作用，本文提出一种新的基于距离变换的PRM路径规划算法来解决窄通道问题。距离变换有许多实现算法，本文采用文献[15]的算法得到距离变换地图，该算法被广泛采用。

图1　原始地图与距离变换地图对比

3.1　距离变换地图的作用

3.1.1计算障碍物稠密度

距离变换地图中每个点的数值代表该点到距其最近障碍物的距离(本文采用欧氏距离)，由此推测距离变换地图的平均距离值可以在一定程度上反映整个工作空间中障碍物的稠密程度。

以移动机器人所处的二维工作空间为例，工作空间尺寸为W×L，在自由空间Cfree中，num(Cfree) 表示自由空间中的总点数，d(xi) 为自由空间中某点xi对应的距离值，定义Dm为自由空间中的平均距离值，Dref为参考平均距离值(工作空间中除边界障碍物外，内部不存在障碍物时的平均距离值)。Dm计算公式如下：

参考平均距离值Dref的推导如下：

如图2所示，尺寸为W×L的矩形，将其划分为A和B两部分，A区域的点的距离值为其到上下边界的最小值；B区域可以进一步划分为8个等价的等腰直角三角形区域，每个Bi区域内点的距离值为其到外围边界的距离。

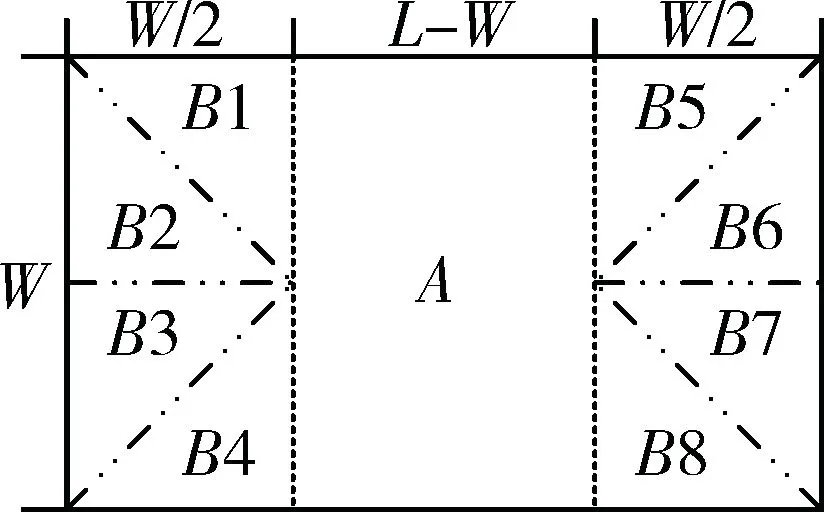
图2　无内部障碍物地图

在同一尺寸的地图中，障碍物越稠密，Dm越小。为了设计出一种适应不同尺寸工作空间的比较合理的度量方法，首先利用参考平均距离值Dref对Dm进行归一化处理，然后用1减去归一化处理后的结果，得到障碍物稠密度OD计算公式为：OD=1-Dm/Dref。

利用上式计算得到的障碍物稠密度度量OD范围为(0,1)，OD值越大表示工作空间中障碍物越稠密。

3.1.2识别不同区域

通过距离值辨别是否属于开阔区域，定义d(xi)>NarrawThreshold为开阔区域，否则为非开阔区(窄通道区域或者边缘角落区)，其中NarrawThreshold为定义的窄通道的宽度。

窄通道和边缘角落区域的区别：在窄通道区域的点，连续沿着距离值最大上升方向若干步数后，会出现局部极值点，且一直不进入开阔区域；而边缘角落区域采取这种操作时距离值则会一直增大，最终进入开阔区域。所以窄通道和边缘角落区域的区分方法为：以当前点为起点，连续向最大邻接点方向扩展NarrawThreshold-d(xi) 步，若中途出现局部极值点，则为窄通道区域，否则为边缘角落区域。

3.2　算法说明

基于距离变换的改进PRM路径规划算法包含三个步骤：

(1)计算距离变换地图。根据输入的二值地图，进行距离变换得到距离变换地图。

(2)构建PRM无向图。这一步是整个算法的核心。基于距离变换的PRM首先根据障碍物稠密度来计算所需要的采样点数目，然后在采样阶段，根据距离变换地图识别不同区域，在不同区域采取不同采样策略，使得采样点在窄通道内密集分布。

(3)路径查询。输入路径查询请求，基于步骤(2)中构建的PRM无向图，利用D算法进行路径规划，返回得到的最优路径。

距离变换地图使用3.1节中提及的方法计算，路径查询步骤与其他PRM算法一样：首先将起始点和终点连接到PRM无向图中合适的节点上，然后利用通用的D、A*等路径规划算法即可得到路径，本文的路径查询使用D算法。

PRM无向图的构建是整个PRM算法的核心部分，其构建流程如下：

算法2：DT-Based PRM

1.INIT G(V,E);

2.Init_Node = Sampling();

3.SamplingNodes.add(Init_Node)；

4.MaxNumber = getSamplingNumbers(DTMap, RobotSize);

5.while(numbers_vertex(G) < MaxNumber){

6.foreachminSamplingNodes{

7.newPts = SamplingNode(m, DTMap);

8.SamplingNodesBuffer.add(newPts);

9.Range = Range(m, DTMap);

10.neighbors = getNeightbors(G, m, Range);

11.V.add(m);

12.foreachkinneightbors {

13.if(CollisionFree(k, m))

14.E.add((k, m));

15.SamplingNodes = SamplingNodeBuffer;

16.SamplingNodeBuffer.clear()

17.

第1行， 初始化一个空的PRM无向图G(V,E)，V代表图中的节点集合，E代表图中的边集合。

第2～3行， 随机获得一个位于自由空间中的初始起点Init_Node作为采样起始点，并放入存储采样点的队列SamplingNodes中。

第5～17行，重复进行采样和局部规划操作，直到图中节点V的数目达到MaxNumber个。

第6～14行，逐个以队列SamplingNodes中的采样点为中心进行采样操作。其中：第7行，以当前采样点为起点，首先识别当前点所在的区域，然后根据不同的区域采取不同的采样策略获取新的采样点，d(xi)为xi处的距离值，MDW=M/2为安全距离。不同区域的采样策略为，在开阔区域，进行稀疏采样：分别向最大邻域和最小邻域进行d(xi)-MDW步采样，得到两个方向的采样点；在窄通道区域，进行密集采样：以当前点为中心、2·MDW～4·d(xi)为半径的环状区域内均匀采样8个点；在边缘和角落区域进行适量采样：以当前点为中心，半径为3·MWD～6·d(xi)的环状区域均匀采样4个点。第8行，将新的采样点放入另外一个队列SamplingNodesBuffer中。第9～10行，首先根据当前采样点所处区域得到需要的范围Range，然后获取G(V,E)中当前采样点的邻接点neighbors。显然如果与PRM无向图中所有的节点进行碰撞检测,计算量将非常大，考虑到算法中不同区域采样的不同采样策略，为了减小碰撞检测和局部规划的次数，在不同区域采用不同半径范围内的邻接点来完成节点间的内部互联，该范围与不同区域的采样策略有关。第11行，将当前采样点加入G(V,E)顶点集V中。第12～14行，对neighbors中所有节点与当前节点进行碰撞检测和局部规划，若存在安全路径，则添加边进入G(V,E)。第15～16行，交换SamplingNodesBuffer和SamplingNodes，准备开始下一轮迭代。

4　实验结果

为了验证算法的有效性，在不同环境下分别进行了障碍物稠密计算、区域识别以及PRM构建和路径查询仿真。

首先，设计了四种仿真环境(地图尺寸为500×500)用于测试，如图3所示。

图3　仿真环境

4.1　障碍物稠密度计算

四种环境的障碍物稠密度计算结果如表1所示，结果表明OD值能度量不同环境下障碍物稠密程度。

表1　障碍物稠密度结果

4.2　区域识别

区域识别的结果如图4所示，图中白色区域为开阔区域、斜线阴影区域为边缘角落区域、竖线网格区域为窄通道区域、黑色区域为障碍物区域。从图中可以看出，利用距离变换地图的距离值特征可有效地识别图中不同的区域。

图4　区域识别结果

4.3　采样点分布和概率路图

图5为采样点的分布示意图，图6为最终生成的PRM无向图，可以看出最终的采样点符合期望的分布，能够在窄通道区域内成功建立PRM无向图，表明本文基于距离变换的PRM路径规划算法能解决窄通道问题。

图5　采样点分布结果

图6　PRM图

表2列出了算法中的关键操作的耗时，包括：距离变换耗时、区域识别耗时、平均PRM构建耗时(10次)、路径查询平均耗时(50次)。仿真使用的机器主要参数如下：Intel(R) Core(TM) i5-4590 CPU @ 3.30 GHz，2 GB内存， 操作系统为Ubuntu 16.04。

表2　关键操作耗时　(ms)

相比于其他用于解决窄通道的PRM算法，本文提出的算法主要多了距离变换和区域识别的耗时，从表2中可以看出计算距离变换地图和区域识别的耗时相对PRM构建耗时几乎可以忽略。

5　结论

本文提出基于距离变换的PRM路径规划算法，分析了障碍物稠密度对距离均值的影响和不同区域内的距离值的分布特征，设计了一种计算工作空间中障碍物稠密度的方法，借助障碍物稠密度，算法能自适应地计算不同环境下所需采样点数目，然后利用距离分布特征来简单地识别不同区域，在不同区域采用不同的采样策略。实验结果表明，相对于其他算法，算法增加的距离计算时间代价很小，但能够根据不同环境自适应计算总采样点数目，成功解决了窄通道问题。

[1] KARAMAN S, FRAZZOLI E. Sampling-based algorithms for optimal motion planning[J]. The International Journal of Robotics Research, 2011, 30(7): 846-894.

[2] KAVRAKI L E, SVESTKA P, LATOMBE J C, et al. Probabilistic roadmaps for path planning in high-dimensional configuration spaces[J]. IEEE Transactions on Robotics and Automation, 1996, 12(4): 566-580.

[3] ELBANHAWI M, SIMIC M. SAMPLING-based robot motion planning: a review[J]. IEEE Access, 2014 (2): 56-77.

[4] HSU D, KAVRAKI L E, LATOMBE J C, et al. On finding narrow passages with probabilistic roadmap planners[C].Robotics: The Algorithmic Perspective: 1998 Workshop on the Algorithmic Foundations of Robotics, 1998: 141-154.

[5] AMATO N M, BAYAZIT O B, DALE L K. OBPRM: an obstacle-based PRM for 3D workspaces[C]. Proceedings of Third Workshop on Algorithm Foundations of Robotics (WAFR), Houston TX, 1998: 155-168.

[6] BOOR V, OVERMARS M H, VAN DER STAPPEN A F. The Gaussian sampling strategy for probabilistic roadmap planners[C].1999 IEEE International Conference on Robotics and Automation. IEEE, 1999: 1018-1023.

[7] LIN Y T. The Gaussian PRM sampling for dynamic configuration spaces[C].9th International Conference on Control, Automation, Robotics and Vision, 2006. ICARCV'06. IEEE, 2006: 1-5.

[8] HSU D, JIANG T, REIF J, et al. The bridge test for sampling narrow passages with probabilistic roadmap planners[C].2003. Proceedings. ICRA'03. IEEE International Conference on Robotics and Automation. IEEE, 2003: 4420-4426.

[9] SUN Z, HSU D, JIANG T, et al. Narrow passage sampling for probabilistic roadmap planning[J]. IEEE Transactions on Robotics, 2005, 21(6): 1105-1115.

[10] VAN DEN BERG J P, OVERMARS M H. Using workspace information as a guide to non-uniform sampling in probabilistic roadmap planners[J]. The International Journal of Robotics Research, 2005, 24(12): 1055-1071.

[11] 刘洋, 章卫国, 李广文. 基于改进 PRM 算法的路径规划研究倡[J]. 计算机应用研究, 2012, 29(1): 104-106, 139.

[12] BERA T, BHAT M S, GHOSE D. An efficient random walk strategy for sampling based robot motion planners[C].13th FIRA Robot World Congress, 2010: 234-241.

[13] ZHONG J, SU J. Robot path planning in narrow passages based on probabilistic roadmaps[J]. International Journal of Robotics and Automation, 2013, 28(3).

[14] SICILIANO B, KHATIB O. Springer handbook of robotics[M]. Springer, 2016.

[15] FELZENSZWALB P, HUTTENLOCHER D. Distance transforms of sampled functions[R]. Cornell University, 2004.