n个流形的积流形的证明
米雅薇
(新疆师范大学 数学科学学院,新疆 乌鲁木齐 830017)
乘积流形是黎曼几何的一种重要的流形模型,关于乘积流形的子流形的研究一直是黎曼几何的一个重要研究方向.乘积流形是微分拓扑学的一个重要概念,是对两个微分流形的拓扑乘积空间上给出适当的微分构造使之成为微分流形的一般方法.积流形是由两个微分流形的笛卡儿积所生成的流形.要证明2个流形的积流形需要证明2个微分流形在积拓扑空间中满足四个条件,一是这个流形的坐标卡之集是这个流形的开覆盖,二是满足同胚映射,三是相容性,四是覆盖性.那么我们也可以证明n个微分流形在积拓扑空间中满足这四个条件,叫作这n个微分流形的积流形.
1 预备知识
定义1[2]如果拓扑空间(M,τ)满足:
(1)M是A2和T2的拓扑空间,
(2)M是局部欧式的:即对任P∈M,存在P点的开领域V和映射φ,使
φ:V→φ(V)⊆Rn
是同胚映射,则称M是n维拓扑流形,φ叫坐标映射,V叫坐标域,(V,φ)叫坐标卡.
定义2[2]n维拓扑流形M上的Ck类微分构造是M上的坐标卡之集
Φ={(Vα,φα)|α∈A(指标集)}
满足:
(2)相容性:若(Vα,φα),(Vβ,φβ)∈Φ,当Vα∩Vβ≠Ø时

与
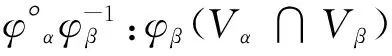
都是Ck类微分同胚.
(3)最大性:若(V,φ)与Φ中每个坐标卡是Ck相容的,则(V,φ)∈Φ.
定义3[3]n维拓扑流形M带上Ck类微分构造Φ,则称(M,Φ)是n维Ck类微分流形.
定理1[4]设(M1,Φ1)和(M2,Φ2)分别是n维和m维C微分流形,在积拓扑空间M1×M2上定义为分结构如下:
Φ={(Vα×Wβ,φα×ψ)|(Vα,φα)∈Φ1,(Wβ,ψβ)∈Φ2)}
其中对任意(v,w)∈V×W∩Vα×Wβ,有
(φα,ψβ)(v,w)Δ(φα(v),ψβ(w))
则(M1×M2,Φ)是m+n维C微分流形,称为M1和M2的积流形.
2 n个流形的积流形的证明
定理2设(M1,Φ1),(M2,Φ2),…,(Mn,Φn)分别是M1,M2,…,M3维C微分流形,在积拓扑空间M1×M2×…Mn上定义的微分构造如下:
Φ={(Vα1×Vα2×…×Vαn,φα1×φα2×…×φαn)|(Vα1,φα1)∈Φ1,(Vα2,φα2)∈Φ2,…,(Vαn,φαn)∈Φn}其中对任意(v1,v2,…,vn)∈Vα1×Vα2×…×Vαn,有
(φα1,φα2,…,φαn)(v1,v2,…,vn)Δ(φα1(v1),φα2(v2),…,φαn(vn))
则(M1×M2×…×Mn,Φ)是m1+m2+…+mn维C微分流形,称为M1,M2,…,M3的积流形.
证明:(1)因为M1,M2,…,Mn是A2,T2拓扑空间,所以积拓扑空间M1×M2×…×Mn也是A2,T2拓扑空间.
(φα1×φα2×…×φαn):Vα1×Vα2×…×Vαn→(φα1×φα2×…×φαn)(Vα1×Vα2×…×Vαn)=φα1(Vα1)×φα2(Vα2)×…×φαn(Vαn)⊂Rm1×Rm2×…×Rmn=Rm1+m2+…+mn是同胚.
因为
(φα1×φα2×…×φαn)(v1×v2×…×vn)
=(φα1(v1),φα2(v2),…,φαn(vn))
=(x1,x2,…,xn)∈φα1(Vα1)×φα2(Vα2)×…×φαn(Vαn)
并且
=(x1,x2,…,xn)
所以
即
(φα1×φα2×…×φαn)-1(x1,x2,…,x3)=
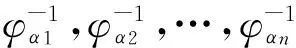
(3)覆盖性:因为
所以
(4)相容性:设

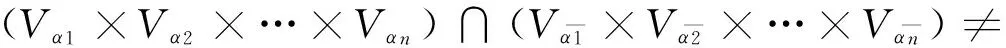
都是C映射,从而
是C映射,同理也是C映射.所以(M1×M2×…×Mn,Φ)是m1+m2+…+mn维C微分流形,称为M1,M2,…,M3的积流形.
参考文献:
[1]纪永强. 子流形几何[M].北京:科学出版社,2004.
[2]陈省身,陈维桓.微分几何讲义[M].北京:北京大学出版社,2001.
[3]伍鸿熙,沈纯理,虞言林.黎曼几何初步[M].北京:北京大学出版社,1989.
[4]陈维桓,李兴校.黎曼几何引论(上册)[M].北京:北京大学出版社,2002.
[5]白正国,沈一兵,水乃翔,等.黎曼几何初步[M].北京:高等教育出版社,2004.
[6]张丹松,刘西民.一类殆切触流形的半不变子流形[J].吉林化工学院学报,1995(2):59-63.
[7]张丹松,刘西民.K-流形的全殆切触脐半不变子流形[J].吉林化工学院学报,1995(4):66-69.
[8]肖庆丰.线性流形上广义反次对称矩阵反问题的最小二乘解[J].吉林化工学院学报,2012,29(1):78-81.
[9]刘长荣,肖庆丰.线性流形上反次对称矩阵反问题的最小二乘解[J].吉林化工学院学报,2005(4):93-95.
[10] 王佳.黎曼积流形的子流形[J].西南师范大学学报:自然科学版,1988(1):13-20.

