基于多目标PSO算法的DSP防护优化设计

,,

(西安电子科技大学 空间科学与技术学院,西安 710071)

0 概述

近年来,芯片朝着微型化、低功耗和高性能方向发展。然而在其性能得到提高的同时,微处理器的可靠性更容易受到外界环境的干扰,由此引发的软错误已不可忽视[1-3]。文献[4]通过故障注入法指出80%～90%的计算机故障由软错误所造成;文献[5]则预测软错误将以每代8%的速度增长。可见,软错误已成为阻碍计算领域发展的一个日益严峻的问题。

为消除软错误对计算机的影响,研究者提出多种针对软防护的容错方式。不同的软防护方法可以提高可靠性,但同时也会带来代价开销。文献[6]指出,三模冗余可以提高系统可靠性,但冗余所引起的代价制约了并行计算的可扩展性;文献[7]指出,冗余技术可使系统可靠性得到提高,但同时也会使资源开销比原始电路增加200%;文献[8]指出,汉明码技术通过增加冗余代码可实现抗干扰。由此可知,防护的可靠性与代价是对系统进行防护时面临的一对矛盾。现有研究多数针对某种防护方法进行改进,研究如何提高防护的可靠性,降低额外代价,较少有针对系统防护组合的研究。文献[9]提出了一种具有芯片级在线修复能力的强容错TMR系统结构及设计方法;文献[10]则针对软件测试进行研究,将测试资源合理分配给系统的不同模块,使系统可靠性和测试成本2个方面同时得到优化。

在对系统进行软防护的过程中,需要设计合适的算法提高可靠性并减少资源消耗。目前粒子群优化(Particle Swarm Optimization,PSO)算法主要针对连续空间,关于离散解的研究较少,用于求解防护模型的研究更少。例如:文献[11]是对离散粒子群算法应用背包问题的研究;文献[12-13]将离散粒子群算法应用于Web服务组合,算法复杂度较高;文献[14]提出针对连续空间的PSO算法,同时设计空间超格和变异策略以提高算法收敛速度,保证解的均匀性与广泛性。

本文以数字信号处理器(Digital Signal Processor,DSP) C6701芯片为研究对象,设计一种基于多目标PSO的DSP防护优化方法。首先对系统程序进行模块划分,然后建立以功能模块所采取防护方法构成的组合为自变量,以系统性能和代价为优化目标的系统优化模型,最后利用文献[14]算法改进粒子群速度位置公式,使其可以求解本文模型。

1 系统防护优化模型

为找到一种合适的系统防护组合优化系统防护的可靠性及防护代价,需要建立与防护方法选择有关的系统代价与性能的多目标优化模型。为此,本节首先给出系统代价与可靠性的评估方法,然后结合模块防护方案的选择建立系统防护优化模型。

1.1 系统代价和可靠性评估

根据系统模块之间的拓扑关系计算系统的代价与可靠性,具体步骤如下:

1)模块划分。根据DSP汇编指令的特点[15]和基本块的概念[16],对系统汇编代码进行功能模块划分(每个功能模块就是顺序执行的一段汇编代码),将模块编号为1～N。

2)根据模块跳转指令B跳转到的模块地址确定模块之间的拓扑关系。

3)计算模块的代价与可靠性。

(1)计算模块M(M=1,2,…,N)的代码量并做线性归一化处理,归一化后将模块M代码量记为CM。

(2)计算模块M的执行时间[17]并做线性归一化处理,归一化后将模块M执行时间记为TM。

(3)计算模块M的可靠性[18],记为RM。

4)确定执行路径。根据模块的拓扑关系,利用深度优先搜索算法求系统的执行路径,每条路径由部分功能模块组成:p表示执行路径,S表示执行路径条数。如图1所示,模块1为起始模块,模块N为终止模块,则模块1→2→5→7→N为一条包含5个模块的路径,模块1～模块N的所有路径条数即为执行路径条数。

图1 模块拓扑关系

5)计算系统代价与可靠性。

(1)计算系统代码量C。系统代码量为各个模块代码量之和:

(1)

其中,CM表示模块M的代码量。

(2)计算系统执行时间T。系统执行时间为各路径执行时间的均值,而单条路径各功能模块为级联的方式,因此,单条路径执行时间为该路径模块执行时间之和:

(2)

(3)计算系统可靠性R。系统可靠性为各路径可靠性的均值,而单条路径各模块为级联的方式,因此,单条路径可靠性为各个模块可靠性的乘积:

(3)

通常人们只会关注系统代价和可靠性。代价和可靠性为2个目标,因此,本文将各个代价的加权平均看作一种代价。系统代码量加权系数为a,系统时间量系数为b,且a+b=1,工程人员可以根据自己更看重的代价而调整加权系数。综合式(1)～式(3)可以得到以下评估系统代价、可靠性的模型:

(4)

其中,g1表示系统代价,g2表示系统可靠性。

1.2 多目标系统防护组合模型

对系统中的各个模块进行防护,可以选择的防护方法有多种,如何为系统中的各个模块选择合适的防护方法,使得防护后系统的可靠性得到提高,并且使防护后系统的代价尽可能小,成为系统防护的关键。针对该问题,本文建立系统防护的多目标优化模型,具体步骤如下:

1)根据各种模块软防护后代价和性能的变化特点,建立如下模型:

2)建立系统防护组合k=[k1,k2,…,kM,…,kN],其中,限制条件为{k|kM∈{1,2,…,Q}},kM表示标号为M的模块采用编号为kM的防护方法。

3)建立系统自变量为k的多目标优化模型,将加入防护后的各个模块替换式(4)中模块的数据,可以得到系统代价和可靠性的多目标模型。同时,为与标准多目标优化公式统一,以系统出错率为优化目标,系统出错率为1减去系统可靠性,如式(5)所示。

(5)

2 改进的粒子群优化算法

标准粒子群优化算法的设计思想是:随机初始化一群没有质量和体积的粒子,将每个粒子看作待求问题的一个解,利用适应度函数衡量粒子的优劣,所有粒子在可行解空间内按照位置速度公式更新自己的位置,追随粒子最优解,经过若干代搜索后得到该问题的最优解[19]。粒子群优化算法中粒子更新的运动方程[20]如下:

(6)

(7)

本文提出一种离散多目标粒子群优化算法,基于自适应概率选择机制进行粒子位置更新,使用粒子群优化算法求解所构建的系统防护模型,使系统防护代价和性能2个目标函数尽量达到最优。本文借用文献[14]对连续空间的粒子群优化所用的技术,其中包括内部种群用于存储所迭代粒子的当前位置和个体历史最优位置,外部种群的存储以自适应网格外部档案维护的方式来尽量使Pareto面上的解分布均匀,提高种群多样性。此外,本文对连续空间所用的位置速度公式和参数进行改进,使其可以求解所构建的离散空间模型。

2.1 内部种群

2.2 外部种群

2.3 粒子更新位置速度公式

2.3.1 参数定义

首先定义粒子自适应飞行参数λ=c1/c2以及ω。其中,c1表示粒子向个体历史最优位置变化的权重因子,c2表示粒子向全局历史最优位置变化的权重因子,ω表示粒子向一般位置(除个体历史最优及全局历史最优以外的位置)变化的权重因子。本文利用c1、c2、ω共同控制粒子位置的更新,定义公式如下:

c1+c2=1-ω

(8)

λ=c1/c2

(9)

经变形可以求得:

c1=(1-ω)-c2

(10)

(11)

模仿连续空间粒子群算法参数的设置方法,设置如下离散粒子群算法的参数:

(12)

(13)

2.3.2 轮盘赌法实现

2.3.3 粒子更新

1)定义概率权重向量RM=[r1,r2,…,ri,…,rQ],其中,ri表示kM取值为i的概率权重,即模块M的所有可用防护方法中第i种防护方法被选中的概率。

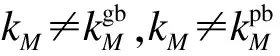
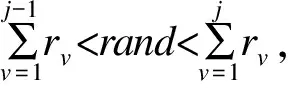
2.4 算法步骤

利用改进的粒子群优化算法求解系统防护组合模型,具体步骤如下:

1)粒子群优化算法位置编码,构建防护方法组合k。

2)粒子算法参数设置,包括粒子群算法最大进化迭代次数G、参数λ0、λG、ω0、ωG。

3)初始化内部种群POP,随机选择L个步骤1)中防护组合作为内部种群。

4)评价内部种群,根据系统防护组合优化模型,计算各个粒子2个目标函数f1(k)、f2(k)的值,并将两者组合在一起作为POP中各粒子的适应值向量,进一步根据Pareto占优准则评价内部种群POP中粒子对应的系统防护组合方法的优劣。

5)初始化外部种群REP,将内部种群中各粒子进行两两比较,并根据Pareto占优准则将内部种群中对应非劣解的所有粒子复制到外部种群REP中,完成对REP的初始化。

6)初始化内部种群中各个粒子的个体历史最优位置。将内部种群POP中的粒子依次复制到pbest中,得到POP中各个粒子的个体历史最优构成的种群pbest,完成对pbest的初始化。

7)更新内部种群。按本文粒子更新的公式进行内部种群更新。

8)重新评价内部种群。按步骤4)的方式重新评价内部种群。

9)更新外部种群。利用空间超格进行更新。

10)更新每个粒子的个体历史最优构成的种群pbest。如果内部种群POP中的某个粒子优于其在pbest中的个体历史最优粒子,则用这个粒子替换pbest中该粒子的个体历史最优粒子;否则,pbest中该粒子的个体历史最优粒子保持不变。

11)判断迭代是否到达G次,若未结束,则迭代次数加1并转步骤7);否则迭代结束,将外部种群REP中的Pareto最优解导出,作为系统防护组合的一组Pareto最优解,该解集可用于指导最终防护方法的选择。

3 实验与结果分析

为了验证本文建模与算法的可行性,分别针对多个DSP C6701的工程进行实验并对结果进行分析。实验中算法的相关参数设置为:防护方法种类Q为6,系统代价的权重系数a为0.5,b为0.5,空间超格划分数目为15,自适应飞行参数λ取值0.8～0.2,ω取值0.95～0.5,均随着进化代数线性变化,内部种群POP,外部种群REP大小均设置为60,迭代次数G设置为100。运行系统为ubuntu 16.04,64位操作系统,8 GB运行内存,编译运行软件为qt5.5.0。

3.1 系统防护实验

对在CCS上实现的DSP工程快速排序程序进行分析。该程序中有31个功能单元模块,模块编号为1～31,表1中列出了程序优化前10个模块的相关数据,分别为各个功能单元模块防护前的可靠性、代码量、时间量,从而构成建模前的原始数据。

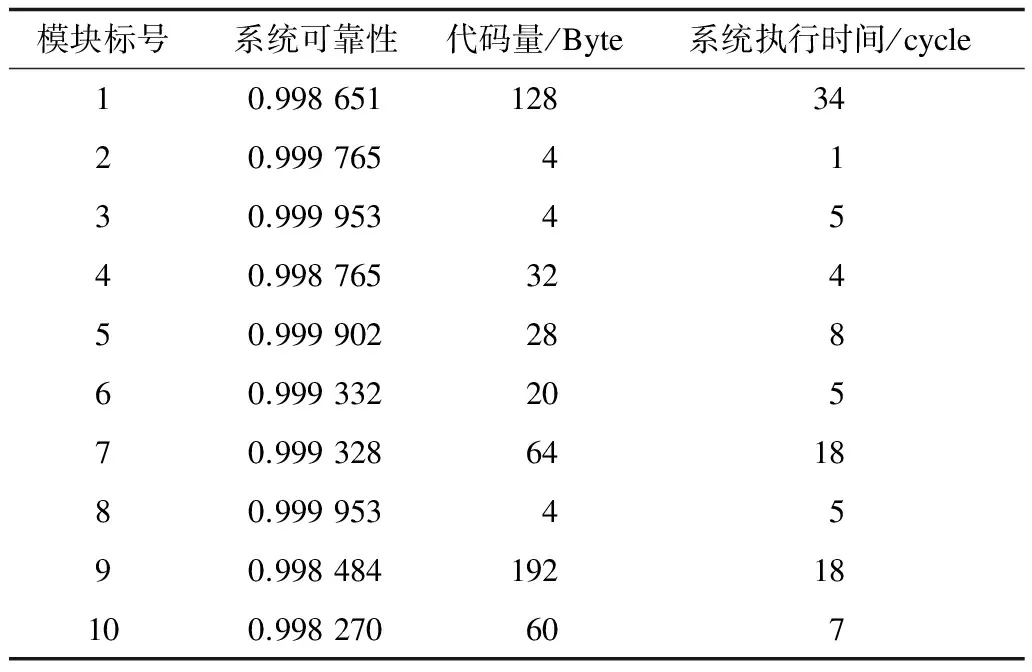
表1 快速排序功能模块相关数据

本文对上述原始数据进行系统防护,得到优化算法的实验结果以及防护组合,分别如图2、表2和表3所示。

图2 快速排序防护优化结果

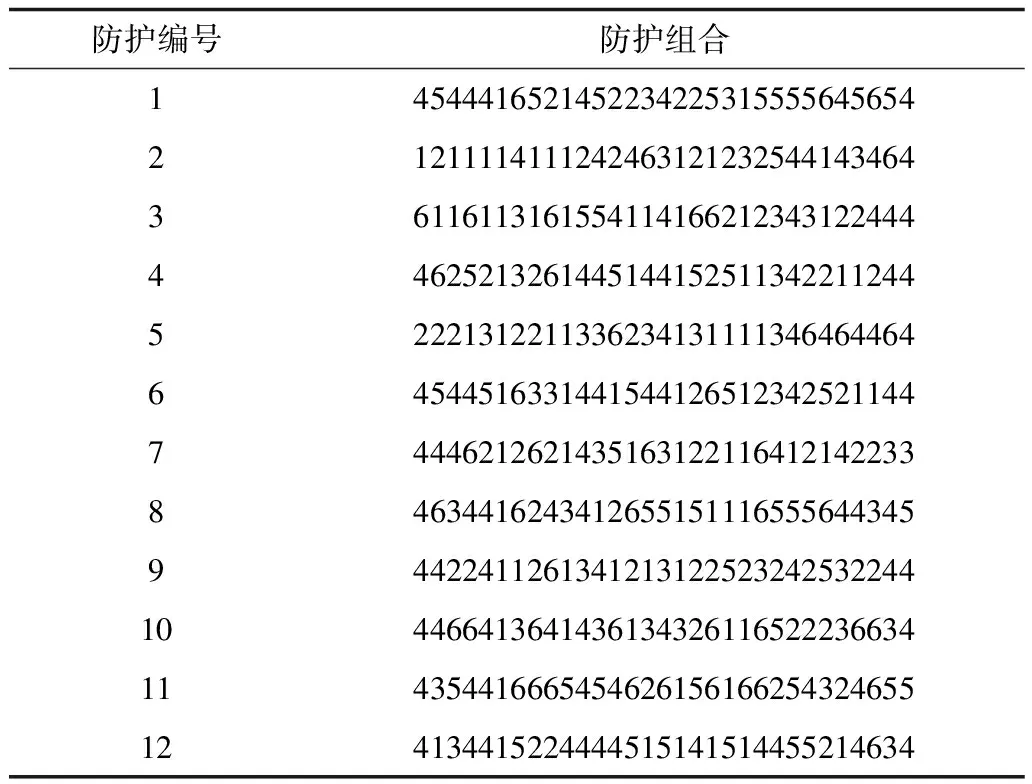
表2 快速排序工程系统防护组合

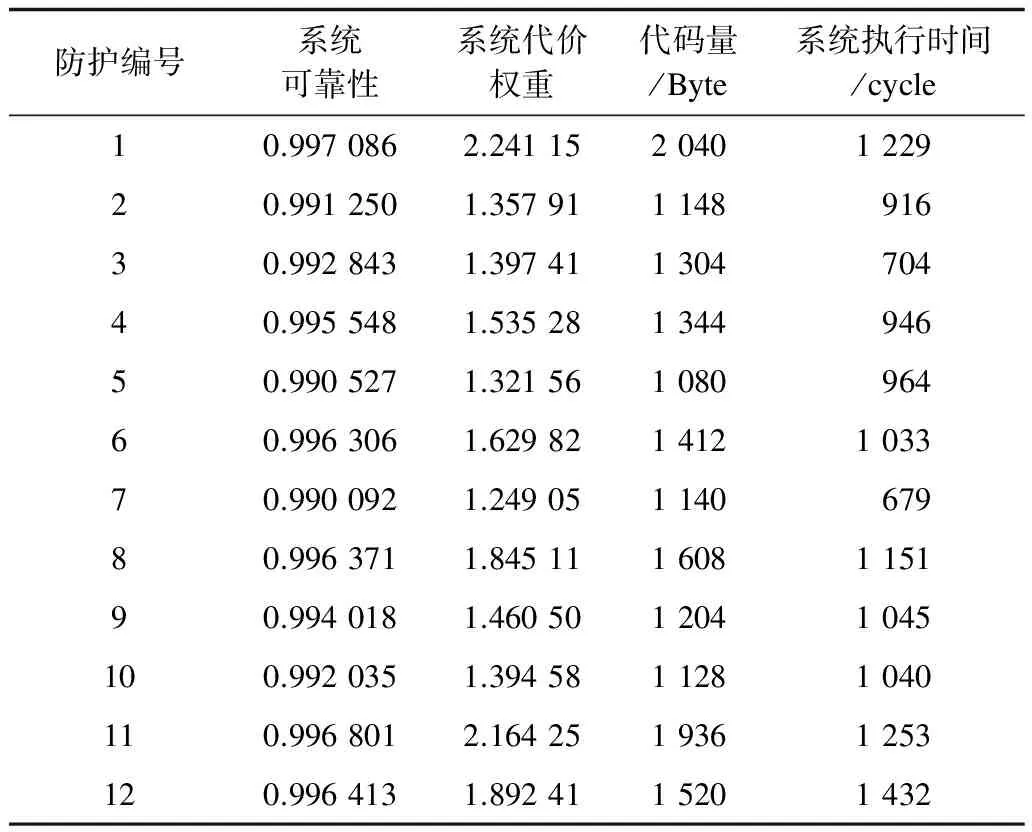
表3 快速排序工程防护后相关数据

在图2中,PF-0、PF-25、PF-50、PF-75、PF-100分别代表未进行系统防护的系统出错率,以及系统加权代价和系统防护且算法迭代次数为25代、50代、75代、100代所形成的Pareto前沿。图中每一个点对应一种防护组合,通过各个优化结果的点可以看出,不同的防护组合,都会增加系统的代价开销,降低系统的出错率。PF-100线上有12个点,代表优化到100代所得到的12种防护组合,并且系统防护效果好于其他迭代代数。

表2给出的12种系统防护组合对应图2中的PF-100线上的12种防护组合(每种防护组合中的防护方法编号1、2、3、4、5、6分别对应无防护、关键指令的三模冗余、关键变量的三模冗余、模块的时间冗余、模块的时空冗余、关键变量的汉明码这6种防护方法)。每种防护组合分别代表功能模块1～模块31所采用的防护方法,以表2中防护编号1为例,其表示对快速排序模块编号为1～31的模块依次采取防护方法编号为4、5、4、4、…、5、4对应的防护方法。

表3给出了采用表2系统防护组合所对应的数据,包括系统可靠性、系统代价加权、代码量和系统执行时间,同时对应图2中PF-100线上的12个点。

3.2 算法对比

由于粒子群优化算法一般针对连续空间,目前对于离散算法的研究较少,虽然现已存在离散版二进制粒子群优化算法BPSO[21]以及一些对该版本的改进方案用于求解组合优化问题,但是这些算法的效果并不理想,另一方面也不适用于求解本文所构建的模型。为验证本文所提粒子迭代更新公式的有效性,将对比实验算法设置如下:

实验1:应用本文设计的粒子迭代更新公式进行粒子寻优位置的更新。

实验2:不应用本文设计的粒子迭代更新公式,对粒子迭代更新的位置在可行解中随机选取。

下面分别给出针对DSP C6701程序而设计的堆排序、FFT(64位快速傅里叶变换)和一个DSP与FPGA进行通信的系统进行实验对比,以验证本文方法的可行性。

在实验对比中,堆排序的功能模块数量较少,当优化代数够大时,实验1与实验2数据都会接近Pareto最优面。从图3中可以看出,实验1数据略好于实验2。图4和图5对应的64位快速傅里叶变换和通信系统都为200个～300个功能模块数量,可以看出,改进粒子群优化算法得到的实验1数据明显好于实验2数据,另外,由于改进的粒子群优化算法需要迭代更新公式进行更新,时间会略微低于粒子更新时在可行解空间随机产生粒子进行位置更新的时间,表4给出的运行时间也验证了此结论,但是时间消耗在同一量级,影响不大。通过以上实验可以看出,本文提出的改进离散粒子群优化算法在一定程度上可以有效寻找最优解。

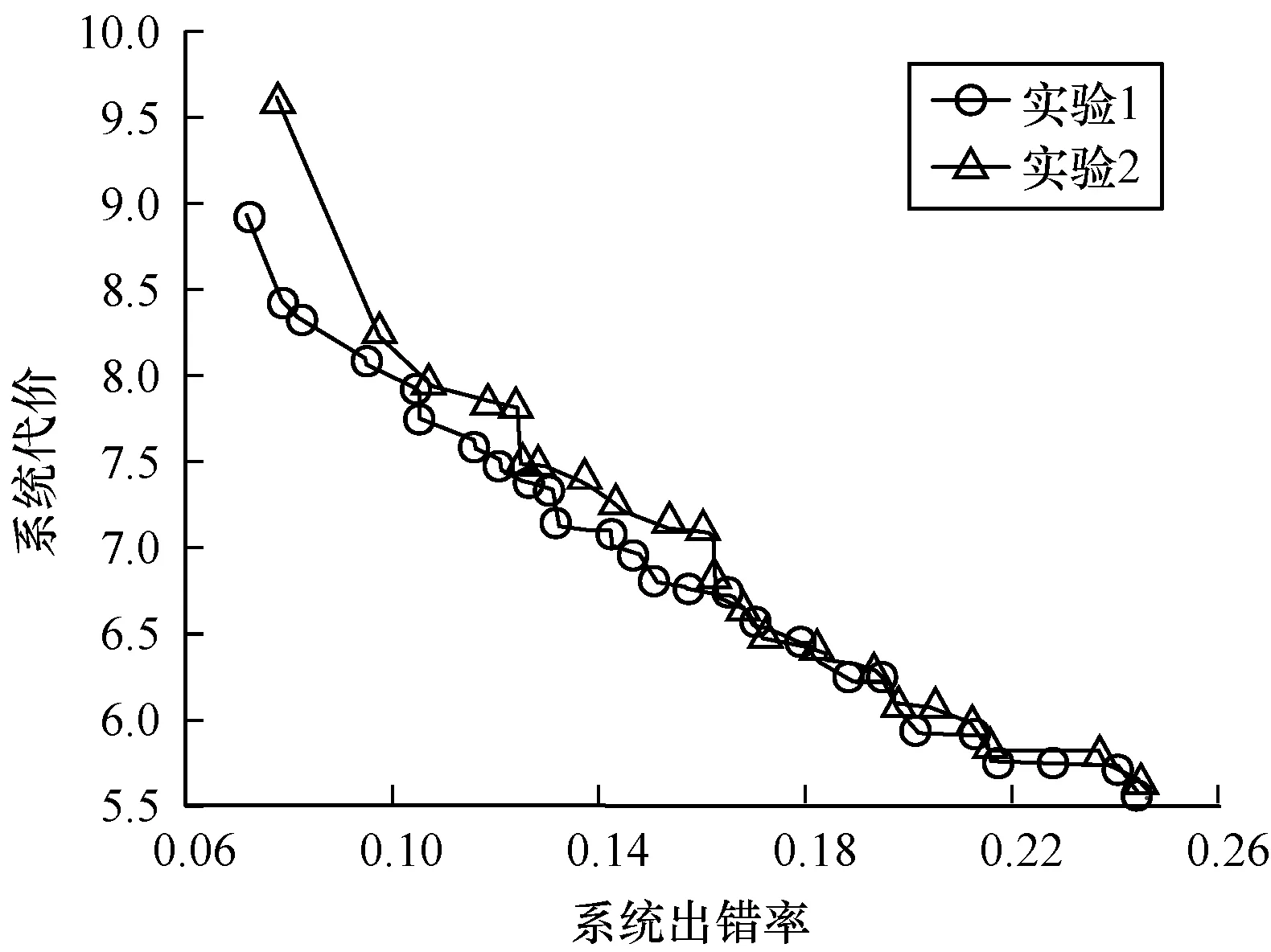
图3 堆排序工程防护优化结果

图4 FFT工程防护优化结果

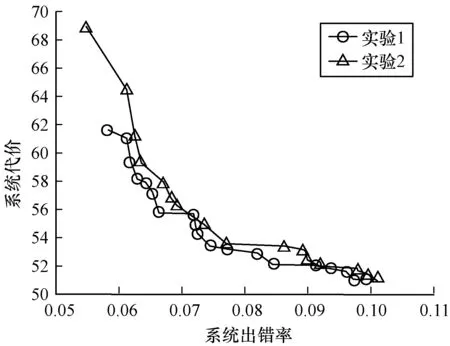
图5 通信系统工程防护优化结果

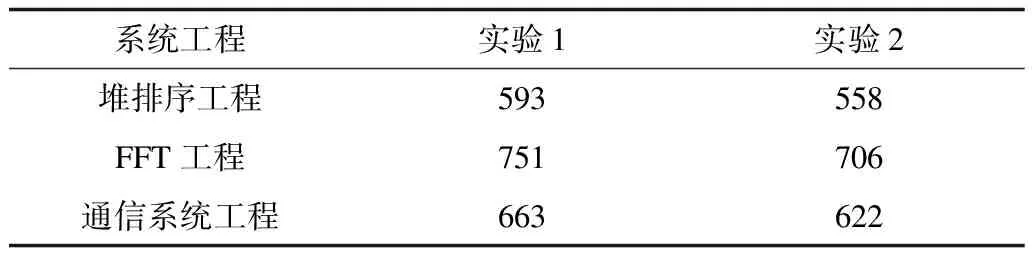
表4 实验1与实验2运行时间对比 s

4 结束语

本文针对系统软防护引起的可靠性与代价这一矛盾,设计了基于粒子群优化算法的DSP系统防护解决方案,以指导工程设计人员针对系统功能模块进行防护方法的选择。由实验结果可知,本文针对系统各个模块建立的以代价和可靠性为2个优化目标,以各个模块防护方案所组成的向量为自变量的模型,可以准确地反映出不同防护组合对应的系统代价和可靠性的关系。为求解所建模型,提出基于自适应概率选择机制的离散多目标粒子群优化算法,并通过实验对比验证了该算法的可行性与有效性。同时,从系统防护实验的分析结果也可以看出,利用本文优化方法选取的系统防护组合对系统进行防护,能够得到比较满意的系统可靠性和系统代价。

[1] BORKAR S.Designing reliable systems from unreliable components:the challenges of transistor cariability and degradation[J].IEEE Micro,2005,25(6):10-16.

[2] ZIEGLER J F.IBM experiments in soft fails in computer electronics(1978—1994)[J].IBM Journal of Research Development,1994,40(1):3-18.

[3] BAUMANN R C.Radiation-induced soft errors in advanced semiconductor technologies[J].IEEE Transactions on Device and Materials Reliability,2004,5(3):305-316.

[4] CLARK J A,PRADHAN D K.Fault:a method for validating computer system dependability[J].IEEE Computer,1995,28(6):47-56.

[5] SHIVAKUMAR P,KISTLER M,KECKLER S W,et al.Modeling the effect of technology trends on the soft error rate of combinational logic[C]//Proceedings of International Conference on Dependable Systems and Networks.Washington D.C.,USA:IEEE Press,2002:389-398.

[6] 王之元,杨学军,周 云.大规模MPI并行计算的可扩展三模冗余容错机制[J].软件学报,2012,23(4):1022-1035.

[7] 张 超,赵 伟,刘 峥.基于FPGA的三模冗余容错技术研究[J].现代电子技术,2011,34(5):167-171.

[8] 赵建武,周航慈.提高汉明码对突发干扰的纠错能力[J].单片机与嵌入式系统应用,2004,4(1):15-16.

[9] 姚 睿,王友仁,于盛林,等.具有在线修复能力的强冗余三模冗余系统设计及实验研究[J].电子学报,2010,38(1):177-183.

[10] WANG Z,TANG K,YAO X.Multi-objective approaches to optimal testing resource allocation in modular software systems[J].IEEE Transactions on Reliability,2010,59(3):563-575.

[11] 刘建芹,贺毅朝,顾茜茜.基于离散微粒群算法求解背包问题研究[J].计算机工程与设计,2007,28(13):3189-3191.

[12] 范小芹,蒋昌俊,方贤文,等.基于离散微粒群算法的动态Web服务选择[J].计算机研究与发展,2011,47(1):147-156.

[13] 于明远,朱艺华,梁荣华.基于混合微粒群算法的网格服务工作流调度[J].华中科技大学学报(自然科学版),2008,36(4):46-47.

[14] COELLO C A C,PULIDO G T,LECHUGA M S.Handling multiple objectives with particle swarm optimization[J].IEEE Transactions on Evolutionary Computation,2004,8(3):256-279.

[15] Texax Instruments.TMS320C6000 CPU and instruction set reference guide[EB/OL].(2006-07-10)[2017-02-10].http://www.ti.com/lit/ug/spru189g/spru189g.pdf.

[16] AHO V A,SETHI R,ULLMAN J D.编译原理[M].李建中,张守旭,译.北京:机械工业出版社,2008.

[17] 周国昌,郭宝龙,高 翔,等.基于分布函数的WCET快速估计[J].计算机科学,2016,43(5):157-161.

[18] 唐 柳,黄樟钦,侯义斌,等.微处理器可靠性 AVF 评估方法研究综述[J].计算机应用研究,2014,31(3):651-657.

[19] SALAZAR-LECHUGA M,ROWE J E.Particle swarm optimization and fitness sharing to solve multi-objective optimization problems[C]//Proceedings of 2005 IEEE Congress on Evolutionary Computation.Washington D.C.,USA:IEEE Press,2005:1204-1211.

[20] POLI R,KENNEDY J,BLACKWELL T.Particle swarm optimization:an overview[J].Swarm Intelligence,2007,1(1):33-57.

[21] KENNEDY J,EBERHART R C.A discrete binary version of the particle swarm algorithm[C]//Proceedings of IEEE International Conference on Systems,Man,and Cybernetics.Washington D.C.,USA:IEEE Press,1997:4104-4108.