轮对动不平衡对构架扭转变形的贡献评估
林俊,邹晓龙
(中车青岛四方机车车辆股份有限公司,山东 青岛 266111)
0 引言
随着车辆运营速度的提高,车辆激扰频率也随之提高.最为显著的当属轮对的动不平衡引起的振动.避免共振成为首要的讨论对象.轮对动不平衡频率主要体现在纵断面上质心偏移车轴中心线,绕车轴旋转一周,产生一周的激励.该激励通过一系弹簧传递到构架.车辆运营速度达到330km/h,对于半径为460 mm的车轮来说,激励达到约32 Hz.通常构架的一阶扭转频率40 Hz以上,但由于结构更改,存在降低构架扭转频率的情况,例如本文构架模型增加附加装置后扭转频率将降低到32 Hz左右,此时的动不平衡激励频率与构架扭转频率相当,存在扭转共振的风险.
目前关于动不平衡的研究主要集中在车辆舒适度方面,未涉及与构架扭转频率接近时的构架动力学性能研究.本文将构架的动力学模型由刚性体改为弹性体,建立了柔性构架与刚性车辆系统的耦合模型,研究了频率接近动不平衡频率时,构架的扭转变形和车辆的动力学情况,相关计算结果还可为疲劳计算和试验提供载荷依据,也可为整车动力学及动应力试验提供参考.
1 模型的建立
1.1 构架有限元模型
本文所建立的构架有限元模型如图1所示,模型中共有58190个单元.构架主要材料为合金钢,其弹性模量为2.1 MPa,泊松比为0.36,密度为7 800 kg/m3.有限元模型与车辆坐标系保持一致,称图1中x方向为纵向,y方向为横向,z方向为垂向.
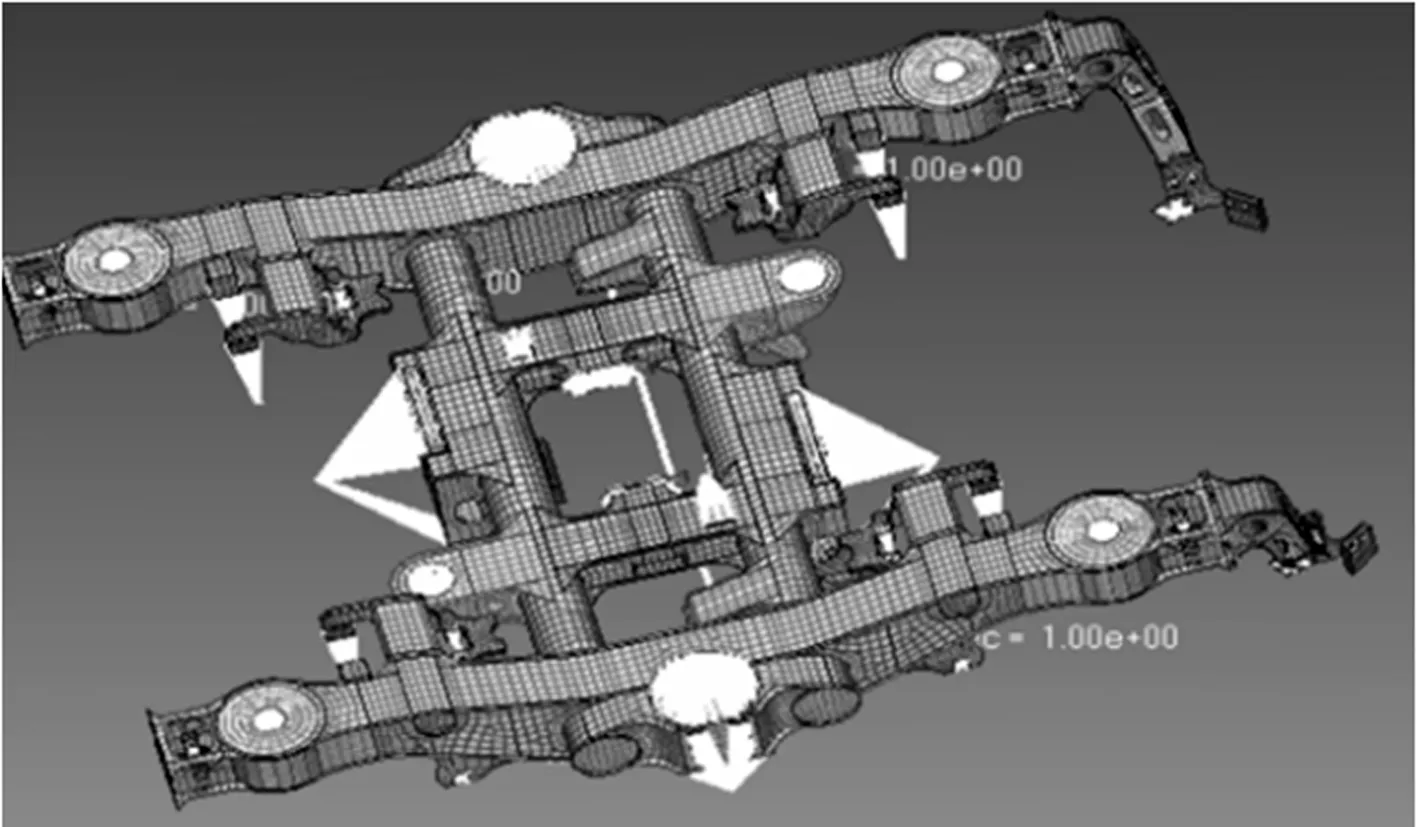
图1 构架有限元模型
为实现构架有限元模型与车辆动力学模型的耦合仿真,在有限元模型中分别在抗蛇形减振器、横向减振器、空气弹簧、一系弹簧、一系减振器、横向止挡、齿轮箱吊点处创建了主节点.
1.2 整车动力学模型
动力学模型中的车体、构架、轮对各取 6个刚体自由度,即纵向、横向、垂向、侧滚、点头、摇头 (其中轮对垂向和侧滚运动是非独立运动);轴箱体和齿轮箱取1个点头自由度(相对于轮对),牵引拉杆取3个转动自由度.整车共有58个刚体自由度.
采用Simpack多体动力学软件建立的某型高速动车组车辆如图2所示.

图2 某型车辆动力学模型
构架与轮对之间在垂向上存在一系弹簧和一系垂向减振器,构架扭转变形体现在构架在一系弹簧处的垂向变形.一系垂向减振器采用maxwell模型[1],见图3,其截止频率大于60 Hz.
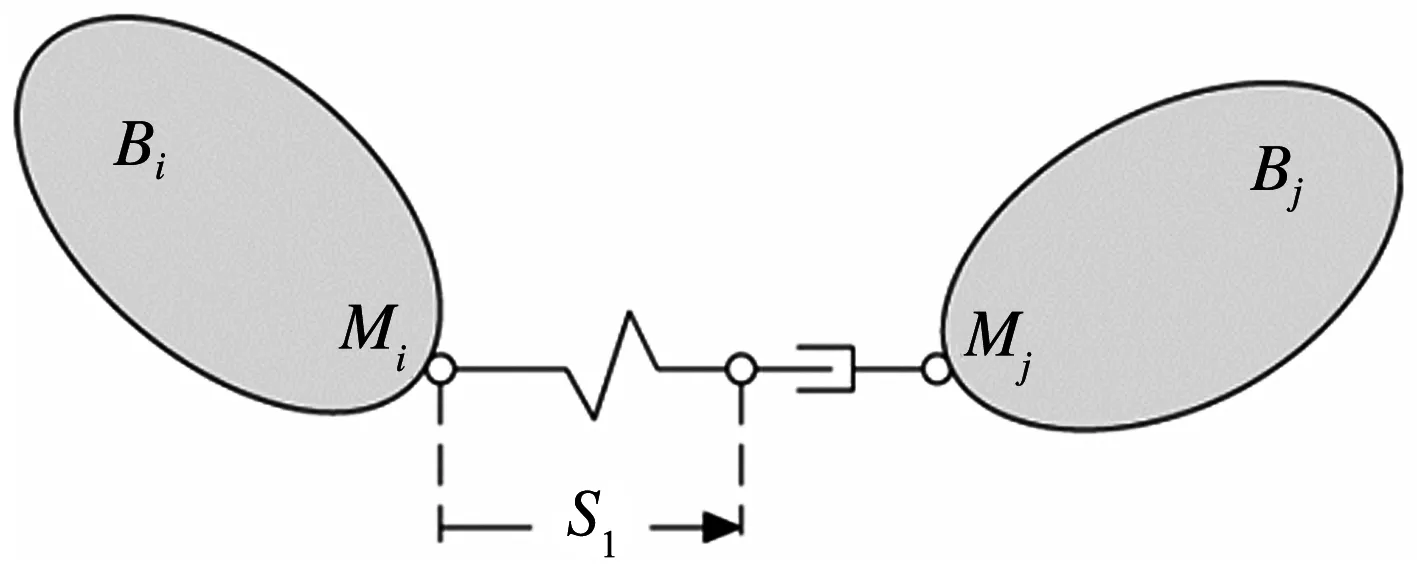
图3 一系垂向减振器Maxwell动力学模型
1.3 构架一阶扭转振型与固有频率
在动力学计算过程中,构架上的任意一点的位移可以视为弹性体的刚体运动与弹性变形的叠加[2],Simpack动力学软件中柔性体的位移是通过基于瑞利-李兹方法计算得到,利用结构中各个子结构的低阶模态来构造近似程度较高的李兹集,弹性变形的微小变形矢量c(a,t)由阵型函数φi(a)和时间函数qi(t)的模态坐标线性表示:
(1)
利用瑞利-李兹法可以将弹性体的振动通过有限个阵型来表示,这样在保证计算精度的情况下有效的提高了计算速度.在有限元中设置前10阶模态计算,通过设置模型主节点[3]并提交Nastran计算,计算结果文件输入至Simpack中,最终生成弹性体模型文件[4],替换Simpack中的刚体模型.在动力学计算过程中,构架上的任意一点的位移可以视为弹性体的整体运动(刚性运动) 与弹性变形的叠加[5].
由图4可知,无附加装置的一阶扭转振型的无阻尼固有频率为39 Hz,有附加装置的一阶扭转振型的无阻尼固有频率为32 Hz.
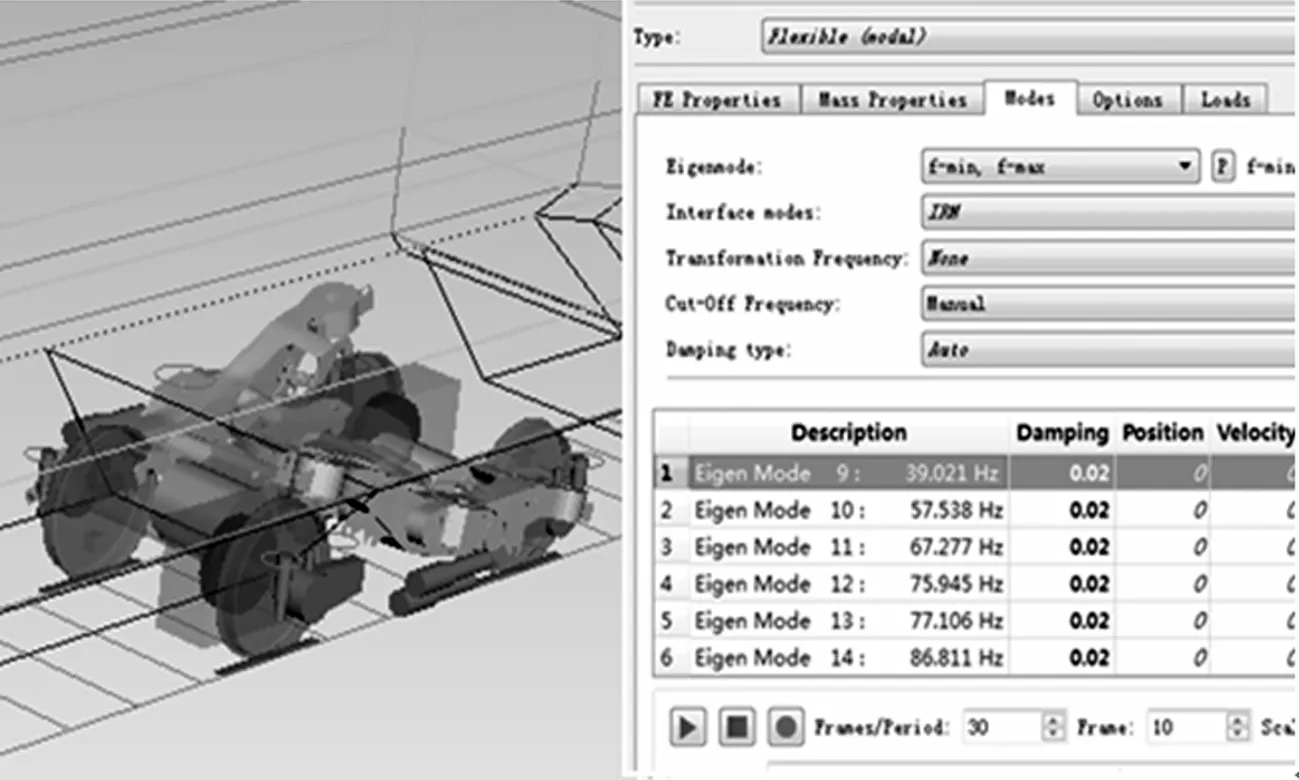
(a)无附加装置
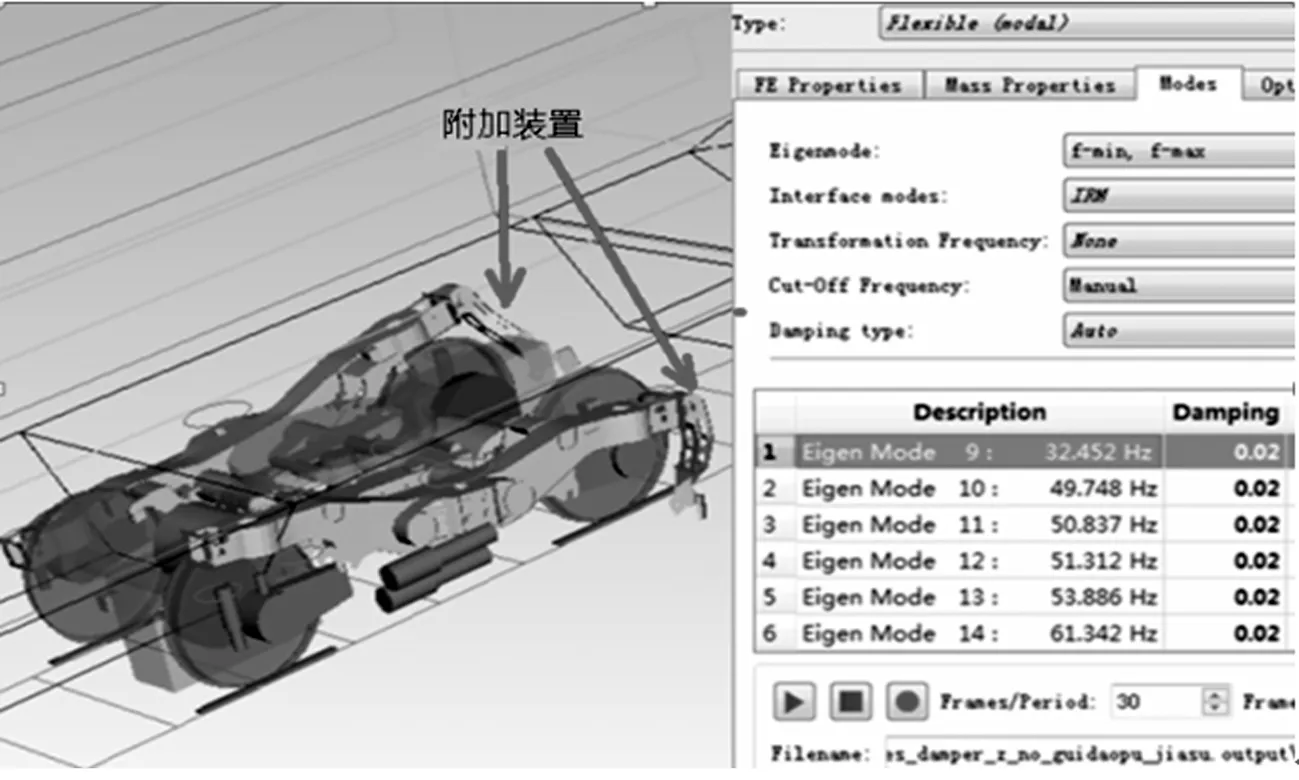
(b)有附加装置
通过Simpack的特征根计算,可以计算出整车状态下的有阻尼模态振型,构架的一阶扭转表现为2种振动频率,分别对应轮对不同的摇头相位.有附加装置构架扭转振型的有阻尼固有频率分别为31和36Hz.无附加装置构架扭转振型的有阻尼固有频率分别为33和41 Hz.
1.4 轮对动不平衡模型
轮对动不平衡产生的频率随着车辆速度的提高而提高,通过如下公式进行计算
(2)
高速列车的车速达到310 km/h时,动不平衡频率将接近30 Hz,速度继续提升,动不平衡频率有可能接近构架的一阶扭转频率.以往动不平衡采用轨道谱的形式施加,本文使用动不平衡块附加在轮对上模拟动不平衡量.日本铁路规定,新造车轮的不平衡量最大允许值为250 g·m,新干线车辆为50 g·m[6].根据国内动车组检修规程,高速动车组轮对的动不平衡量不超过50 g·m,而线路实测动不平衡量最大检测到接近150 g·m.本文以线路实测动不平衡超标值150 g·m作为仿真计算依据.此外,轮对动不平衡的相位将直接影响构架是否与该频率的激励产生共振.前后轮对正相位布置动不平衡块时,前后轮对动不平衡产生的激励相位相同,而反相位时,动不平衡激励相位相差180°.
1.5 计算工况
为充分体现动不平衡激励对构架扭转变形的影响,仿真时车辆在时速305 km/h基础上加速,最高达到376 km/h,在直线上运行,分别计算实测高速线路轨道谱和不加轨道谱两种工况,通过式(1)可以计算不同速度下的动不平衡激励.此外,计算前后轮对的动不平衡处于正反相位两种工况.
2 动不平衡激励对扭转变形的影响
首先分析动不平衡正反相位引起的构架扭转变形量.如图5所示.可见,同相位动不平衡激励对构架扭转的变形影响很小,最大幅值为0.09mm.而反相位动不平衡激励引起的最大变形幅值为0.65 mm.
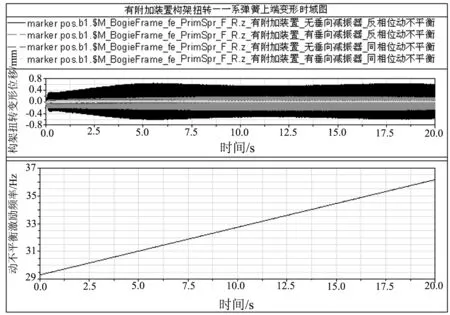
图5 正反相位动不平衡引起一系弹簧处的变形
为了进一步考察有附加和无附加装置的区别,后面的计算都在反相位基础上进行.如图6(a)所示,没有垂向减振器时,无附加装置在33.5Hz时,有较大的变形.而有附加装置的构架在31Hz和36 Hz时有较大的变形,见图6(b).当无一系垂向阻尼时,300~376 km/h速度区间动不平衡引起的扭转变形最大值,有附加装置为0.65 mm,无附加装置为0.58 mm,二者变形相差0.07 mm.当一系减振器正常发挥阻尼作用时,有附加装置构架扭转变形最大值由无阻尼作用时的0.65 mm下降为0.29 mm,而无附加装置构架扭转变形由0.58 mm下降为0.27 mm.有附加装置与无附加装置相比,变形仅增加了0.02 mm,相差较小.
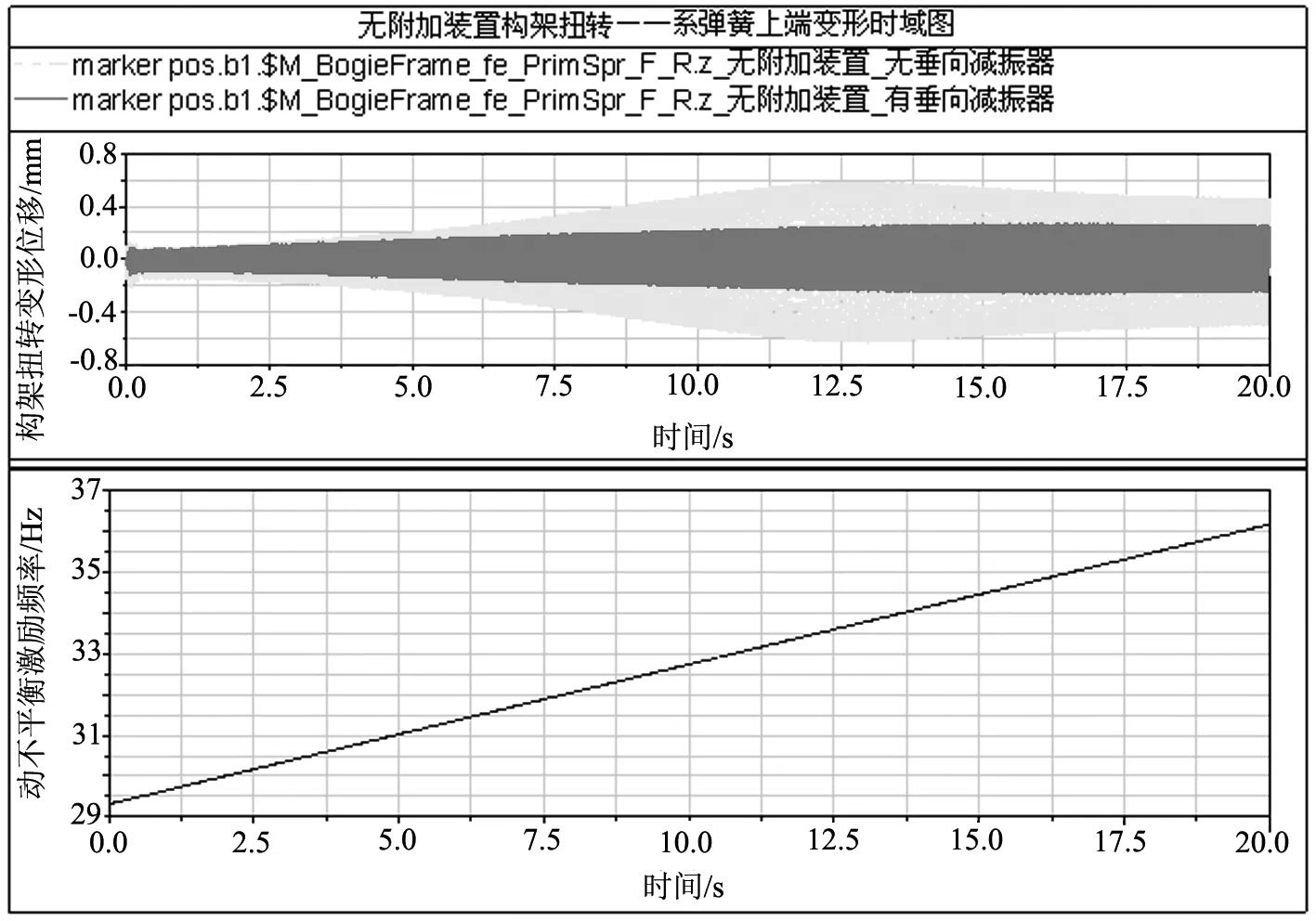
(a)无附加装置
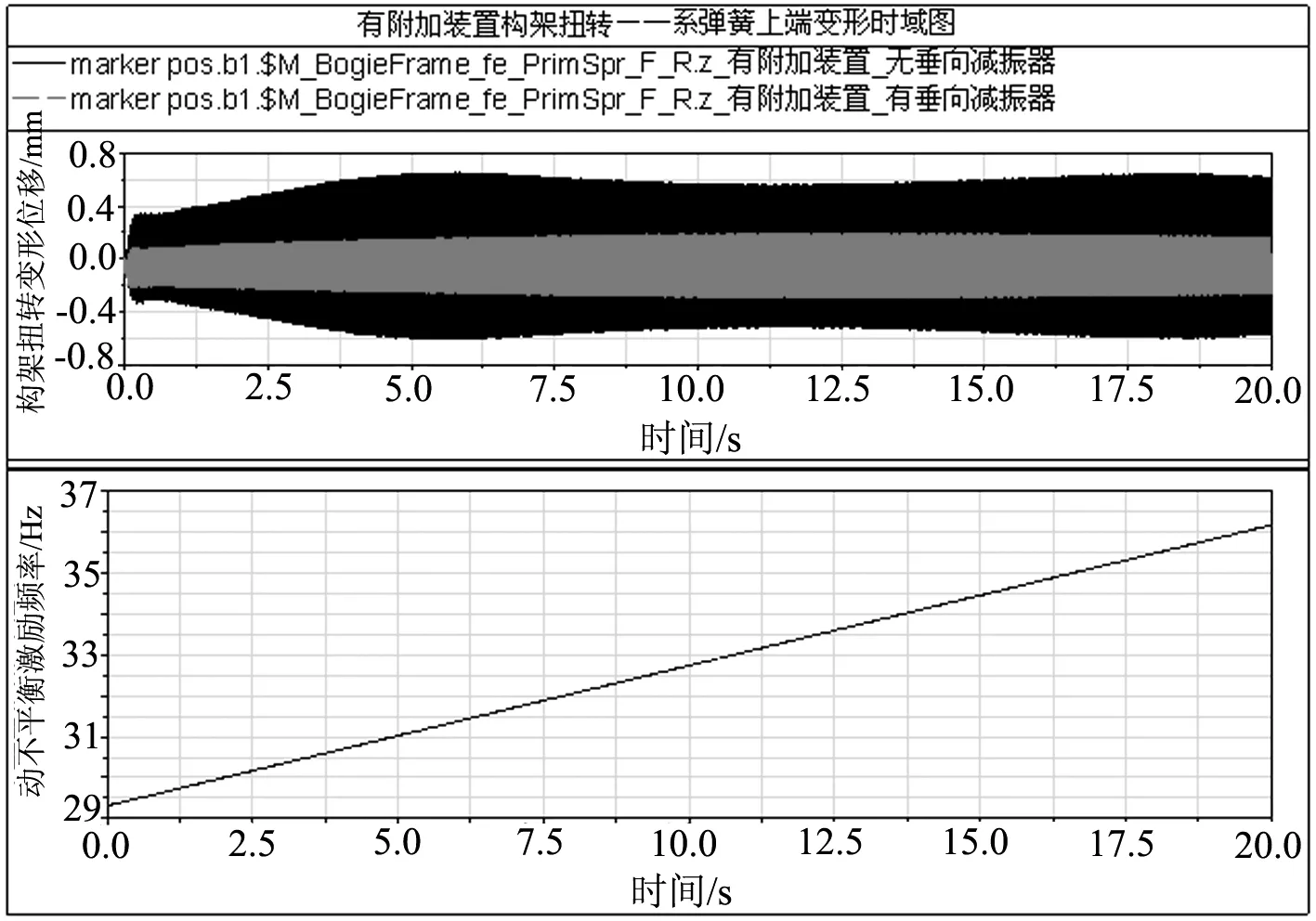
(b)有附加装置
从图7变形频谱图上更能直观显示其峰值频率.此外,没有一系垂向减振器作用时,有附加装置的峰值频率范围较无附加装置的宽,当减振器作用后二者相差不大.
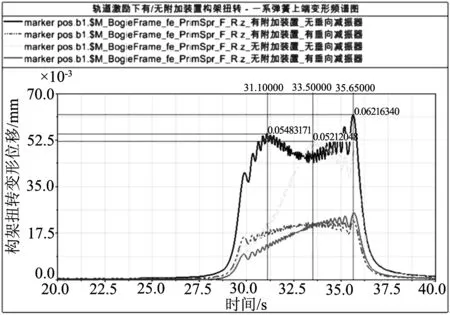
图7 构架在一系弹簧处的变形频谱图
3 轨道谱对扭转变形的影响
计算实测线路谱和动不平衡综合激励下的构架变形,见图8.速度依然由305 km/h加速到376 km/h,一系垂向减振器正常工作,无附加装置构架的扭转变形最大值为0.98 mm,有附加装置构架最大变形为0.88 mm.而之前没有轨道激励的计算结果为:在动不平衡激励下的构架扭转变形,无附加装置为0.27 mm,有附加装置的为0.29mm.可见,无附加装置动不平衡激励引起的构架扭转变形占综合激励变形的27.6%,有附加装置动不平衡激励引起的构架扭转变形占综合变形的33%.
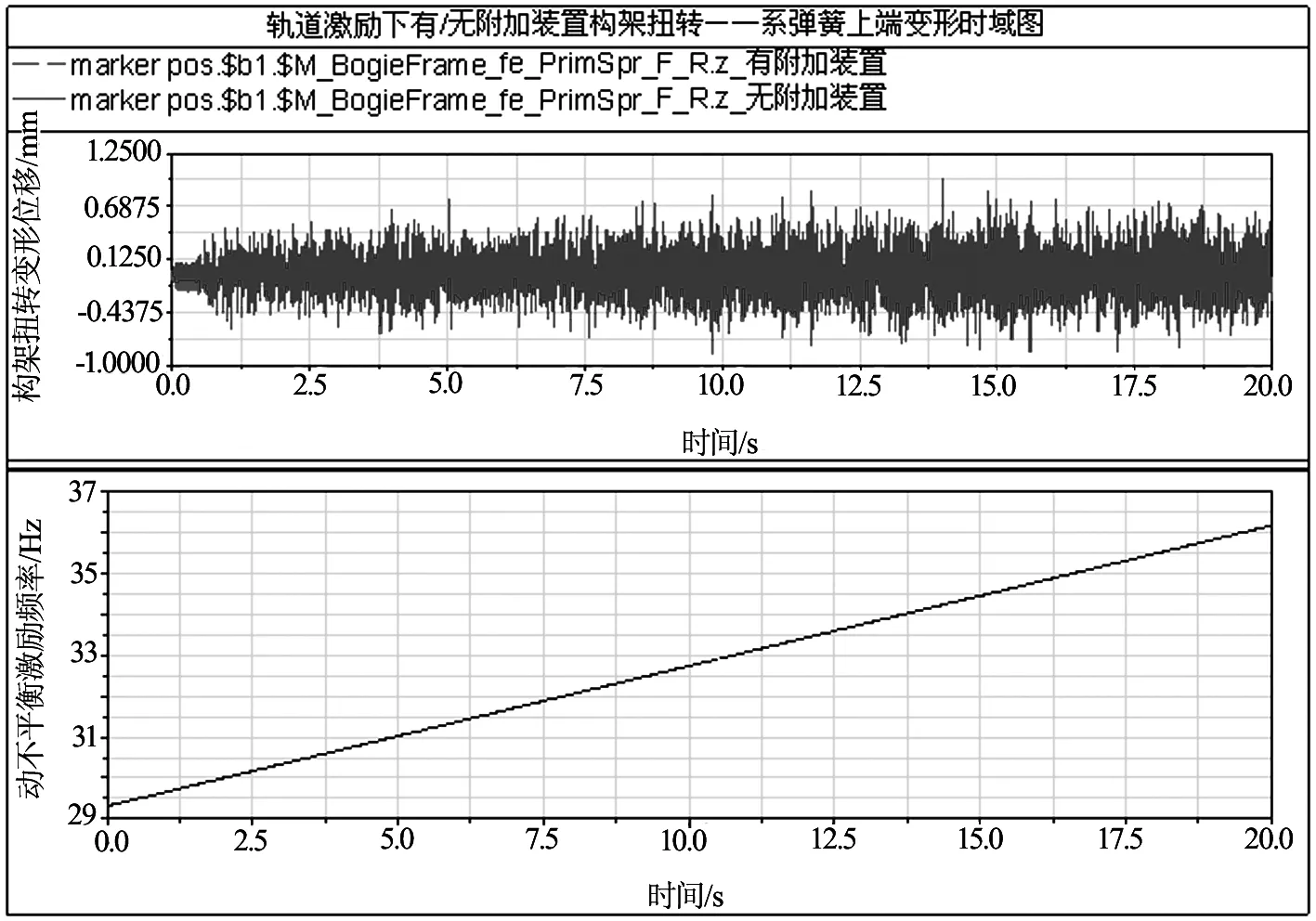
(a)构架一系弹簧处变形

(b)构架一系弹簧处变形频谱
4 应力与疲劳强度校核
在构架设计阶段,依据JISE4207标准进行强度校核[7]时考虑10‰的轨道扭曲量,换算到构架的设计扭转变形量约为3 mm.根据实测轨道谱和动不平衡综合激励产生的扭转变形计算结果,有附加装置构架变形为0.98 mm,无附加装置构架变形量为0.88 mm.其中动不平衡引起的变形,有附加装置构架为0.29 mm,占设计扭转变形量的9.7%,无附加装置构架为0.28 mm,占设计扭转变形量的9%.因此,疲劳强度校核可依据这一结论做适当调整[8],扭转变形增加到3.3 mm.经有限元计算,在此载荷条件下,构架最大主应力值为18.53 MPa(发生在横侧梁连接部位),见图9所示.
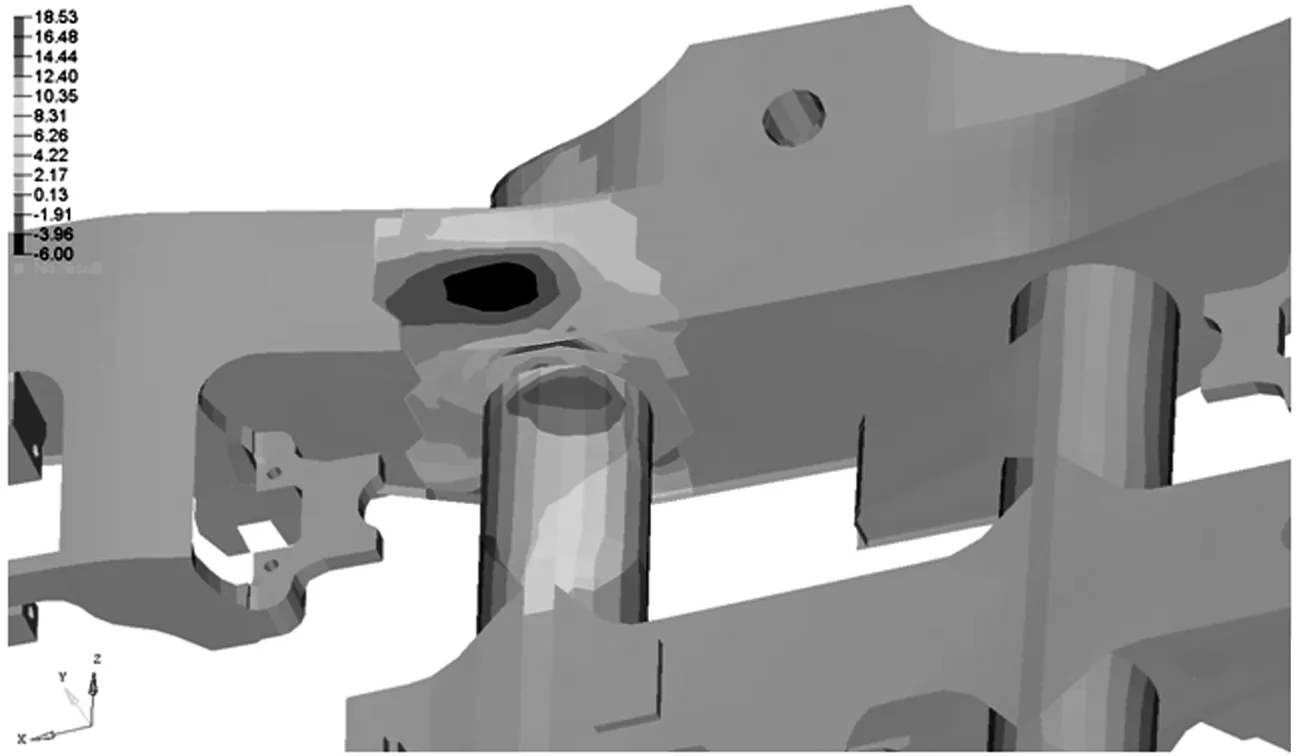
图9 构架强度计算3.3 mm扭转变形时最大主应力
5 结论
(1)含附加装置构架频率32.5 Hz,低于不含附加装置构架频率39.0 Hz.构架在动不平衡激励下的一阶扭转变形前者要比后者增加约0.02mm.垂向减振器有效降低了构架的扭转变形;
(2)动不平衡前后轮对的相位对构架扭转变形影响较大,反相位为最不利情况;
(3)动不平衡引起的构架扭转变形,有附加构架约为0.29 mm,占设计扭转变形量的9.7%,无附加构架约为0.28 mm,占设计扭转变形量的9%.因此考虑线路扭曲和构架动不平衡变形的综合影响,疲劳强度校核下的构架扭转变形增加为3.3 mm,计算得到构架最大主应力为18.53 MPa.
参考文献:
[1]南玲,宋荣荣,马卫华.垂向减振器对铁道车辆动力学性能的影响分析[J].机械,2009(4):9-13.
[2]刘键,石广田.弹性构架对车辆系统动力学影响研究[J].机械研究与应用,2016(1):117-121.
[3]包学海,池茂儒,卢耀辉.基于子结构法的车辆系统刚柔混合动力学建模方法研究[J].铁道机车车辆,2009(3):8-11.
[4]洪嘉振,刘锦阳.机械系统计算动力学与建[M].北京:高等教育出版社,2011.
[5]周素霞,陶永忠.Simpack9实例教程[M].北京:北京联合出版公司出版,2013.
[6]余凌晶.驱动系统及轮对不平衡对高速车辆动态性能影响的研究[D].北京:北京交通大学,2014.
[7]田葆栓.铁道车辆扭转载荷和扭转刚度设计及试验鉴定标准的分析研究[J].铁道车辆,2016(1):4-11.
[8]阳光武.机车车辆零部件疲劳寿命预测仿真[M].成都:西南交通大学,2003.

