一种新型压缩空气与抽水复合储能系统的热力学分析

姚尔人, 席光, 王焕然, 邹瀚森, 李瑞雄, 胡杨, 王志恒, 孙中国

(西安交通大学能源与动力工程学院, 710049, 西安)

随着传统化石能源储量的日益枯竭,开发替代性的清洁可再生能源已成为世界各国的共识[1]。风能、太阳能等可再生能源固有的随机性和波动性等特点是大规模利用该类能源的主要障碍[2],目前国内外学者一致认为储能技术是解决上述问题的有效途径[3]。

现有储能技术主要包括抽水蓄能、压缩空气储能、燃料电池以及超导电磁储能等[4],但适用于100 MW级及以上的大规模储能技术只有抽水蓄能技术(PHS)和压缩空气储能技术(CAES)[5]。虽然PHS储能容量和储能效率均较高,但是存在选址困难、建设周期长以及引起当地生态破坏等问题[6];CAES具有储能密度大、建设成本相对较低等优点,但传统CAES电能转换效率较低,并且存在补充化石燃料燃烧等问题[7]。随着近年来储热技术[8]的迅速发展,先进绝热压缩空气储能系统(AA-CAES)将储能过程中产生的压缩热回收并储存,在释能过程中利用这部分热量加热空气,从而与传统CAES系统相比不再依赖化石燃料[9]。Jubeh等基于热力学理论对比分析了CAES和AA-CAES,得出AA-CAES具有更高能量效率的结论[10]。Luo等通过对AA-CAES中热力学参数的进一步优化,使系统的能量效率达到68%[11],但AA-CAES仍存在响应速度慢等固有缺陷。

为解决上述PHS和CAES存在的不足,Wang等提出了一种兼具PHS和CAES特点的新型抽水压缩空气储能技术(PH-CAES),通过对该系统开展热力学分析,表明该系统具有较高的能量效率和较快的响应速度,以及大规模推广应用的潜力[12]。Yao等在此系统的基础上提出了一种恒压PH-CAES,进一步提升了系统的稳定性[13]。但是,目前PH-CAES的储能密度较低,系统需要巨大的储能容器以满足相应的大规模储能,因此降低了该系统的经济学性能。为解决上述问题,本文提出一种新型压缩空气与抽水复合储能系统(CA-PHES),并且通过对压力能和热能的高效梯级利用,实现了能量的高效转换。在建立该新型储能系统正确的理论模型基础上,对所提系统的热力学性能进行了变参数模拟计算分析。

1　系统描述

1.1　系统原理

CA-PHES系统如图1所示,主要设备包括压气机、透平机、水泵、水轮机、储气洞穴和水气共容舱等。储能过程分为两个阶段:第一阶段利用可再生能源驱动水泵工作,通过水泵向水气共容舱内注水,将水气共容舱内的空气压入储气洞穴中[14],待水气共容舱内充满水后,水泵停止工作,第一阶段的储能过程结束;第二阶段改用可再生能源驱动压气机将空气压缩至高压状态,并将高温压缩空气与来自储热器温度较低的储热介质进行热量交换(根据系统中工质的工作温度范围,本文选取矿物油作为系统的储热介质[15]),高压空气降温后继续升压,然后进入储气洞穴存储,而吸热升温后的载热介质进入储热器,将热量存储起来。为提高系统的变工况运行特性,设定压气机机组前两段为等压比压缩,并且设置压气机机组第二段的出口压力为水泵停止工作后储气洞穴内的空气压力,因此仅压气机机组的最后一段为变压比工作。

在系统释能过程的第一阶段,储存于储气洞穴内的高压空气经过节流后,进入水气共容舱并推动水气共容舱内的水进入水轮机发电[14],直至水气共容舱内的水排放完毕;在第二阶段,储气洞穴内和水气共容舱内的高压空气经过节流后,高压空气在换热器中与来自储热器的高温载热介质换热,升温后的高压空气进入透平机做功并排放至大气,而降温后的载热介质返回储热器,系统的释能发电过程无需补充燃料。

1.2　系统模型

为简化系统的数学模型,本文做出如下假设:

(1)系统处于稳定工作状态;

(2)空气为理想气体,满足理想气体状态方程;

(3)储气洞穴和水气共容舱内充气和放气过程为近似等温过程[16-17];

(4)忽略储热器中载热介质对环境的热耗散效应,并认为载热介质的热容量等于所储存空气的热容量[18];

(5)忽略换热器、储气洞穴、水气共容舱以及管道的压力损失。

图1　CA-PHES系统示意图

基于以上假设,根据质量和能量守恒定律,对系统中各设备进行数学建模。

1.2.1压气机压气机的出口空气温度为

(1)

式中:Tc,in是压气机入口空气温度;κ为空气的绝热指数;πc是压气机的压比;ηc为压气机的等熵效率。

压气机输入功率为

(2)

1.2.2透平机透平机的出口空气温度为

(3)

式中:Tt,in是透平机入口空气温度;πt是透平机的膨胀比;ηt是透平机的等熵效率。

透平机的输出功率为

(4)

1.2.3换热器换热器的热负荷可由下式计算

(5)

式中:cp是流体的比定压热容;下标hf和cf分别代表换热器中的热流体和冷流体。

1.2.4水泵水泵的输入功率为

(6)

1.2.5水轮机水轮机输出功率为

(7)

系统的能量效率是系统输出总功量Wout与系统总消耗功量Win之比

(8)

式中:tht、tt、tp、tc分别为水轮机、透平机、水泵和压气机的工作时间。

2　计算与分析

在系统额定输出功率为10 MW、发电时间为10 h、总输出容量为100 MW·h的工程背景条件下,CA-PHES系统中各设备的运行参数如表1所示。

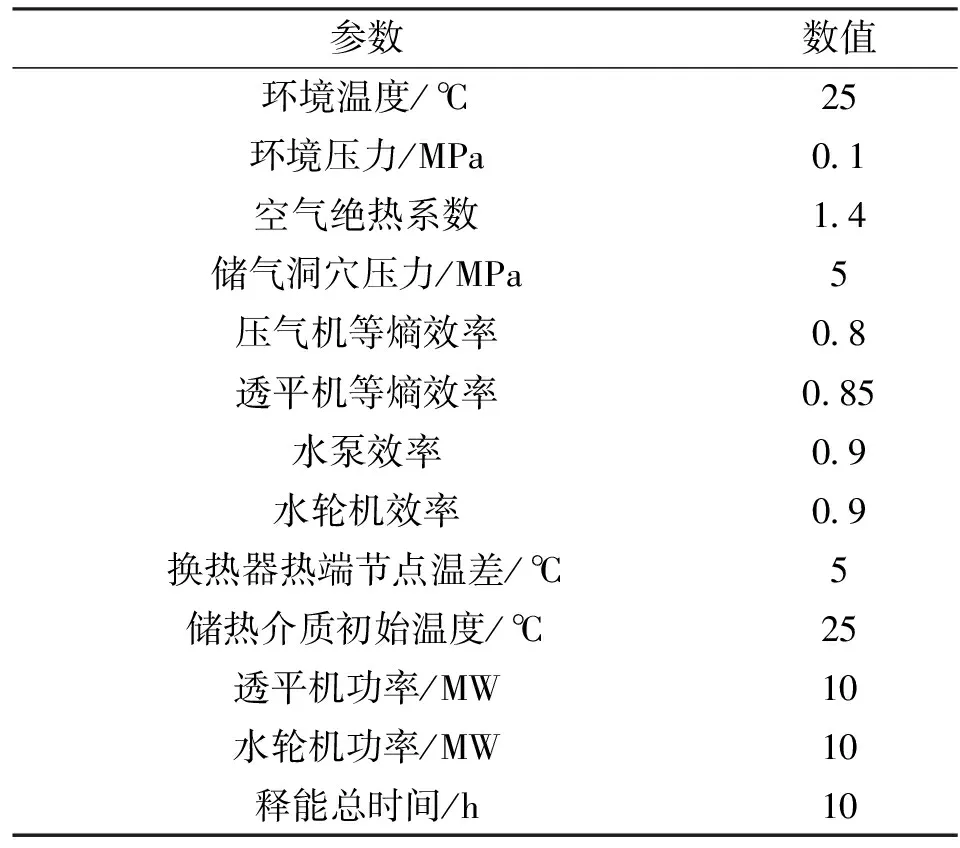
表1　CA-PHES系统运行参数值

根据CA-PHES系统的工作原理可知,系统通过储气洞穴和水气共容舱将CAES和PHS耦合,选取表1中的运行参数,基于理想气体状态方程、质量和能量守恒定律,并且联立式(1)～(7),得到储气洞穴体积Vsv和水气共容舱体积Vsq的计算公式为

(9)

式中:psv,max、psv,min分别是储气洞穴内空气的最高与最低压力;ρ为水的密度;T0为环境温度。

本文在MATLAB中建立CA-PHES系统的热力计算平台,从而完成对系统的热力学模拟,具体的热力学计算流程如图2所示。

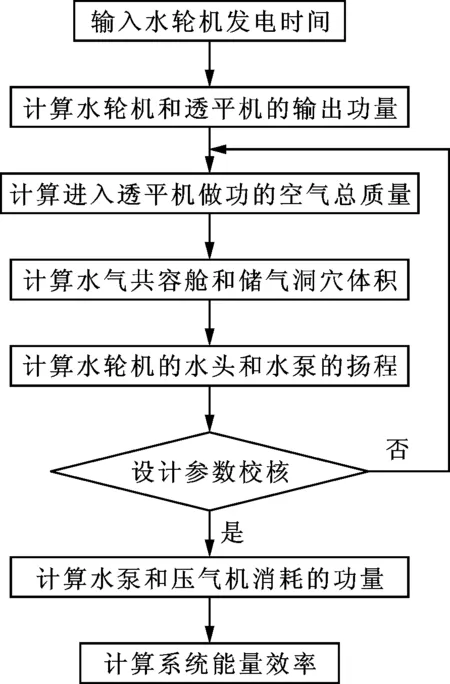
图2　CA-PHES系统计算流程图

2.1　水轮机发电时间对系统的影响

图3为系统中水气共容舱体积随水轮机工作时间的变化。从图中可以看出:随着水轮机工作时间的增加,水气共容舱的体积增大,在储气洞穴内空气最大压力、最小压力和水轮机发电功率一定的条件下,水轮机工作时间延长导致水轮机总输出功量升高,水轮机需要更多的水量以保证输出相应的电能,因此水气共容舱的体积增大;当水轮机工作时间确定和储气洞穴内空气的最高压力保持不变时,随着系统储气洞穴内空气的最低压力逐渐降低,水轮机水头相应降低,因此需要更多水量以满足水轮机的输出功量,水气共容舱的体积相应增大。

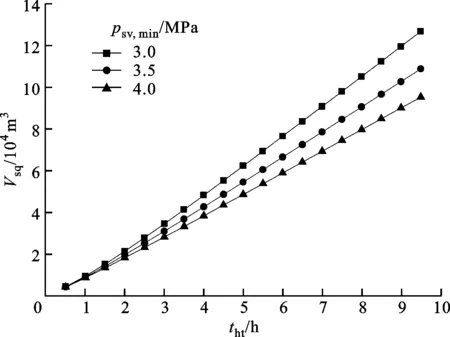
图3　水轮机工作时间对水气共容舱体积的影响

图4为系统中储气洞穴体积随水轮机工作时间的变化。由图可知,随着水轮机工作时间的延长,系统中储气洞穴的体积增大。根据式(9)可知,在系统储气洞穴最大压力和最小压力一定的工况下,尽管水轮机工作时间延长使得进入透平机膨胀做功的空气质量减少,但是水气共容舱的体积对系统储气洞穴体积变化起主导作用,因此储气洞穴体积增大;在不同系统储气洞穴最低压力条件下,由于系统储气洞穴的最高压力为5 MPa,因此随着系统储气洞穴内空气最低压力的升高,系统储气洞穴内空气的压差降低,根据质量和能量守恒定理,需要更大的储气洞穴体积以满足系统的工作要求。此外,通过推导式(9),也可得出相同的结论。

图4　水轮机工作时间对储气洞穴体积的影响

图5为系统中水轮机水头随水轮机工作时间的变化。从图中可以看出,随着水轮机工作时间的延长,系统中水轮机的水头降低。这是因为在释能过程中,系统所储存的压力能通过水轮机和透平机转换为机械能,进而对外输出电能,因此在系统储存压力能一定的条件下,随着水轮机工作时间的增长,由水轮机释放的压力能增多,而通过透平机释放的压力能减少,即水轮机的水头随水轮机工作时间的增长而降低,且逐渐接近系统储气洞穴内空气的最低压力所对应的水头。

图5　水轮机工作时间对水轮机水头的影响

图6为系统中水泵扬程随水轮机工作时间的变化。由于水轮机工作时间延长使得进入水轮机做功的水量增加,从而使得水气共容舱体积增大(如图3所示),因此在系统的储能过程中,需要通过水泵将更大体积的水泵回至水气共容舱中,从而将水气共容舱内的带压气体压回至储气洞穴中,故水泵的扬程升高。

图6　水轮机工作时间对水泵扬程的影响

图7a为系统能量效率随水轮机工作时间的变化。由图可知,随着水轮机工作时间的延长,以水轮机工作时间1.5 h为分界,当水轮机工作时间小于1.5 h时,随着水轮机工作时间的延长,系统的能量效率缓慢升高,而当水轮机工作时间大于1.5 h时,随着水轮机工作时间的延长,系统的能量效率大幅下降,尽管不同的储气洞穴内空气最低压力使得系统的能量效率变化范围有所不同,但是系统的能量效率均在水轮机工作时间为1.5 h左右达到峰值。根据式(8)可知,在系统总输出功量为100 MW·h的条件下,系统的能量效率随系统的总消耗功量升高逐渐降低,而随系统的总消耗功量降低逐渐升高。因此,从图7b中可以看出,随水轮机工作时间的延长,系统的总消耗功量逐渐降低,对应图7a中系统能量效率的升高趋势,当水轮机工作时间为1.5 h时,系统的总消耗功量最低,对应图7a中系统的最高能量效率点,随着水轮机工作时间的继续延长,系统的总消耗功量逐渐升高,对应图7a中系统能量效率的降低趋势。根据式(8)还可知,系统的总消耗功量由压气机的消耗功量和水泵的消耗功量两部分组成,随着水轮机工作时间的延长,水泵的扬程以及由于水气共容舱体积增大所引起的水泵泵水量均逐渐升高(如图3和图6所示),因此水泵的消耗功量如图7c所示逐渐升高,特别是当水轮机工作时间达到3 h后,水泵泵水量的大幅升高(如图3所示)导致水泵消耗功量大幅升高,且升高幅度远高于压气机消耗功量的降低幅度。这使得系统的总消耗功量在水轮机工作3 h以后大幅增加,从而导致系统的能量效率在水轮机工作3 h以后大幅降低。

(a)对系统能量效率的影响

(b)对系统总消耗功量的影响

(c)对压气机和水泵消耗功量的影响图7　水轮机工作时间对系统评价指标的影响

2.2　设备性能对系统的影响

从图3～7可以看出,当系统中水轮机工作时间为1.5 h时,系统的能量效率最高,因此基于此工况进一步分析系统能量效率随各设备效率以及换热器节点温差的变化规律,结果如图8所示。从图8a中可以看出,与水轮机和水泵相比,提升压气机和透平机等熵效率能够更加明显地提升系统的能量效率。这是因为在本文的计算工况下,水轮机的输出功量和水泵消耗功量分别占系统的总输出功量和总消耗功量的比例较小。从图8a还可以看出,透平机等熵效率的提升可以大幅提升系统的能量效率;从图8b中可以看出,随着换热器节点温差从1 ℃升高到20 ℃,系统的能量效率从72.51%降低到68.04%。

(a)设备等熵效率的变化

(b)换热器热端节点温差的变化图8　　　　系统设备等熵效率和换热器热端节点温差对系统能量效率的影响

2.3　压气机和透平机压比对系统的影响

图9为系统能量效率随系统中透平机械设备内压比分配的变化,当压气机机组各段压比变化时,透平机机组各段膨胀比保持不变;当透平机机组各段膨胀比变化时,压气机机组各段压比保持恒定。由图9可知:当压气机机组第一段压比升高时,压气机机组消耗的总压缩功降低,导致系统的能量效率逐渐升高,当压气机机组第一段压比达到7.99时,系统的能量效率达到最大峰值(71.19%),随着压气机机组第一段压比的继续升高,系统的能量效率降低;当透平机机组第一段膨胀比升高时,透平机机组对储能过程中所储存的圧缩热利用率升高,因此系统的能量效率增加,在透平机机组第一段膨胀比为5.45时,系统的能量效率达到最高值(71.16%),随着透平机机组第一段膨胀比的继续升高,系统的能量效率降低。

图9　压气机和透平机压比对系统能量效率的影响

为探求系统的最高能量效率,本文基于遗传算法,以压气机机组第一段压比(取值范围为3.53～12.47)和透平机机组第一段膨胀比(取值范围为3.40～11.59)为两个决策变量,以系统的能量效率为目标函数,对系统进行多目标优化。经过优化后发现,在系统总输出容量为100 MW·h,压气机机组3段压比分配为3.53、12.77和1.14,以及透平机机组两段膨胀比分别为3.4和11.15的工况下,系统的最高能量效率可达71.82%。

3　结　论

基于热力学定律和能量梯级利用的原则,本文提出一种将抽水蓄能与压缩空气储能耦合的新型抽水压缩气体复合储能系统,在系统额定输出功率为10 MW、发电时间为10 h、总输出容量为100 MW·h的运行工况条件下,通过对系统进行热力学建模,获得了系统主要运行参数对系统性能的影响规律,系统分析结果如下。

(1)随着水轮机工作时间的延长,水气共容舱、储气洞穴的体积和水泵的扬程都有所增大,而水轮机的水头逐渐降低。

(2)在水轮机工作时间为1.5 h、透平机工作时间为8.5 h的条件下,较高的储气洞穴最低压力使得系统的能量效率升高,在通过多目标优化手段进一步优化压气机机组和透平机机组的压比分配后,系统的能量效率可达到71.82%。

(3)提升设备的效率可以提升系统的能量效率,特别是提升透平机等熵效率对提高系统的能量效率效果最为明显。

参考文献:

[1]BAZMI A A, ZAHEDI G. Sustainable energy systems: role of optimization modeling techniques in power generation and supply: a review [J]. Renewable and Sustainable Energy Reviews, 2011, 15(8): 3480-3500.

[2]姚尔人, 王焕然, 席光. 一种压缩空气储能与内燃机技术耦合的冷热电联产系统 [J]. 西安交通大学学报, 2016, 50(1): 22-27.

YAO Erren, WANG Huanran, XI Guang. A novel combined cooling heating and power system with coupled compressed air energy storage and combustion engine [J]. Journal of Xi’an Jiaotong University, 2016, 50(1): 22-27.

[3]MAHLIA T M I, SAKTISAHDAN T J, JANNIFAR A, et al. A review of available methods and development on energy storage; technology update [J]. Renewable and Sustainable Energy Reviews, 2014, 33(33): 532-545.

[4]张伟德, 徐钢, 刘文毅, 等. 典型压缩空气蓄能(CAES)电站热力学分析与系统优化 [J]. 现代电力, 2013, 30(2): 41-47.

ZHANG Weide, XU Gang, LIU Wenyi, et al. Thermodynamic analysis and optimization of a typical compressed air energy storage (CAES) power plant [J]. Modern Electric Power, 2013, 30(2): 41-47.

[5]YAO E, WANG H, WANG L, et al. Thermo-economic optimization of a combined cooling, heating and power system based on small-scale compressed air energy storage [J]. Energy Conversion and Management, 2016, 118: 377-386.

[6]张新敬, 陈海生, 刘金超, 等. 压缩空气储能技术研究进展 [J]. 储能科学与技术, 2012, 1(1): 26-40.

ZHANG Xinjing, CHEN Haisheng, LIU Jinchao, et al. Research progress in compressed air energy storage system: a review [J]. Energy Storage Science and Technology, 2012, 1(1): 26-40.

[7]陈海生, 刘金超, 郭欢, 等. 压缩空气储能技术原理 [J]. 储能科学与技术, 2013, 2(2): 146-151.

CHEN Haisheng, LIU Jinchao, GUO Huan, et al. Technical principle of compressed air energy storage system [J]. Energy Storage Science and Technology, 2013, 2(2): 146-151.

[8]DINCER I, ROSEN M. Thermal energy storage: systems and applications [M]. 2nd ed. Chichester, UK: John Wiley & Sons, 2011: 85-90.

[9]张远, 杨科, 李雪梅, 等. 先进绝热压缩空气储能的冷热电输出特性研究 [J]. 热能动力工程, 2013, 28(2): 134-138.

ZHANG Yuan, YANG Ke, LI Xuemei, et al. Study of the cooling, heating and power output charcteristics of an advanced adiabatic compressed air energy storage [J]. Journal of Engineering for Thermal Energy and Power, 2013, 28(2): 134-138.

[10] JUBEH N M, NAJJAR Y S H. Green solution for power generation by adoption of adiabatic CAES system [J]. Applied Thermal Engineering, 2012, 44: 85-89.

[11] LUO X, WANG J, KRUPKE C, et al. Modelling study, efficiency analysis and optimisation of large-scale adiabatic compressed air energy storage systems with low-temperature thermal storage [J]. Applied Energy, 2016, 162: 589-600.

[12] WANG H, WANG L, WANG X, et al. A novel pumped hydro combined with compressed air energy storage system [J]. Energies, 2013, 6(3): 1554-1567.

[13] YAO E, WANG H, LIU L, et al. A novel constant-pressure pumped hydro combined with compressed air energy storage system [J]. Energies, 2015, 8(1): 154-171.

[14] WOLF D. Methods for design and application of adiabatic compressed air energy: storage based on dynamic modeling [D]. Baukem, Germany: Ruhr-Universität Bochum, 2011.

[15] 韩中合, 周权, 王营营, 等. 先进绝热压缩空气储能(AA-CAES)系统一种结构优化方案 [J]. 太阳能学报, 2016, 37(3): 629-635.

HAN Zhonghe, ZHOU Quan, WANG Yingying, et al. Analysis of two sorts of configurations of AA-CAES system [J]. Acta Energiae Solaris Sinica, 2016, 37(3): 629-635.

[16] 张远, 杨科, 李雪梅, 等. 基于先进绝热压缩空气储能的冷热电联产系统 [J]. 工程热物理学报, 2013, 34(11): 1991-1996.

ZHANG Yuan, YANG Ke, LI Xuemei, et al. A combined cooling, heating and power (CCHP) system based on advanced adiabatic compressed air energy storage (AA-CAES) technology [J]. Journal of Engineering Thermophysics, 2013, 34(11): 1991-1996.

[17] LIU J, WANG J. A comparative research of two adiabatic compressed air energy storage systems [J]. Energy Conversion and Management, 2016, 108: 566-578.

[18] 韩中合, 刘士名, 周权, 等. 恒壁温储气模型下先进绝热压缩空气储能系统性能分析 [J]. 中国电机工程学报, 2016, 36(12): 3373-3381.

HAN Zhonghe, LIU Shiming, ZHOU Quan, et al. Performance analysis of AA-CAES system with constant wall-temperature air storage model [J]. Proceedings of the CSEE, 2016, 36(12): 3373-3381.