布尔环的一个注记
邵 勇,崔 璐
(西北大学 数学学院,陕西 西安 710127)
若环(R,+,·)的每个元素都是幂等的,即对任意的a∈R,有a2=a,则称(R,+,·)为布尔(Boolean)环[1-2]。布尔环是环论中重要的研究对象,它在命题逻辑,计算机科学及格论研究中扮演了重要角色[3-5],并且在布尔代数的研究中也是必不可少的[6-8]。
设(R,+,·)为环,若存在自然数p≥2,对任意的a∈R,有ap=a,则此环为Jacobson环[9-11]。显然,布尔环是Jacobson环;但是Jacobson环不一定是布尔环,例如,整数模7的剩余类环。当p=2时,Jacobson环显然是布尔环。本文的Jacobson环(R,+,·)均指满足对任意的a∈R,存在某个自然数p>2,有ap=a的环。有不少学者从不同的角度给出Jacobson环成为布尔环的条件[11-12]。
对于特征为2的含幺Jacobson环,当自然数p满足一定条件,例如,当p=2n-2,n>1,或者p=2n-5,n≥3,此时Jacobson环(R,+,·)成为布尔环[12]。
1 预备知识
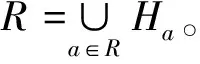
2 主要结果
本节将研究特征为2的Jacobson环的性质,在此基础上,得到特征为2的Jacobson环成为布尔环的条件。与文献[12]强调的含幺Jacobson环不同,本文不要求Jacobson环含有幺元。所获结果将推广文献[12]的主要结论。
特征为2的Jacobson环具有如下性质。

1) (a0+a)k=a0+ak;
2)ak=a;
3) (R,+,·)为布尔环。

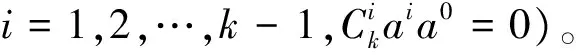
2)由结果1),有(a0+a)k=a0+ak,又特征为2,则a+a=0。故有
a0+a=(a0+a)p=
(a0+a)k(a0+a)=
(a0+ak)(a0+a)=
a0+ak+ak+1+a=
a0+ak+a+a=
a0+ak,
则有ak=a。
3)因对任意的a∈R,ak+1=a,由结果2)可知,ak=a,则有ak+1=a2,故对任意的a∈R,a2=a,即(R,+,·)为布尔环。
设(R,+,·)是特征为2的Jacobson环时,由(R,·)是群并半群可得到如下的结论。
引理2设(R,+,·)是特征为2的Jacobson环,若p=2n+1,则(R,+,·)为布尔环;特别地,若任意的a∈R,a3=a,则(R,+,·)为布尔环。
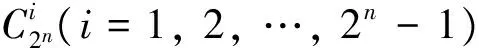
由文献[12]的引理6,对于特征为2的含幺Jacobson环(R,+,·),当p=2n+1,(R,+,·)会成为布尔环,本引理证明对于一般的特征为2的Jacobson环,满足p=2n+1,同样成为布尔环。
对于Jacobson环,可得如下结论。
定理1若Jacobson环(R,+,·)满足下列条件之一:
1)p=2n-2,n>1;
或者
2) (R,+,·)特征为2,且p=2n-5,n≥3,则(R,+,·)为布尔环。
为证明定理1,需要证明如下引理。
引理3设(R,+,·)是特征为2的Jacobson环,若p=2n-(2k1+2k2-1),则对任意的a∈R,有a2k1=a2k2。
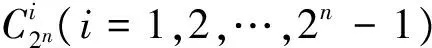
a0+a2n=(a0+a)2n=
(a0+a)2k1+2k2=
(a0+a)2k1·(a0+a)2k2=
(a0+a2k1)(a0+a2k2)=
a0+a2k1+a2k2+a2k1+2k2=
a0+a2k1+a2k2+a2n。
故a2k1+a2k2=0,由(R,+,·)特征为2可得a2k1=a2k2。
下证定理1。
1) 对任意的a∈R,有ap=a,由p为偶数可得-a=(-a0)a=(-a0)pa=a0a=a,故a+a=a+(-a)=0,这表明(R,+,·)的特征为2。
由引理3可知,若任意的a∈R,a2n-(2k1+2k2-1)=a,则有a2k1=a2k2,现取k1=1,k2=0,则有a2n-2=a,进一步有a2=a,从而(R,+,·)为布尔环。
2)在引理3中,取k1=2,k2=1,则有a2n-5=a,进一步有a2=a4,又存在a-1∈Ha,使得a·a-1=a0,则在a2=a4两端同时乘上a-1,得a3=a,由引理2,(R,+,·)为布尔环。
由文献[12]的定理5可知,若含幺Jacobson环(R,+,·),满足p=2n-2,n>1;或者对于特征为2的含幺Jacobson环(R,+,·),满足p=2n-5,n>3,则Jacobson环(R,+,·)会成为布尔环。本引理证明对于特征为2的一般Jacobson环,p满足相同条件同样可成为布尔环。
不难证明,对特征为2的Jacobson环,可得如下结论。
定理2设(R,+,·)是特征为2的Jacobson环,若同时满足下列条件:
1)p=2q+2m+1,q∈N,m∈{1,2,…,2q-1-1};
2) 2q-2m=2r+2s,r,s∈N,q>r>s≥1;
3) (2r-2s)|2m,
则(R,+,·)为布尔环。
证明已知(2r-2s)|2m,则有2m=l·(2r-2s),又a2q+2m+1=a,则有
a2q+1=a2q+2m+1·a2q-2m-1=
a·a2q-2m-1=a2q-2m。
因(R,·)为群并半群,则有
a0+a2q-2m=a0+a2q+1=
(a0+a)2q+1=
(a0+a)2q-2m=
(a0+a)2r+2s=
(a0+a)2r·(a0+a)2s=
(a0+a2r)·(a0+a2s)=
a0+a2r+a2s+a2r+2s=
a0+a2r+a2s+a2q-2m。
由此可得a2r=a2s,故有a2r-2s=a0,则有
a2q+1=a2q+1·a0=a2q+2r-2s+1=
…=a2q+l(2r-2s)+1=a2q+2m+1=a。
由引理2可知(R,+,·)为布尔环。
推论1设(R,+,·)是特征为2的Jacobson环若同时满足下列条件:
1)p=2q+2m+1,q∈N,m∈{1,2,…,2q-1-1};
2) 2q-2m=2r+1+2r,r∈N,q-1>r≥1,
则(R,+,·)为布尔环。
证明由2q-2m=2r+1+2r,则有2m=2q-(2r+1+2r)=2r(2q-r-3),故2r+1-2r=2r|2m,则由定理2可知(R,+,·)为布尔环。
不难发现,对于定理1中的第2)种情形:(R,+,·)是特征为2的Jacobson环,若p=2n-5,则(R,+,·)为布尔环。当n>3时,此情形可包含在定理2中,取
p=2n-5=2n-1+2n-1-5=
2n-1+(2n-1-6)+1
令q=n-1,2m=2n-1-6,则有
2q-2m=2n-1-(2n-1-6)=6=
22+21=2r+1+2r(取r=1)。
则由推论1可知(R,+,·)为布尔环。
易证对于特征为2的Jacobson环也有如下结论。
推论2设(R,+,·)是特征为2的Jacobson环且满足p=2n-(3·2l-1),n,l∈N且n-3≥l,则(R,+,·)为布尔环。
证明因n-3≥l,则
3·2l≤3·2n-3<4·2n-3=2n-1,
故有
p=2n-(3·2l-1)=2n-1+(2n-1-3·2l)+1
取q=n-1,2m=2n-1-3·2l,则
2q-2m=2n-1-(2n-1-3·2l)=
3·2l=2l+1+2l,
由推论1可知(R,+,·)为布尔环。
推论3设(R,+,·)是特征为2的Jacobson环,若同时满足下列条件:
1)p=2q+2m+1,q∈N,m∈{1,2,…,2q-1-1};
2) 2q-2m=2r+2s,r,s∈N,r>s≥1;
3)q=(r+1)+k(r-s),k∈N+,
则(R,+,·)为布尔环。
证明由所给条件可得
2m=2q-2r-2s=
2(r+1)+k(r-s)-2r-2s=
2s(2(r+1)+k(r-s)-s-2r-s-1)=
2s(2(k+1)(r-s)+1-2r-s-1)=
2s(2·2(k+1)(r-s)-2r-s-1)=
2s[(2(k+1)(r-s)-2r-s)+(2(k+1)(r-s)-1)]=
2s[2r-s((2r-s)k-1)+((2r-s)k+1-1)]=
2s[2r-s(2r-s-1)]×
((2r-s)k-1+(2r-s)k-2+…+2r-s+1)+
(2r-s-1)×((2r-s)k+(2r-s)k-1+…+
2r-s+1)]=2s(2r-s-1)×[2·((2r-s)k+
(2r-s)k-1+…+2r-s)+1]=(2r-2s)×
[2·((2r-s)k+(2r-s)k-1+…+2r-s)+1]。
则有(2r-2s)|2m,由定理2可知(R,+,·)为布尔环。
定理3设(R,+,·)是Jacobson环,若满足p=2r+1+2r,r∈N,则(R,+,·)为布尔环。
证明由定理1中1)的证明可知,若p为偶数,则(R,+,·)特征为2。任意的a∈R,由(R,·)是群并半群可得
a0+a=(a0+a)2r+1+2r=
(a0+a)2r+1(a0+a)2r=
(a0+a2r+1)(a0+a2r)=
a0+a2r+a2r+1+a2r+2r+1=
a0+a2r+a2r+1+a。
故有a2r+1=a2r,从而
a2r+2=a2r+1+2r+1=
a2r+1·a2r+1=
a2r·a2r+1=a2r+2r+1=ap=a。
又由于
a2r+2=a2r+1+2r+1+2r-2r=
a2r+1+2r·a2r+1-2r=
ap·a2r=a·a2r=a2r+1。
故有a2r+1=a,由引理2可知(R,+,·)为布尔环。
参考文献:
[1]STONE M H. The theory of representations of Boolean algebras[J]. Amer Math Soc, 1936, 40:37-111.
[2]丰建文, 詹棠森. 可补半环上的同余[J]. 系统科学与数学, 2010, 24(6): 61-65.
[3]高平安, 蔡自兴. 有限布尔环上的自动机[J].小型微型计算机系统, 2006, 27(7): 1266-1269.
[4]STEVEN G. Introduction to Boolean Algebras[M].New York: Springer, 2009.
[5]孙瑶, 王定康. 布尔环上的分支Groebner基算法[J]. 系统科学与数学, 2009, 29(9): 1266-1277.
[6]朱秉涛. 关于布尔代数公理的独立性问题[J].数学研究与评论, 1987, 7(1): 167-170.
[7]STANKOVIC R S, ASTOLA J. From Boolean Logic to Switching Circuits and Automata:Towards Modern Information Technology[M].New York: Springer, 2011.
[8]陈露. 布尔代数的直觉T-S 模糊子代数的直积[J]. 西北大学学报(自然科学版), 2011,41(5): 781-785.
[9]王尧. 由环的周期性和Jacobson性质确定的根[J].河北师范大学学报(自然科学版), 1999,23(3): 305-307.
[10] 谢邦杰. 关于周期环与Jacobson环的几个定理[J]. 数学研究与评论, 1982, 2(2): 17-19.
[11] MIGUEL F, MICHAEL M P. A note on Jacobson rings and polynomial rings[J]. Proceedings of The American Mathematical Society, 1989,105(2): 281-286.
[12] CHAJDA I, SVRCEK F. The rings which are Boolean[J]. Discussiones Mathematicae General Algebra & Applications,2011, 31(2): 175-184.
[13] PETRICH M, REILLY N R. Completely Regular Semigroups[M]. New York: Wiley, 1996.
[14] 赵春来, 徐明曜. 抽象代数I[M]. 北京: 北京大学出版社, 2008.
[15] 盛德成. 抽象代数[M]. 北京: 科学出版社,2000.

