GNSS接收机天线相位中心垂向偏差检测

周广勇　余庆滨

GNSS接收机天线相位中心垂向偏差检测

周广勇1,2余庆滨1

（1.广东省计量科学研究院 2.广东省现代几何与力学计量技术重点实验室）

为准确测出GNSS接收机天线相位中心垂向偏差，在超短基线静态相对定位的基础上，给出一种倾斜测量法。由卧轴多齿分度台提供标准的旋转角，将待测接收机天线倾斜多组角度，其余4台接收机进行同步静态观测，解算出待测天线的多组坐标；再根据几何关系得出绝对垂向偏差。该方法中配合的天线无需已知相位中心偏差。通过分析经不同的数据处理方法所得结果的差异，并与IGS发布的参考值进行比较，证实此方法测量精度较高，且有较好的可行性。

GNSS接收机；天线相位中心；倾斜测量

0　引言

全球导航卫星系统（global navigation satellite system，GNSS）作为一种高效的测量技术手段，因具有测站点间无需通视、全天候观测、测量范围大等特点，广泛应用于测绘、国土、建筑工程、地球物理和地质灾害监测等领域。GNSS水平方向测量精度较高，垂直方向测量精度相对较差。其中接收机天线相位中心垂向偏差是影响高程测量的因素之一，其偏差最大可达数厘米[1-2]，这对精度要求较高的变形监测、GNSS水准测量而言不容忽视。

目前，常见的相位中心检测方法为我国测绘行业检定规程CH8016—95和国家校准规范JJF1118—2004中规定的旋转天线法，即在野外基线检测场上，通过解算基线的较差来测定相位中心，该方法只能有效检测天线相位中心垂向偏差的水平分量，而垂直分量无法检出[3]；高差比较法配合精密水准仪可求得待测天线的垂向偏差；交换天线法需要配合检测的另一个天线垂向偏差必须已知，否则求出的只是2个天线的相对垂向偏差[4-5]。

本文利用卧轴多齿分度台提供的标准角，在1个垂直面对接收机天线进行多角度的倾斜状态观测，配合另外4台接收机进行静态相对定位，其他天线无需已知垂向偏差，就可解算求得待测天线绝对的垂向偏差。

1　检测方法

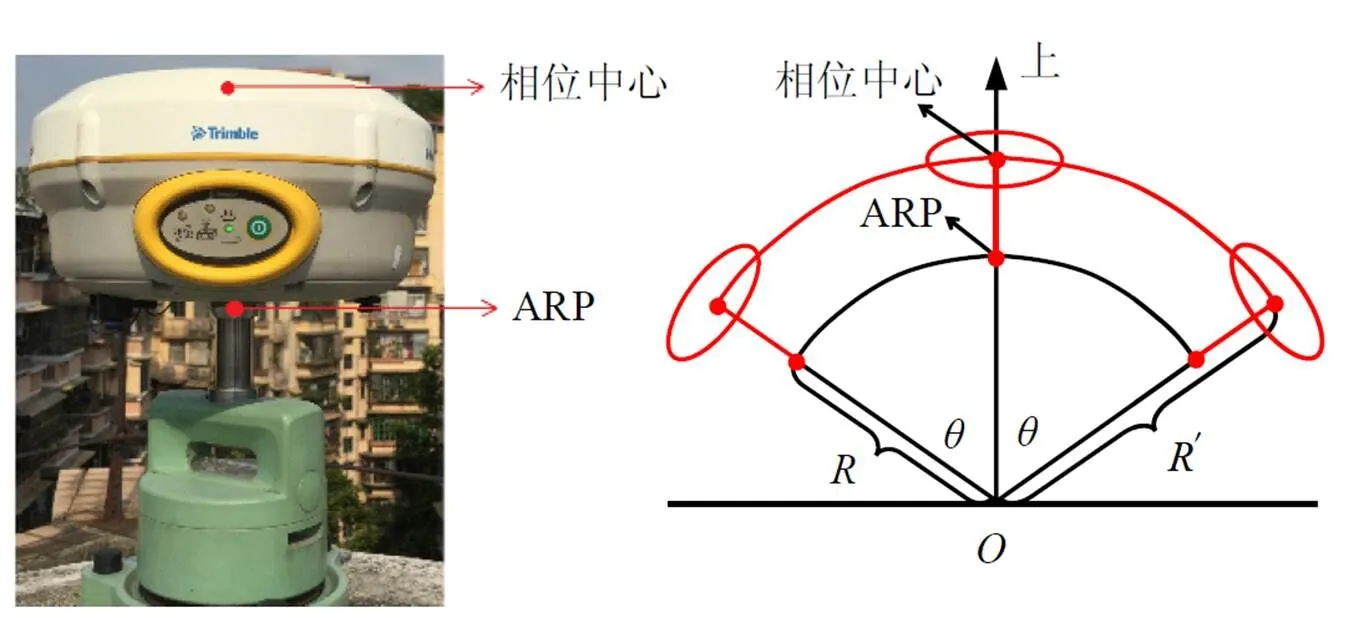
图1　 垂向偏差检测原理

2 检测与试验

在本院楼顶GNSS接收机超短基线场进行检测实验（见图2），基线长3 m ~7 m，视野开阔、无干扰。将卧轴多齿分度台（最大分度间隔误差小于0.5″）置于基线场中心点观测墩GA5，调平固定并锁紧。用数显卡尺（最大允许误差为±0.04 mm）测得测量杆顶端到齿台中心距离为238.2 mm。接收机选用5台Leica GS15，待测接收机天线安置在多齿分度台的测量杆上，其余4台接收机分别安置在周围点位GW1，GW3，GW5，GW7进行同步静态观测。多齿台每倾斜旋转一个角，观测一个时段（时长约1 h，采样率10 s，截止高度角15°）。解算基线网并固定某个配合点做约束平差[6]，求得待测天线每个角时的基线向量（即坐标差），可认为是天线的三维坐标。

3　数据处理及结果分析

经过解算求得各个点坐标及角度信息如表1所示。试验中所用多齿台为552齿，1格为（360/552）°，其中倾斜角为0时，天线处于垂直状态，左右倾斜±15格、±30格……为倾斜状态。解算结果为1频率下的固定解。

图2 　实地试验

3.1　利用点三维坐标直接拟合半径

根据表1这些点的三维坐标，依据最小二乘法在空间拟合一个圆弧，求出圆的半径。

空间圆实际上是空间圆球与空间平面的交线。因此先进行空间平面最小二乘拟合，再拟合空间圆球约束于此平面。设点位坐标为（x,y, z）（=1,2,…,），平面方程可表示为

将观测坐标代入式(1)，可得到

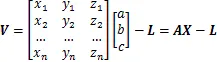
空间圆球的方程可表示为

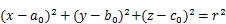
将观测值代入式(3)，并线性化展开可得误差方程为

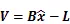
其中

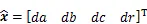
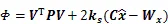
根据附有条件的间接平差法，可得法方程为

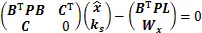
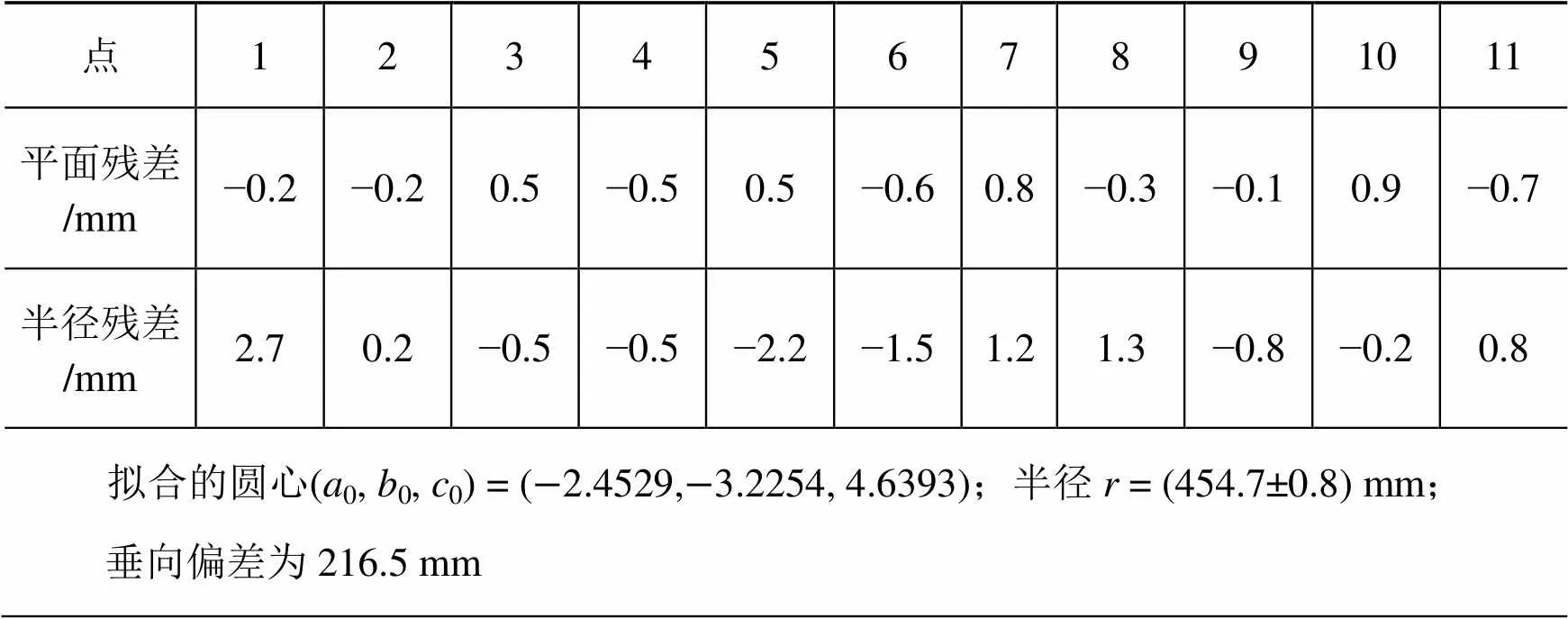
表2　 直接拟合结果及残差

在国际GNSS服务组织IGS发布的天线文件[9]，查询Leica GS15型号接收机的天线1频率相位垂向偏差为202.05 mm，计算结果与其相差14.4 mm，以GNSS测量精度，不应出现如此大的差异。

3.2　 利用弦长计算半径

考虑到GNSS接收机水平方向和垂直方向的测量精度不一致，因此，这些三维坐标的水平精度优于垂直精度。而且在直接拟合中舍弃了多齿台标准的角度信息，故根据几何关系采用测量精度最高的水平弦长直接求半径的方式更为合理。由左右对称分布的2测量点坐标计算其弦长为

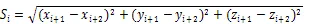
其中=1,3,5,7,9,…

由图1可知，两侧相位中心点和点组成等腰三角形结构，圆心夹角为2，由余弦公式计算半径为

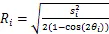
其中=1,3,5,7,9,…

由对称分布的10个点得到5条水平弦长，计算半径求平均值及其残差如表3所示。

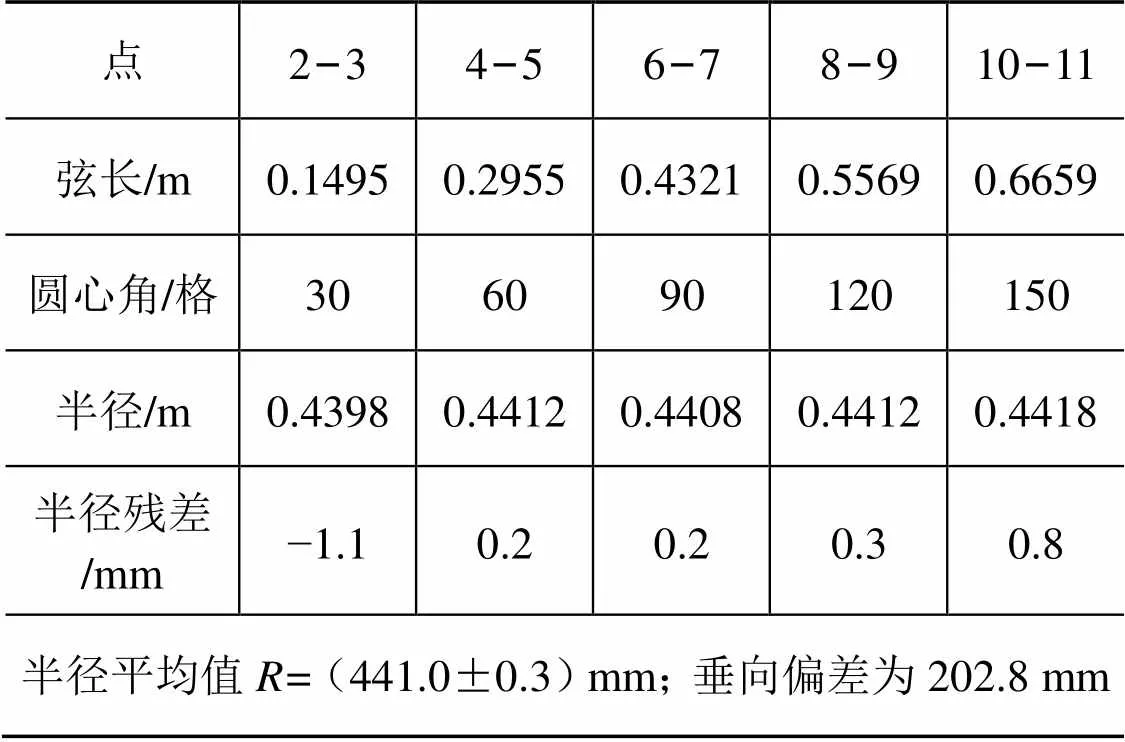
表3 　由弦长拟合结果及残差

由表2和表3可以发现，2种计算方法得出的半径结果分别为454.7 mm和441.0 mm，差异较大；同时发现采用三维坐标直接拟合半径残差较大，但由精度最高的水平弦长计算半径的残差小了许多，结果与参考值差异小于1 mm，因此第二种计算方法更可靠。

为进一步确认，用同样的方法测试Leica AX1202天线和Trimble ZEPHYR天线，用弦长计算半径得到垂向偏差结果分别为65.2 mm和55.9 mm，与IGS给出的参考值差异均小于2 mm。

4 　结语

针对GNSS接收机天线相位中心垂向偏差，进行了倾斜测量试验，通过不同的数据处理算法，发现GNSS水平和垂直方向测量精度不一致对拟合结果影响较大。试验表明：采用精度较高水平方向弦长数据能较好地算出旋转半径，根据几何关系进而得到天线垂向偏差；且本方法不需要已知的天线相位信息，解算结果与IGS发布的参考值很接近，证实了本方法的正确性和可行性。该方法可用于实际高精度GNSS校准中，以进一步提高定位精度。本文研究处于初步阶段，下一步将进行多种型号不同频率下的试验。

[1] Mader G L. GPS antenna calibration at the national geodetic survey[J].GPS Solutions,1999,3(1):50-58.

[2] 张磊,兰孝奇,房成贺,等.天线相位中心改正对GPS精密单点定位的影响[J].测绘工程,2018,27(3):35-38,45.

[3] 张润涛,马德强.利用室外旋转天线法估计导航卫星接收机天线相位中心偏差[J].全球定位系统,2016,41(4):17-21.

[4] 郭金运,徐泮林,曲国庆.GPS接收机天线相位中心偏差的三维检定研究[J].武汉大学学报(信息科学版),2003,28(4): 448-451.

[5] 徐绍铨,高伟,耿涛,等.GPS天线相位中心垂直方向偏差的研究[J].铁道勘察,2004(3):6-8.

[6] 李征航,黄劲松.GPS测量与数据处理[M].武汉:武汉大学出版社,2005,182-201.

[7] 武汉大学测绘学院测量平差学科组.误差理论与测量平差基础[M].武汉:武汉大学出版社,2003.

[8] 李旭.空间圆拟合方法在地铁洞门坐标计算中的应用[J].测绘与空间地理信息,2015,38(3):177-178,181.

[9] Ralf Schmid.Satellite/Receiver antenna corrections [DB/OL]. (2015-11-02) [2018-12-02]. http://acc.igs.org/antennas/igs05_ igs08_test.atx.

Vertical Deviation Detection of Antenna Phase Center in GNSS Receiver

Zhou Guangyong1,2Yu Qingbin1

(1.Guangdong Institute of Metrology 2.Guangdong Provincial Key Laboratory of Modern Geometric and Mechanical Metrology Technology)

On the basis of the relative positioning method，a new method is proposed to calibration the vertical offset of the antenna phase center. Field Tests were carried out. A Precise Angle Dividing Table with horizontal axis provides a standard angle to measure antenna tilted angles, with the remaining four receivers logging static observations simultaneously and finally get the coordinates of the antenna under test to fix the offset, then analyzed the different data processing methods and its differences, and compared with the IGS reference value, confirmed that this method has high accuracy and good practicability.

GNSS Receiver; Antenna Phase Center; Tilt Measurement

周广勇，男，1984年生，硕士，高级工程师，主要研究方向：测绘仪器计量检测。E-mail: zhougygz@126.com