CLM相继故障模型在正常人静息态fMRI脑网络上的研究

柯　铭　曹　黎

(兰州理工大学计算机与通信学院　甘肃 兰州 730050)

0　引　言

复杂网络理论以Watts和Strogatz关于小世界网络[1]，以及Barabasi和Albert关于无标度网络[2]的开创性工作之后，已经发展成为一个多学科交叉研究的前沿。复杂网络结合脑的研究已经成为脑科学领域研究的热点。最早，Stam[3]利用5个健康被试在无任务条件下的脑磁图数据，建立了人脑功能网络并研究了不同频率段下构建的脑网络的网络属性。随后，Salvador等[4-6]进行了一系列基于fMRI数据构造的复杂网络分析，其研究的主要结果为：进行了静息态fMRI的频率域分析，发现两两脑区之间的部分相干谱取决于脑区间的解剖距离；发现静息态fMRI的低频条件下的脑网络具有“小世界”属性；构建了老年与青年的静息态fMRI的脑网络，发现两个网络均呈现“小世界”属性以及较高的全局效率和局部效率等结果。Basset等[7]综述了近些年该领域的发现并指出“小世界”是适应性复杂动力学问题的一个解决方案。同时，王艳群等[8]构建了正常人的fMRI脑功能网络，验证了其具有模块化结构。复杂网络结合脑的研究同样被应用到了疾病的研究。李越等[9]分析了抑郁症患者脑网络社团结构的改变，为该疾病提供了重要的应用与临床诊断价值。Pedersen等[10]发现癫痫患者脑网络的节点以更离散化的方式变化可能与该疾病相关。

目前，基于fMRI构建的复杂脑网络旨在研究初始网络的静态拓扑属性等指标。如上文所述的研究成果等，学者们较多关注的是节点并未遭到攻击时的理想状态下，脑网络的各项网络拓扑属性。但脑网络是一个高效的动态的网络[7]，某个节点的失效可能会引发灾难性的后果。尤其负荷最大节点的失效，其承载的信息量将瞬间崩溃，对整个脑网络的鲁棒性将会产生的影响尚不清楚。从保护脑网络整体性角度，我们认为研究脑网络负荷最大节点失效引起的动态变化极其重要。因此，本文引入一种相继故障模型来研究网络中负荷最大节点失效所引起整个网络的动态变化。

相继故障是指在大部分实际网络中，一个或多个节点的失效(随机或蓄意)会通过节点之间的耦合关系引起其他节点发生故障，由此产生连锁反应，导致相当一部分节点甚至整个网络的崩溃。CLM相继故障模型[11]为负荷-容量模型中的一种子模型，亦称为节点与边混合动态模型。在该模型下，节点过载不是简单地移除，而是降低该节点与其他节点之间的连接效率，与脑网络较为符合。Kinney等[12]曾将CLM相继故障模型应用到北美电力网络。发现攻击负荷最大的发电节点或者输电节点时，网络的整体性能相对于正常状态下有所下降，且随着容量系数的减小，网络的平均效率亦下降。

本文首次将CLM相继故障模型应用到正常人脑进行研究。我们旨在关注正常人脑网络在节点失效后网络拓扑结构的变化，探索网络效率的改变，以此研究正常人脑网络的鲁棒性与脆弱性，具有创新意义。首先对正常人的静息态功能核磁共振图像进行预处理，利用AAL模板将正常人的大脑分割成90个脑区。然后分别计算两两脑区之间的Pearson相关系数。接着设定阈值以获得邻接矩阵来描述脑功能网络。最后设置容量系数，赋予该网络每个脑区容许值。并对负荷最大脑区进行攻击，分析人脑功能网络的鲁棒性与脆弱性。

1　方　法

1.1　被　试

采用18例正常人的核磁共振(fMRI)图像作为被试。其中，7例男性，11例女性，年龄在10～34岁之间，平均年龄19.9岁，且均为右利手。该数据是在Siemens Magnetom Trio 3.0T超导MR仪上进行静息态功能磁共振数据采集。采用梯度回波-平面回波成像GRE-EPI(gradient echo-echo planar imaging)序列进行扫描，扫描范围包括全脑，基线平行于前后联合，扫描参数如下：TR 2 000 ms，TE 30 ms，层厚3.8 mm，层间距0.38 mm，层数34，FOV 240×240 mm ，矩阵64×64，反转角90°，共采集200个时间点，扫描时间6 min 40 s 。要求受试者平卧，头部固定，闭目，塞耳，尽量不做意向性思维。

1.2　数据预处理

在matlab环境下利用DPARSF和rest软件对数据进行处理。其中，DPARSF进行的处理步骤包括：DICOM数据的格式转换、去除前10个时间点、头动校正(平动1 mm，旋转1度)、空间标准化、平滑、去线性漂移、低频滤波。利用rest提取协变量、再去除协变量。其中，协变量定义的是灰质、白质和脑脊液。

1.3　功能连接

脑区间的时间序列同步性可表示脑区间的功能关系。功能连接关系主要由Pearson相关系数[13]表示。本文Pearson相关系数旨在计算两两脑区间的时间相关性，以此表达功能连接关系。由此，采用rest软件做功能连接。首先，利用AAL模板(共90个脑区)定义ROI，将大脑分割成90个节点，并提取90个节点的时间序列。然后，利用rest软件的“ROI-wise”功能，计算90个脑区间的Pearson相关系数，可得一90维对称矩阵，值均在-1～1之间且包括端点值。该矩阵即表示所有脑区之间的Pearson相关系数。Pearson相关系数的计算公式为：

(1)

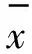
1.4　脑网络构建

由功能连接，得到每个被试90个脑区两两之间的Pearson相关系数矩阵。首先，Z值化每个被试该相关系数矩阵，使其满足正态性。然后，将所有被试的相关系数矩阵求和并均值化，得到一个表示所有被试的相关系数矩阵。最后，构建二值网络时，为消除由噪声引起的弱连接，需设置阈值a(a>0)将连接强度偏弱的值删除。若相关系数矩阵中的值大于等于a或小于等于-a，则表示该两脑区存在连接，即设置为1，否则设为0。邻接矩阵中对角线的元素设置为0，以避免自连。据文献[6]报导，脑网络是一个复杂且稀疏的以大量短程边为主的网络。同时，为保证脑网络的连通性，认为脑网络中没有孤立的节点[14]。因此，本文构建脑网络时，所设阈值对应的邻接矩阵的平均度(K)必须大于2ln90且网络密度在10%～50%之间[14]。其中，网络密度m为：

(2)

式中：N为网络节点数；Ki为节点i的度数。根据以上规则，可得到描述脑网络的邻接矩阵。接着，再根据CLM相继故障模型，对所构建的脑网络进行模拟攻击。

1.5　CLM相继故障模型

CLM相继故障模型由一般的无向无权图G来表示传输网络，各个节点i、j之间的边权值eij∈[0,1]。eij表示该条边上的传递效率。N×N的关联矩阵{dij}代表了最短路径值矩阵；N×N的关联矩阵{eij}代表了节点之间的效率值矩阵。节点t时刻的负荷定义为：该时刻经过该节点效率(距离)最优(短)路径的条数(该模型默认信息通过最短路径传递)，其中负荷用Li(0)表示。效率最优路径定义为，对节点对(i，j)之间的所有路径，计算该时刻效率值之和的最大值。同理，i、j两点间最短路径定义为，该时刻距离之和最小值。效率定义为：εij=1/dij，节点负荷容许值为：Ci=a×Li(0)(a≥1)，其中a代表容量参数。该模型用平均效率来表示整个系统的传输机制，即：

(3)

假设在t=0时刻，网络G的传输效率值矩阵为{eij}，每个节点均有一个初始负荷。当对某个节点进行攻击(在该模型下，攻击某个节点亦为移除某个节点)时，必然会导致网络G的效率最优路径改变，从而导致节点的负荷重新分配。可能引发节点过载，便会引起新一轮的负荷重新分配，最终可能导致相继故障的发生。只有当每一次重新分配的负荷均小于对应节点的初始容量，该相继故障才会停止。其中定义节点间的效率eij的演化公式为：

(4)

1.6　网络特征分析

脑网络经CLM相继故障模型攻击后，其拓扑结构发生变化，全局效率与局部效率对网络的拓扑结构具有重要描述意义。如下，重点描述全局效率与局部效率(整个网络)以及某个节点的局部效率。全局效率定义为：

(5)

局部效率定义为：

(6)

式中：N表示网络节点数，E(Gi)表示第i个节点的局部效率。E(Gi)定义为：第i个节点的所有邻居节点间的效率均值。因此，整个网络的局部效率为N个节点局部效率的均值。

2　结　果

2.1　构建脑网络结果

本文阈值的设置从0.2开始，依次增加0.01，计算出不同阈值下对应的平均度。同时，必须满足每个阈值对应的平均度(K)大于2ln90且不存在孤立节点。平均度与阈值关系如图1所示，横轴r表示阈值，纵轴K表示平均度值。随着阈值增大，平均度逐渐减小，在阈值>0.31时，脑网络开始出现孤立节点。同时，阈值为0.3时的平均度与网络密度分别为14.69与16.5%，满足平均度大于2ln90与网络密度在10%～50%的条件。本文取阈值为0.3构造复杂脑网络。由此，得到一个无权无相的邻接矩阵，即表示构造的脑网络模型。

图1　阈值与平均度关系图

2.2　负荷最大节点攻击结果

负荷最大节点表示在t时刻最短路径经过该节点的次数最多。由于此节点的网络拓扑较丰富，且具有高于全脑水平的局部效率，该节点对于整个网络具有重要意义。本文构建的脑网络中，负荷最大节点对应的脑区为左侧眶内额上回。

在不同容量系数下，对负荷最大的脑区进行攻击，分析攻击该节点之后的平均效率、整个网络的局部效率、负荷最大节点的局部效率，得到图2中所示的三条曲线。

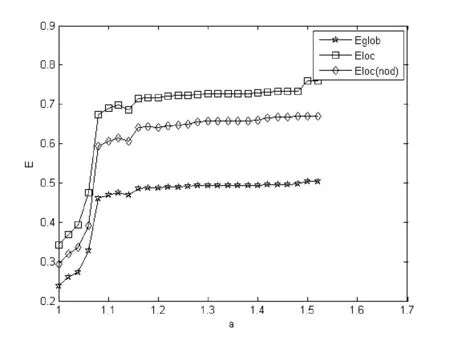
图2　不同容量系数下攻击得到的全局效率、局部效率(整体、单个节点)变化趋势

在图2中，横轴的a代表阈值，纵轴的E、表示效率值。其中，Eglob、Eloc、Eloc(nod)分别表示全局效率、整个网络的局部效率、攻击之后负荷最大节点的局部效率。三条曲线随着容量系数a的增加几乎均逐渐增加，且均逐渐逼近各自的初始效率(攻击该节点后，网络拓扑结构没有发生改变时的效率)。同时，发现攻击之后得到的全局效率、整个网络的局部效率与负荷最大节点的局部效率在不同容量系数下依然具有较大值。在不同容量系数下，整个网络的局部效率值高于全局效率值。且负荷最大节点的局部效率值在不同容量系数下高于全局效率值但小于整个网络的局部效率值。

全局效率聚焦于整个网络拓扑结构的变化，图2中全局效率的变化趋势显示，容量系数与全局效率呈正相关。随着容量系数递增，脑网络的全局效率越接近初始全局效率(0.503 1)。经计算，当容量系数为1时，该脑网络的全局效率较初始全局效率值降低52.6%。同时，发现容量系数为1.06时，该大脑全局效率较初始全局率值仅降低了8%，同比容量系数为1的大脑遭遇攻击时的全局效率竟提高了93.7%。

3　讨　论

攻击结束之后，具有较高的全局效率与局部效率表明，整个脑网络节点之间的信息交互在整个网络与局部间具有较好的平衡。同时表明，脑网络是一个具有较稳定拓扑结构以及高效性能的网络。该结论与Salvador等[15]的研究结果吻合。攻击之后，整个网络具有较高的局部效率表明正常人的脑网络具有较好的容错性[16]。结果中，全局效率在不同容量系数下均具有较高的效率值，表明脑网络在全局网络层面表现出较强的鲁棒性。综上所述，脑网络对于抵抗相继故障表现出较强的鲁棒性且该网络具有较稳定的拓扑结构。对于整个脑网络的局部效率高于全局效率的结果，表明局部节点间的路径(效率)较短(较优)，在局部节点间的效率传递自然较高。但整个网络间相对于局部节点间的路径就变得较长，造成全局效率低于局部效率。进一步证明了脑网络确实是一个稀疏且以大量短程边为主的网络[6]。同时，结果显示攻击结束后，新的负荷最大节点的局部效率低于整个网络的局部效率。与初始网络中负荷最大节点的局部效率高于整个网络的局部效率截然相反。由此表明，攻击该节点对于脑网络的正常拓扑结构确实产生了一定的破坏，使脑网络拓扑结构产生了较大的变化。提示，脑网络虽具有较强鲁棒性，但需注意保护脑网络中负荷最大的节点，以维持较正常的拓扑结构。

此外，结果显示，脑网络中容量系数对于提升全局效率的效果显著。表明，容量系数增强脑网络的鲁棒性。该结果与Kinney等[12]研究北美电力网络时，发现容量系数对于平均效率的作用趋于一致。同时，Crucitti等[11]认为，容量系数相当于对一个复杂网络进行“保护”，这种保护机制可以看作是相继故障被系统本身“容纳”和“吸收”了。从该相继故障模型的角度，进一步分析容量系数的这种“容纳”和“保护”机制。发现，每个节点均对应一个负荷，再乘以容量系数即是初始容量。因此，增加容量系数亦增加了该网络的容负荷能力。而负荷是由经过该节点的所有最短路径次数决定。显然，增大容量系数相当于缩短了该节点到达其他节点间的最短距离。这种距离的缩短可通过增加网络冗余容量来实现。由此，增大容量系数，即增加网络冗余容量，从而增强网络的鲁棒性。综上可知，增加网络冗余容量是一种抵抗相继故障的有效手段。该结论与徐野等[17]发现小世界网络的网络冗余越大，其鲁棒性越强的结论基本一致。因此，间接增加的网络冗余容量才是“容纳”和“吸收”机制的根源。不失一般性，增加脑区之间的冗余容量，复杂脑网络的鲁棒性必然增强。由脑区间功能连接强度来构造网络可知，网络冗余与功能连接强度成呈正相关。即增强某些脑区间的连接强度必然增强脑网络的鲁棒性。该研究结果可为脑网络连接异常的疾病治疗提供参考。

4　结　语

本文首次将CLM相继故障模型应用到正常人脑网络，该模型与脑网络降低脑区间效率的方式较符合。利用Pearson相关系数构建脑网络，分析它的功能连接水平并对其进行攻击。本文发现，基于负荷最大攻击策略下，脑网络的鲁棒性随着容量系数的增大而增强。

对脑网络的网络拓扑属性进行分析，发现脑网络冗余越多，脑网络鲁棒性越强。提示增强脑区间的功能连接强度，可增强整个脑网络的鲁棒性。该结果为相关脑连接异常的疾病提供了治疗参考。同时，发现整个脑网络具有稳定的拓扑结构以及较强鲁棒性。并且提示注意保护脑网络中负荷最大节点。

本文也存在诸多不足。比如，正常人样本量较少。构建复杂脑网络时，90个节点过于粗糙。未来的研究可从细分脑网络节点着手研究。同时，本文构建的复杂脑网络为无相无权图。未来的研究可构建无相有权图，使功能连接的划分层次更精细。CLM相继故障模型，在正常人脑网络上的研究还需进一步推进。

[1] Watts D J,Strogatz S H.Collective dynamics of ‘small-world’ networks[J].Nature,1998,393(6684):440-442.

[2] Barabasi A L,Albert R.Emergence of scaling in random networks[J].Science,1999,286(5439):509-512.

[3] Stam C J.Functional connectivity patterns of human magnetoencephalographic recordings:a ‘small-world’ network?[J].Neuroscience Letters,2004,355(1):25-28.

[4] Salvador R,Suckling J,Schwarzbauer C,et al.Undirected graphs of frequency-dependent functional connectivity in whole brain networks[J].Philosophical Transactions of the Royal Society B Biological Sciences,2005,360(1457):937-946.

[5] Achard S,Salvador R,Whitcher B,et al.A resilient,low-frequency,small-world human brain functional network with highly connected association cortical hubs[J].Journal of Neuroscience,2006,26(1):63-72.

[6] Achard S,Bullmore E.Efficiency and cost of economical brain functional networks[J].PLoS Comput Biol,2007,3(2):17.

[7] Bassett D S,Bullmore E.Small-world brain networks[J].Neuroscientist,2006,12(6):512-523.

[8] 王艳群,李海芳,郭浩,等.静息态脑功能网络的社团结构研究[J].计算机应用,2012,32(7):2044-2048.

[9] 李越,郭浩,陈俊杰,等.抑郁症功能脑网络社团结构差异分析研究[J].计算机应用与软件,2013,30(7):46-50.

[10] Pedersen M,Omidvarnia A H,Walz J M,et al.Increased segregation of brain networks in focal epilepsy:An fMRI graph theory finding[J].Neuroimage Clinical,2014,8(1):536-542.

[11] Crucitti P,Latora V,Marchiori M.Model for cascading failures in complex networks[J].Physical Review E Statistical Nonlinear & Soft Matter Physics,2004,69(4 Pt 2):045104.

[12] Kinney R,Crucitti P,Albert R,et al.Modeling cascading failur es in the North American power grid[J].The European Physical Journal B,2005,46(1):101-107.

[13] Song X W,Dong Z Y,Long X Y,et al.REST:A Toolkit for Resting-State Functional Magnetic Resonance Imaging Data Processing[J].Plos One,2011,6(9):e25031.

[14] 薛绍伟,唐一源,李健,等.一种基于fMRI数据的脑功能网络构建方法[J].计算机应用研究,2010,27(11):4055-4057.

[15] Salvador R,Suckling J,Coleman M R,et al.Neurophysiological architecture of functional magnetic resonance images of human brain[J].Cerebral Cortex,2005,15(9):1332-1342.

[16] Sivan E,Parnas H,Dolev D.Fault tolerance in the cardiac ganglion of the lobster[J].Biological Cybernetics,1999,81(1):11-23.

[17] 徐野,王瑶.复杂网络相继故障的节点动态分析[J].沈阳理工大学学报,2015,34(1):17-21.