隐马尔可夫模型路网匹配的MapReduce实现
陆 健 王 鹏
(复旦大学计算机科学技术学院 上海 200433)
0 引 言
随着科技发展,传感器尤其是位置传感器已经可以出现在几乎所有的可移动设备上。现在市面上的大部分家用汽车几乎都装载有GPS导航器,通过GPS,人们可以相对准确地了解自己所处的位置,导航软件基于此给予司机最优的道路选择。
GPS就是将物体当前在地球上的坐标(对于地面上的物体来说,即为二维经纬度坐标)测量出来。对于在道路中通行的汽车来说,尤其在路网密集的城市地区,一个二维坐标具体在城市的哪条道路上至关重要,在距离很小的范围内的不同道路能通达的方向可能完全不同。将GPS数据映射到一个更为准确合理的道路上去是大部分基于轨迹信息计算的一个基础。这也就是常说的路网匹配算法。路网匹配算法可以分为两个大类——增量算法和全局算法。前者对每一个新读到的轨迹点坐标立即产生一个匹配结果,不考虑后续的轨迹点数据,后者则对整个轨迹数据进行整合分析。前者更好地处理日常类似汽车导航的实时应用,如果对准确性要求更高,则一般考虑使用全局算法。
城市规模的扩大及新型交通模式,网约车的诞生,手机地图交通类APP的普及,乃至呼之欲出的自动驾驶汽车,定位和导航需求变得越来越集中化,为数据的大规模集中提供可能的同时,也对研究城市的路网规划,或者道路拥挤情况的调查带来了便利,这种研究会获得数量巨大的轨迹数据。类似这些对于大规模轨迹数据的路网匹配工作,实时性不是一个重要的考量,效率和准确性是这种离线路网匹配场景更要考虑的问题。在这种情况下要优先地考虑准确性更好的全局算法。我们称呼这种已经获得轨迹完整数据的路网匹配工作为离线路网匹配。
并行计算框架的使用可以提高大规模数据计算的效率并节约编码成本。现时已经有一些研究着力于使用MapReduce框架来实现大规模轨迹数据的离线路网匹配,使用分而治之的思想简化计算的同时,减少对其他资源的使用,减少I/O开销。但全局路网匹配算法顾名思义是要通过全局考量整个轨迹,这与MapReduce分而治之是一个根本性的矛盾。另一方面,由于地区的不同、路网的密集程度、汽车的使用量不论在世界的哪一国家都有着明显的差异,对于MapReduce框架来说,基于地理位置的分而治之很容易造成工作流和I/O流的不平衡问题,这对计算效率有着很大的问题。这些问题都使得继续对使用分布式计算框架进行离线路网匹配的讨论变的很有意义。
本文为了克服前述两种需求的潜在矛盾,提出了全新的基于MapReduce和隐马尔可夫模型的路网匹配框架。主体包括:
(1) 分布式计算隐马尔可夫模型的框架分布式路网匹配和传统全局匹配相比主要的缺陷是分而治之和全局最优求解的矛盾。将轨迹按照地理位置排序的结果是将轨迹打碎丢失前后连接信息。本研究将轨迹拆分为一段段长度限定的线段,将分布式处理的线段在最后整合起来,得到全局最优解。而这都基于路网匹配的隐马尔可夫模型。隐马尔可夫模型是路网匹配工作中非常流行的全局算法,它有着直观准确且抗噪声能力强大的特点。我们的研究通过将这个算法实现在MapReduce上来实现分布式计算和全局算法的平衡。
(2) 大规模地图数据的分组预处理系统当要让路网匹配在一个较大的地图空间内运行时(如全中国),对于地图文件的预处理并不是一件容易的事情。基于地理位置的正方形分区是极为常用的地图文件组织形式,但在正方形边长和文件数量上有着难以调和的矛盾,进一步将地图分区按照地理位置分组会带来文件I/O和匹配操作负载不均衡的问题。我们提出了一个新的大规模地图数据分组预处理系统,通过地图冗余、随机分组和缓冲区的应用,将混杂的地图数据进行分区分组,保证匹配的正确性和负载均衡。
1 背景知识
1.1 已有的路网匹配算法
大多数现存的路网匹配算法使用各种权值算法从候选点中决定正确的位置[1-3]。权值可以由很多信息来决定,比如GPS信号到候选点的距离,当前的前进方向,道路的拓扑结构,物体的瞬时矢量速度以及前序后续的GPS信号。虽然有的轨迹数据可以在GPS信号以外提供前述的其他信息,但为了满足算法的通用性,包括我们的研究在内,大部分研究都集中于仅有时间和GPS信号的轨迹数据。
权值算法主要分为两类:增量算法和全局算法。增量算法例如文献[4]和文献[5],它们每次读入一个最新的轨迹数据,根据且只根据包括这个新输入在内的所有已知轨迹点来确定新数据对应所有候选点的权值。增量算法由于可以实时地给出匹配的结果,被广泛地用于实时应用场景,例如汽车导航。但当采样率比较低的时候,匹配准确率下降非常显著,也难以应付城市路网的复杂环境。
全局算法例如文献[6]和文献[7]则将一整段轨迹数据进行整体分析,所以可以将后续数据一并利用来确定每一个点的最佳选择。在不大规模增加时间复杂度的情况下,离线路网匹配使用全局算法又能获得更加准确的匹配结果[8]。
1.2 分布式路网匹配算法
MapReduce是一个运行在集群上的并行,分布式处理和生成大规模数据的计算框架和它的相关实现[9]。在Huang等的研究中,提出了将MapReduce应用到路网匹配的工作当中去[10]。方法是使用两次MapReduce。第一次MapReduce的Map函数读入分布式文件系统中的轨迹数据,将轨迹先拆分成单独的轨迹点对所有的轨迹点定位其所属的地图分区,以地图分区编号作为key输出键值对,这样经过shuffle机制,每个Reduce程序只需读入一次相应的地图文件就可以完成所有来自不同轨迹但同属于一个地图分区的所有点的匹配操作,输出所有在范围内的候选道路。在第二次MapReduce中将属于一个轨迹的所有轨迹点的匹配结果通过shuffle机制重归到一个Reduce程序当中排序并进行最优路径求解。这个框架的确成功地将MapReduce应用到分布式路网匹配上,但由于将轨迹分开匹配,匹配结束后只输出候选道路的编号(或道路名)和匹配距离,道路连通性这一在路网匹配中重要的元素无法被考虑在内。另外,由于地理上的不均衡分布,按照地理位置的分布式计算一定会有负载不均衡的问题。
1.3 基于隐马尔可夫模型的路网匹配
隐马尔可夫模型HMM(Hidden Markov Model)是一个描述一个含有隐含未知参数的马尔可夫过程统计模型,其数学模型由Baum等[11]发展出来。Newson等在文献[12]中提出了将隐马尔可夫模型应用到路网匹配当中去。做法是将轨迹点作为HMM模型的观察集,轨迹点的候选道路投影作为HMM求解的对象——隐状态(实状态)。使用信号误差计算发射概率,用路径差值求解转移概率。隐马尔可夫模型是路网匹配工作中非常流行的全局算法,它有着直观准确且抗噪声能力强大的特点。
定义1轨迹是一个移动的物体在地理空间内移动生成的路径。一般由一连串按照时间排列的点构成。例如:p1,p2,…,pn,其中的每一个点有一组空间坐标(x代表经度,y代表纬度)和时间戳t构成。
T:{p1,p2,…,pn}
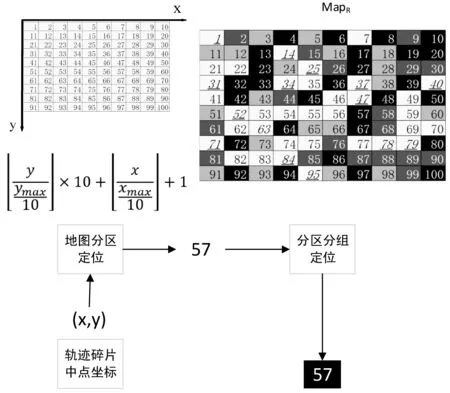
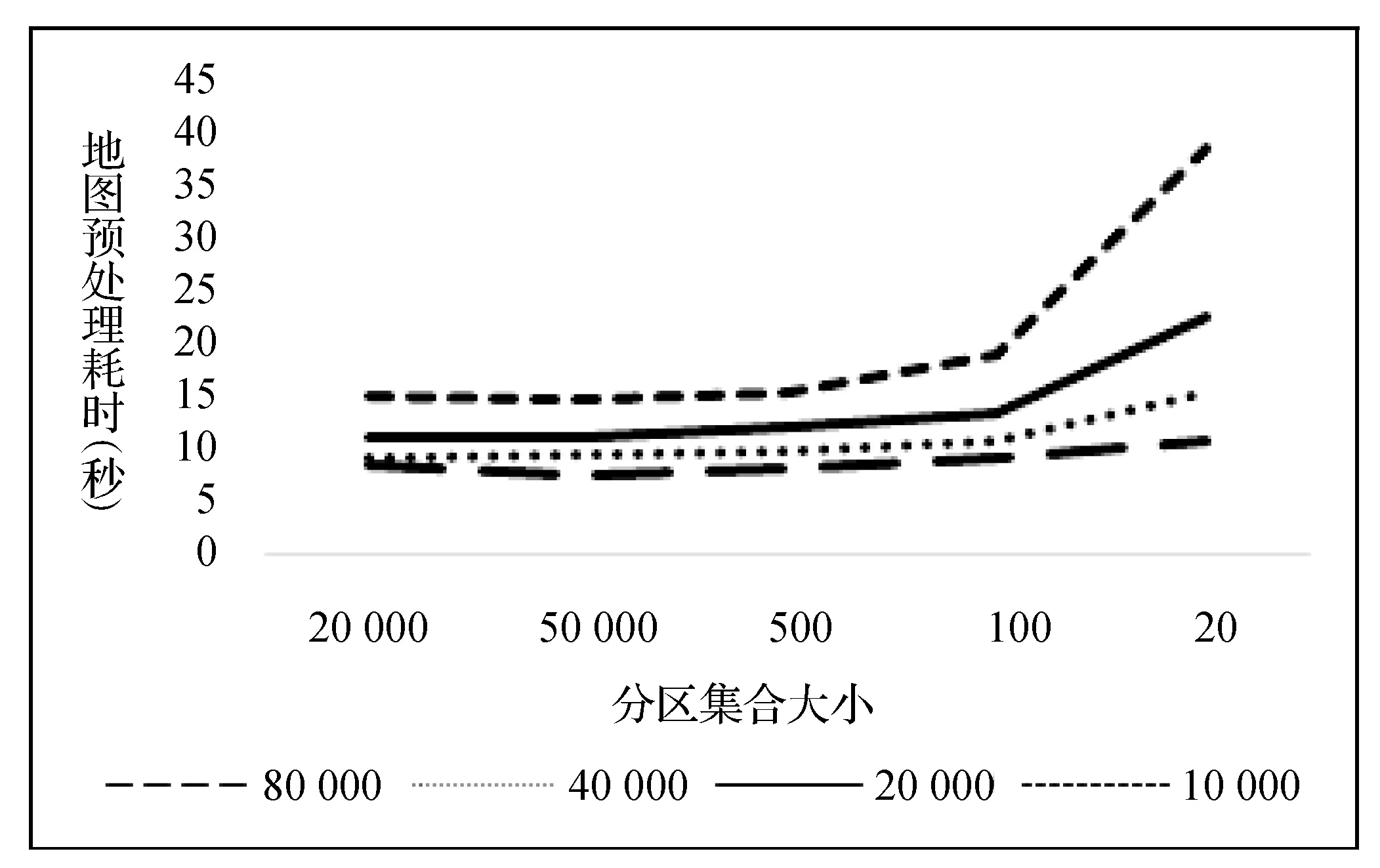
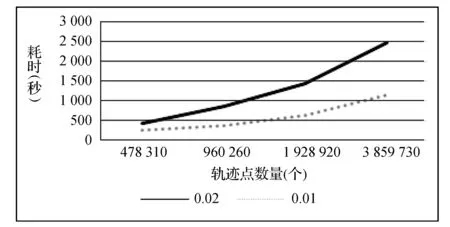
pi=〈xi,yi,ti〉,t1 路网是地图上所有道路的集合,一般用无向图R=〈V,E〉表示。V为路网中由两个端点间的直线段代表的道路集,抑或称作线段集(在下文中,两词意义相同),E是所有直线段的端点集。 定义2路网匹配可以看作一个以轨迹序列为输入和输出的函数。令Tn代表长度为n的轨迹,则定义基于路网R的路网匹配如下: MR为映射: 一般来说,路网匹配的难点是如何选择轨迹点对应的多个候选道路。 定义3点p到道路v的距离D(p,v)是v上任意一点到p的最短距离。 D(p,v)=min(d(p,pv))pv∈v 式中:pv是v上任意一点。d为地图上两点的大圆距离。 定义4点p到道路v的投影Pp,v是v上到p距离最近的点。 一般来说,在路网匹配中,将轨迹点到附近道路的投影作为候选点。使用隐马尔可夫模型求解路网匹配的核心是求解候选道路投影表现出观测轨迹点的发射概率和轨迹点候选的道路投影序列前后的转换概率。前者描述汽车处于某条候选道路上被观测到已知轨迹点的可能性,后者描述汽车在前后两个候选道路间行驶并被观测到已知轨迹序列的可能性。 显然,发射概率反映了轨迹信号的误差,理应随候选道路投影s到观测值o的距离变大而减小。我们假定其概率分布为标准正态分布。 (1) 式中:σ为GPS测量误差的标准差。 (2) 同前作[10]一样,分布式处理的意义仍然是通过拆散轨迹分散到各个地图的块来集中匹配以达到集中匹配减少I/O操作的目的。但将轨迹分而治之的想法与离线路网匹配的最初目标——更高的准确性。因为如前一章所述,将已匹配的点重新聚合在一起无法知道前后两点的候选道路的连通性。而忽略连通性的路网匹配无法应对城市复杂路网。 故我们提出,为了能让轨迹的匹配考虑道路的连通性,在根本上与前作的点匹配不同,我们将轨迹数据进行碎片化,进行段匹配。第一个MapReduce的Map函数不再是简单地将每个轨迹的每个点单独作为value值发射,而是将一对前后连续的轨迹点(pi,pi+1)作为value值发射。 而在之后的Reduce操作中,路网匹配不只是在路网中寻找距离接近的道路作为候选道路记录在匹配结果序列里以待第二次MapReduce整合。对于Map给出的点对(pi,pi+1)不仅要给出这两个点的所有候选道路及其距离(这在隐马尔可夫路网匹配模型里代表了发射概率),还要给出所有前后两个轨迹点在两个候选道路集对应的所有投影点之间的最短路径长度(对应隐马尔可夫模型中的转移概率)。通过这种方式,维特比算法中需要概率模型就被完全计算清楚了。在第二次MapReduce的Reduce中,被排序规整到同一轨迹序列后,就可以执行动态规划算法,计算概率最大的可能路径,给出匹配结果。 实现上一节所述的轨迹段匹配,难度要比以前的点匹配大得多,因为不同于点匹配的对象,段匹配的对象是一对点,必然出现很多时候轨迹的连续两个点事跨越不同的分区边界的情况。而由于我们不仅要匹配轨迹点对应的候选道路,还要在路网中计算候选道路投影间的最短路径。所以,我们要保证一对连续的轨迹点要在同一个地图分区内都被匹配到。当这样的轨迹段的长度有限时,我们可以通过对地图分区做冗余来保证这一点。地图冗余具体来说包括如下的两项: (1) 处于分区边界的道路道路本身可能会贴近边界,那么落在一个分区内的轨迹点很有可能需要跨区域匹配到边界附近的道路,所以将边界附近的道路重复存储显然是必要的。 (2) 长度较长跨网格的道路一些道路本身比较长且道路笔直,在路网中使用较长的线段表示,而且由于正方形分组的顶点位置为四区交界,很容易出现道路跨区域的情况。如果想要匹配能在一个区域内完成就必须要将跨区域的道路重复存储在不同的分区当中。 当要处理的地图规模很大(例如全中国)时,如何用文件保存数量庞大的正方形地图分区会成为一个问题。地图分区的边长基于匹配的需要不能很大,否则分区内道路很多严重影响匹配效率。当地图的数据规模很大时,地图分区的数量很大,所以必然需要将分区进行分组。 而地图数据和轨迹数据基于位置相邻的分组不可避免地会出现偏斜,比如城市拥有更密集的路网,城市有更大的汽车保有量,市中心的道路会比郊区更加拥堵。所以对于按照等面积分区的地图文件组织方式,轨迹的匹配必然会遇到负载不均衡的情况,具体来说,会体现在以下两点: (1) 不同地图分区的I/O效率不同,浪费I/O资源。 (2) 不同地图分区的匹配任务负载不同。 MapReduce任务需要等待最慢的一个Reduce的完成。 而只要地图的划分是基于地理的接近,就没有办法打破这种数据分布的不均。所以,我们提出了将地图按方形切割的前提下将地图分区随机打乱再整合成较大的分组,每个Reduce从对应一个分区到对应一次分组,I/O操作直接调取整个分组内的所有地图分区。 如图1所示,不同的分组由不同的颜色灰度和格子编号字体的不同来区分(前四个分组灰度不同,最后一个使用斜体和下划线)。两个灰色轮廓椭圆为交通流量的密集区域(也同样是路网数据的密集区域),虽然地图被网格等分开来,但相邻的组并不一定要在一个分组内。可以看到右侧的统计,每个分组之内的密集流量匹配区域数量是大体一致的,这种机制不仅让每次I/O获得的地图数据大小基本一致,也让即使偏斜度很大的轨迹数据的计算强度得到了均匀。 图1 地图分区和地图分组 我们之前的讨论都基于一个假设,那就是轨迹的长度都在一个可控的范围之内。根据这种假设,当对地图做切割的方块大小足够大的时候(譬如边长达到2千米),我们可以在其边界上加上一定的冗余,让到正方形中心距离在更大范围内的边也纳入这个分区。 但对于长度较长的轨迹段,长度超过可以接受的范围时,即使地图冗余也终究无法匹配一个越界的轨迹段。所以,我们将轨迹进行插值切割,以分割成长度小于一定阈值的轨迹段。对于长度较大的轨迹段的插值不可避免地会引入误差,毕竟汽车在两个轨迹点之间的运动不必然是接近直线的,但由于: (1) 隐马尔可夫模型是一个对轨迹误差容忍度很高的模型。 (2) 在轨迹数据时间间隔接近不变的前提下,长度较长的轨迹段,往往暗示汽车的行驶速度非常高,也就是说,在这段轨迹中会较少出现曲折。 所以,我们采用了前后两点线性平均分的切割方法,至于采取更复杂的插点分割方法,例如根据前后序列的方向使用曲线拟合插值,或者使用前后方向相交点的插值,我们留作将来继续讨论研究。 综上所述,在这些机制下,我们保证了在将一个轨迹段进行必要的插值切割后,其中的每一个轨迹段,都一定可以在一个正方形网格地图块内完成。 本系统大致分为两个预处理模块和MapReduce模块,如图2所示。一个预处理模块对轨迹数据进行去噪声和轨迹分割,将预处理的数据存于分布式文件系统或者分布式数据库中等待匹配。另一个预处理模块对大规模地图数据的分区分组。对于我们的系统来说,地图预处理使得对于大规模轨迹数据在大规模地图空间下的路网匹配成为可能的同时,确保各个地图分组文件的大小基本一致,匹配的I/O操作负载和计算负载得到均衡。MapReduce的前半模块执行碎片化轨迹和轨迹预匹配过程,也就是对于轨迹进行分而治之,将轨迹打碎后按照地理位置的不同分组,再分配到相应的组内进行路网匹配。后半模块执行第二次MapReduce的汇总和轨迹生成,将匹配到候选道路的轨迹点重新按照轨迹聚集起来,计算最有可能的路网匹配结果。 图2 系统框架 接下来简述整个基于MapReduce和隐马尔可夫模型的路网匹配的工作流程。算法整体分为两个阶段。第一个阶段为数据预处理,在该阶段,我们将地图和轨迹进行预处理。第二个阶段包含两个MapReduce作业,完成对一个批次的轨迹数据的路网匹配。 首先,在系统准备阶段,由地图预处理系统将整个地图数据读入。将路网按照网格存储到不同的分区当中,对于网格的边界和跨越网格的道路,则将它们冗余存放到多个相关分区当中去。随后,将大量的网格随机分组到一个小数量级的分组内,任何一个分区进入任何一个分组的概率都是随机均匀分布。将得到的地图分组以一个文件的形式存储于文件系统中。 轨迹数据首先要经过预处理,首先将轨迹数据以停留点作为中断分割开来,以车牌号连接轨迹开始时间作为数据的主键,以连续的轨迹点坐标作为值存入分布式文件系统或者分布式数据库例如Hbase。在这个工作中,还用了简单的速度规则去除了异常轨迹点。 之后进行MapReduce计算,在第一次MapReduce过程中,Map程序从文件系统中读入网格划分的映射表。从分布式文件系统或者分布式数据库中读取每一条轨迹,以先后顺序扫描轨迹,当前后两点的距离小于阈值时,直接定位前后两个点中点所在的网格编号,在网格划分映射表中找到网格所在的分组号作为键,轨迹段序号和轨迹段本身作为值输出。 在Reduce中,从分布式文件系统中读入键值对应的这个分组下所有分区的地图数据。对于每一段轨迹碎片,读入对应的地图数据进行匹配计算:1) 前后两点所有的路网候选投影;2) 前后两个候选投影集之间的最短路经。以轨迹碎片所在轨迹id为键,以轨迹碎片id,轨迹碎片两端点的所有候选投影和所有转移距离作为值输出。 在第二步MapReduce中,以前一步Reduce的输出作为读入。Map程序不改变键值对的内容。经过shuffle,Reduce程序将键对应的轨迹的碎片段匹配结果汇总起来,通过已经算出的候选路网投影和候选投影间的最短路径计算维特比算法中的转移概率发射概率,最后计算出最可能的路径。 基于正方形网格划分,我们讨论如何保证网格包含所有落在网格内的有限长度的轨迹碎片在原地图数据中匹配到的候选路段。 定义5轨迹碎片 对于轨迹P:{p1,p2,…,pn} 轨迹碎片segi=(pi,pi+1),1≤i≤n-1,pi,pi+1分别是轨迹碎片的两个端点。对于轨迹碎片的两个端点,它们在临近道路上的投影是路网匹配结果的候选项,也就是隐马尔可夫模型里的隐状态。 定义6线段距离和线段投影 对于点p和线段v的线段距离: 即线段距离点p到线段v任意一点的最短距离。取到最短距离的点e即为线段投影Proj(p,v)。 如图3所示,点p到线段(也就是道路)v的投影和p点到道路v所在直线投影的区别就是当点p到线v段所在的直线投影不在线段v上时,线段投影会取被投影线段v两个端点中离p更近的作为线段投影的结果。 图3 线段距离和线段投影 对于距离阈值D及地图R=〈V,E〉,定义一个点的候选道路集。 定义7候选道路集:C(p)={v∨d(p,v) D代表了一条道路可能是轨迹点对应的候选道路的最大距离阈值。 定义8对于我们的匹配对象轨迹碎片来说,定义轨迹碎片的候选道路集C(segi)为两个端点候选道路集的并: C(segi)=C(pi)∪C(pi+1) 我们将任意一个正方形地图分区标记为B,对应的分区中心c,正方形边长为α。设有轨迹碎片集合SG,mid(seg)为轨迹片段的中点。 证明:显然,从c到轨迹片段中心,从轨迹片段中心到轨迹端点,从轨迹端点到候选道路的线段投影构成了一条从c到候选道路v的通路,由线段距离的定义,这条通路的长度一定大于等于线段距离。所以由: 得证。 地图分区对地图里的所有道路都要检查其离附近的地图分区中心距离是否小于阈值,临近分区的数量和道路长度成正比,地图大小|R|,道路平均长度为|v|为所以时间复杂度为O(|R||v|)。 为了将读地图的I/O负载和路网匹配的工作负载均匀地分布在集群的机器上,我们将地图分区随机分布到数量级小很多的地图分组里去。实现方法是依编号遍历所有网格,对于给定的地图分组数量N,生成一个1~N-1的随机数k,并将这个网格添加到k号分组Gk之内,并保存这个网格序号到分组序号的映射关系到地图分组映射表MapR之内,映射表对于分区编号的映射结果就是分区所属的分组号,即: 对于地图分组,要将所有地图分区扫描一遍。计算复杂度为O(|grid|),|grid|为分区数量。 第一次MapReduce的Map程序完成对大规模轨迹数据的碎片化并分发到各个Reduce进行路网匹配。 ‖seg‖l~ 段在进行定位。 定位碎片段分为两步,如图4所示。首先计算轨迹碎片中点落于哪个地图网格。计算得到网格编号gridNo后(在图中由数字57表示),再读取之前地图预处理时保存的映射文件MapR(图1),查询到这个网格所处的分组号groupNo=MapR(gridNo)(在图中以分组颜色表示)。对于来自轨迹编号trajNo的第i轨迹碎片segi:(pi,pi+1),使用碎片中点mid(segi)查询到属于网格编号gridNo,和网格所处分组号groupid。Map程序的输出为: Key:groupNo Value:gridNo,trajNo,i,pi,pi+1 图4 碎片段定位 Map程序会将键值相同的键值对集中起来发射出去。而一个Reduce程序收到且只收到所有键值拥有同样的键值对。Reduce根据这个唯一的键也就是一个地图网格组的分组号groupid,从分布式文件系统中读取这个组的地图数据。其中包括所有落在这个组内的所有地图网格。之后对于收到的值序列:gridNo,trajNo,i,pi,pi+1,根据gridNo读出分组GgridNo中在这次匹配中需要利用的地图分组Bgridid。在这个分组中遍历所有的道路,将距离点坐标pi:(xi,yi)和pi+1:(xi+1,yi+1)距离小于距离阈值D的道路v和对应的线段投影Proj(p,v)组成值对:〈v,Proj(p,v)〉,添加到前后两点的候选道路集backCandidate,forwardCandidate。之后依据组内的地图信息和最短路算法计算前后两个候选道路集的线段投影间的最短距离,存入连接结果集合Route,如果在图中没有连接通路,则记录不能连通标志“unlinked”。Route集合显然应该有|backCandidate|×|forwardCandidate|个元素。Reduce的计算结果要作为第二次MapReduce的输入,第二次MapReduce的目标是把轨迹碎片重新拼接起来,所以需要先将同一段轨迹的碎片带着同样的键值被shuffle排序并分发到不同的Reduce。所以第一次Reduce的输出应当如下: Key:trajNo Value:i,pi,pi+1,backCandidate,forwardCandidate,Route 第二次MapReduce将碎片化的轨迹重新规整起来,Map将上一次MapReduce的结果读入并直接输出,shuffle机制将键值相同也就是同一段轨迹的所有碎片聚集到一个Reduce里。 在一个Reduce当中,首先将所有收集到的已匹配碎片进行排序,这里除了轨迹的首尾两点以外,每个轨迹点都会有两个候选道路集,在绝大部分情况下,前后候选集都是一致的,所以可以直接合并。之后对于任意轨迹点的候选集中遍历候选项〈v,Proj(p,v)〗〉,根据式(1)通过候选点v到轨迹点p的距离计算发射概率,再根据式(2)通过Route集合内的最短路径与前后轨迹点之间的距离差值计算转移概率。其次计算维特比算法:先前向计算所有可能通路的最大概率,再根据动态规划的结果反向得到最大概率对应的道路和道路投影的序列。最后要去掉在第一步Map中加入的插值点的匹配结果,输出完整的匹配结果到分布式文件系统或者分布式数据库。 实验在一个包含七台服务器的集群上,每台服务器硬件配置相同,都拥有64 GB内存,CPU为Intel(R) Xeon(R) CPU E5-2403 v2 @ 1.80 GHz。服务器运行Ubuntu系统,版本号为12.04。Java版本为JDK1.8。集群上运行Hadoop2.7.2。 对于分布式计算的测试在整个集群上进行,对于单机版匹配的对比在其中一台服务器上进行。 轨迹数据为一组包含1 402个csv表格文件的轨迹数据,每一个csv表格文件代表一辆汽车在一定时间的行驶记录。这些文件大小不一,文件总大小为41.5 GB。所有的轨迹都在中国境内行驶。 地图数据来自OpenStreetMap的开源地图。分为31个json文件,对应每一个中国大陆省级行政单位。地图文件总共为3.18 GB。 虽然我们讨论过地图预处理阶段对地图进行分区分组的计算复杂度,但事实上预处理阶段大部分的时间开销其实会用在I/O文件的操作上。因为在预处理阶段,由于地图数据很大,而我们需要将地图分区设置得比较小(否则在匹配的过程中每匹配一条道路,相应的一个分区的道路需要被全部遍历来计算点到道路的距离,非常耗费时间),整个地图分区的文件数量就会大得惊人。如表1所示,将整个中国作为地图范围的话,由于分区数量反比于边长的平方,随着分区的边长(以经纬度表示)的减小,分区数量增长地很迅速。0.02的经纬度边长相当于正方形边长大约在2.2千米的分组。 表1 分区边长与分区数量 由于没有办法将所有分区全部存储在内存中进行分组,我们就需要将5.1节获得的所有分区以文件的形式存储下来。而分区数量过多无法用单一文件存储(文件数量和I/O操作太大),我们将序号相连的分区存储到一个分区集合中去作为缓冲,在进行5.2节的地图分组过程中在遍历这些文件来读取地图分区。我们将每个集合包含的分区数量设定为相同,记为F。 另一方面,道路在地图数据中存在的顺序是混乱的,在道路确定分区的过程中要使用缓冲区暂时保留一定的读写任务,使得对于分区集合的一次读写能写入更多的道路,不然,对于分区的集合式文件读写会使得I/O负担加重。以下以只处理河南省的地图为例。我们将正方形分组的经纬度边长固定在0.02。这样,整个河南省地图会产生87 904个地图分区,我们测试不同的分区集合包含分区的数量F和缓冲区Buffer大小(一次读写存储道路的数量)对预处理时间的影响。 如图5测试结果所示,不同的折线代表不同缓冲区大小,横轴代表分区集合大小的变化,纵轴是耗时变化。显然缓冲区越大,折线越处于低位,也就是耗时最短,写入缓冲区一定能使预处理的时间缩短,在内存允许的情况下应尽量加大缓冲区。而分区集合的大小则要更加复杂,显然过小的分区集合使得文件变多,I/O次数比较大,在x轴右侧的耗时随着分区集合大小的缩小快速增长。而分区集合特别大时,文件本身数量已经很少,减少文件数量带来的I/O开销的降低并不明显,由于道路在地图数据中本身有区域的偏斜,可能在一段时间内处理的道路恰巧只在某几个分区集合当中不涉及大部分的文件。也就是说集合分区数量F过大甚至会导致更多不必要地图分区在一个文件I/O中被一并读取,使得时间开销更大,当缓冲区小的情况下这种情况更容易观察到。 图5 地图预处理时间 尽管基于隐马尔可夫模型的路网匹配有着高精度的特征,但是运算速度慢是其一个很根本的特点。以往基于隐马尔可夫模型路网匹配所研究的数据集和地图文件大小都在一个非常小的范围内[12-13]。为了证明我们的实现加快了匹配的效率,我们之后在单台机器上对同样的数据集进行单机版的匹配,并和集群比较效率。 图6展示了在分区边长分别在0.01和0.02经纬度下的匹配时间。可以看到集群的运算耗时大致和输入的轨迹点数量呈正比(这里列举的轨迹点数量分别为随机抽取的0.1%、0.2%、0.4%、0.8%的总轨迹数据,即数据量以2的指数增长)。而根据增长趋势估算,集群的处理数据效率为每秒3 300个数据点。 图6 匹配时间 还可以看到,在地图覆盖范围不变的情况下,分区边长对匹配效率的影响很大。分区边长增大,则分区数量减少,能加快地图预处理速度,但在路网匹配时,需要遍历整个分区的道路来确定候选集合,也就是更大的分区对应更慢的匹配速度。0.01经纬度边长的地图分区匹配效率要比0.02经纬度边长匹配效率平均快上一倍以上。但分区会使得预处理更加困难,占用更多内存,大部分情况下,为了匹配速度的对于大规模轨迹数据匹配的持续获利,属于一次性开销的地图预处理时间的增长是可以接受的。 由于不知道合适的并行度,要估计对等情况下本地隐马尔可夫路网匹配的效率则更加复杂,我们需要对单机先进行并行度负载测试。并行度指在一台机器上运行多少个相同的匹配进程我们要测试并行度在单机上最高可以达到多少。结果如表2所示,第一列表示单台机器上运行的同样的路网匹配进程数量,第二列表示这些进程的平均处理速度,第三列表示在相应的单击并行度下伪集群的整体效率。这里第三列对应于我们7个节点的Hadoop集群,我们模拟一个7个节点的伪集群,效率由单节点效率(也就是并行度乘以单进程平均处理速度)乘以7获得。可以看到,当并行度刚刚增加的时候,单进程处理速度反而会变快,这可能是因为多个进程读写硬盘的过程中会利用到其他进程读写的磁盘缓存,使得整体效率提高。但随着进程进一步增长,系统变得很难处理如此频繁且分布未知的随机文件读写,所以效率并不能随着并行度一直上升。当并行度达到7左右时,2 500轨迹点/秒大约就是效率的顶峰。相比之下,我们可以得出结论,我们的系统在大规模数据上可以给出相比于本地匹配30%~40%的效率提升。 表2 单机版隐马尔可夫匹配效率 负载均衡的情况在图7可以非常直观地看到,最耗时的第一个MapReduce的各个Reducer其中包含基本相等数量的地图分组,地图分组又是基于地图分区随机划分的。所以每个Reducer的负载都比较均衡,没有出现一些Reducer特别快,一些特别滞后的情况。在我们的实验中,Reducer的平均负载标准差仅为5%。 图7 各个Reducer的负载 最后我们测试集群节点数量对计算效率的影响,同样对于0.5%的数据和基于0.01为正方形分组边长的匹配进行测试,然后尝试改变MapReduce节点数量。 如表3所示,随着节点变多,运算时间显著减少,证明了Hadoop集群的易扩展性可以为运算提速提供很大的方便。在三个节点的情况下,等效单机运算效率已经下降到160条记录/秒,而单机版在并发度为7时运算效率都超过350条记录/秒。也就是说,在节点很少的情况,选择使用Hadoop集群运算隐马尔可夫模型并不是一个明智的选择。 表3 节点数量与运算时间 [1] Liu Siyuan, Liu Ce, Luo Qion, et al. Calibrating Large Scale Vehicle Trajectory Data[C]// IEEE, International Conference on Mobile Data Management. IEEE, 2012:222-231. [2] Ghys K, Kuijpers B, Moelans B, et al. Map matching and uncertainty: an algorithm and real-world experiments[C]// ACM Sigspatial International Conference on Advances in Geographic Information Systems. ACM, 2009:468-471. [3] Abdallah F, Nassreddine G, Denoeux T. A Multiple-Hypothesis Map-Matching Method Suitable for Weighted and Box-Shaped State Estimation for Localization[J]. IEEE Transactions on Intelligent Transportation Systems, 2011, 12(4):1495-1510. [4] Civilis A, Jensen C S, Pakalnis S. Techniques for efficient road-network-based tracking of moving objects[J]. IEEE Transactions on Knowledge & Data Engineering, 2005, 17(5):698-712. [5] Chen Y K, Jiang K, Zheng Y, et al. Trajectory simplification method for location-based social networking services[C]// International Workshop on Location Based Social Networks, Lbsn 2009, November 3, 2009, Seattle, Washington, Usa, Proceedings. DBLP, 2009:33-40. [6] Alt H, Efrat A, Rote G, et al. Matching planar maps[J]. Journal of Algorithms, 2003, 49(2):262-283. [7] Brakatsoulas S, Pfoser D, Salas R, et al. On map-matching vehicle tracking data[C]// International Conference on Very Large Data Bases. VLDB Endowment, 2005:853-864. [8] Zheng Yu. Trajectory Data Mining: An Overview[J]. Acm Transactions on Intelligent Systems & Technology, 2015, 6(3):1-41. [9] Dean J, Ghemawat S. MapReduce: simplified data processing on large clusters[J]. Communications of the ACM, 2008, 51(1): 107-113. [10] Huang J, Qiao S, Yu H, et al. Parallel map matching on massive vehicle gps data using mapreduce[C]// High Performance Computing and Communications & 2013 IEEE International Conference on Embedded and Ubiquitous Computing (HPCC_EUC), 2013 IEEE 10th International Conference on. IEEE, 2013: 1498-1503. [11] Baum L E, Petrie T. Statistical Inference for Probabilistic Functions of Finite State Markov Chains[J]. Annals of Mathematical Statistics, 1966, 37(6):1554-1563. [12] Newson P, Krumm J. Hidden Markov map matching through noise and sparseness[C]// Proceedings of the 17th ACM SIGSPATIAL international conference on advances in geographic information systems. ACM, 2009: 336-343. [13] Koller H, Widhalm P, Dragaschnig M, et al. Fast hidden Markov model map-matching for sparse and noisy trajectories[C]// Intelligent Transportation Systems (ITSC), 2015 IEEE 18th International Conference on. IEEE, 2015: 2557-2561.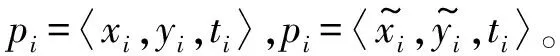
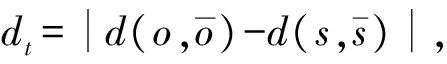
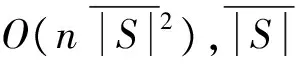
2 基本构想
2.1 分段匹配
2.2 地图冗余
2.3 随机地图分组

2.4 轨迹插点
3 系统架构
3.1 系统框架

3.2 工作流程
4 地图预处理
4.1 地图分区
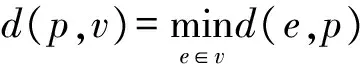

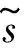
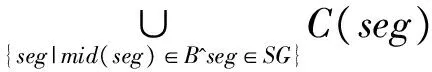
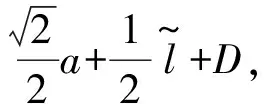
4.2 地图分组
5 基于MapReduce的隐马尔可夫模型
5.1 轨迹碎片化和分布式匹配
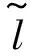
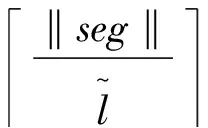
5.2 最优求解
6 实 验
6.1 实验环境
6.2 实验数据
6.3 地图预处理

6.4 计算效率

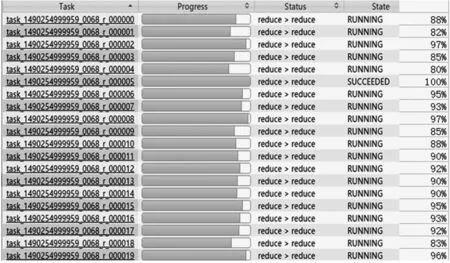
6.5 分布式特性