基于运动扩散模型的含零值降水序列频率计算
李丹丹,宋松柏,李运平
(西北农林科技大学 水利与建筑工程学院,陕西 杨凌 712100)
1 研究背景
水文频率计算是根据水文现象的统计特性,利用现有水文资料,分析水文变量设计值与出现频率(或重现期)之间的定量关系的工作过程,对于水利工程规划、设计、管理以及水资源配置等具有至关重要的作用[1]。降水设计值是进行用水管理的主要依据[2]。通常情况下,水文频率计算采用的水文序列不含有零值,但在干旱和半干旱地区的水文频率分析中,经常遇到包含若干个零值的水文序列,而零是变异范围的下限[3-6]。这些水文序列可能是干旱地区的月降水量,水库设计中的防洪库容系列以及河道断流等[7]。因此,常规的水文频率计算方法无法进行这类水文序列频率计算[8],而且以往研究中对于这类水文序列的频率分析关注较少[9]。Jennings等[4]、Woo等[9]、Wang 等[5]提出了增加小水文值、忽略零值、全概率法以及应用次序统计量构造全序列分布等方法计算含零值水文序列的频率。1980年代以来,我国一些学者也进行了含零值水文序列的计算方法研究,如间接法、中值适线法和Ⅱ型乘法分布等方法[7,11-14]。《水利水电工程设计洪水计算手册》推荐使用频率比例法和Ⅱ型乘法分布法[11,15-17]。张良等[18]利用这两种方法对安固里河洪峰流量进行了分析。2003年,Strupczewski等[8]提出了基于运动扩散模型(Kinematic Diffusion Model,简称KD模型)的含零值序列频率计算模型,这是一种新型的含零值水文序列频率计算方法,该模型已成功地应用于美国干旱地区洪水频率计算,取得了较好的拟合效果。
目前,Strupczewski等推导了KD模型矩法、极大似然法参数计算公式。众所周知,概率权重矩法是水文频率分布参数计算精度较高的方法[19-21]。但是,KD模型目前没有概率权重矩法参数计算公式,且这类模型尚未用于我国含零值水文序列频率计算。本文从概率权重矩定义出发,应用数学变换原理和数值计算原理,严格地推导了概率权重矩法推求KD模型参数计算公式,给出了相应的数值计算方法,并与矩法、极大似然法估计KD模型参数进行比较,为KD模型参数估计方法选择提供依据。以陕西省6个测站2月份降水数据为例,验证概率权重矩法计算KD模型参数公式正确性,并与频率比例法和II型乘法分布法进行对比,研究KD模型在我国含零值降水序列频率计算的普适性,以期为我国含零值水文序列频率计算提供一种新的计算方法。
2 含零值水文序列概率模型及运动扩散模型
2.1含零值水文序列概率模型基于概率论观点,含零值水文序列中零值出现的概率不等于零,在概率密度函数图中具有不连续性,因此,这类水文序列的概率密度函数可表示为[8]:

式中:β为零值事件发生的概率,即可按泊松过程进行估计;为连续函数,且满足R为矢量参数;δ(x)为Dirac delta函数,即
2.2运动扩散模型根据完全线型圣维南方程可推得表示运动波的运动扩散模型(KD模型),其脉冲响应函数可表示为[8]:

式中:Pi(λ)服从泊松分布;服从Gamma分布;参数α,λ为关于河道形态和水流条件的函数;1(t)为单位阶跃函数,
Strupczewski等[22]指出,对于有限河段而言,基于物理参数的马斯京根模型等价于KD模型,式(2)可以表示为概念元素的网络级联,即线性水库和水文中常用的线性河道。Einstein[23]指出式(2)所给函数可作为推移质输沙的确定性随机模型。Eagleson[24]提出,在假设暴雨发生次数遵循泊松分布、暴雨深度服从指数分布的条件下,式(2)可以作为总降水量频率计算的分布函数。因此,Strupczewski等[22]认为式(2)可以用于含零值水文序列频率计算。
3 运动扩散模型概率密度函数推导
将KD模型脉冲响应函数变量t替换为变量x,得到双参数概率分布函数[8]:

式中:z为泊松分布随机变量;x为Gamma分布随机变量。
式(3)等号右侧第一项可表示为:

根据第一类一阶修正Bessel函数及x>0时1(x)=1,第二项可表示为:
将式(4)—(5)代入等式(3)得:
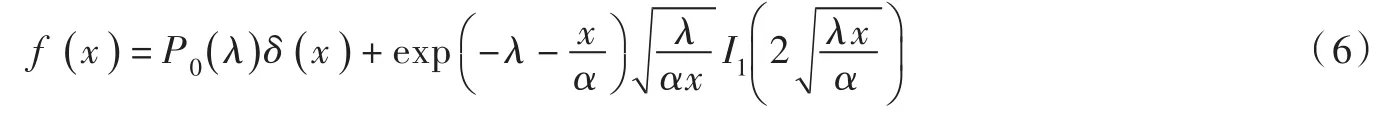
式(6)即为KD模型的概率密度函数,简称KD-PDF。因此,只要参数α、λ已知,就可以通过KD模型求得零值概率和非零值事件发生概率。
4 运动扩散模型参数估计及设计值推求
4.1参数估计
(1)矩法参数估计根据累计量与矩的关系,可得[8]:

式中:μ′1为一阶原点矩;μ2为二阶原点矩;Cv为变差系数;μ′1、μ2和Cv可用样本估算值代替。
(2)极大似然法参数估计根据Strupczewski等[8]的推导,KD模型分布参数与极大似然估计值的关系为:

式中:n为序列总长度;为n阶贝塞尔函数;xj为第j个样本值。
显然,式(10)为λ的函数,求解该非线性方程,即可获得参数,代入式(9)可获得参数。其初值确定可以通过零值概率推求。
(3)概率权重矩法参数估计根据概率权重矩的定义,KD模型的零阶概率权重矩为:

KD模型一阶概率权重矩为:
式中:
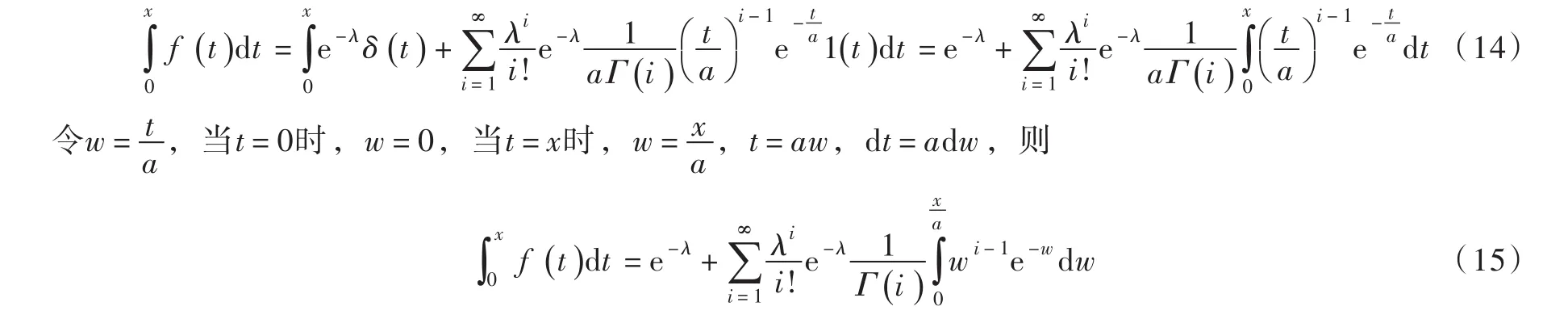
将式(6)和式(15)代入式(13)中有:

则M1=w1+w2,经化简可得:

令g=2s,当s=0时,g=0,当s=∞时,则

因此,KD模型概率权重矩为:
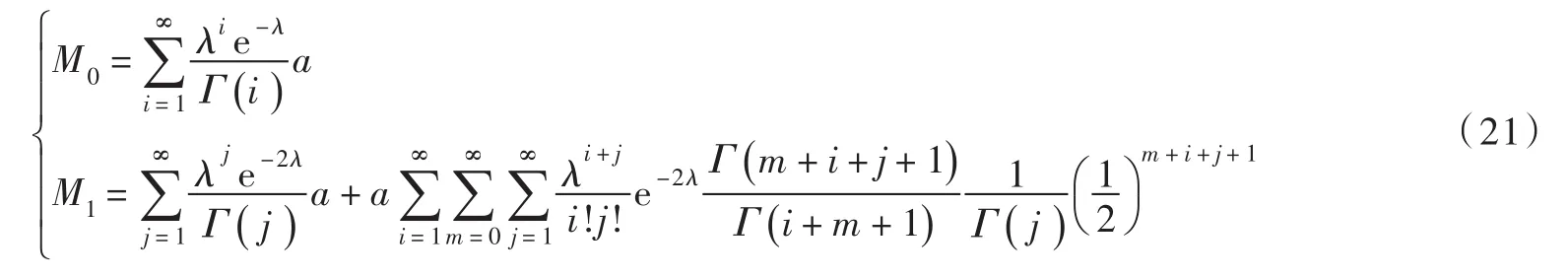
概率权重矩法与传统矩法一样,用样本概率权重矩作为总体概率权重矩的估计量,而样本概率权重矩与分布无关。因此KD模型参数与概率权重矩关系为:

式中:l为将样本按由小到大顺序排列的序号;为相应于序号l的样本值;其余参数意义同前。
4.2设计值推求对于给定的xp,其超越概率根据式(23)计算。

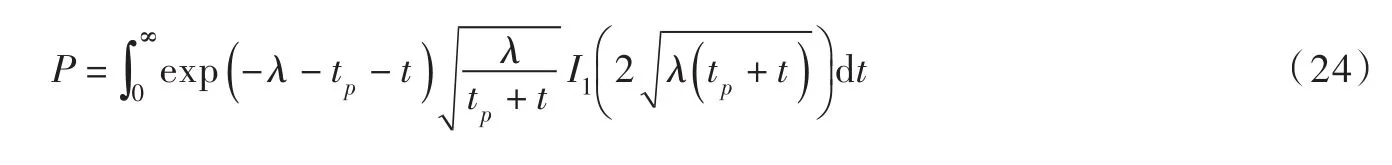
5 频率比例法与Ⅱ型乘法分布法
5.1频率比例法频率比例法在进行频率分析时,只分析非零的部分序列,然后通过频率转化得到全序列的频率曲线,又称间接法[14]。
首先,将n2项非零资料视作一个独立系列,按P-Ⅲ型分布(Cs=2Cv)进行频率分析计算,各点的经验频率为然后通过参数计算、调整和适线等常规方法,求得一条频率曲线。但此线只能代表全部n项资料中一部分资料的分布情况,而任意一个样本值xi的频率,可以通过下列转换求得:

式中:Pb相应于全部系列的频率;Pa相应于n2项系列的频率。点绘各xi点的Pb,可以连成一条新的频率曲线,即为所求的频率曲线。
5.2Ⅱ型乘法分布法Ⅱ型乘法分布法是从独立随机变量的概率乘法定理引伸出来的。对于标准化变量模比系数及均值频率b=P(K≥1),严格服从概率乘法定理的原始乘法分布即[14]:

考虑到充分利用均值频率b的有益信息,以b值为分界把(0,1)频率区间分为首尾两部分,建立起Ⅱ型乘法分布,其概率密度函数为:

式中:a、c分别为首、尾部密度函数参数,b的变幅一般在0.2~0.8之间。
Ⅱ型乘法分布法中均值频率b可以从样本系列求出均值后,在经验频率曲线上查读或内插b=P(K≥1)。对于确定的b值,密度参数a和c可直接由式(28)估计。

在(0,1]区间内的每一个尾部变量均可单独提供参数c的信息,当k=0时,用k=0.00001代替。在[1,∞)区间内的每一个首部变量,均可以单独提供参数a的信息。
6 模型应用
以陕西省宝鸡、泾阳、咸阳、乾县、武功、兴平6个测站2月份降水序列为研究对象,在矩法、极大似然法估计KD模型参数的基础上,验证概率权重矩法在KD模型参数估计中的应用效果,并与频率比例法、Ⅱ型乘法分布模型进行对比,采用AIC准则、OLS准则和残差平方和(RSS)最小准则进行拟合优度评价,研究KD模型的适用性。经审查,资料满足一致性要求,资料序列长度如表1所示。

表1 陕西省6测站2月份降水资料系列
6.1参数估计利用矩法和极大似然法以及概率权重矩法对KD模型参数α和λ进行计算;在计算样本均值、标准偏差以及变差系数基础上,根据非零序列推求P-Ⅲ型分布参数α、β、γ;根据式(28)计算Ⅱ型乘法分布模型参数a、b、c。研究区6个测站分布参数见表2。

表2 陕西省6测站降水量分布3种计算方法参数估计结果
由表2可知,KD模型的3种参数估计方法所估计的参数值存在一定差异,但又有一定规律。3种参数估计方法中,极大似然法估计得到的α值最大,λ值最小,矩法估计得到的λ值最大,α值最小,概率权重矩法得到的得参数值介于二者之间。基于P-Ⅲ分布的频率比例法在参数计算过程中,位置参数γ为负值。Phien等[25]提出,利用P-Ⅲ分布进行降水量频率计算时,若获得γ为负值时,通常将γ设置为零,转换为两参数Gamma分布计算。经计算,基于Gamma分布的频率比例法参数见表3。

表3 基于Gamma分布的频率比例法参数
6.2频率曲线绘制根据参数估计结果,利用KD模型、频率比例法以及Ⅱ型乘法分布法模型对6个测站含零值降水序列进行频率计算,并绘制频率曲线,如图1所示。
由图1可以看出,KD模型对于含零值降水序列的拟合效果优于频率比例法与Ⅱ型乘法分布法。KD模型与Ⅱ型乘法分布法对于尾部拟合效果优于频率比例法,其主要原因是KD模型与Ⅱ型乘法分布法在频率计算过程中将含零值水文序列作为一个整体,近似为连续分布进行计算,而频率比例法是将含零值水文序列分为零序列和非零序列两部分,通过非零序列计算含零值水文序列。
6.3拟合优度评价采用OLS准则、AIC准则和RSS最小准则对KD模型、频率比例法、Ⅱ型乘法分布法频率曲线进行拟合优度评价,计算结果见表4。
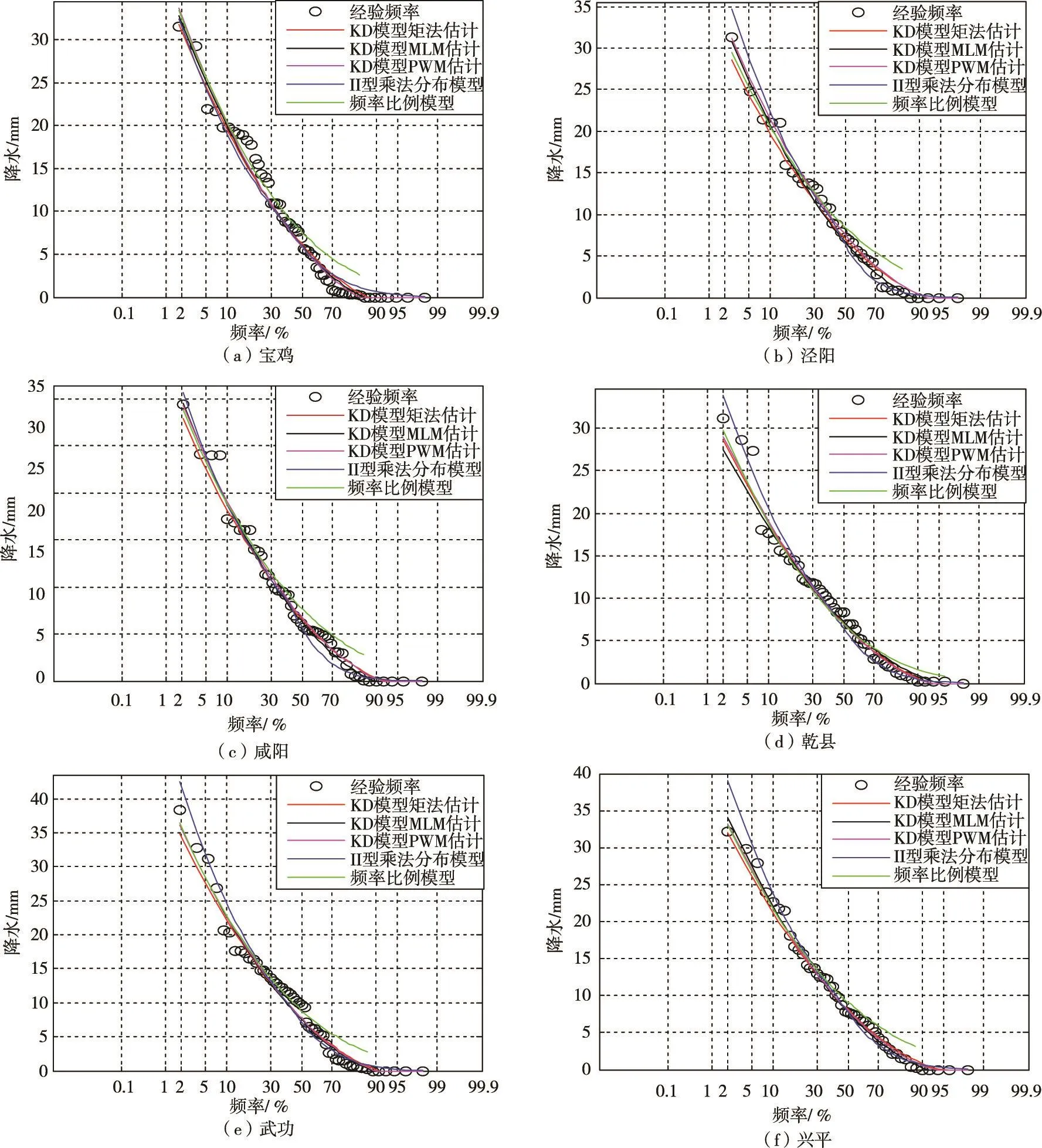
图1 陕西省6测站2月降水量频率曲线
由表4可以看出,基于OLS准则、AIC准则和RSS最小准则的曲线拟合优度评价结果基本一致,且与频率曲线图所反映的结果相同,其中RSS结果明显反映出KD模型拟合效果优于频率比例法和Ⅱ型乘法分布法。分析KD模型3种参数估计方法拟合优度结果可知,矩法估计拟合效果最差,极大似然法估计拟合效果与概率权重矩法估计拟合效果相近,但概率权重矩法估计拟合效果略优于极大似然法估计拟合效果。
7 结论
本文应用概率权重矩法定义,严格地推导了KD模型含零值序列频率计算参数估计公式。以陕西省6个测站2月份降水资料为例,选取3种频率计算模型进行含零值降水序列频率分析,并进行拟合优度评价,探讨KD模型的适用性,优选适用于KD模型的参数估计方法,以期为含零值降水序列频率计算提供理论依据。
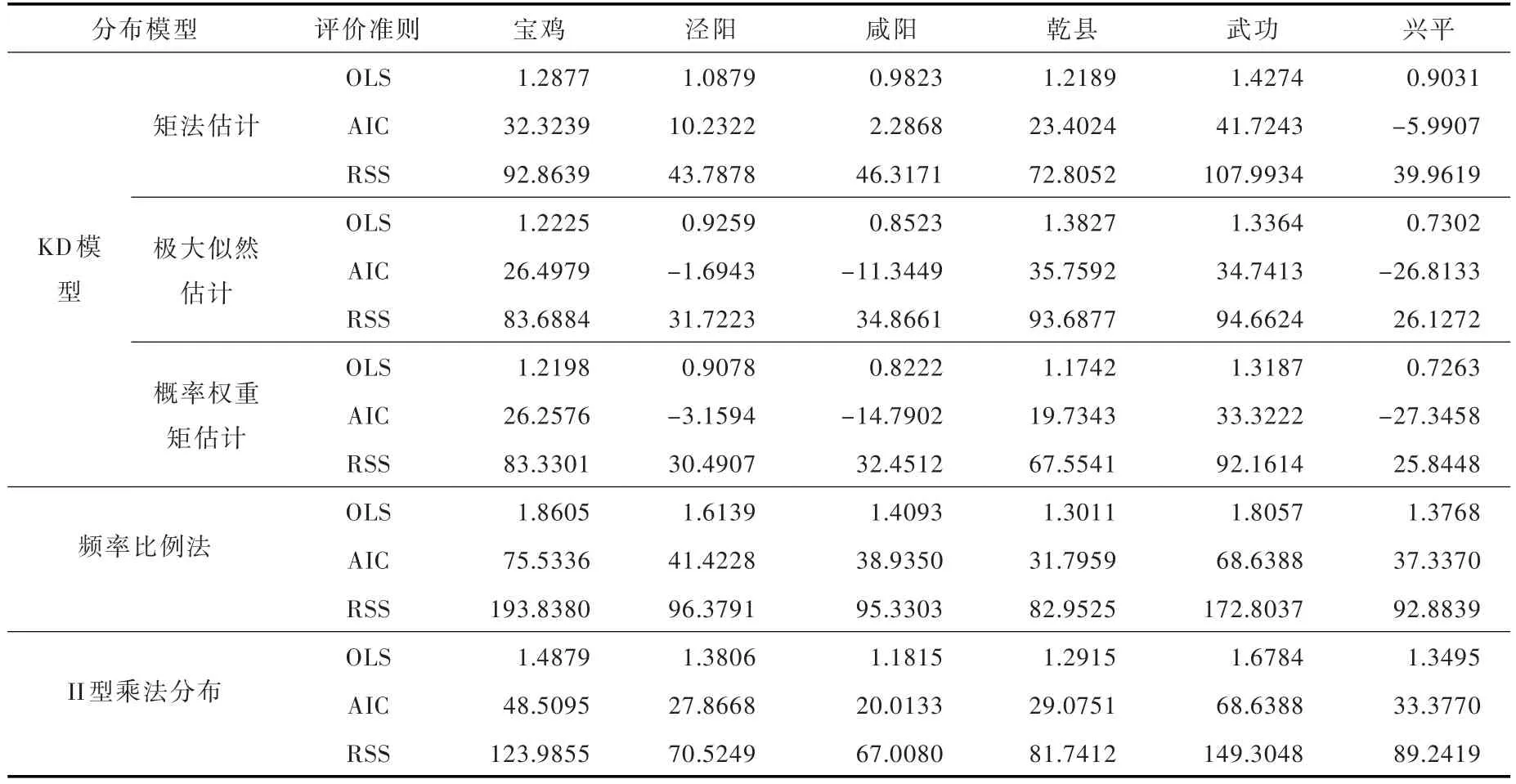
表4 陕西省6测站2月份降水量的拟合优度评价结果
(1)选用KD模型模型、频率比例法、Ⅱ型乘法分布法对含零值降水序列进行频率计算,探讨KD模型适用性,结果表明,KD模型可以用于含零值降水序列频率计算,且拟合效果优于频率比例法及Ⅱ型乘法分布法。该方法具有一定的物理基础,虽然包含一些复杂的数值计算,但是,借助于计算机编程,不难实现含零值降水序列的频率计算。
(2)对比分析矩法、极大似然法、概率权重矩法估计KD模型参数,结果表明,概率权重矩法优于矩法和极大似然法,文中推导的概率权重矩法计算KD模型参数公式是正确的。
(3)根据OLS准则、AIC准则和RSS最小准则评价曲线拟合优度,结果显示,采用概率权重矩法参数估计的KD模型对含零值降水序列频率曲线拟合度最优。文中模型以期为含零值水文频率计算提供一种新的计算方法。
参考文献:
[1]黄振平,陈元芳.水文统计学[M].北京:中国水利水电出版社,2011.
[2]马晓晓,宋松柏.基于Copula函数的不完全降水序列频率计算方法研究[J].水力发电学报,2017,36(2):9-17.
[3 ]ZHANG L,SINGH V P.Frequency analysis of flood damage[J].Journal of Hydrologic Engineering,2005,10(2):100-109.
[4]JENNINGS M E,BENSON M A.Frequency curves for annual flood series with some zero events or incomplete data[J].Water Resources Research,1969,5(1):276-280.
[5]WANG S X,SINGH V P.Frequency estimation for hydrological samples with zero values[J].Journal of Water Resources Planning and Management,1995,121(1):98-108.
[6]WEGLARCZYK S,STRUPCZEWSKI W G,SINGH V P.Three-parameter discontinuous distributions for hydrological samples with zero values[J].Hydrological Processes,2005,19(15):2899-2914.
[7]宋松柏,康艳.含零值水文序列频率的计算原理与应用[J].水文,2012,32(5):22-26.
[8]STRUPCZEWSKI W G,WEGLARCZYK S,SINGH V P.Impulse response of the kinematic diffusion model as a probability distribution of hydrologic samples with zero values[J].Journal of Hydrology,2003,270(3/4):328-351.
[9 ]WOO MingKo,WU Kai.Fitting annual floods with zero-flows[J].Canadian Water Resources Journal,2013,14(2):10-16.
[10]杨力行.Ⅱ型乘法分布在干旱资料含零系列统计分析中的应用[J].水文,1992(3):21-24.
[11]李满刚.具有零项系列的中值适线法[J].山西水利科技,1998(1):27-29.
[12]毛赛珠.具有零项系列的中值适线法[J].水文,1985(6):29-31.
[13]刘志强,王成雄,白霜 .频率比例法在干旱地区含零系列分析中的应用[J].东北水利水电,1999(1):31-35.
[14]水利部长江水利委员会水文局,水利部南京水文水资源研究所.水利水电工程设计洪水计算手册[M].北京:中国水利水电出版社,1995.
[15]杨力行,陈容.Ⅱ型乘法频率曲线[J].新疆农业大学学报,1987(1):48-58.
[16]刘大秀.Ⅱ型乘法频率曲线的统计参数及特征[J].新疆农业大学学报,1987(1):58-66.
[17]杨力行,陈容,刘大秀.Ⅱ型乘法频率曲线应用可行性研究[J].新疆农业大学学报,1988(1):57-64.
[18]张良,刘鑫杨.含零序列水文频率计算方法在张北水文站的应用探讨[J].海河水利,2017(1):36-38.
[19]宋德敦,丁晶.概率权重矩法及其在P-Ⅲ分布中的应用[J].水利学报,1988(3):1-11.
[20]宋德敦.不连序系列统计参数计算的新方法——概率权重矩法[J].水利学报,1989(9):25-32.
[21]秦大庸,孙济良.概率权重矩法在指数γ分布中的应用[J].水利学报,1989(11):1-9.
[22]STRUPCZEWSKI W G,NAPIORKOWSKI J J,DOOGE J C Z.The distributed Muskingum model[J].Journal of Hydrology,1989,111(1/4):235-257.
[23]EINSTEIN H A.Formulas for the transportation of bed load[J].Transactions of the American Society of Civil Engineers,1947,107(1):561-597.
[24]EAGLESON P S.Climate,soil,and vegetation:2.The distribution of annual precipitation derived from observed storm sequences[J].Water Resources Research,1978,14(5):713-721.
[25]PHIEN H N,NGUYEN V T V.Derivation of the Pearson type(PT)III distribution by using the principle of maximum entropy(POME)[J].Journal of Hydrology,1987,90(3/4):351-355.

