无刷双馈感应电机统一矢量模型的研究

刘　石，段琦玮，龙　腾

(1.华北电力大学能源动力与机械工程学院，北京 102206；2.剑桥大学工程系，剑桥 CB21TN)

0　引言

无刷双馈电机(brushless doubly-fed machines,BDFM)是一种新型电机。其既可以作为调速用电动机，也可以作为发电机代替双馈感应电机(doubly-fed induction machines,DFIM)[1]。BDFM的定子由两套独立、无直接耦合的三相绕组组成。功率绕组(power windings，PW)直接与电网连接，控制绕组(control windings，CW)接变频电源。转子主要有两种结构：特殊笼型转子[2-3]和磁阻转子[4]。本文研究所用样机为一台无刷双馈感应电机(brushless doubly-fed induction machines,BDFIM)，其PW和CW的极对数比为4∶1，转子每个笼型结构有五个回路，没有公共端环。

目前针对BDFM的研究热点主要为电机建模、本体分析及优化三个方向。俄亥俄州立大学的研究团队在1989年首次提出了BDFIM在三相静止坐标系下的多回路数学模型，并对其进行了仿真验证[5-7]；依据此模型，该团队又提出了BDFIM转子速两相坐标系下的模型[8]。基于转子速两相坐标系下的模型，陆续有研究人员提出各种改进模型及其控制策略[9-11]。2002年，西班牙学者J.Poza提出了考虑笼型转子特殊结构的统一坐标系下的矢量模型。此模型将转子每个笼型结构中的回路数等效为一个，并基于此给出了矢量控制策略[12]。2005年，剑桥大学的Roberts详细阐述了一个统一的动态和静态模型——耦合电路模型，并给出了在耦合电路模型和d-q坐标系下的电机参数计算方法。但由于耦合电路模型过于复杂，其无法用于控制方法的分析和研究[13]。2008年，Farhad等人提出了BDFIM的统一矢量模型，并在转子磁链矢量定向坐标系下对模型进行了仿真验证。该模型考虑了转子每一笼型中所有环路的影响，同时可以通过对自由变量的不同取值将模型定位于不同的坐标系[14]。2015年，Sajjad 提出了基于两定子电流和磁链矢量的转矩方程。但该方程经过了简化，因此无法保证对模型预测的精确度[15-16]。

本文对BDFIM的统一矢量模型进行了分析，得出了PW电流矢量、CW电流和磁链矢量、转子电流和磁链矢量关于PW磁链矢量的表达式。将各个表达式代入电机的电磁转矩方程和功率方程中，得出了更为简洁明了的表达式，从而更方便地得出电磁转矩和功率同电机物理量之间的关系，为控制方法的研究带来了便利。同时，可以通过对自由变量取不同的值，得到定位于不同坐标系下的电磁转矩和功率方程。为了验证理论公式的准确性，搭建了变频调速平台进行试验研究。为了简化试验流程，选取α-β静止坐标系模型。通过实际测量值和理论计算值波形的对比，验证了理论方程的准确性。

1　BDFIM的统一矢量模型分析

1.1　统一矢量模型方程

无刷双馈感应电机同步运行时(双馈模式)的转子角速度为：

(1)

式中：ω1、ω2分别为功率绕组、控制绕组产生的旋转磁动势的电角速度；p1、p2分别为功率绕组、控制绕组的极对数；“±”中的“+”、“-”分别为电机运行于超同步、亚同步模式。

统一矢量模型的电压、磁链和转矩方程分别为：

(2)

(3)

(4)

式中：η和γ由式(5)给出。

(5)

1.2　统一矢量模型分析

(6)

由式(6)可得式(7)。

(7)

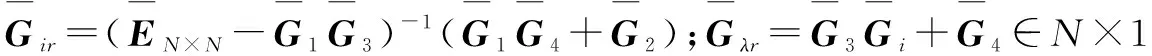
将式(7)代入式(3)和式(6)，得式(8)。

(8)

2　转矩和功率表达式

本节根据上文所推导出的关系式，对电机的转矩和功率方程进行推导变换。

2.1　转矩表达式

将式(3)和式(8)代入转矩方程式(4)，相比得转矩方程式(9)。

(9)

与式(4)相比，式(9)所示的转矩方程消除了转子电流矢量，使得方程中的变量都为可控量，更有利于对转矩的解耦控制进行研究。

2.2 功率表达式

无刷双馈电机的功率方程为：

(10)

将式(2)中的PW电压方程和式(8)中的PW电流方程代入功率方程式(10)，可得有功功率和无功功率的新表达式(11)。

(11)

与式(10)相比，式(11)所示的功率方程消除了PW电压矢量，使得方程中的变量都为可控量；同时，表明了PW电流矢量幅值和PW磁链矢量微分对电机功率起到的作用，因此更有利于对功率的解耦控制进行研究。

2.3　α-β静止坐标系下的转矩和功率方程

(12)

(13)

(14)

3　试验验证

3.1　试验平台搭建

为了验证转矩和功率方程的正确性，针对试验样机，搭建了变频调速试验平台。BDFIM样机与直流电机通过联轴器连接，联轴器上安装有三晶JN338-A转矩转速测量仪，用于测量样机的转速和转矩值；BDFIM的PW直接与220 V、50 Hz的电网连接，CW由变频器供电；直流电机由一个直流稳压源供电。样机上装有三个空气开关，可以切换不同的运行模式。电机空载启动时，将CW短接，使CW接入直流电压迁入同步运行；CW变频器供电时，电机就可以运行于超同步或亚同步状态。运行中，电机有功和无功功率值由功率测量仪测定。

3.2　试验验证

本节通过对比电机不同运行状态下转矩和功率的测量值和计算值，验证了理论表达式的准确性。

图1为电机空载时转速梯形变化的转速、转矩、有功功率和无功功率的波形。电机短接启动后，CW接直流电压迁入同步速600 r/min。稳定后：在2 s时，CW改由变频器供电进入超同步运行660 r/min；在3 s时，变频器供电电压相位反向电机亚同步运行540 r/min；在4 s时，电机又回到超同步运行状态660 r/min，电机一直保持为空载状态。

图1　转速、转矩和功率波形(转速梯形变化)Fig.1　Waveforms of speed,torque and power(speed trapezium change)

图2为电机超同步运行(660 r/min)、负载转矩变化时的转速、转矩、有功功率和无功功率的波形。电机空载短接启动后，CW接直流电压迁入同步速600 r/min。稳定后：在2 s时，CW改由变频器供电进入超同步运行660 r/min；在3 s时，电机由空载加负载到50 N·m；在4 s时，电机由50 N·m加负载到100 N·m。

由图1和图2的试验波形可知，电机在定转矩变转速和定转速变转矩两种基本运行状态下，转矩方程和功率方程都能比较精确地跟随电机实际转矩值和功率值，表明了式(13)和式(14)的正确性。由此证明了统一矢量模型理论推导的转矩方程(9)和功率方程(11)可以作为BDFIM的理论模型，以进行控制策略的研究。

此外，图1和图2中由式(13)和式(14)计算出的转矩值和有功功率值大于实测转矩值和功率值。其原因是统一矢量模型没有考虑铁芯饱和，同时又忽略了试验中存在的摩擦。

图2　转速、转矩和功率波形(负载转矩变化)Fig.2　Waveforms of speed,torque and power(load torque change)

4　结束语

参考文献:

[1] MCMAHON R A,ROBERTS P C,WANG X.Performance of BDFM as generator and motor[J].Electric Power Applications,IEEE Proceedings,2006,153(2):289-299.

[2] 李冰,刘石.无刷双馈电机模糊直接转矩控制系统研究[J].自动化仪表,2016,37(12):10-13.

[3] 段琦玮,刘石,龙腾.统一矢量模型的无刷双馈电机的转速控制[J].自动化仪表,2017,38(6):1-5.

[4] HSIEH M F,CHANG Y H,DORRELL D G.Design and analysis of brushless doubly fed reluctance machine for renewable energy applications[J].IEEE Transactions on Magnetics,2016,52(7):1-5.[5] WALLACE A K,SPEE R,LAUW H K.Dynamic modeling of brushless doubly-fed machines[C]//Industry Applications Society Meeting,2002:329-334.

[6] SPEE R,WALLACE A K,LAUW H K.Performance simulation of brushless doubly-fed adjustable speed drives[C]//Industry Applications Society Meeting,1989:738-743.

[7] LI R,WALLACE A,SPEE R.Dynamic simulation of brushless doubly-fed machines[J].IEEE Transactions on Energy Conversion,1991,6(3):445-452.

[8] LI R,WALLACE A,SPEE R.Two-axis model development of cage-rotor brushless doubly-fed machines[J].IEEE Transactions on Energy Conversion,1991,6(3):453-460.

[9] ZHOU D，SPEE R，ALEXANDER G C.A simplified method for dynamic control of brushless doubly-fed machines[C]//Conference of the IEEE Industrial Electronics Society,1996:946-951.

[10]ZHOU D,SPEE R,ALEXANDER G C.Experimental evaluation of a rotor flux oriented control algorithm for brushless doubly-fed machines[J].IEEE Transactions on Power Electronics,1997,12(1):913-919.

[11]HUANG S.Study of the control strategy on rotor field orientation for brushless doubly-fed machine[J].Transactions of China Electrotechnical Society,2002,1(2):508-513.[12]POZA J,OYARBIDE E,ROYE D.Unified reference frame dq model of the brushless doubly fed machine[J].Electric Power Applications Iee Proceedings,2006,153(5):726-734.

[13]ROBERTS I,CHRISTOPHER P.A study of brushless doubly-fed(induction) machines:contributions in machine analysis,design and control[J].Genetics,2005,148(3):1353-1365.[14]BARATI F,ORAEE H,ABDI E.Derivation of a vector model for a brushless doubly-fed machine with multiple loops per nest[C]//2008 IEEE International Symposium on Industrial Electronics,2008.[15]BARATI F,ORAEE H,ABDI E.The brushless doubly-fed machine vector model in the rotor flux oriented reference frame[C]//Conference of the IEEE Industrial Electronics Society,2008.

[16]BARATI F,SHAO S,ABDI E.Generalized vector model for the brushless doubly-fed machine with a nested-loop rotor[J].IEEE Transactions on Industrial Electronics,2011,58(6):2313-2321.