浙教版初中数学几何例习题有效改编的探究

曹益军

（浙江省杭州市萧山区靖江初中，浙江杭州　311223）

1　研究背景

2014年，萧山教育局出台《萧山区中小学教师教学规范（修订稿）》，其中对教师“教学准备”有如下要求：第2条深度研究教学材料。充分研读教材，形成自己独特的理解，同时学习参考其他教学资料，正确理解教学内容，把握教学重点和难点。对用于教学的各种练习，要采用“教师自己先做”的方式进行研究，感悟解题的规律和思路，揣摩学生在解题过程中可能遇到的困难和障碍。

第6条精心准备各类作业。根据教学目标与学生实际精心选用和编创作业。作业难度合理，数量适当。关注学生的个体差异，增强作业的层次性和可选择性，满足不同学生的需求。根据学科特点丰富作业的形式，增加观察积累、动手操作、搜集整理、发现探究、劳动服务等作业形式。积极探索以引领学生全程学习为目的的导学新作业模式。

现实教学过程中，教师很多是拿来主义，对已有的教材例题、习题改编的意识不强，在备课中不能对例题、习题进行深层次的挖掘、拓展、再创造，在授课时也往往出现一笔带过、草草了事的教学现状，根本没有很好的利用例题、习题的所潜在的价值，而教材例题、习题的“二次开发”能促使学生的学习方式由“重结论轻过程”向“过程与结果”并重的方向发展，使学生挖掘隐含问题的本质属性，从而达到“做一题，通一类，会一片”的解题境界，摆脱题海，实现“轻负高效”。

笔者的研究，是结合本学校的自主教学的实际情况，探讨如何更有效地对例题与习题进行合理的选择、独特的设计、有效的教学，力求进一步提高我校自编导学案的质量，并以此为契机，提高本学科教学质量，提升学校办学品质。

2　实践探微

2.1　改编策略实施

数学问题改编是对已有数学问题的条件和结论部分的内容、结构、情境等进行改造，得出新题的一种命题设计方法。改编题较之原本习题不仅承载了知识内容，蕴含了数学思想方法，还被赋予了新的问题情境，传导了改编者的设计意图，并以此通过巩固和变式训练来实现教学目标。

改编问题的具体方法有：转换条件与结论、否定条件、题组整合等。

2.1.1　转换条件与结论

转换条件与结论，即把原题中的结论与部分条件互换，使之产生新的问题。如下例：

原题呈现：教科书九上4.5节《相似三角形的性质及其应用》习题 A3（P142）。

已知：如图1，在△ABC中，AD是角平分线，∠ADE=∠B。

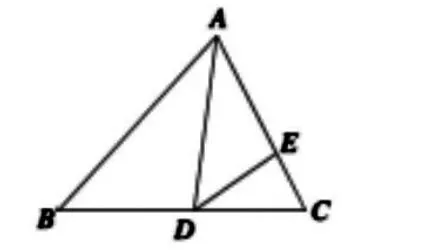
图1　

求证：AD2=AE·AB

其中， 条件有：（1）AD 是角平分线，（2）∠ADE=∠B，结论有：AD2=AE·AB。

转换其中的条件和结论，可得：

改编一，已知：如图1，在△ABC中，AD是角平分线，AD2=AE·AB。

求证：∠ADE=∠B。

改编二，已知：如图 1，在△ABC 中，AD2=AE·AB，∠ADE=∠B。

判断AD是否为△ABC的角平分线，并说明理由。

改编一，是对三角形相似判定的复习，改编二，是不能判定它为角平分线的，这也是学生在相似判定中的一个易错点。

转换条件与结论的方法，适合大多数例题和习题，也是最常用的改编方法。

2.1.2　否定条件法

否定条件法的策略实施，大致可分为四个步骤：

步骤1，选择习题。

步骤2，列出各个条件。

步骤3，否定各个条件，列出相应的新条件。

步骤4，根据新条件，提出新问题。

下面结合一道平行四边形（三角形的中位线）中的课后作业题，具体说明否定条件策略在习题改编中的应用。

原题呈现：如图2，C、D是线段AB上两点，且AC=BD=AB=1，点P是线段CD上一个动点，在AB同侧分别作等边△PAE和等边△PBF，M为线段EF的中点,在点P从点C移动到点D时，点M运动的路径长度为多少？

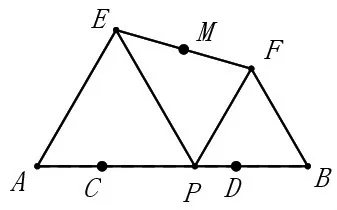
图2　

第一步，我们首先在步骤1上列出问题中的各个条件：

条件1：C、D是线段AB上两点；

条件3：在AB同侧；

条件4：等边△PAE和等边△PBF；

条件5：M为线段EF的中点；

条件6：点P从点C移动到点D；

条件7：点M运动的路径长度。

第二步，在步骤2上，我们可依次对所列条件进行否定，并列出新的条件：

条件1否定：“C、D不是线段AB上两点”，如：点C在线段AB延长线上，情况将如何？

条件 2 否定：“AC≠BD”或“AC=BD≠1”，如:AB=m，AC+BD=n等。

条件3否定：“在AB异侧”，则情况将如何？

条件4否定：“△PAE和△PBF不是等边三角形”，如:两个三角形都为等腰三角形，或为正方形，或为其他特殊多边形。

条件5否定：“M不是EF的中点”，如:M是EF的三等分点。

条件6否定：“点P不是线段CD上一个动点”，如:点P在线段AB上运动。

条件7否定：“不求点M运动的路径长度”，如:求PM的长度范围，等等。

第三步，在步骤3上，我们利用一个或若干个新条件提出新问题。

改编一，利用新条件2和4，我们可以得到如下新的问题：

如图3，线段AB=m，C、D是AB上两点，且AC+BD=n，点P是线段CD上一个动点，在AB同侧分别作等腰Rt△PAE和等腰Rt△PBF，M为线段EF的中点。在点P从点C移动到点D时，点M运动的路径长度为多少？

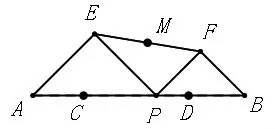
图3　

改编二，利用新条件6和7，我们可以得到如下新的问题：

如图4，已知AB=6，点P是线段AB上一个动点，在AB同侧分别作等边△PAC和等边△PBD，M为线段CD的中点，连接PM。在点P从点A移动到点B的过程中，求线段PM的最小值。

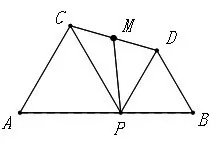
图4　

改编三，利用新条件4和7，我们可以得到如下新的问题：

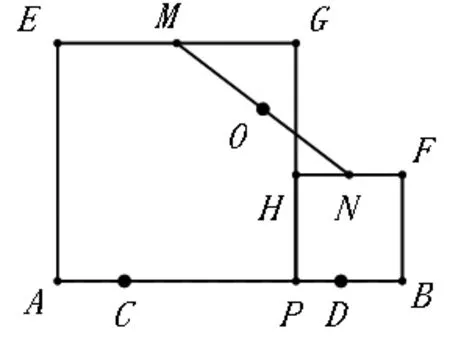
图5　

通过以上案例，我们可以看到，从一个给定的数学问题出发，利用否定条件的策略，以一生十，可以提出丰富多彩的问题。当然，在利用新条件提出问题时，会遇到新条件和其他未被否定的原条件之间不相容的情形，此时提出的问题将是无效的。众所周知，提出问题比解决问题更重要，我们积极利用否定条件策略，研究问题，这将会编拟出更精彩的数学问题。教师积极引导学生利用否定条件策略提出问题，这将更能考查一个学生对知识的理解和掌握情况，必将收到事半功倍的效果。

2.1.3　题组整合

重组整合，顾名思义，借助一定的素材，将彼此联系紧密的一些例题、习题，串联或并联起来，可以构造出一系列的新问题。如下例：

原题呈现：教科书八上2.1节《图形的轴对称》例2（P50），如图6，L表示草原上的一条河。一少年从A地出发，骑着马去河边，让马饮水，然后回位于B地的家中。他沿怎样的路线行走，能使路程最短？做出这条最短路线。

图6　

本题是利用轴对称性质（PA=PA’）和三角形三边关系（或两点间线段最短），解决最值问题。此类问题和解题方法在各种资料中出现颇多，收集并重组整合后，可以得到不少新问题。

改编一，增加一条线（作业本中练习题）：

如图7，点P在锐角∠AOB内，M、N分别为边OA、OB上任意一点，连结PM、PN、MN，当△PMN周长最小时，请在图上确定M、N的位置。若OP=3，∠AOB=30°，则最小周长为多少。

图7　

图8　

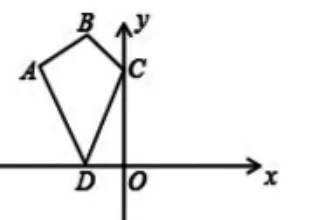
图9　

改编二，增加一个点（导学作业本习题）：

如图8，点P、Q在锐角∠AOB内，M、N分别为边OA、OB 上任意一点，连结 PQ、PM、QN、MN，当四边形PMNQ周长最小时，请在图上确定M、N的位置。

改编三，把锐角变为直角坐标系（中考题）：

如图 9，在直角坐标系中有四个点 A（-3，3），B（-2，5），C、D分别在y轴和x轴上，当四边形ABCD周长最短时，求C、D的坐标。

改编四，与平移变换结合（中考题改编）：

如图10，在直角坐标系中有线段AB=2，CD=1，A（1，2）、B（3,2），C、D 为 x 轴上任意点，当四边形 ABCD周长最短时，求C的位置。

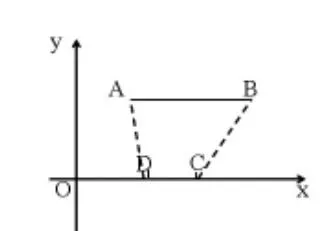
图10　

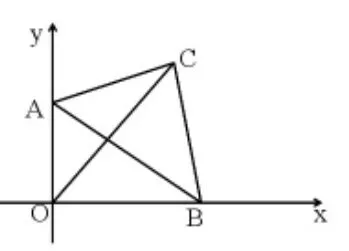
图11　

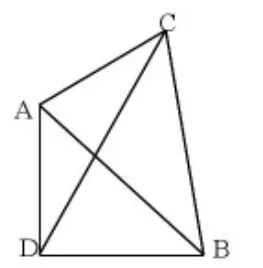
图12　

改编五，与旋转变换结合（中考题改编）：

如图 11，在△ABC 中，AC=3，BC=4，AB=5，顶点 A、B分别y轴和x轴上，当A在y轴上运动时，B随之在x轴上运动。求运动过程中，点C到点O的最大距离。

改编六，与旋转变换结合（中考题改编），提升难度：

在改编四基础上，如图12，△ABC中，AC=a，BC=b，AB不定，即∠ACB任意，以AB为边作等腰直角△ABD。当∠ACB变化，且点D与点C位于直线AB的两侧，求CD的最大值。

此组例题的改编组合，不仅拓展了轴对称性质的应用，而且配以平移、旋转的改编题，让学生意识到学习图形变换的真谛：在改变图形位置、方向后不改变其大小和形状，图形变换是分析问题的一种工具。

通过重组整合，改编习题，在强大的网络资源面前，会非常快捷有效，尤其是在中考复习阶段，被大多数老师所采用，可以快速地形成知识体系。

2.2　经典案例分析

原题呈现：教科书九上4.5节《相似三角形的性质及其应用（3）》作业题 B5（P149），有一块三角形余料 ABC见图13，它的边BC=120mm，高线AD=80mm，要把它加工成正方形零件，使正方形的一边在BC上，其余两个顶点分别在AB，AC上。求加工成的正方形零件的边长。

图13　

本题考查：（1）正方形的性质，（2）直角三角形的性质，（3）相似三角形的判定和性质，（4）方程，（5）基本的几何分析推理能力。潜在价值：渗透了数形结合和建模的思想，应用知识的能力要求较高，能拓展学生的思维空间，提高知识的迁移能力和学生的创新能力。

改编策略一：否定一个条件，如改变其中一个图形的形状。

例1：内部四边形改为矩形，如图14，有一块三角形余料ABC，它的边BC=120mm，高线AD长80mm，四边形PQRS是三角形的内接矩形。

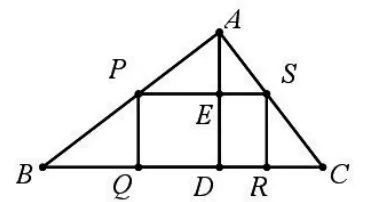
图14　

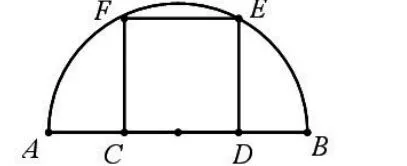
图15　

（1）当矩形PQRS与△ABC的面积之比为3∶8时，求矩形PQRS的周长；

（2）设PQ长为xmm，求矩形面积S关于x的函数表达式，并说明点P在何处时矩形的面积最大？

例2：外部三角形改为半圆，如图15，半圆的直径AB=10，C、D为直径上的点，E、F为半圆弧上的点。若四边形CDEF为正方形，求正方形边长。

改编策略二：同时否定多个条件，如改变图形的形状，或改变图形的数量等。

例 3：在△ABC 中，∠C=90°,AC=4,BC=3。

图16　

图17　

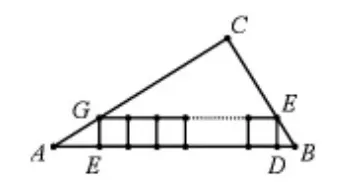
图18　

（1）如图16，在△ABC内部，并排两个相同的正方形，它们组成的矩形内接于△ABC，求正方形的边长；（2）如图17，在△ABC内部，并排三个相同的正方形，它们组成的矩形内接于△ABC，求正方形的边长；（3）如图18，在△ABC内部，并排n个相同的正方形，它们组成的矩形内接于△ABC，求正方形的边长。

例 4：如图 19，在 Rt△ABC 中有边长分别为 a，b，c的三个正方形，∠C为直角，求a，b，c满足的关系。（烟台中考）

图19　

例 5：已知 Rt△ABC 中，∠ACB＝90°，AC＝6，BC＝8。

如图20，若半径为r的⊙O是Rt△ABC的内切圆，求r。

图20　

例6：一张等腰三角形纸片，底边长13cm，底边上的高为32．5cm，现沿底边依次从下往上裁剪宽度均为5cm的矩形纸条，如图21所示。已知剪得的纸条中有一张是正方形，则这张正方形纸条是第几张？（温州中考）

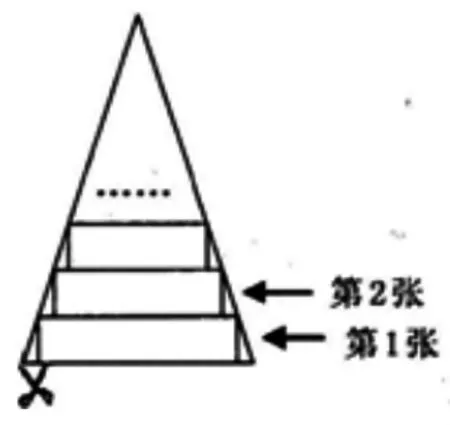
图21　

改编策略三：整合多个例题。

例 7：整合例 1和例 5，如图 22，四边形 PQRS为Rt△ABC 的内接矩形，∠ACB＝90°，三个内切圆的半径从小到大依次为r1,r2和r3。当内接矩形的面积达到最大时，求r1,r2,r3满足的数量关系。

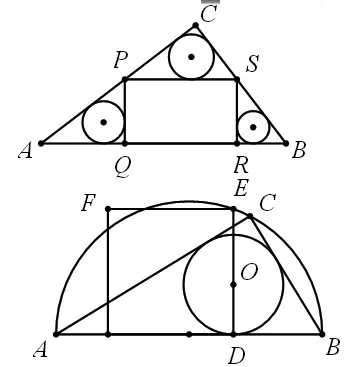
图22　

例8：整合例2和例5，如图23，AB为半圆的直径，C是半圆弧上一点，正方形DEFG的一边DG在直径AB上，另一边DE过ΔABC的内切圆圆心O，且点E在半圆弧上。（1）若正方形的顶点F也在半圆弧上，则半圆的半径与正方形边长的比是______；（2）若正方形DEFG的面积为100，且ΔABC的内切圆半径r=4，则半圆的直径AB=______。（杭州中考）

图23　

一道练习通过否定条件、题组整合等多种形式的改编，运用在课堂教学中，促使学生对初中数学知识的融会贯通，创建学生自主建模的能力，培养学生掌握数学思想与方法，培养学生思维的灵活性、深刻性和创造性，提高学生的数学素质，增强学生解题技巧。

3成效与反思

自从开展本课题研究以来，我们都积极尝试着自己编出几道题，很高兴、很管用。至今，已编出一套非常适用本校教学的习题集，所编的题在多种重大考试中使用，命题质量受到同行好评。

那么，怎样才能改编出好题呢？笔者认为还需要做到以下三点：（1）加强对题目的记忆，好题可以收集，它是编题的素材；（2）多解题，多思考，提高敏锐性，关注各种题目之间的联系；（3）关注学生的错误，难题、易错题改编价值更高。

通过例习题改编，对现行教材进行大胆处理，真正开辟了一条轻负高效的好路子。我校是自主学习的特色学校，近年来积极参与新课程改革，推行先学后教的教学新范式，本课题的研究，也符合数学学科在课程改革中的要求，坚持了一年多的团队实践，不仅改变了我们课题组老师的教学方式，而且还收集整理了一份以教材改编为主的学案集，极大地提高了我们的教学质量。我们任教的年级，在各级各类比赛考试中，各项指标都远超片常模。

数学新课程改革是一个在探索中发展的过程，需要所有数学教育工作者的共同努力。今后，在课堂新范式的推进、数学教材的处理、数学试题的改编过程中，我们将继续和其他同行一起，深入研究教学问题，扩大实验成果。本课题的研究与实施，已经变革了我们课题组老师的的教学方式，并且我们也从中获益不少，值得我们继续为之努力。

[1]李志敏.如何设计新题[J]．数学通报，2010(8)：37-40.

[2]潘超．变有限意无穷——谈基于“几何画板”的变式探究[J]．中学数学教学参考:初中版，2012(11)：47－49.

[3]沈雪明．用课本例题解竞赛题例说[J]．中等数学，2005(10)：13-14.

[4]黎奇.新课程背景下的有效课堂教学策略[M].北京：首都师范大学出版社，2010.