供应链成员渠道选择行为博弈研究
孙军艳, 吴冰莹, 夏 田, 傅卫平
(1.陕西科技大学 机电工程学院, 陕西 西安 710021;2.西安理工大学 机械与精密仪器工程学院, 陕西 西安 710048)
随着市场竞争日益激烈,产品同质性越来越强,且同类产品在性能上的差距越来越小,企业的竞争力已不仅仅体现在产品的性能、价格上,销售渠道也是影响企业竞争力的重要因素。随着消费模式的网络化和多样化,越来越多的企业采用线上与线下将结合的方式设计销售渠道。Kabadayi[1]研究表明企业采用线上直销与线下分销相结和的渠道(以下简称“双渠道”)销售策略可以最小化交易成本,最大化利润,证明了双渠道销售的可行性。在这种情况下,研究如何引导供应商成员自主地选择双渠道,以及如何获取自身的最大效益具有重要的意义。
事实上,很多因素如渠道成本、补偿方式和协调机制等影响着供应链上下游双方对渠道的选择。董志刚等[2]分别建立了双渠道供应链中以制造商为主体和以电商分销商为主体的博弈模型,发现制造商对分销渠道的选择主要受分销渠道成本的影响。仲凯旋等[3]和张学龙等[4]都发现零售商需要给予制造商一定的补偿费用才能解决双渠道存在的双重边际效应,实现双渠道供应链的协调。汪源等[5]提出了制造商和零售商采用价格补偿或成本分摊的协调方式都有利于供应链优化。Amrouche等[6]发现网络渠道收益分配机制是协调渠道的关键因素。赵礼强等[7]根据双渠道的需求函数建立了制造商和零售商的博弈模型,发现制造商可以通过调整定价实现渠道协调,但这种协调方式导致制造商利益受损。
在双渠道策略下,部分学者研究供应链成员如何定价以保证自身和供应链整体的利润最大化。周永卫等[8]建立了以零售商为主体的双渠道供应链收益模型,发现需求的不确定性会影响渠道定价。梁喜等[9]建立价格与需求相关的需求函数,对比制造商Stackelberg博弈和制造商与零售商Bertrand博弈下的最优定价问题,发现在Bertrand博弈决策模式中的制造商在传统渠道的价格最高,在网络渠道的价格最低。Hua等[10]发现了到货支付时间对零售商和制造商的需求、定价策略及利润有较大影响。
本文综合考虑渠道成本分配和收益分配对渠道选择行为的影响,建立更全面反映实际情况的制造商和零售商两阶段博弈模型,分析各影响因素对供应链博弈双方渠道选择行为的影响。以此为基础,在双渠道策略下,分析到货支付时间对供应链成员定价的影响。该研究有助于供应链成员合理理性的选择双渠道,并在双渠道下制定最优的价格策略。
1 问题的描述和基本假设
本文考虑建立由一个制造商和一个零售商组成的两阶段供应链模型,制造商负责产品的研发和制造,零售商可通过分销商向制造商购买产品并在市场中销售,也可以通过制造商的网络渠道直接购买产品并在市场中销售,但因制造商或零售商选择网络渠道后会对分销商产生一定的影响,因此必须给予分销商相应的补偿。通过以上描述,可引出本文研究的问题:制造商和零售商如何选择最适合自身的销售渠道并制定产品的价格?为便于描述和分析问题,提出以下基本假设。
假设1制造商采用双渠道策略的概率为p,采用传统渠道策略的概率为1-p。零售商采用双渠道策略的概率为q, 采用传统渠道策略的概率为1-q。
假设2M为制造商和零售商选择网络渠道后所得收益。其中制造商所得收益为αM,满足0<α≤1,则零售商所得收益为(1-α)M。MM和MR分别为制造商和零售商在传统渠道所得收益。
假设3C为制造商或零售商选择网络渠道后对分销商的补偿成本。若制造商和零售商都选择双渠道进行销售和购买行为,则需要通过协商来划分对分销商的补偿成本。其中制造商所付出的补偿成本为βC,满足0<β≤1,则零售商所付出的补偿成本为(1-β)C。只有制造商选择双渠道策略而零售商不选择时,则需要承担全部对分销商的补偿成本,即β=1;反之,β=0。
根据现实,只有当供应链中网络收益M大于对分销商的补偿成本C,且制造商和零售商所付出的补偿成本小于或等于其各自获得的超额收益,即αM-βC≥0,(1-α)M-(1-β)C≥0,制造商和零售商才会选择双渠道策略。分散决策下的制造商和零售商独自决策,并以自身利益最大化为目标,其博弈收益函数见表1。

表1 制造商与零售商的利润矩阵Tab.1 Profit matrix between manufacturer and retailer
2 制造商-零售商渠道选择行为分析
pC+pqC+MM-E1
(1)
qC-MR-E2
(2)
根据演化博弈理论,可构建制造商和零售商选择双渠道销售时所得的复制动态方程:
p(1-p)(qαM-qβC-C+qC)
(3)
q(1-q)[p(1-α)M+pβC-C]
(4)
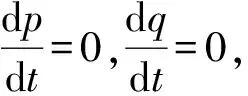
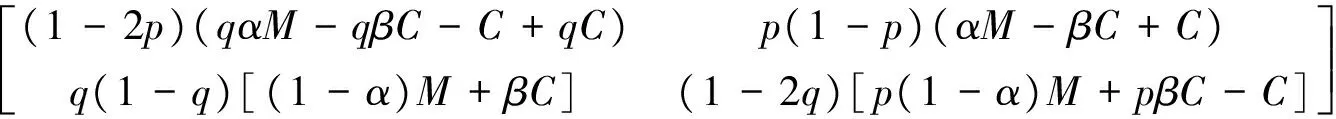
(5)
根据Jacobi矩阵的Det和Tra来判断均衡点的局部稳定性,当且仅当Det>0和Tra<0时,该均衡点为ESS稳定。故分别对每一个均衡点求Det和Tra,可得点(0,0)和(1,1)是该博弈的演化稳定策略,点(0,1)和(1,0)是该博弈的演化不稳定策略,(PD,QD)是鞍点,见表2。
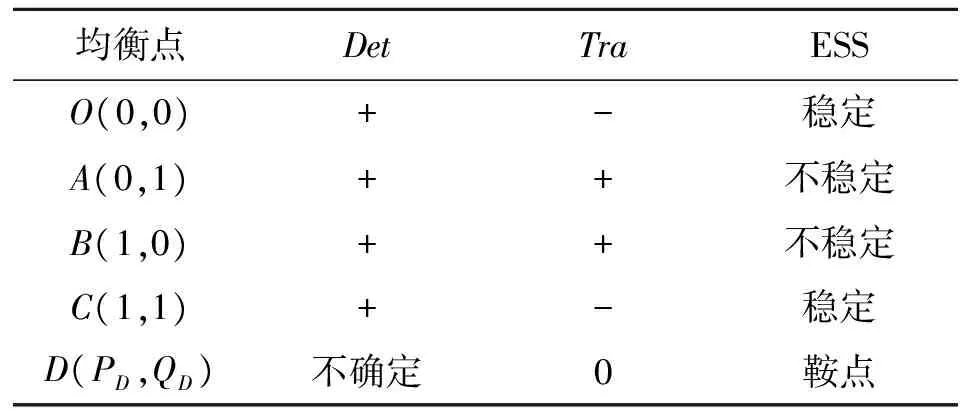
表2 均衡点的局部稳定性分析Tab.2 Local stability analysis of equilibrium point
演化博弈相图见图1。

图1 演化博弈相图Fig.1 Evolutionary game phase diagram
3 考虑制造商和零售商是否选择双渠道决策
演化是一个动态过程,博弈收益矩阵中的各个影响因素都会影响到最终的演化路径和结果。由图1可知,制造商和零售商的稳定策略为(双渠道,双渠道)和(传统渠道,传统渠道),并且最终演化结果取决于四边形OADB和四边形ADBC的面积大小。当SOADB>SADBC时,制造商和零售商选择传统渠道策略的概率大于双渠道策略;反之,则是选择双渠道策略的概率大于传统策略;当SOADB=SADBC时,制造商和零售商选择双渠道策略和传统渠道策略的概率相同。通过分析四边形ADBC面积可得博弈矩阵中各个影响因素对演化路径和结果的影响。由图1可知,四边形ADBC面积为:
(6)
1)对分销商的补偿成本C和网络渠道收益M对演化结果的影响。对SADBC求关于补偿成本C和网络渠道收益M的一阶偏导数,得∂SADBC/∂C<0,∂SADBC/∂M>0,故SADBC是关于C的单调减函数,是关于M的单调增函数。随着补偿成本C的增加,SADBC逐渐减少,系统向点O(0,0)演化的概率增加;随着网络渠道收益M的增加,SADBC逐渐增加,系统向点C(1,1)演化的概率增加。
结论1:对分销商的补偿成本C越小,供应链的网络渠道收益M越大,制造商和零售商选择双渠道策略的概率越大。


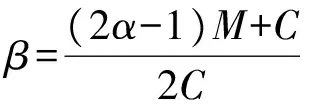
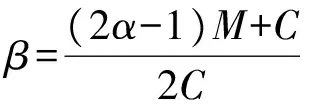
4 考虑到货支付时间的最优定价策略
上文讨论了制造商-零售商双渠道选择的博弈收益矩阵,发现网络渠道收益及其分配系数、对分销商的补偿成本及其分配系数都对制造商和零售商的渠道选择行为有影响,下面进一步讨论当制造商和零售商都选择双渠道策略时,到货支付时间对制造商和零售商最优定价的影响。供应链结构见图2。
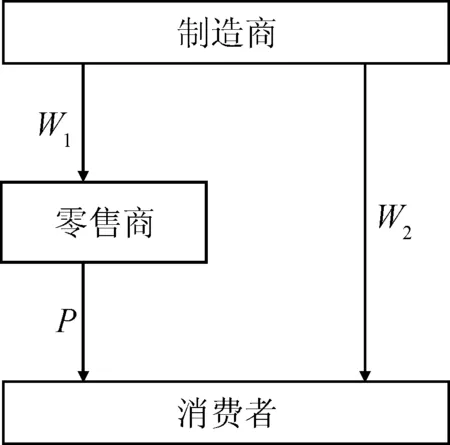
图2 双渠道供应链结构Fig.2 Structure of dual channel supply chain
基于上文假设,用下标“1”表示传统渠道,用下标“2”表示网络渠道,令C0为制造商的制造成本,P为零售商产品售价,W为制造商的批发价,T为到货支付时间。考虑常见的线性需求函数,设传统渠道和网络渠道的市场需求分别为d1=(1-λ)a-T1P+T2W2和d2=λa-T1W2+T2P。其中,di,a,λ,Ti均大于0,0<λ<1。a表示市场份额,λ表示网络渠道所占的市场份额,则传统渠道所占市场份额为1-λ。由于需求量主要受到价格和到货支付时间影响。根据现实,渠道所需的物流环节越多,到货支付时间越长,必然会影响渠道的需求量。用Ti表示渠道需求的敏感系数,需满足T2 制造商和零售商在选择双渠道策略后,势必要做出价格决策,本文分别从制造商Stackelberg、零售商Stackelberg和双方Nash博弈这3种情况下分析双方的定价策略。ΠM,ΠR分别表示制造商和零售商的利润。 1) 制造商Stackelberg的定价策略 当制造商占主体地位时,制造商先确定传统渠道和网络渠道的批发价W1和W2,零售商再确定产品售价P。零售商的利润为ΠR=(P-W1)d1。由于ΠR的Hessian矩阵负定,由一阶最优条件可得最优定价为: (7) (8) (9) 2) 零售商Stackelberg的定价策略 当零售商占主体地位时,零售商先确定产品售价P,制造商再确定传统渠道和网络渠道的批发价W1和W2,其利润为ΠM=W1d1+W2d2。由于ΠM的Hessian矩阵负定,由一阶最优条件可得最优定价为: (10) (11) 当零售商得到制造商的最优定价后,决定售价P,零售商的利润为ΠR=(P-W1)d1。因d2ΠR/dP2<0,由一阶最优条件可得最优定价为: (12) 3) 双方Nash博弈的定价策略 (13) (14) (15) 由于前文有较多的参数和变量,且推导后的数学公式较为复杂,故采用数值仿真分析方法来更直观的分析制造商和零售商选择双渠道的变化情况。根据前文的假设条件,不失一般性地给参数赋值,见表3。当探讨某参数对渠道选择概率的影响时,只需改变该参数的取值范围即可。 表3 参数赋值表Tab.3 Parameter assignment table 1) 制造商和零售商是否选择双渠道策略取决于为达成双渠道策略所需付出协调成本及达成双渠道策略后获得的额外收益。保持其他参数不变,令C以步长50从0变化至1 000,M以步长50从0变化至1 000,根据参数计算SADBC的变化情况,见图3。 图3 C和M对制造商和零售商选择双渠道策略的影响Fig.3 The impact of C and M on manufacturer and retailer’s choice of dual channel strategy 由图3可知,随着协调成本C的增加,SADBC函数图像单调递减,制造商和零售商选择双渠道的概率也随之减小;随着额外收益M的增加,SADBC函数图像快速增长并趋于平缓,说明当制造商和零售商意识到达成双渠道策略会获得的额外收益时,双方选择达成双渠道策略的概率大幅增加,但随着额外收益的持续增加,双方选择双渠道的概率会逐渐趋于平稳。结论1得以验证。 2) 制造商和零售商是否选择双渠道策略还取决于双渠道策略所需付出协调成本分配系数及达成双渠道策略后获得额外收益的分配系数。保持其他参数不变,令α以步长0.05从0变化至1,β以步长0.2从0变化至1,计算SADBC的变化情况。图4表示α和β对制造商和零售商选择双渠道策略的影响。 图4 α和β对制造商和零售商选择双渠道策略的影响Fig.4 Impact of α and β on manufacturer and retailer’s choice of dual channel strategy 由图4可得,在β的不同取值下,SADBC函数图像都呈“倒U型”,说明存在一个最优的α值,使得SADBC取极大值,即制造商和零售商选择双渠道策略的概率最大。当α<0.5时,β越大,SADBC越小,说明制造商分得的额外收益越小且承担的协调成本越多,系统演化到双方选择双渠道策略的概率越小;反之,当α>0.5时,β越大,SADBC越大,说明制造商分得的额外收益越大且承担的协调成本越少,双方选择双渠道策略的概率越大。这也说明,只有当博弈双方得到的超额收益和付出的协调成本成比例时,双方才会选择双渠道策略。结论2、3得以验证。 3)传统渠道的到货支付时间对不同决策模式下制造商和零售商最优定价策略的影响,保持其他参数不变,令T1以步长1从11变化至101,计算不同决策模式下制造商和零售商的最优定价,见图5。 图5 不同决策模式下制造商和零售商最优定价Fig.5 Optimal pricing of manufacturers and retailers under different decision models 由图5可得,随着T1的增加,W1、W2和P逐渐减少,说明价格与传统渠道的到货支付时间负相关;以制造商为主体时供应链成员的价格最高,以零售商为主体时供应链成员的价格次之,双方地位均衡时供应链成员的价格最低。 以制造商为主体的供应链中,当T1∈(11,29)时,W2 以零售商为主体的供应链中,制造商在传统渠道的批发价W1始终最小,且存在一个临界值T1=19,当小于临界值时,制造商在网络渠道的批发价W2小于零售商售价P,消费者更倾向于网络渠道购买;当大于临界值时,则相反,消费者更倾向于传统渠道购买。 在双方地位平等的供应链中,P>W2>W1,且W1和W2的差值始终为1,说明传统渠道的到货支付时间对制造商在传统渠道和网络渠道批发价的影响相同。 本文从制造商和零售商的渠道选择行为和定价策略两方面对供应链成员进行了两阶段博弈分析。首先分析了供应链成员渠道选择行为的因素,建立了供应链中制造商和零售商渠道选择的博弈矩阵,以此为基础,分析了到货支付时间对不同决策模式下双方定价的影响。 1) 网络渠道收益的增加、对分销商补偿成本的降低以及合理的网络渠道收益分配系数和补偿成本分配系数将有利于制造商和零售商的选择向双渠道策略演化。 2) 在双渠道下,传统渠道到货支付时间的增加会降低制造商的传统渠道批发价、网络渠道批发价和零售商售价。 3) 在双渠道下,以制造商为主体或以零售商为主体时,存在一个传统渠道到货支付时间的临界点,当小于临界点时,制造商在网络渠道的批发价小于零售商售价,消费者更倾向于网络渠道购买;当大于临界点时,制造商在网络渠道的批发价大于零售商售价,消费者更倾向于传统渠道购买。在双方地位平等的供应链中,消费者更倾向于网络渠道购买。 4) 在双渠道下,以制造商为主体时供应链成员价格最高且制造商在网络渠道的批发价最高,以零售商为主体时供应链成员的价格次之,双方地位均衡时供应链成员的价格最低。由此可得,集中型供应链的总体收益高于分散型供应链。 参考文献: [1] KABADAYI S. Choosing the right multiple channel system to minimize transaction costs [J]. Industrial Marketing Management, 2011, 40(5): 763-773. [2] 董志刚, 徐庆, 马骋. 电子商务环境下双渠道供应链的制造商分销渠道选择 [J]. 系统工程, 2015, 33(6): 26-33. DONG Zhigang, XU Qing, MA Chi. Manufacturers’ selection of distribution channels in dual-channel supply chain based on electronic commerce [J]. Systems Engineering, 2015, 33(6): 26-33. [3] 仲凯旋, 巩永华, 薛殿中. 零售商双渠道供应链定价及协调研究 [J]. 南京邮电大学学报(社会科学版), 2015, 17(4): 46-51. ZHONG Kaixuan, GONG Yonghua, XUE Dianzhong. On pricing and coordination strategy of retailers’ dual channel supply chain [J]. Journal of Nanjing University of Posts and Telecommunications(Social Science), 2015, 17(4): 46-51. [4] 张学龙, 王军进. 制造商主导型双渠道供应链协调决策模型 [J]. 控制与决策, 2016, 31(8): 1519-1525. ZHANG Xuelong, WANG Junjin. Supply chain coordination decision model of manufacture-led dual-channel supply [J]. Control and Decision, 2016, 31(8): 1519-1525. [5] 汪源. 考虑服务溢出因素的双渠道供应链服务策略研究 [J]. 物流科技, 2015, 38(2): 10-14. WANG Yuan. Study on coordination strategies of dual-channel supply chain with service spill-over effect [J]. Logistics Sci-tech, 2015, 38(2): 10-14. [6] AMROUCHE N, YAN Ruiliang. A manufacturer distribution issue: how to manage an online and a traditional retailer [J]. Annals of Operations Research, 2015, 244(2): 1-38. [7] 赵礼强, 徐家旺. 基于电子市场的供应链双渠道冲突与协调的契约设计 [J]. 中国管理科学, 2014, 22(5): 61-68. ZHAO Liqiang, XU Jiawang. Contract design for coordination conflict of dual channels supply chain based on e-market [J]. Chinese Journal of Management Science, 2014, 22(5): 61-68. [8] 周永卫, 范贺花. 随机需求与联合促销下双渠道供应链定价策略 [J]. 统计与决策, 2015, (18): 51 -55. [9] 梁喜, 郭瑾. 网上代销双渠道闭环供应链的定价与协调决策 [J]. 商业研究, 2017,(2): 1-11. LIANG Xi, GUO Jin. Pricing and coordination strategy of online agent selling dual channel closed-loop supply chain [J]. Commercial Research, 2017,(2): 1-11. [10] HUA Guowei, WANG Shouyang, Cheng T C E. Price and lead time decisions in dual-channel supply chains [J]. European Journal of Operational Research, 2010, 205(1): 113-126.
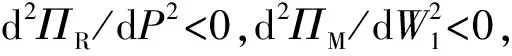
5 算例分析




6 结 论

