基于图像掩模和击中击不中变换的优化边缘提取算法

陈恺煊, 刘　昕, 王　咚

(西安理工大学 印刷包装与数字媒体学院, 陕西 西安 710048)

边缘是指图像上像素灰度值突变的地方,是图像最基本的特征。边缘检测的目的是在有噪声背景的图像中确定出目标物边界的位置,这在很大程度上减少了所要处理的信息量,但同时又保留了图像中物体的形状信息,使图像分析过程大大简化。边缘检测技术在医学图像处理领域(如细胞图像分析)有着广泛的应用,除此之外,它也是机器视觉、模式识别等领域的重要基础。

在边缘检测算法中,Sobel算法因其计算简单、速度快而被广泛应用,但同时存在着漏检边缘、抗噪能力差、边缘线条较粗等问题,只能满足精度不高的检测需求。国内外许多学者也做了相关研究。文献[1]在传统Sobel算法上构造出一种8方向的5×5检测模板,增强了算法的抗噪性,但计算耗时较长,并且会导致边缘线条较粗。文献[2]在得到边缘梯度图后,采用局部处理法对边缘图像进行细化,有一定的细化效果,但并未排除图像中的干扰点,而且局部处理算法本身过于复杂。文献[3]使用双阈值法对边缘梯度图像进行分割,与传统算法相比,有一定的细化效果,但边缘存在断裂,丢失了很多细节。文献[4]对图像先使用Otsu算法进行二值化,然后通过数学形态法去除孤立像素干扰点,提高了算法在检测方向的准确性,但没有从灰度的角度将图像的前景和背景分离,而且闭运算会导致图像细节的丢失。

1　传统的Sobel边缘提取算法

传统Sobel算子由两个大小为3×3的模板构成,如图1所示。模板中的系数和为零,说明在灰度级不变的区域,模板响应为零。

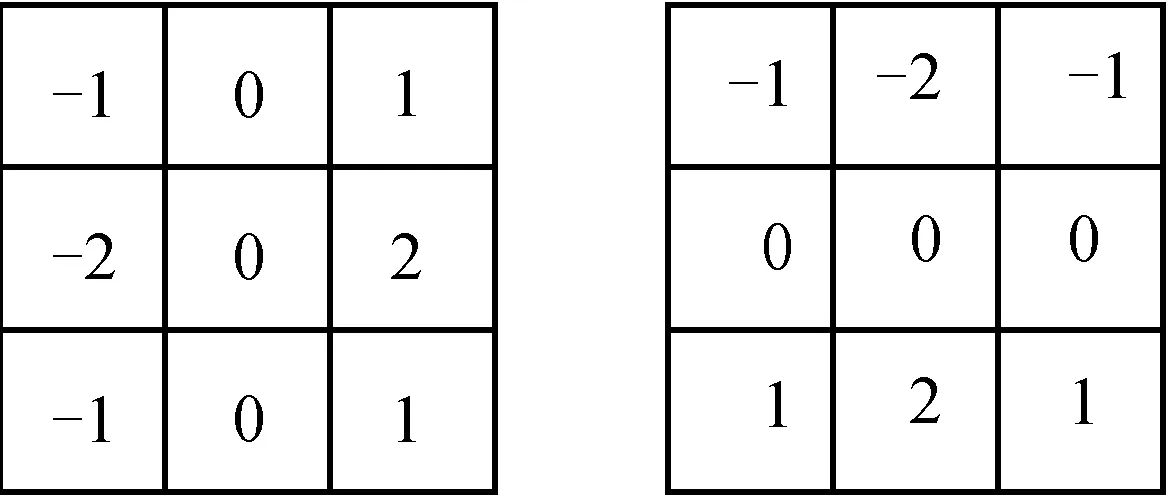
图1　Sobel算子的两个方向模板Fig.1　Direction templates of Sobel operator

让两个方向模板分别沿着x轴、y轴与图像做卷积,方向是从上到下和从左到右,将模板的中心和图像上的某个像素重合,并将该像素周围的点与模板上对应的系数相乘,假设图像上某一区域的像素点如图2所示。

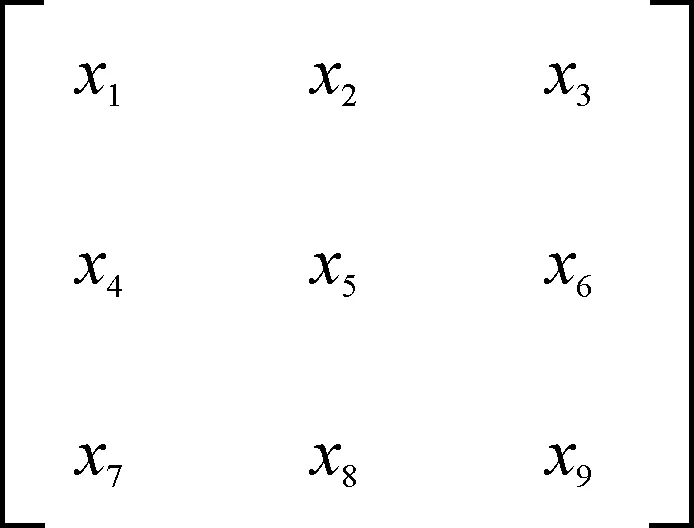
图2　图像某一区域的像素点Fig.2　Pixels in a region of the image

则该中心点x轴、y轴方向上的梯度分量分别为:

f0°=(x3+2x6+x9)-(x1+2x3+x5)

(1)

f90°=(x7+2x8+x9)-(x1+2x2+x3)

(2)

最终,该中心点的梯度大小可由横向及纵向灰度值求得,即:

(3)

由于平方和平方根运算计算量较大,一般使用绝对值对梯度[5]进行近似处理,在保持灰度级相对变化的同时,节省计算时间:

f≈|f0°|+|f90°|

(4)

Sobel算子的边缘提取方法计算简单、速度快,而且相比Prewitt算子,Sobel算子的中心使用权值2[6],即通过增加中心点的重要性,实现了一定程度的平滑,从而更好地抑制了噪声。但也存在边缘定位精度不高的问题,容易漏检边缘,同时会出现伪边缘,使边缘线条较粗,无法用来检测纹理复杂的图像。

2　改进的Sobel边缘提取算法

2.1　改进算法的技术路线

改进后算法的步骤如图3所示。首先对原始图片进行预处理,即将图片先灰度化,然后利用中值滤波进行平滑去噪,以减少运算量,并消除孤立噪声点的干扰。

然后,在传统Sobel算法的基础上增加两个方向模板,利用四个方向模板进行准确定位,从而使得对于纹理复杂的图像,也能得到完整的边缘梯度图。

接着进行边缘细化,对梯度图像进行边缘检测,用得到的双线条边缘图像制作掩膜,并将掩膜覆盖在梯度边缘图像上,即通过原始边缘图像与双线条边缘图像相减,来进行细化。重复此细化步骤,将细化后的边缘梯度图再次与其双线条图像相减,以完成第二次细化。

最后,将经过两次细化的边缘梯度图利用Otsu算法进行二值化,并利用数学形态中基于击中击不中变换的细化来对图像进行全局处理,以消除因复杂纹理产生的干扰像素点。

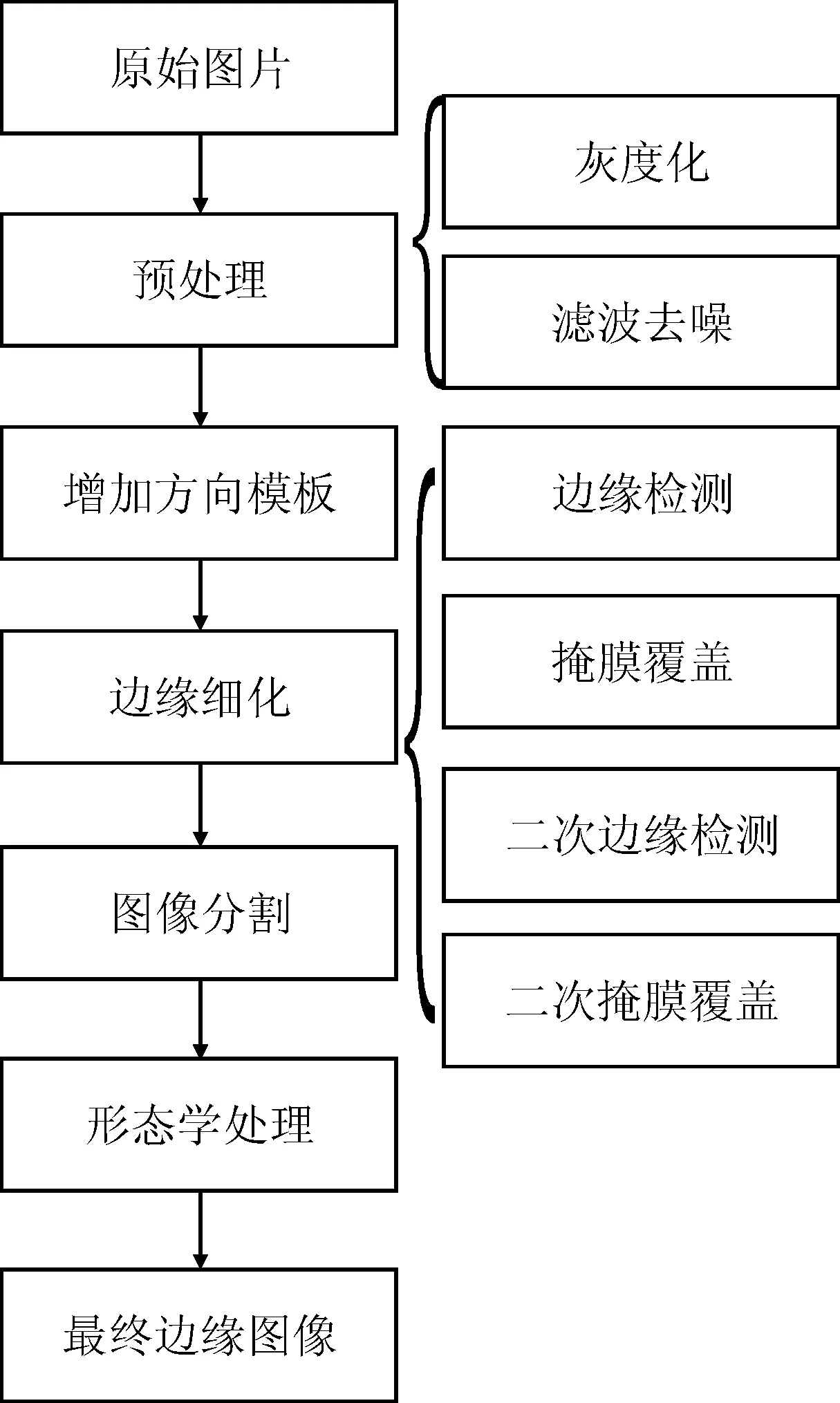
图3　改进边缘提取算法的技术路线图Fig.3　Steps of improved edge detection algorithm

2.2　方向模板的增加

由于传统的Sobel算子只有0°和90°两个方向模板,只对水平和垂直方向的边缘有响应,可以满足简单图像的边缘检测要求,为了能检测纹理更加复杂的图像,需要增加Sobel算子的方向模板,如图4所示,分别添加45°和135°两个方向模板。

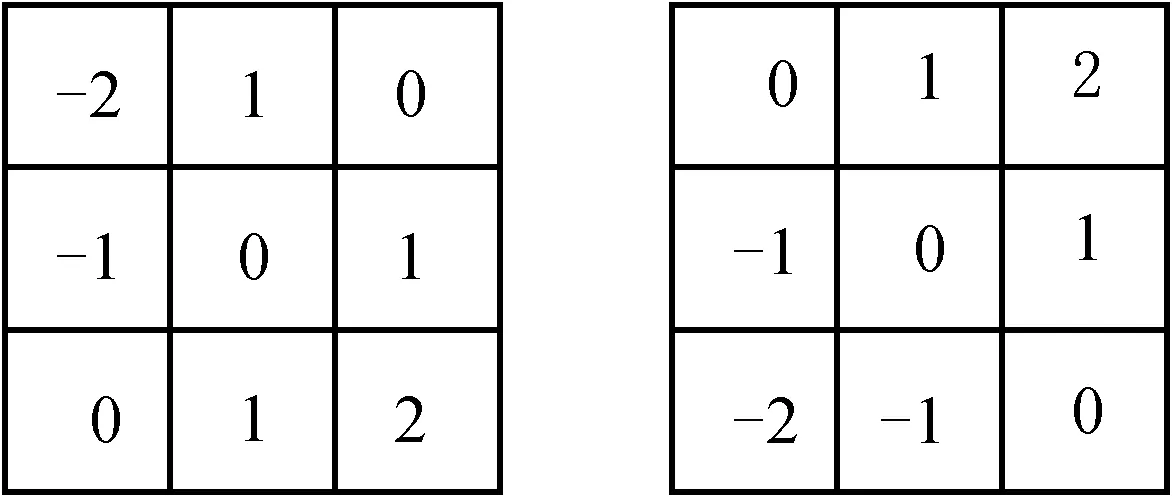
图4　45°和135°的方向模板Fig.4　Direction templates at 45°and 135°

图像边缘在45°和135°的梯度分量分别为:

f45°=(x6+x8+2x9)-(2x1+x2+x4)

(5)

f135°=(x2+2x3+x6)-(x4+2x7+x8)

(6)

最终所对应的图像上的点的梯度值为:

f≈|f0°|+|f45°|+|f90°|+|f135°|

(7)

该算法增加了两个方向模板,能检测出对角线方向上的边缘,即可使算子在0°、45°、90°、135°四个方向都有响应,使边缘定位更加准确,与传统Sobel算子相比,可在不明显增加运算时间的前提下,提取到更完整的边缘信息。

2.3　边缘的细化

在增加方向模板后的梯度图像中,边缘线条很粗,为了得到效果更好的边缘图像,需要对线条进行细化处理。

引起边缘线条过粗的原因有两个:首先,在图像的各个区域之间,边缘的梯度值变化在理想状态下会形成阶跃,如图5(a)所示,而现实情况中,边缘的梯度值变化并不是理想的,而是大多呈现一种屋顶状,如图5(b)所示。可以将边缘及其附近的梯度值分为暗部、灰部和亮部,真实边缘位于暗部处,灰部则是边缘和非边缘之间的过渡部分,它会对边缘线宽产生影响,使线条变粗。

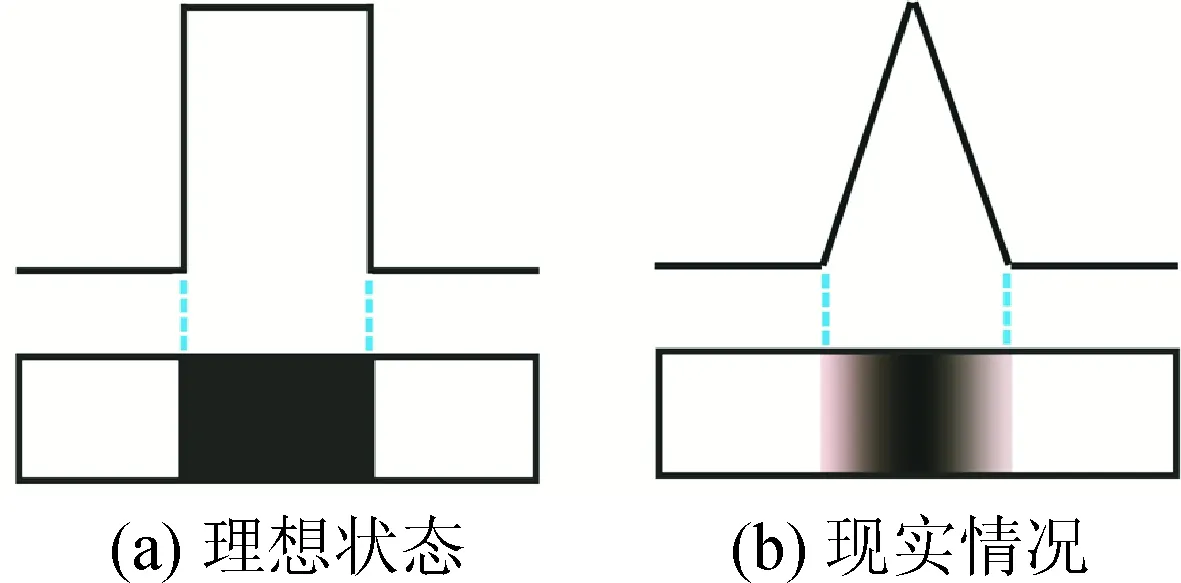
图5　阶梯状边缘灰度变化Fig.5　Step edge gray scale change

其次,因为图像边缘两侧点的梯度值会在某一方向产生变化,Sobel算子正是利用点的这种变化来进行判断,所以在检测时,这些沿着真实边缘的连续的点也会被识别为边缘,这就是伪边缘。伪边缘位于真实边缘两侧,会使真实边缘变粗,如图6所示。在增加45°和135°两个斜向模板后,这种现象会更为明显。

在用边缘检测算子对图像进行检测得到的灰度图像中,将检测结果的边缘轮廓线视为高灰度区域,这个灰度区域同时包括伪边缘和真实边缘,若能对这个区域进行收缩,即对线条的宽度进行缩减,就可以实现边缘的细化。

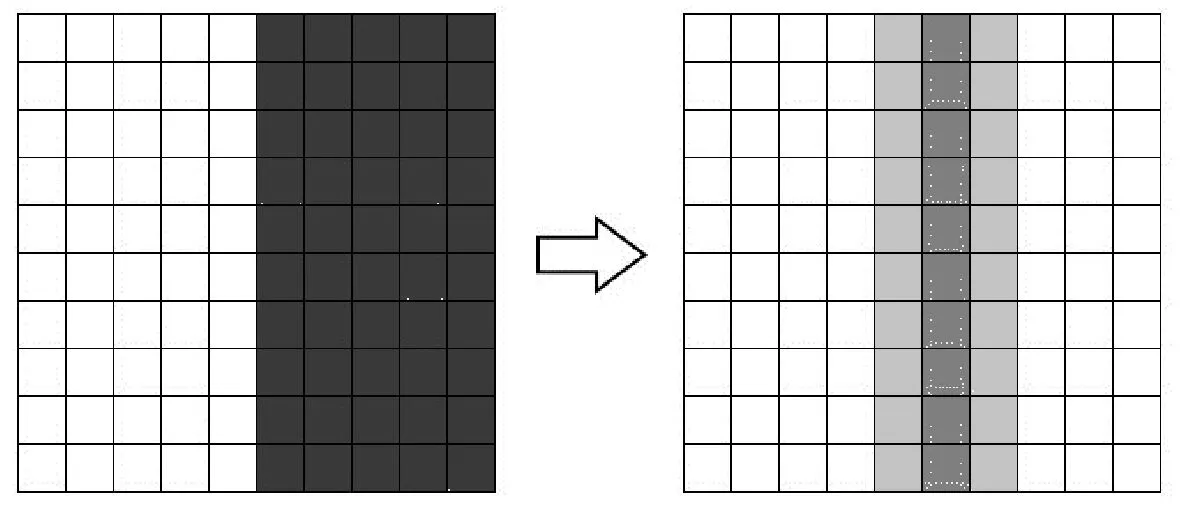
图6　真实边缘和伪边缘Fig.6　Real edge and false edge

对边缘的细化如图7所示。用图7(a)与方向模板卷积,假设得到边缘检测结果S1,如图7(b)所示,S1包括真实边缘和伪边缘。对S1再进行一次边缘检测,得到一副双线条的边缘图像,如7(c)所示,设为S2。利用S2作为掩膜,对S1进行覆盖,因为双线条所在区域和伪边缘重合,从S1中去除S2的高灰度区域,即用S1减去S2,就可以减少线宽,从而细化边缘,结果如图7(d)所示,设为S3。

图7　边缘的细化Fig.7　Edge thinning

若对S3重复细化步骤,即再次对其进行边缘检测,并用双线条图像与S3相减,可以将S3中的边缘进一步细化。理论上讲,可以对边缘进行多次细化,但是值得注意的是,连续进行边缘细化是以损失图像细节为代价的,所以必须控制细化的次数,来保证边缘图像的细节。

2.4　基于Otsu算法的图像分割

Otsu算法也称最大类间方差分割法或大津阈值分割法。基本思想是根据阈值对像素进行划分,通过划分使得到的目标类与背景类产生最佳的分离性能,而此性能用类间方差来[7]表征。

对一幅图像,将其按照灰度级分为前景和背景,设T为前景与背景的分割阈值,前景点数占总图像比例为w0,平均灰度值为u0;背景点数占总图像比例为w1,平均灰度为u1,则图像的总平均灰度为:

u=w0×u0+w1×u1

(8)

定义类间方差为:

σ2=[w0×(u0-u)2+w1×(u1-u)2]

(9)

从最小灰度值到最大灰度值遍历T[8],当T使得类间方差最大时,即为分割的最佳阈值。因类间方差是灰度分布均匀性的一种度量，类间方差值越大说明构成图像的两部分差别越大,当部分目标错分为背景或部分背景错分为目标时,都会导致两部分差别变小,因此,使类间方差最大的分割,意味着错分概率最小。

直接应用式(9)会导致运算量增大,为了减少运算量,在日常应用时,采用等价公式:

g=w0×w1×(u0-u1)2

(10)

传统Sobel算子的缺点之一是并没有将图像的主题与背景严格地区分开来,换言之,就是没有基于图像灰度进行处理,由于Sobel算子并没有严格地模拟人的视觉生理特征,所以提取的图像轮廓有时并不能令人满意。而Otsu算法不受图像亮度和对比度的影响,它通过阈值将前景和背景分离开来,很好地克服了此缺点。

2.5　基于击中击不中变换的形态学处理

形态学上的击中击不中变换[9]是形状检测的基本工具,若想在图像A中找到B形状的目标,首先建立一个比B大的模板X,使用此模板对图像A进行腐蚀,得到Set1。然后对模板X进行取反,并用得到的新模板对图像A的补集进行腐蚀,得到的图像为Set2。最后使Set1和Set2取交集,得到的结果就是B的位置,即:

A*B=(AΘX)∩[AcΘ(W-X)]

(11)

式中,A*B表示B在A中的匹配;

Θ表示腐蚀运算;Ac是A的补集;W是模板X的全集。

基于击中击不中变换的细化,可以通过结构元素消除指定的匹配模式对象,从而改变物体的形状。图8为形态学细化所用的结构元素。图中的结构元素对于去除背景上的单像素孤立点以及边缘上的直角对象非常有用。

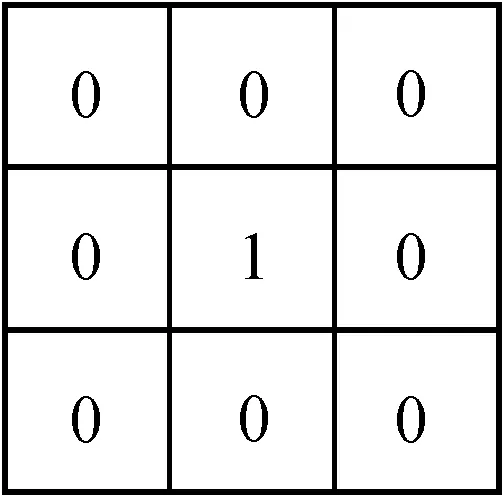
图8　形态学细化所用的结构元素Fig.8　Structure elements of morphological thinning

细化函数提取原始图像与其转换图像的交集,其转换函数是通过击中击不中函数得到的。在二值关系中,此操作是从原始图像中减去击中击不中变换后图像得到的,设I为原始图像,hit·miss(I)为经过变换后的图像,Thin(I)为最后得到的图像,等同于对I和hit·miss(I)进行XOR运算,即:

Thin(I)=I-hit·miss(I)=

XOR(I,hit·miss(I))

(12)

图9为干扰点的消除。如图9(a)所示,图中因人物帽子纹理的关系,产生了很多孤立且离散的干扰点,对于以边缘提取为主要目的的操作,要尽量避免此类干扰点的产生。值得注意的是,在这里,边缘线条已经经过了两次细化,若对其进行先腐蚀再膨胀的开运算来消除孤立干扰点,会将本来就很细的边缘线条腐蚀掉,所以此种方法是不可行的,如图9(b)所示。而对图像利用击中击不中变换进行细化后,整体边缘并未受到影响的同时,还在很大程度上消除了这些孤立的干扰像素点,如图9(c)所示。

图9　干扰点的消除Fig.9　Elimination of interference points

3　实　验

图10　源图像Fig.10　Source images

实验程序利用LabVIEW和MATLAB两种软件进行混合编程,即通过LabVIEW中的MATLAB script节点[10]对MATLAB进行调用,达到处理图片的目的。首先,选取三张美国南加利福尼亚大学图像实验室中的标准图像作为图像来源,如图10所示。对源图像进行平滑去噪和灰度化的预处理后,利用四个方向模板对源图像进行卷积得到边缘梯度图像,如图11所示。

图11　边缘梯度图像Fig.11　Image edge gradient

梯度图像由于伪边缘的原因,存在着边缘线条过粗的现象,需要对其进行细化。首先对梯度图像进行边缘检测,得到双线条掩膜图像,如图12所示。用掩膜对梯度图像进行覆盖,以去除梯度图像中的伪边缘部分,两者进行相减,可以得到第一次细化后的梯度图。若重复此过程,即对一次细化后的梯度图进行边缘检测,并再次利用双线条掩膜进行覆盖,可以得到二次细化后的梯度图。由图12可以看出,和原梯度图(见图11)相比,经过两次细化后的梯度图的边缘线条有了明显的细化,且保持了原图的细节。

图12　边缘细化过程Fig.12　Edge thinning process

对细化后的梯度图像进行基于Otsu算法的二值分割,并利用数学形态中基于击中击不中变换的细化对图像进行全局处理,以去除背景上的单像素孤立点,并平滑边缘,得到最终边缘图像,如图13所示。将采用传统Sobel算法和改进后的边缘提取算法的效果图进行比较,可以看出,改进后的边缘提取算法检测出了更多的边缘,在保持细节的前提下细化了边缘,边缘提取质量整体提高。

图13　传统算法与改进算法效果对比Fig.13　Comparison between the traditional algorithm and the improved algorithm

4　结　语

本文对传统Sobel算法存在的问题做出了分析和改进。针对传统算法边缘定位不准确的问题,采用增加两个斜向模板的方法来得到完整的边缘信息。针对卷积后边缘梯度线条较粗的问题,采用双线条掩膜图像进行覆盖的方法来细化边缘。针对纹理复杂图像中存在干扰点的问题,采用数学形态中基于击中击不中变换的细化对图像进行全局处理。

从实验结果可以看出,改进后的算法相较于传统边缘提取算法,其细化效果有了显著提高。此算法可以有效提高目标识别速度与正确率,因此在机器视觉、车牌识别、人脸识别等领域具有广泛的应用价值。

参考文献:

[1] 武亚沙, 张有会, 邱志宇. 8方向自适应权值Sobel边缘检测算子 [J]. 河北师范大学学报(自然科学版), 2015, 39(4): 294-299.

WU Yasha, ZHANG Youhui, QIU Zhiyu. Adaptive weighted Sobel edge detection operator with eight directions [J]. Journal of Hebei Normal University(Natural Science Edition), 2015, 39(4): 294-299.

[2] 沈德海, 侯建, 鄂旭. 基于改进的Sobel算子边缘检测算法 [J]. 计算机技术与发展, 2013, 23(11): 22-25.

SHEN Dehai, HOU Jian, E Xu. Edge detection algorithm based on improved Sobel operator [J]. Computer Technology and Development, 2013, 23(11): 22-25.

[3] 姜炳旭, 刘杰, 孙可. Sobel边缘检测的细化 [J]. 沈阳师范大学学报(自然科学版), 2010, 28(4): 503 -506.

JIANG Bingxu, LIU Jie, SUN Ke. Refinement of Sobel operator-edge detection [J]. Journal of Shenyang Normal University(Natural Science), 2010, 28(4): 503-506.

[4] 袁春兰, 熊宗龙, 周雪花, 等. 基于Sobel算子的图像边缘检测研究 [J]. 激光与红外, 2009, 39(1): 85-87.

YUAN Chunlan, XIONG Zonglong, ZHOU Xuehua, et al. Study of infrared image edge detection based on Sobel operator [J]. Lasers and Infrared, 2009, 39(1): 85-87.

[5] 冈萨雷斯. 数字图像处理 [M]. 阮秋琦，阮宇智，译. 北京: 电子工业出版社, 2005.

[6] 李捷, 唐星科, 蒋延军. 几种边缘检测算法的比较研究 [J]. 信息技术, 2007，(9): 106-109.

LI Jie, TANG Xingke, JIANG Yanjun. Comparing study of some edge detection algorithms [J]. Information Technology, 2007，(9): 106-109.

[7] 韩慧妍, 韩燮. 形态学和Otsu方法在Canny边缘检测算子中的应用 [J]. 微电子学与计算机, 2012, 29(2): 146-149.

HAN Huiyan, HAN Xie. Application of morphology and Otsu method in Canny edge detection operator [J]. Microelectronics & Computer, 2012, 29(2): 146-149.

[8] 李全勇. 联合变换相关器相关面处理技术研究 [D]. 长春: 长春理工大学, 2007.

LI Quanyong. Research on correlation plane processing technology of joint transform correlator [D]. Changchun: Changchun University of Science and Technology, 2007.

[9] 蔡改贫, 李龙茂, 姜志宏. 基于图像处理的矿石粒度检测系统设计 [J]. 冶金自动化, 2013, 37(6): 63-66.

CAI Gaipin, LI Longmao, JIANG Zhihong. Design of ore particle size measurement system based on image processing [J]. Metallurgical Automation, 2013, 37(6): 63-66.

[10] 柴敬安, 廖克俭, 潘德辉, 等. Labview和Matlab混合编程方法的研究与实现 [J]. 计算机测量与控制, 2008, 16(5): 737-739.

CHAI Jing’an, LIAO Kejian, PAN Dehui, et al. Study and implementation on program method of Labview combined with Matlab [J]. Computer Measurement and Control, 2008, 16(5): 737-739.