流固耦合作用下大型地下厂房围岩稳定性分析

郭双枫, 李　宁,2, 刘乃飞, 吕　高

(1.西安理工大学 岩土工程研究所, 陕西 西安 710048; 2.兰州交通大学 土木工程学院, 甘肃 兰州 730070)

随着我国水能资源的建设和西部开发战略的实施,越来越多的大型水电工程兴建于西部高山峻岭地区。西部地区大多属于高山峡谷和沟谷深切的地形地貌,为修建高势能水电站提供了便利条件,大型地下洞室的围岩稳定性和厂房的渗流问题也因此成为热议话题。国内专家针对上述问题进行了许多开拓性的研究,且获得了行之有效的科研成果[1-4]。但是关于降雨入渗和库水位升降后形成的渗流场以及与应力场耦合作用下地下洞室围岩稳定性的研究成果还不太成熟[5]。因此,如何在力学领域中科学合理地分析渗流场和应力场的耦合作用以及解释耦合现象等问题[6-8],越来越受到相关领域的学者和专家的重视,也是具有重要实际意义的科学研究。

本文针对某大型地下厂房的相关特性开展了一些工作。地下工程最大的特点就是它的赋存环境复杂和工程本身的不确定因素太多,由于这些不确定因素的存在[7],使得每一个地下洞室都拥有各自的特点。该水电站地下厂房的工程规模较大,布局庞杂、断面形状和尺度各异、地质条件复杂、断层交汇,工程环境千差万别,持续降雨和洞室内雨水的入渗影响施工和运行期的安全,更给围岩稳定性评价以及支护处理措施带来一定困难。由于大断层贯穿主厂房,降雨期或地下水在洞室开挖过程中形成的渗流场与应力场之间相互作用、相互影响:水体在岩体运动过程中形成的渗流场会发生改变,它以渗透压力的形式施加于岩体介质。成为外部荷载的渗透压力使得岩土体的应力场重分布,而岩土体位移场、体积应变的变化受应力场的影响较大,岩体内的孔(空)隙比、孔(空)隙率也会随之变化,由于多孔介质渗透系数和裂隙大小的关系,渗透系数必定会发生变化,从而引发渗流场分布出现大的变动。岩土体渗流场和应力场的相互影响结果在力学领域表现了一种双场耦合的平衡关系,并且这种平衡时刻都存在着[8]。

为分析持续降雨后地下水形成的渗流场以及流固耦合作用对地下洞室群围岩稳定的影响,验证横穿断层对洞室的危害性。本文采用流固耦合原理的数值方法[9-10],模拟分析地下洞室群施工开挖的完整过程,并在此基础上,分析并评价应力场和渗流场共同作用下大型厂房的围岩稳定性难题。

1　岩体渗流场与应力场耦合分析的数学模型

渗流场和应力场的相互影响是相辅相成的,岩体中渗流场的变化使得岩体中的渗透力发生变化,由此岩体的位移场的改变又受到应力场重新分布的作用。当前有很多渗流场与应力场耦合分析模型,如双重介质模型、离散裂隙网络模型、等效连续介质模型。但不同的数学模型有其相关的适用范畴和相关理论。本文选取等效连续介质数学模型进行渗流场与应力场耦合分析,即将岩石视为等效连续介质,把裂隙网络中的水流按流量等效原则等效到岩石中去。很多文献[11]中都采用等效连续介质模型模拟渗流场与应力场的耦合作用。

在饱和状态下,岩体介质的变形为线弹性的,渗流连续方程为[12]:

(1)

式中:ΔV=ΔxΔyΔz;ρ为水的密度;n为裂隙率;Vx′、Vy′、Vz′分别为X、Y、Z方向上渗流速度矢量的分量。

通过有限元法求解,渗流场数学模型的有限元矩阵形式为:

(2)

式中:[K]为总渗透矩阵;[S]为贮水矩阵;{Q}为汇(源)项列阵;{H}为水头。

由于水头或降雨变化导致的岩体变形量,如果它的体应变量是Δεv,代入到等效连续介质的数学模型中求解应力场问题。采用有限元求解应力场,其有限元方程的矩阵形式为:

{σ}= [D][{ε}+{Δεv}]

(3)

式中:{σ}为应力矩阵;{ε}为不考虑渗透水压力的应变矩阵;{Δεv}为渗透水压力引起岩体变形的应变列阵; [D]为弹性矩阵。

渗流场水头的变化可能导致岩体的应力状态改变,发生应变;同理,外界荷载或地应力的改变会引起岩体中地下水位的变化。将应变增量和水头压力的改变在式(2)～(3)中相互迭代,便形成了渗流场与应力场耦合分析数学模型:

(4)

式中:Ew为地下水的体积弹性模量;γ为容重。

2　工程概况

2.1　工程背景

某水电站是龙羊峡以上黄河干流湖口～羊曲河段规划梯级的第八座水电站,电站距西宁公路里程369 km。该水电站水库总库容15.02亿m3,最大坝高211 m,装机容量2 200 MW(4台520 MW+1台120 MW),工程规模为一等大(1)型工程。该地下厂房主要由主厂房、主变室、尾水闸、母线洞、尾水洞等洞室组成。其地下厂房埋深约200 m,开挖跨度221.45 m×26.6 m×74.1 m,纵轴线方向NW40°,最大开挖尺寸为28.8 m。岩体主要为较完整～完整块状结构,结构面结合紧密,为中等发育～不发育,围岩为二长岩,围岩类别以Ⅱ、Ⅲ1类为主,部分断层破碎带及裂隙密集为Ⅳ类。主变室及尾闸井位于厚层变质砂岩中,主变室开挖尺寸178.85 m×19.8 m×24.5 m[13]。

2.2　地下水

根据地质勘探及现场观测,洞室内很多地方出现地下水聚集渗流,受断层影响这个地区的地下水有以下明显特性[14]:

1) 地下水集中渗流,沿结构面相交或密集部位流动。

2) 地下水在平洞及洞底附件渗流较明显,大多以渗水或滴水甚至流水的方式。

3) 受上部第三系红层影响,地下水水流呈铁锈

色,锈染严重。

2.3　水文地质条件

2.4　围岩力学参数

按不同岩性和风化、卸荷分带,根据地质调查、编录、平硐弹性波测试和钻孔取芯等大量统计成果,依据《水利水电工程地质勘察规范(GB50287—99)》和《工程岩体分级标准(GB50218—94)》的划分原则,综合确定各坝址岩体完整性及围岩力学参数。根据大量的裂隙调查统计、岩体钻孔压水试验成果和室内岩体试验,研究坝区岩石的强度特征及渗透特性,以及浅部风化带潜水和深部裂隙承压含水层,得到分区的力学参数及渗透系数见表1。根据提供的地质剖面图和洞室围岩类别可将整体围岩分为六类岩体,地下洞室几何模型见图1。

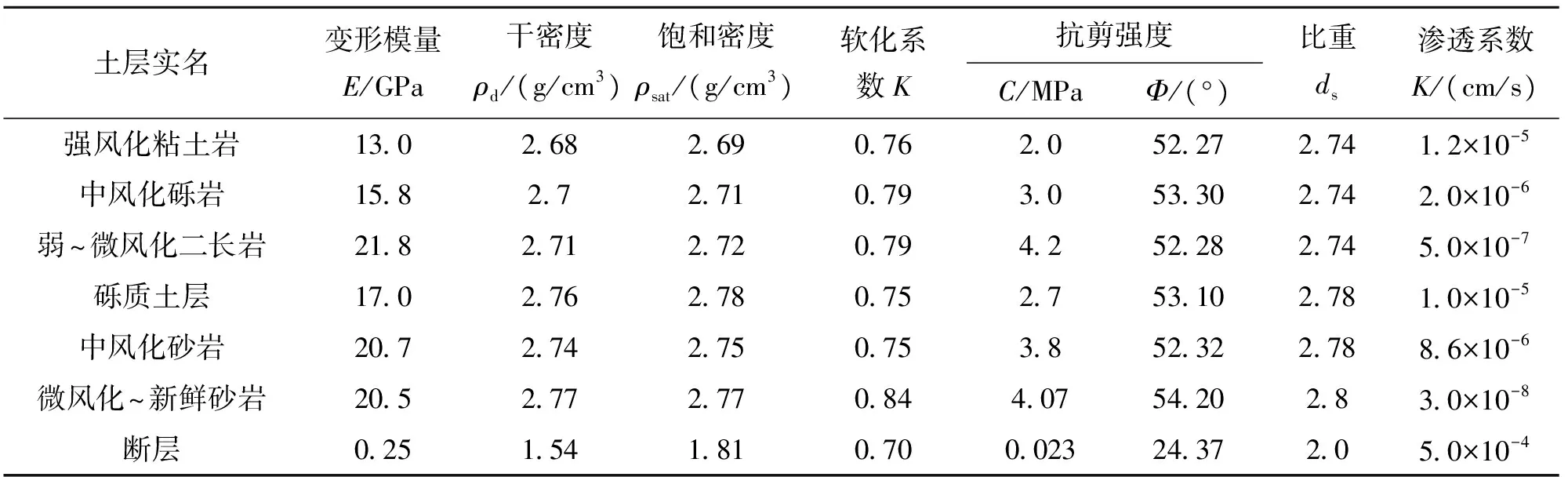
表1　围岩物理力学参数表[14]Tab.1　Physical and mechanical parameters of the surrounding rock

图1　地下洞室几何图Fig.1　The geometric figure of underground caverns

3　计算模型建立

3.1　模型建立

选取该地下厂房第Ⅲ剖面为分析断面,数值模型以垂直于厂房纵轴线方向并且指向下游为X轴正方向,铅直高度方向向上为正,是Y轴正方向。X方向的长度为376.6 m,Y方向从最低点起向上取到地表面,最大高度达约373.0 m[13]。根据地质剖面图和地质资料把计算区域剖分为三角形和四边形单元,单元总数为3 023个,单元结点总数为2 743个,洞室群二维有限元网格划分见图2。

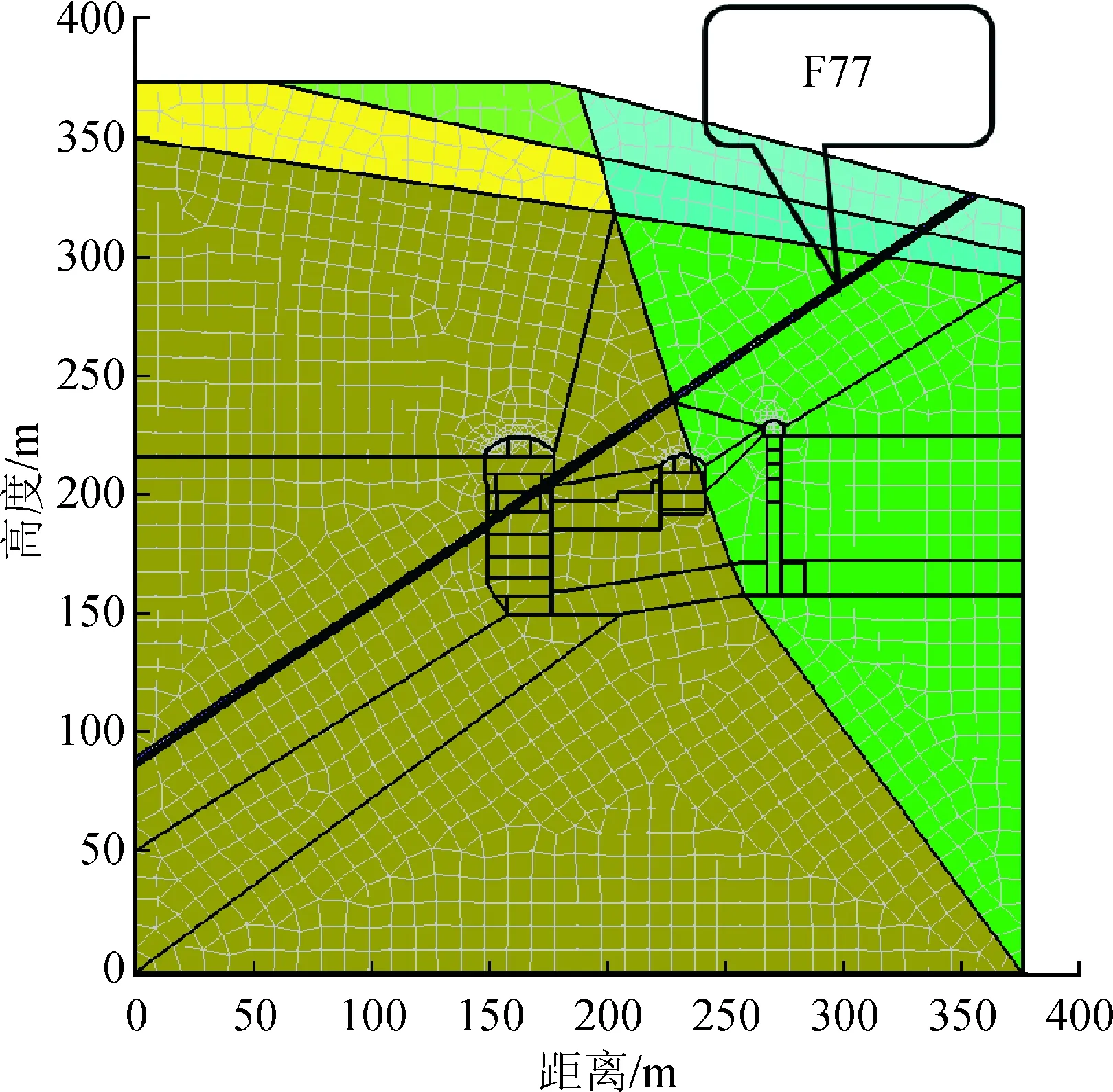
图2　计算区域网格剖分图(二维)Fig.2　Mesh generation of calculation region(2D)

3.2　边界条件选取及荷载

边界条件:底部边界为隔水边界,下游和上游为定水头边界(下游水头:376 m;上游水头:373 m)上部边界为降雨入渗边界,由于长期降雨,按照围岩处于饱和状态考虑,渗流按照稳态渗流计算。力学边界为模型上部，为自由表面,其底面和侧面均为水平和竖向约束,数值计算区域边界符合洞室围岩厚度大于5倍开挖跨度的条件。模拟区域包括主厂房、主变室、尾闸室、母线洞、引尾水洞等洞室。模型中考虑了岩性分界线、岩层分界线以及断层F77,断层与围岩呈侵入接触,接触面紧密,岩质无蚀变弱化迹象。

该水电站地下厂房竖直地应力以岩体自重应力为主,水平地应力采用竖直地应力乘侧压力系数K0以及构造运动产生的构造应力表示,如式(5)～(7)所示。地应力的施加方式采用体积力的赋值方法。

铅直主应力:

σV=γH

(5)

最大水平主应力:

σH=(K0+ε1)σV

(6)

最小水平主应力:

σH=(K0+ε2)σV

(7)

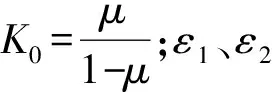
3.3　开挖方案模拟

地下洞室群设计开挖顺序见图3,本文模型开挖方案按照工程实际分为15步进行,洞室开挖方案见表2。

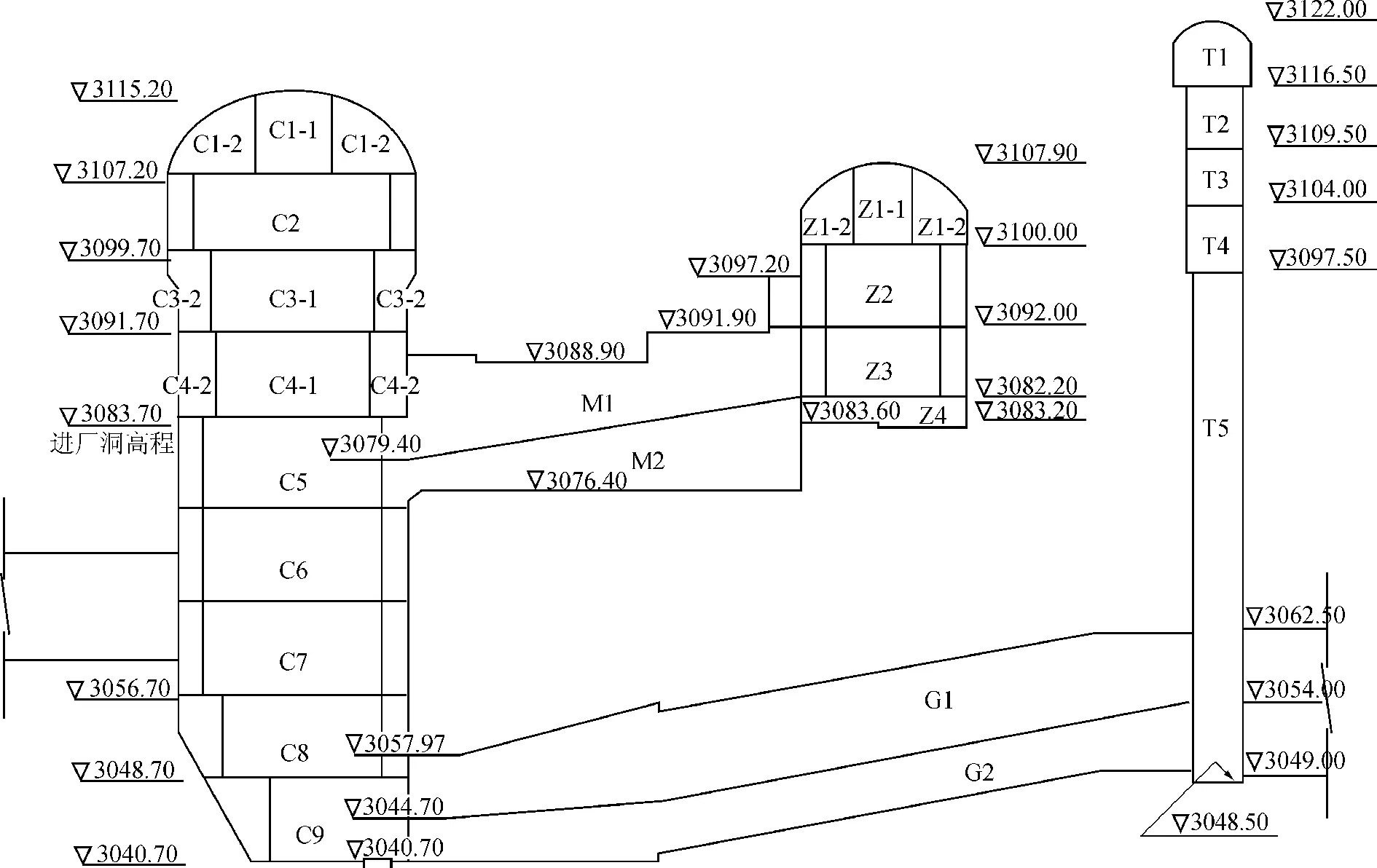
图3　厂房分层开挖示意图Fig.3　Excavation layers of powerhouse

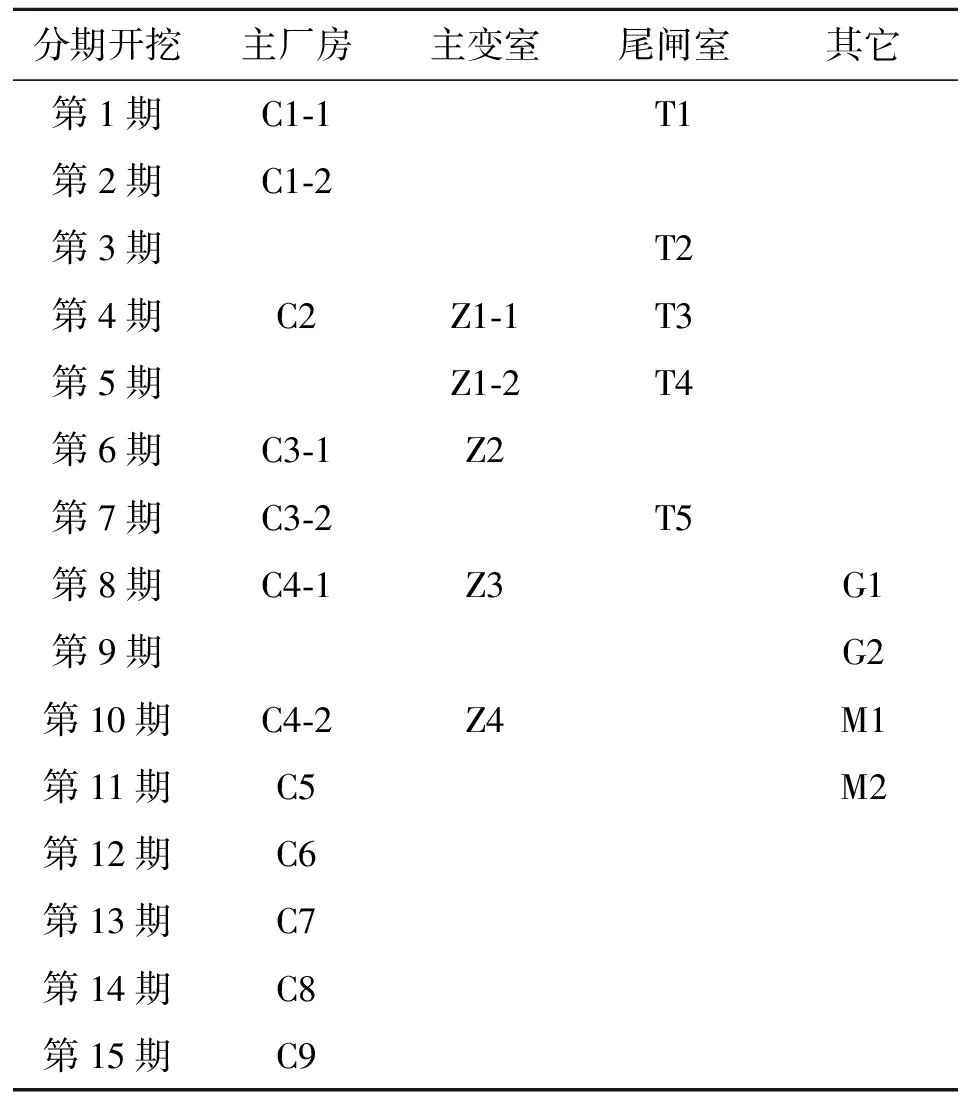
分期开挖主厂房主变室尾闸室其它第1期C1⁃1T1第2期C1⁃2第3期T2第4期C2Z1⁃1T3第5期Z1⁃2T4第6期C3⁃1Z2第7期C3⁃2T5第8期C4⁃1Z3G1第9期G2第10期C4⁃2Z4M1第11期C5M2第12期C6第13期C7第14期C8第15期C9

4　应力场对围岩稳定性的影响

4.1　计算工况

为了分析应力对地下厂房洞室群渗流场的影响以及对渗入厂房渗流量的影响,本文考虑如下两种计算工况进行对比分析:①工况1:仅考虑渗流作用;②工况2:考虑应力场和渗流场共同作用,即耦合作用。

4.2　计算结果分析

工况1和工况2的对比分析计算结果如下:

4.2.1渗流量结果分析

从通过岩体渗入地下厂房的渗流量来看,工况1和工况2最终向地下厂房的渗流总量分别为2 318.75 cm3/s和1 828.70 cm3/s,考虑耦合作用后,渗流量比原来减少了490.05 cm3/s。工况1和工况2各个洞室的渗流量的分布特征大体相同,不同洞室渗流量如表3所示。

表3　不同洞室渗流量Tab.3　Seepage flow of each chamber

从表3可以看出,主厂房的渗流量远大于其它洞室,依据地质勘察资料可知,最主要是由于有大断层F77穿过,主厂房受断层影响较大所致。工况1主厂房渗流量达到2 245.37 cm3/s,工况2主厂房渗流量达到1 770.80 cm3/s,其渗流量较大。因此,在施工程中,断层穿越处应及时做好防护排水措施。对于无断层穿过的主变室,尾水闸,母线洞和尾水闸渗流量变化不大,仅仅受过流断面积的影响,总体最大渗流量为55.21 cm3/s,对工程影响较小。与工况1相比,工况2各个洞室的渗流量有所减小,其原因在于厂房开挖过程中,考虑应力场的重新分布。应力场的改变导致体积应变发生变化,继而岩体中裂隙和断层会出现张开或闭合现象,渗透系数也会随之变化,截面面积含水量的减少受裂隙闭合的影响较大。岩石的渗透率会受应力状态的影响而表现出各向异性,因此,有效应力和裂隙的宽度关系很难准确把握。

4.2.2裂隙水压力结果分析

为验证应力作用对渗流场的影响,考虑了两种工况下的裂隙水压力,裂隙水压力的消散过程与应力过程相关,即渗流-应力耦合效应。根据计算结果,工况1和工况2的裂隙水压力等值线的分布有所不同,见图4。从图4可以看出,仅考虑渗流场时,裂隙水压力等势线的分布较为均匀,等势线沿Y轴正方向逐次减小。工况1中上游最大裂隙水压力为3.5 MPa,厂房底部裂隙水压力为0.5 MPa,厂房顶部裂隙水压力为-0.5 MPa。考虑应力场和渗流场共同作用时,裂隙渗透系数随法向应力的增加而降低,也可能随着侧向压力的增加而增大。对比图4中图(a)和图(b),地下厂房的裂隙水压力分布规律差别不大,但裂隙水压力值的大小有所变化,主厂房底部的裂隙水压力由0.5 MPa减小到0.2 MPa。工况2中下游最大裂隙水压力为3.2 MPa,厂房顶部裂隙水压力为-0.4 MPa。随着地下厂房的开挖,工程荷载和施工活动作用于岩体之上,岩体结构受到一定影响,应力场重分布致使渗透系数发生变化,从而引起裂隙水压力发生改变,在洞室周围可能产生新的裂缝,也可能使原有的裂缝发生闭合,最终引起岩体中地下水形态和力学特征的改变。

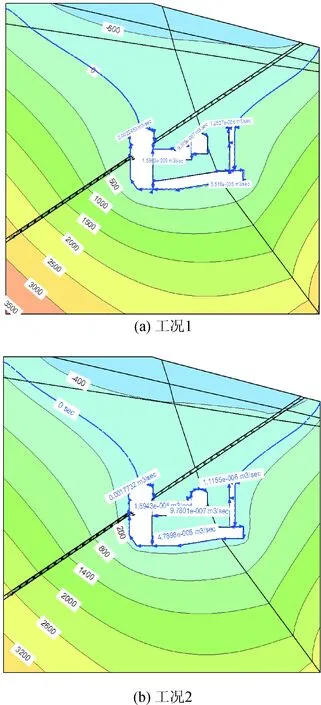
图4　裂隙水压力等值线图Fig.4　The pore-water pressure isoline

5　渗流场对围岩稳定性的影响

当岩体中存在渗流时,由于水流的力学、物理、化学等作用,会对岩体的抗剪强度有较大的影响。岩体处于干燥状态时,它的抗剪强度表示为:

τ=σtanφ+c

(8)

其中:τ为干燥状态岩体的抗剪强度,c和φ分别为干燥状态岩体的粘聚力和内摩擦角,σ为岩体滑动面的法向应力(即法向有效应力)。

岩体处于地下水位以下,并且出现随意方向的渗流时,岩体的抗剪强度表示为:

τ=σ′tanφ′+c′=(σ-γH+γJHsinα)tan(φ-

Δφ)+(c-Δc)±γJH|cosα|

(9)

其中:σ′为滑动面上的法向有效应力;c′,φ′分别为处于静水中的岩体的粘聚力和内摩擦角;Δc,Δφ分别为静水使岩体的粘聚力和内摩擦角的降低值;γ为水的容重;H为已知水头;α为水平方向到渗流方向的夹角;J为水头h沿渗流方向l的水力坡度[15]。

5.1　计算工况

为分析开挖过程中渗流对地下厂房洞室群应力场的影响,本文探讨以下两种工况且进行对比分析:①工况1:仅考虑应力场作用;②工况2:考虑渗流场作用,即渗流场与应力场产生耦合。

5.2　计算结果分析

5.2.1应力结果分析

厂房轴线方位NW320°时,地下厂房中心剖面应力场分布见图5～6(单位:MPa)。图中垂直坐标为厂房分析模型高程的起点向上取到地表面，水平坐标为厂房纵轴线方位NW320°的水平方向分析区域范围(单位：m)。

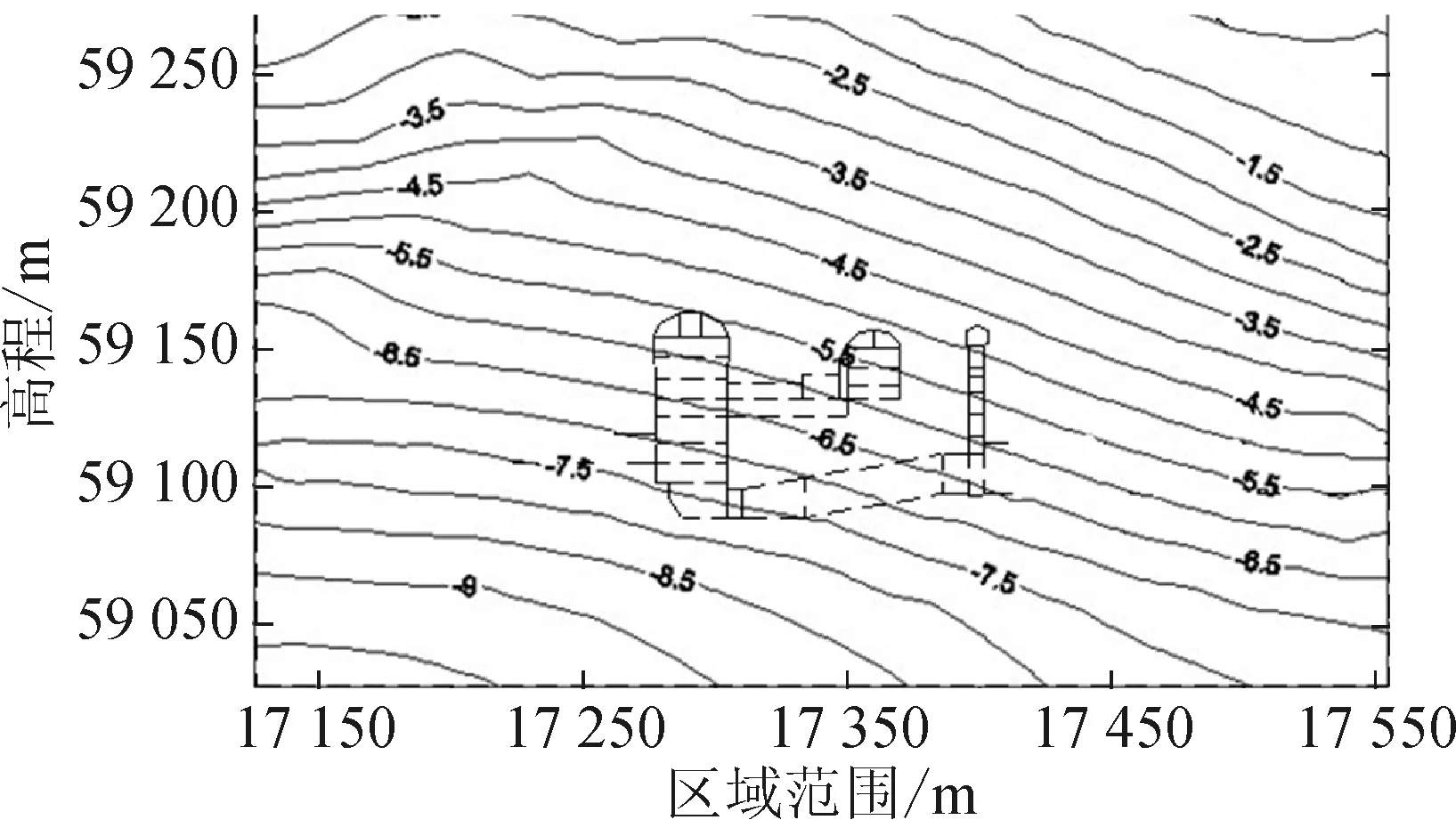
图5　厂房剖面水平方向应力分布图Fig.5　Stress distribution in horizontal direction of center section

图6　厂房剖面竖直方向应力分布图Fig.6　Stress distribution in the vertical direction of the center section

依据开挖方案,随着开挖的推进,开挖洞室周围的最大压应力和最大拉应力总体呈现慢慢增大趋势。第15步开挖完成后应力云图见图7。由图7可以看出:(工况1)厂房开挖完成后,洞周围岩应力分布均匀,第一主应力σ1多为切向应力,σ1逐渐增加,第三主应力σ3多为径向应力,向洞内释放,逐渐减小。随着施工过程的推进,下部开挖对围岩应力的扰动逐渐减小。在主厂房的两拱边断层部位、主厂房与主变室之间以及洞室拐角等部位出现明显的应力集中现象。主变室上游边墙和尾水闸的两边墙部位压力值较大,出现应力松弛区,这些相应部位在施工过程中应加强监控和支护处理,以防止应力释放产生的围岩破坏。开挖完成后厂区围岩主要以压应力为主,局部围岩有拉应力存在,最大压应力18.1 MPa,最大拉应力0.72 MPa。虽然存在拉应力,但量值不大。

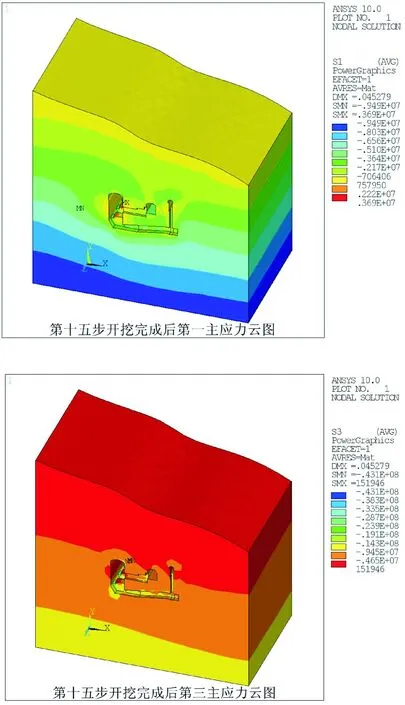
图7　第15步开挖完成后应力云图Fig.7　Stress contours after the completion of 15th step excavation

两种工况的洞周应力分布规律大体相同,工况2情况下,洞周径向和切向应力值略有增大,主厂房顶拱和断层部位、两侧边墙及洞室连接部位应力集中现象有所增加,主厂房边墙出现一定范围的拉应力。各洞室的拉应力和压应力都略有加大,但压力值增大幅度不大于2 MPa。由此说明地下水的渗流作用对洞周围岩的应力分布没有太大影响。水体在岩体中形成的渗流场不仅会降低围岩的抗剪强度,而且渗流场在岩体中形成的渗透力会成为外部荷载,增加围岩内部的剪应力。

5.2.2位移结果分析

图8(工况1)为第14步和15步开挖完成后总变形云图。洞室开挖完成后,三个洞室围岩的变形规律基本相同,均向洞室的临空面变形。主厂房上游边墙变形最大,主要以水平变形为主,最大变形32.6 mm,拱顶下沉,变形相对较小,底板出现回弹,在洞室交叉口处,位移梯度有所增大,分布不均匀。主变室受主厂房和母线洞开挖的干扰,拱顶及下游边墙变形较大,拱边相对较小,最大变形11.5 mm。尾闸室下游边墙变形最大,拱顶变形相对较小,最大变形18.2 mm。随着开挖的进行,上部围岩变形受下部岩体开挖的影响逐渐减弱,比较三大洞室的变形可以看出,主厂房的变形比尾水闸大,而主变室的变形相对较小。

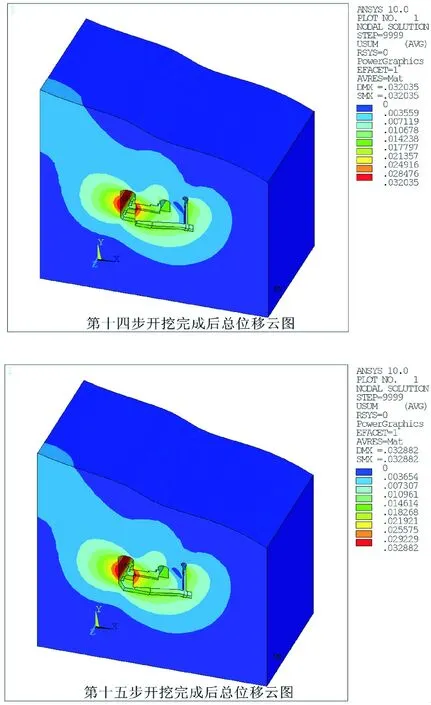
图8　第14-15步开挖完成后总变形云图Fig.8　Total deformation cloud after the completion of 14-15th step excavation

洞室周围关键点示意图,见图9。开挖过程中,围岩各关键点的变形变化规律见图10。

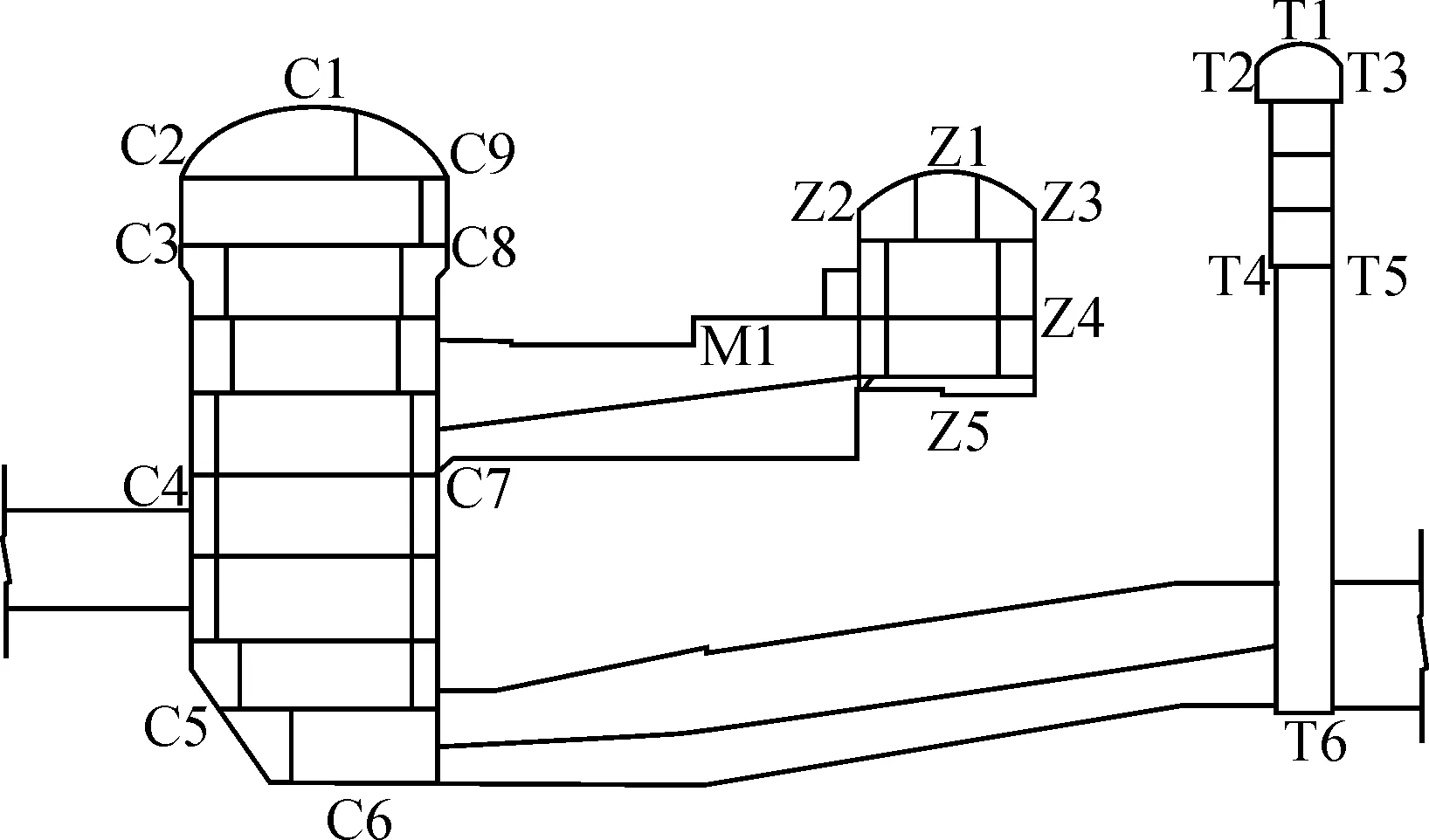
图9　洞室周围关键点示意图Fig.9　Schematic diagram of the key points around the cavern

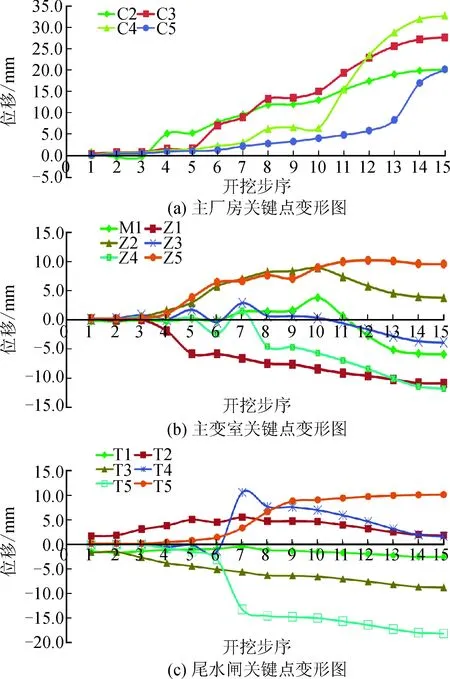
图10　各关键点变形规律图Fig.10　The deformation regularity of each key point

从图10可以看出,开挖完成后变形最大位置在主厂房上游边墙,其值为32.6 mm;下游边墙变形值为30.6 mm,主变室下游边墙变形值为11.9 mm,底板变形值为9.5 mm;尾闸室拱顶变形值为4.8 mm,上游边墙变形值为1.6 mm,下游变形值为18.2 mm,底板变形值为7.7 mm。洞室分层开挖对围岩的位移有很大的影响,各个关键点的位移量随施工的进行不断的增大。虽然位移量值均在允许范围内,但仍需对以各洞室的关键部位进行支护加固。

开挖完成后,工况2的洞周位移变化分布与无渗流工况规律类似,耦合作用下,主厂房上游边墙最大位移增加了8.4 mm,增大了25.7%;主变室下游边墙增大到14.7 mm,增大了18.5%;尾水闸下游边墙位移约增大了6.7 mm,各洞室的其它关键部位变形增加幅度相对较小。对比两种工况,渗流作用增加了围岩的变形且对围岩稳定性造成一定的威胁。

5.2.3塑性区结果分析

全部开挖完成后,塑性区主要分布在主厂房上游边墙、拱边和主厂房与主变室之间区域,分布的范围较广,深度较大,三个洞室拱顶塑性区分布较均匀,但深度不大。两种工况开挖完成后的塑性区分布图见图11。(工况1)主厂房上下游边墙最大塑性区范围分别约为9.8 m和7.6 m,断层穿越部位塑性区有所增大。主变室上下游边墙最大塑性区范围分别为5.4 m和5.3 m,底部最大塑性区范围约5.7 m。尾闸室塑性区分布范围较小,其拱顶最大塑性区范围约2.2 m。锚杆的锚固长度必须大于各洞室围岩破坏区的范围,且要打入完整岩体一定长度,以保证增强围岩稳定性的作用。

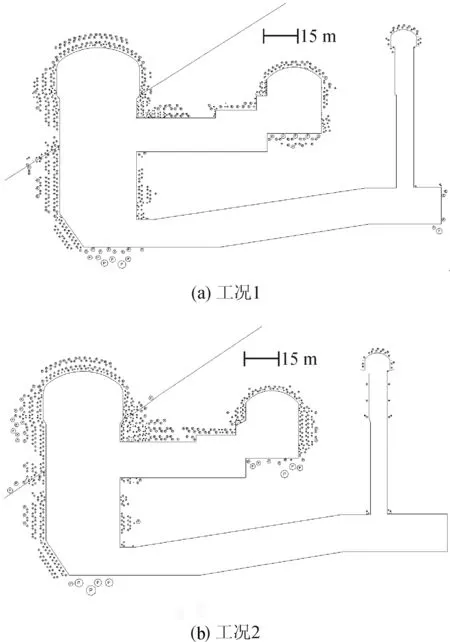
图11　开挖完成后塑性区分布图Fig.11　Plastic zone after the completion of excavation

从塑性区分布范围来看,考虑渗流作用后,塑性区范围比工况1明显增大,雨水和地下水致使岩体的扰动和破坏区范围增加。工况2情况下,主厂房上游边墙最大塑性区范围约11.52 m,下游与母线洞交接处最大塑性区范围约10.6 m,主变室下游边墙最大塑性区深度约6.4 m,比工况1的增幅达38%。由此可见,渗流场增加了洞室附近岩体的塑性区发展,对围岩的稳定性不利。

6　结　论

1) 由于该水电站地下厂房洞室群处于地应力较高、有大断层F77穿越主厂房、岩体类型复杂、工程环境恶劣等不利条件下,地下水和长期大量降雨使有断层穿越的洞室群发生变形、渗水和围岩松动区连续发展等现象。因此,本文采用流固耦合理论对该厂房进行稳定性分析且紧密关注其发展。

2) 持续降雨情况下,岩体长期处于饱和状态,且有大断层横穿主厂房,仅考虑渗流作用时,主厂房内的渗流量达到2 245.37 cm3/s。考虑耦合作用时,主厂房的渗流量为1 828.7 cm3/s。其他洞室的渗流量相对较小,最大不超过55.0 cm3/s。建议在断层穿越处做好支护和排水的有效措施。本文仅对渗流场采用了二维分析,并未做三维场的分析,在后续工作中将继续努力改进。

3) 厂房处于高应力区域,洞室开挖后主厂房上游边墙和主变室的下游边墙产生较大的压应力,最大压应力为18.1 MPa,洞室拐角处和洞室交汇处均出现应力集中现象。耦合作用下,各洞室的应力值增大幅度不超过2 MPa,应加强拉应力和应力集中部位的支护。

4) 开挖完成后,洞室的变形以水平位移为主,边墙位移大于拱顶和底板等其他部位,非耦合作用下,最大位移为32.6 mm,塑性区最大分布范围为9.8 m。耦合作用下,位移增大了25.7%,塑性区最大增长幅值为38%。

5) 渗流场作用使岩土体的抗剪强度降低,对地下厂房围岩稳定性影响较明显,考虑应力场和渗流场耦合作用是非常必要的。尤其是关键部位和应力集中部位应加强排水和锚固支护措施。

参考文献:

[1] 姚显春, 李宁, 陈莉静, 等. 拉西瓦水电站地下厂房洞室群分层开挖过程仿真反演分析 [J]. 岩石力学与工程学报, 2011, 30(增刊1): 3052-3059.

YAO Xianchun, LI Ning, CHEN Lijing, et al. Back analysis of surrounding rock stability based on excavation process underground powerhouse at LAXIWA Hydropower Station [J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(S1): 3052-3059.

[2] 石广斌, 李宁. 高地应力下大型地下硐室块体变形特征及其稳定性分析 [J]. 岩石力学与工程学报, 2009, 28(增刊1): 2884-2890.

SHI Guangbin, LI Ning. Analyses of block deformation characteristics of large underground cavern and its stability under high in-situ stress [J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(S1): 2884-2890.

[3] 李宁, 孙宏超, 姚显春, 等. 地下厂房母线洞环向裂缝成因分析及处理措施 [J]. 岩石力学与工程学报, 2008, 27(3): 439-446.

LI Ning, SUN Hongchao, YAO Xianchun, et al. Cause analysis of circumferential splits in surrounding rock of busbar tunnels in underground powerhouses and reinforced measures [J].Chinese Journal of Rock Mechanics and Engineering, 2008, 27(3): 439-446.

[4] 李宁, 罗俊忠, 常斌, 等. 硐室设计与分析的新思路与新方法 [J]. 岩石力学与工程学报, 2006, 25(10): 2155-2159.

LI Ning, LUO Junzhong, CHANG Bin, et al. New method for design and analysis of underground caverns [J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(10): 2155-2159.

[5] 苏国韶, 符兴义, 燕柳斌. 流场作用下大型地下厂房围岩稳定性分析 [J]. 地下空间与工程学报, 2010, 6(4): 717-723.

SU Guoshao, FU Xingyi, YAN Liubin. Surrounding rock stability analysis of large underground plant under seepage condition [J]. Chinese Journal of Underground Space and Engineering, 2010, 6(4): 717-723.

[6] 苏鹏云, 肖明. 瀑布沟水电站地下厂房岩体渗流场对围岩稳定的影响分析 [J]. 水电站设计, 2005, 21(2): 24-28.

SU Pengyun, XIAO Ming. Analysis of Pubugou Hydroelectric Power Station underground power house rock mass seepage field impacts on surrounding rock stability [J]. Design of Hydroelectric Power Station, 2005, 21(2): 24-28.

[7] 李宁, 张平, 段庆伟, 等. 裂隙岩体的细观动力损伤模型 [J]. 岩石力学与工程学报, 2002, 21(11): 1579-1584.

LI Ning, ZHANG Ping, DUAN Qingwei, et al. Dyanmic meso-damage model of jointed rock mass [J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21(11): 1579-1584.

[8] 柴军瑞. 大坝及其周围地质体中渗流场与应力场耦合分析 [D]. 西安: 西安理工大学, 2000.

CHAI Junrui. Analysis of coupled seepage and stress fields in dam and its surrounding rock mass [D]. Xi’an: Xi’an University of Technology, 2000.

[9] 裴桂红, 吴军, 刘建军, 等. 深基坑开挖过程中渗流-应力耦合数值模拟 [J]. 岩石力学与工程学报, 2004, 23(增刊2): 4975-4978.

PEI Guihong, WU Jun, LIU Jianjun, et al. Numerical modeling of seepage-stress coupling of deep foundation pit excavation [J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(S2): 4975-4978.

[10] 倪才胜, 白世伟, 韩昌瑞. 某水力枢纽基坑开挖过程渗流耦合数值模拟 [J]. 岩土力学, 2008, 29(增刊1): 37-41.

NI Caisheng, BAI Shiwe, HAN Changrui. Numerical simulation of hydro-mechanical coupling for a hydraulic project pit in excavation process [J]. Rock and Soil Mechanics, 2008, 29(S1): 37-41.

[11] 柳厚祥, 李宁, 廖雪, 等. 考虑应力场与渗流场耦合的尾矿坝非稳定渗流分析 [J]. 岩石力学与工程学报, 2004, 23(17): 2870-2875.

LIU Houxiang, LI Ning, LIAO Xue, et al. Unsteady seepage analysis of tailings dams considering coupling of stress and seepage fields [J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(17): 2870-2875.

[12] 侯伟. 公路隧道的渗流场与应力场的耦合分析 [D]. 西安: 西安理工大学, 2006.

HOU Wei. Analysis of coupled seepage fields and stress fields in highway tunnel [D]. Xi’an: Xi’an University of Technology, 2006.

[13] 赵靖伟. 青海玛尔挡水电站厂区地下洞室群围岩稳定分析 [D]. 西安: 西安理工大学, 2014.

ZHAO Jingwei. Stability analysis of surrounding rock for underground cavities of Qinghai Ma’erdang Hydropower Plant [D]. Xi’an: Xi’an University of Technology, 2014.

[14] 张顺. 玛尔挡电站地下厂房洞室工程地质研究 [D]. 兰州: 兰州大学, 2011.

ZHANG Shun. Engineering geological study on caverns of the underground powerhouse at Ma’erdang Hydropower Station [D]. Lanzhou: Lanzhou University, 2011.

[15] 柴军瑞, 崔中兴. 渗流对土体抗剪强度的影响 [J]. 岩土工程技术, 2001, 12(1): 8-10.

CHAI Junrui, CUI Zhongxing. Effect of seepage on soil shearing strength [J]. Geotechnical Engineering Technique, 2001, 12(1): 8-10.