基于粗糙集理论的武汉市农业土地利用数据分析及规划决策研究*

梁本哲，王占岐

(中国地质大学(武汉)土地资源管理系，湖北武汉 430074)

0 引言

长期以来，决策主要是依靠人的经验，随着科学技术的进步与发展，经验决策逐步被科学决策所取代[1]。过去30年我国各个领域积累了大量生产、科研数据，如何从这些海量的数据中发现潜在有用的知识一直是科技工作者关注和研究的课题。在土地利用领域，主要通过引入地理信息系统技术、计算机技术和数学模型方法来解决实际问题并提供决策支持。农业土地利用领域的数据繁多复杂，容易受时空差异、数据采集技术及设备精度和人为等因素影响，导致数据不可避免地存在一定的误差或不完整、不精确或具有噪音。文章从排除数据噪音干扰、提高决策支持的角度，引入具有知识发现功能的数据挖掘技术，以此强化对农业土地利用规划数据的定量分析研究，从而给农业土地利用规划提供更多的涉及数据问题的决策帮助。而在数据挖掘的各类方法中，粗糙集理论擅长从数据中发现异常，排除噪音干扰，而且该理论具有较强的客观性。

目前，粗糙集理论已经被证实在实践中是非常有用的，国际上基于粗糙集理论开发了许多学习或应用系统，并已取得了良好的收益。粗糙集理论作为一种数据分析处理理论，在机器学习、知识发现、数据挖掘、决策支持与分析、信息安全、物联网、云计算、生物信息处理等领域得到了广泛应用[2]。在土地利用和农业科学领域，国内不少学者也运用粗糙集开展了一些研究和应用，比如叶回春等[3]研究了粗糙集理论在土壤肥力评价指标权重确定的应用，结果表明粗糙集理论比特尔斐法确定出的各指标权重更为合理、准确； 欧阳浩等[4]运用粗糙集方法对广东省的粮食产量影响因素进行分析，通过知识发现，表明化肥用量、水库总容量以及人均经营耕地面积等对广东省粮食产量影响较为显著； 王丹丹[5]利用粗糙集理论对河南省粮食产量各类影响因素的重要程度进行计算，并以此对河南省粮食产量的变化趋势进行了预测。通过对文献的分析发现，粗糙集理论在广泛的应用实践中已经被学者们证明具有较好的应用价值，而且在规划决策上也能提供基于客观事实的辅助决策支持。同时，张政超[6]、王学恩[7]等学者通过研究发现，粗糙集理论还有一些理论上的问题需要进一步优化，比如在数据库中如何降低算法的执行效率，在数据缺失及不协调情况下有效实现属性值离散化以及寻找快速约简算法等粗糙集理论均是需要进一步研究的重点。

1 研究方法

粗糙集(Rough Set，RS)理论由波兰学者Z.Pawlak[8]于1982年提出，主要具有特点和优点：擅长处理和分析不精确、不一致、不完整等各种不完备信息； 能够分析隐藏在数据中的事实，并能从中揭示潜在的规律； 不需要任何先验知识的介入，对数据分析具有很强的客观性和真实性； 通过等价关系对事物进行分类来认知知识，并且可用数学方法来分析和处理。这些特性和功能比较适合用来处理土地利用规划方面的相关数据。

(1)建立信息系统。粗糙集理论研究的对象是信息系统(也可称为决策表或决策系统)，可用一个四元组[9]表示：S=。其中，U表示对象的有限集合，U={x1，x2，…，xn}；A表示属性的有限集合，A={A1，A2，…，An}；V是属性值组成的集合，V={V1，V2，…，Vn}，其中，Vi是属性Ai的值域；f是属性和对象的函数，f(xi，Ai)∈Vi。将信息系统S的属性集合A分为条件属性集合C与决策属性集合D两部分，即A=C∪D且C∩D=Φ。

(2)对属性进行约简。将信息系统S的任意属性子集B⊆A所对应的不分明关系IND(B)定义为：

IND(B)={(x，y)∈U2|∀a∈B[a(x)=a(y)]}

(1)

令属性集合B⊆A，对任意属性a∈B，如果有IND(B)=IND(B-{a})，那么称a是B中不必要的，否则就称a是B中必要的。如果属性集合B⊆A满足IND(B)=IND(A)，∀a∈B，IND(B)≠IND(B-{a})，那么，B就是A的一个约简。通过分明矩阵来计算属性集合A中属性约简的核，记为CORE(A)：

CORE(A)={a：存在分明矩阵的某一项cij，有cij={a}}，其中，

cij={a∈A|a(xi)≠a(yj)}

(2)

(3)可信度分析。粗糙集理论用粗糙隶属函数来描述某一对象属于某一概念的程度，称作规则可信度，定义为：

(3)

(4)生成决策规则。保留决策表中最优属性集合C′或最小约简a′，删除多余的属性列，并对属性列中相同项进行合并，最后将决策表的每一个对象转化为固定的规则形式，即得到最终的决策规则。

2 数据准备

为了实证研究及分析其粗糙集理论的应用价值，选取了2001～2014年湖北省武汉市土地利用方面的农业基础数据进行实例研究(表1)。

表1 武汉市农业土地利用基础数据

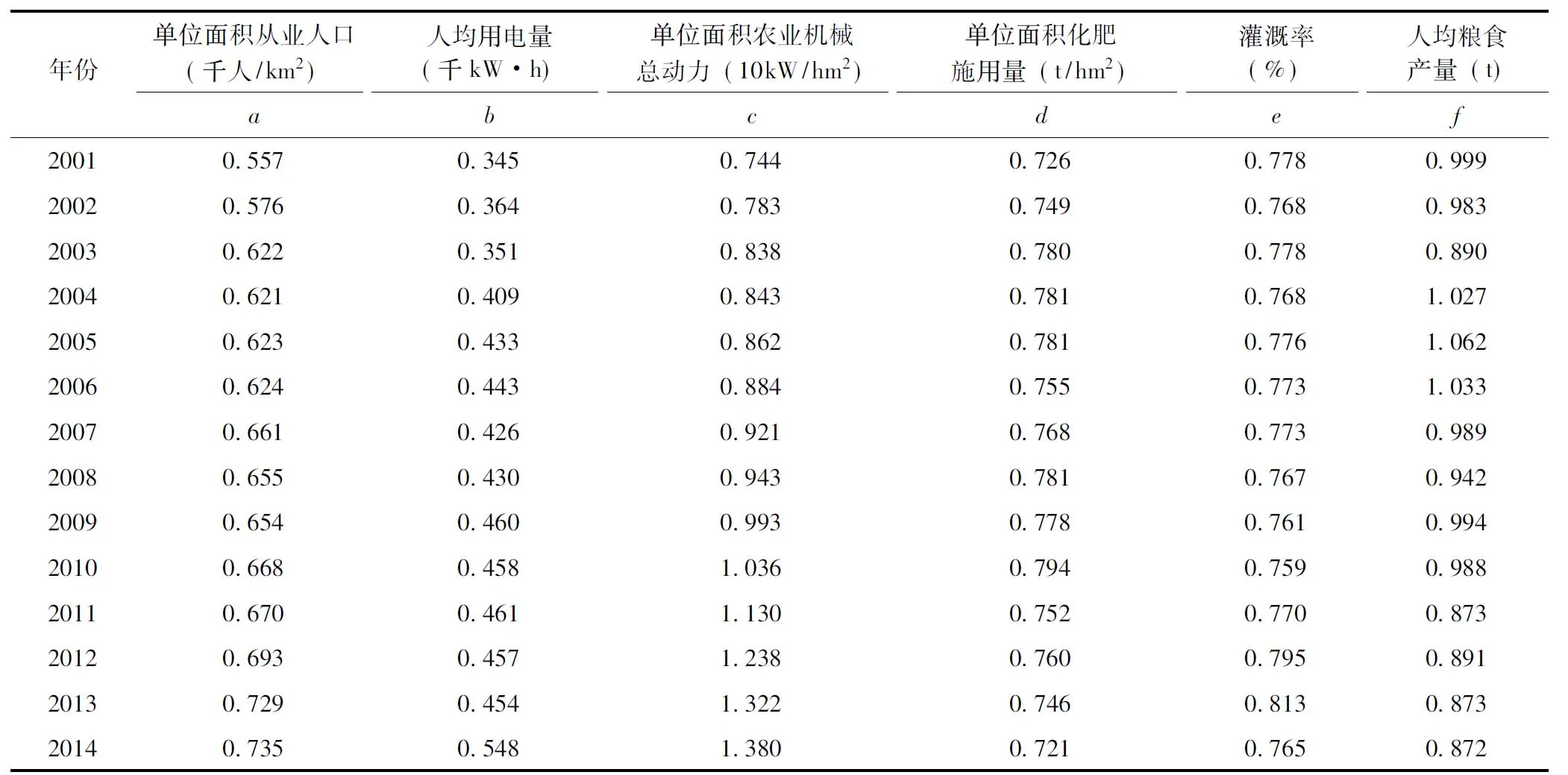
年份单位面积从业人口(千人/km2)人均用电量(千kW·h)单位面积农业机械总动力(10kW/hm2)单位面积化肥施用量(t/hm2)灌溉率(%)人均粮食产量(t)abcdef20010557034507440726077809992002057603640783074907680983200306220351083807800778089020040621040908430781076810272005062304330862078107761062200606240443088407550773103320070661042609210768077309892008065504300943078107670942200906540460099307780761099420100668045810360794075909882011067004611130075207700873201206930457123807600795089120130729045413220746081308732014073505481380072107650872 注：数据根据2002～2015年武汉市统计年鉴相关数据计算得到；单位面积从业人口=农村从业人口/耕地面积，人均用电量=农村用电量/农业人口，单位面积农业机械总动力=农业机械总动力/耕地面积，单位面积化肥施用量=农用化肥施用量/耕地面积，灌溉率=有效灌溉面积/耕地面积，人均粮食产量=粮食产量/农村从业人口

图1 2001～2014年武汉市农业土地利用基础数据变化趋势

3 粗糙集理论在具体决策问题中的应用

3.1 属性分类及离散化

从数据的变化趋势上看(图1)，属性d、e、f呈现不规律的变化趋势，而属性f的变化趋势更为复杂。根据粗糙集理论的属性分类规则，均可以将属性d、e、f设定为决策属性，但是考虑到属性f的变化趋势更为复杂，又对研究粮食安全问题具有更大的实际意义。因此，为了分析土地投入各项指标对人均粮食产量的影响，选择将a～e项土地投入类指标设为条件属性，将指标人均粮食产量f设为决策属性。

首先对以上数据表进行数据离散化处理，建立信息系统(即决策表，表2)。离散化过程即是利用选取断点来对条件属性的值域进行划分的过程，常用的离散化方法包括等距法、基于统计的方法、基于信息商的方法、基于遗传算法的方法等，通常，学者们采用模糊C均值聚类方法对条件属性进行离散化处理[10]。模糊C均值聚类方法进行分类时一般把相邻两类的边界属性值的算术平均值作为两分类的分界阈值。用分界阈值把连续属性的值域分为两个子区间，分别形成连续属性的两个离散值，标以不同的符号。如表2。

通过阈值划分，所有数据被分为两类，并用区间值表示。对决策属性进行分类，如人均粮食产量通过模糊C均值聚类方法的离散化处理，计算得到两分类的分界阈值为0.937，对其人均粮食产量高低水平进行定性描述，即可用分界阈值作为划分高低产量水平的标准。设定“>0.937”为高产(用H表示)，“≤0.937”为低产(用L表示)； 对所有条件属性进一步简化处理，得到简化决策表3。

表2 阈值划分后的决策

Uabcdef2001≤0640≤0429≤0990≤0761≤07800>09372002≤0640≤0429≤0990≤0761≤07800>09372003≤0640≤0429≤0990>0761≤07800≤09372004≤0640≤0429≤0990>0761≤07800>09372005≤0640>4292≤0990>0761≤07800>09372006≤0640>4292≤0990≤0761≤07800>09372007>0640≤0429≤0990>0761≤07800>09372008>0640>0429≤0990>0761≤07800>09372009>0640>0429>0990>0761≤07800>09372010>0640>0429>0990>0761≤07800>09372011>0640>0429>0990≤0761≤07800≤09372012>0640>0429>0990≤0761>07800≤09372013>0640>0429>0990≤0761>07800≤09372014>0640>0429>0990≤0761≤07800≤0937

表3 简化处理后的决策

3.2 属性约简及重要性检验

将决策表3表示成信息系统S=，令C={a，b，c，d，e}，D={f}，并对属性进行约简。该信息系统的等价类为：U/C={{x1，x2}，{x3，x4}，{x5}，{x6}，{x7}，{x8}，{x9，x10}，{x11，x14}，{x12，x13}}，U/D={{x1，x2，x4，x5，x6，x7，x8，x9，x10}，{x3，x11，x12，x13，x14}}。

C的D正域为：POSC(D)=∪{C(X)：X∈U/D}={x1，x2，x5，x6，x7，x8，x9，x10，x11，x12，x13，x14}，同理其他各正域为：POSC-{a}(D)=POSC-{c}(D)=POSC-{e}(D)={x1，x2，x5，x6，x7，x8，x9，x10，x11，x12，x13，x14}，POSC-{b}(D)={x1，x2，x6，x7，x8，x9，x10，x11，x12，x13，x14}，POSC-{d}(D)={x5，x6，x7，x8，x12，x13}。

由于POSC-{b}(D)≠POSC(D)，POSC-{d}(D)≠POSC(D)。所以b，d是D必要的，并且C相对于D约简的核为CORED(C)={b，d}。以相对约简的核{b，d}为起点，可以计算出所有的C相对于D的属性约简，POS{a，b，d}(D)={x1，x2，x5，x6，x7，x8，x9，x10，x11，x12，x13，x14}，POS{b，c，d}(D)= {x1，x2，x5，x6，x8，x9，x10，x11，x12，x13，x14}，POS{b，d，e}(D)= {x1，x2，x5，x8，x9，x10，x12，x13}。

由于POS{a，b，d}(D)=POSC(D)，由此可以得到决策表的重要属性集为{b，d}，最优约简属性集为{a，b，d}。根据以上约简属性，即可得到约简后的决策表，见表4。

表4 属性约简后的决策

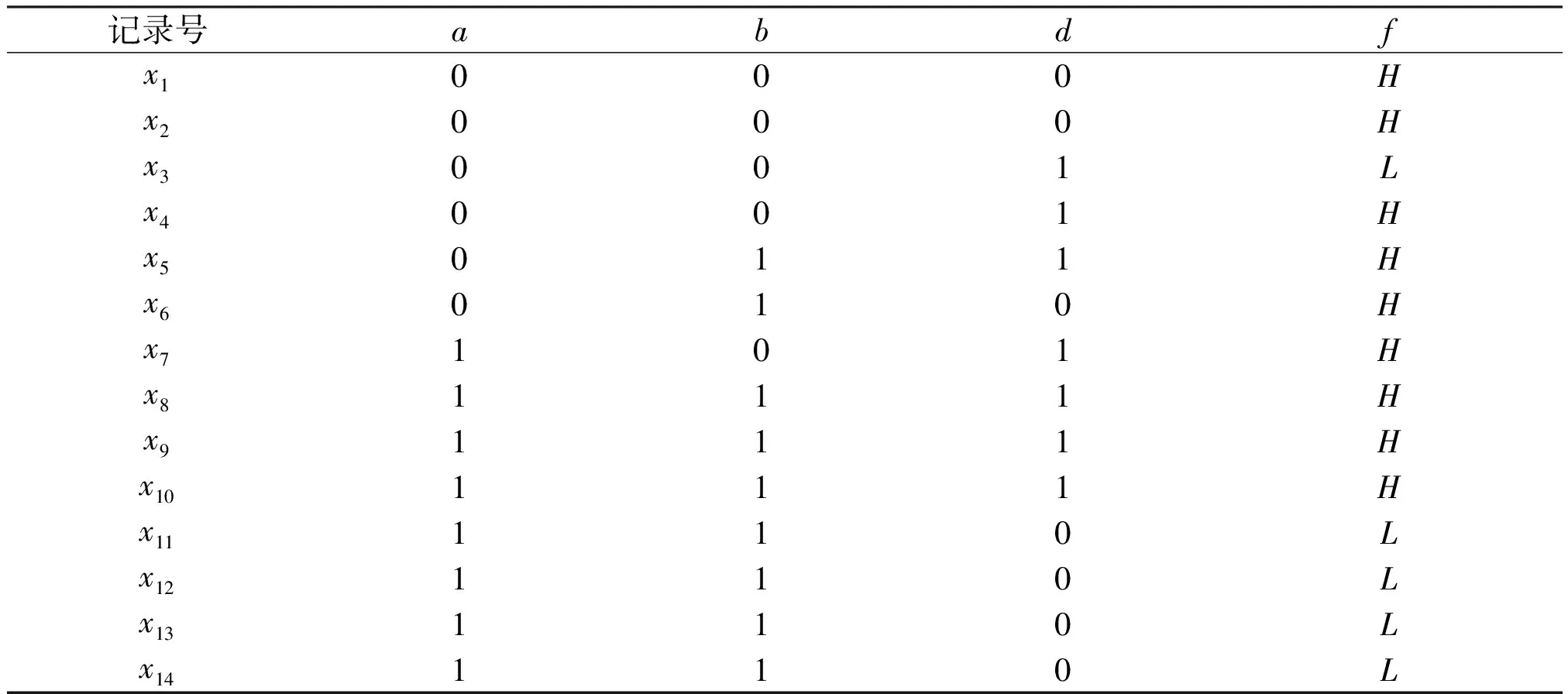
记录号abdfx1000Hx2000Hx3001Lx4001Hx5011Hx6010Hx7101Hx8111Hx9111Hx10111Hx11110Lx12110Lx13110Lx14110L

3.3 提取决策规则

为了更好地反映各条件属性对决策属性的定量化影响关系，通过提取决策规则来体现。根据粗糙集理论决策规则的形成方法，最终得到决策表的决策规则，从规则表(表5)可以看出，规则2与规则3在同样条件下出现了不一致的结果。因此，对于决策者而言，在利用规则之前，必须了解规则的可信程度，以便更科学、合理地辅助决策。

表5 决策规则

规则编号记录号规则描述结果可信度综合可信度1x1，x2a≤0640∧b≤0429∧d≤0761H1000142x3a≤0640∧b≤0429∧d>0761L0500043x4a≤0640∧b≤0429∧d>0761H0500044x5a≤0640∧b>0429∧d>0761H1000075x6a≤0640∧b>0429∧d≤0761H1000076x7a>0640∧b≤0429∧d>0761H1000077x8，x9，x10a>0640∧b>0429∧d>0761H1000218x11，x12，x13，x14a>0640∧b>0429∧d≤0761L100029 注：某项规则的综合可信度=(可信度×记录数)/总记录数，以规则1为例，其综合可信度=100×2/14=014

3.4 规则解释

根据分析，可以得出结论。

(1)决策规则集给出了8条确定性规则，可将其转化为语言进行描述，以规则7、8为例，得到的武汉市人均粮食产量水平变化的定量化表达为：当某一年武汉市单位面积从业人口大于640人，人均用电量大于429 kW·h，单位面积化肥施用量大于0.761t/hm2时，则当年的人均粮食产量将高于0.937t，属于高产水平； 当某一年武汉市单位面积从业人口大于640人，人均用电量大于429 kW·h，单位面积化肥施用量小于0.761t/hm2时，则当年的人均粮食产量将低于0.937t，属于低产水平。

(2)规则7、8的综合可信度最高，可将其分别作为人均粮食产量高、低产水平的代表性规则。从图1显示的基础数据的变化上看，单位面积从业人口(a)和人均用电量(b)均呈逐年上升趋势，结合规则7、8的表达式可以得出，若进一步研究武汉市人均粮食产量的变化趋势，单位面积化肥施用量(d)将是唯一的影响因素，当单位面积化肥施用量小于0.761t/hm2时，人均粮食产量处于低产水平，大于0.761 t/hm2时，人均粮食产量将处于高产水平。

(3)从规则分析来看，武汉市的人均粮食产量变化与单位面积从业人口(a)、人均用电量(b)和单位面积化肥施用量(d)等3者有密切的联系，且单位面积化肥施用量的影响最为显著。欧阳浩[4]、王丹丹[5]等对广东省粮食产量影响因素分析中，也验证了化肥用量对粮食产量有着显著影响。王奇等[11]基于粮食产量与化肥施用的定量关系对我国粮食安全与水环境安全之间的关系进行了分析，结果表明，化肥施用量不仅关系着粮食安全，同时也对水环境产生一定影响，对水环境安全构成一定威胁。

3.5 武汉市粮食产量趋势预测及分析

运用前文分析的结论，可以对武汉市未来人均粮食产量情况进行预测分析。粗糙集理论最大的优点就是挖掘出来的规则具有较强的客观性，为了使预测结果也更具有客观性，这里不直接对单位面积化肥施用量按照其变化规律进行预测，而是分别对耕地面积和化肥施用量的变化趋势预测后再计算出单位面积化肥施用量的变化情况。因此，通过建立线性回归模型进行计算，得到未来10年两者的预测值，再结合预测值计算出单位面积化肥施用量(表6)。对照决策规则7、8，如果按照目前武汉市耕地粮食生产的投入条件趋势发展，可推断出今后10年武汉市人均粮食产量的水平将一直处于小于0.937t的低产水平。

表6 2015～2024年武汉市人均粮食产量水平趋势预测

属性2015201620172018201920202021202220232024耕地面积(万hm2)19960198341970819582194561933019204190781895218826化肥施用量(万t)14180138421350413166128281249012152118141147611138单位面积化肥施用量(t/hm2)0710069806850672065906460633061906060592人均粮食产量水平预测(t)≤0937≤0937≤0937≤0937≤0937≤0937≤0937≤0937≤0937≤0937

4 结论及展望

(1)未来10年武汉市人均粮食产量可能将一直处于低于0.937t的水平。武汉市农村从业人口近年来总体上呈逐年增加趋势，年均变化率为1.51%，而粮食总产量虽呈现不规律的变化，总体仍呈上升趋势，年均变化率为0.63%，但远低于农村从业人口的变化率，如果当前的趋势不发生异常变化，未来10年武汉市人均粮食产量将一直处于低产水平。随着新型城镇化的不断推进，大量的农业人口开始向非农化和城镇转移，未来农村从业人口结构势必会发生变化，人均粮食产量的水平也将会发生反转。同时，不断提高农业生产力水平以提高粮食产量，也将是提升人均粮食产量的重要途径。

(2)应重点加强对化肥施用量与粮食产量的定量化研究。随着农业生产力水平的不断提高，粮食单产水平不断提升，公众对于中国粮食安全的关注度在下降，但对于中国这样一个近14亿人口的超级大国来说，粮食安全问题将是恒久不变需要持续加强研究的课题。结合该文的分析结论，在研究武汉市粮食产量的变化趋势时，应重点考虑单位面积化肥施用量对粮食产量的影响。而且在当前推进生态文明建设过程中，还应注意分析区域粮食安全与其水环境安全之间的关系。

(3)将粗糙集理论嵌入GIS系统中，提升数据分析与决策能力，应成为未来研究的一个重要方向。由于采集的数据量有限，分析的结论可能存在一定的误差，但是分析得出的结论应该具有一定的参考借鉴价值，特别是挖掘的规则对于武汉市人均粮食产量水平的变化规律给予了定量化的描述，对于武汉市农业生产以及土地利用等方面能够提供一定的决策支持。当前，国内关于粗糙集理论的相关研究大多为方法的实证研究阶段。该文认为，如何将粗糙集理论及方法嵌入到GIS系统中，充分运用其数据挖掘功能，从海量数据中提取隐含的客观规律，有效提升系统的数据分析和科学决策能力，将是今后研究的重点。

[1] 唐华俊. 专家系统和决策支持系统的异同及其应用.中国农业资源与区划， 1995, 16(3): 56～60

[2] 于洪， 王国胤，姚一豫.决策粗糙集理论研究现状与展望.计算机学报， 2015, 38(8): 1628～1639

[3] 叶回春， 张世文，黄元仿，等.粗糙集理论在土壤肥力评价指标权重确定中的应用.中国农业科学， 2014, 47(4): 710～717

[4] 欧阳浩， 戎陆庆，黄镇谨，等.基于粗糙集方法的广东省粮食产量影响因素分析.中国农业资源与区划， 2014, 35(6): 100～107

[5] 王丹丹. 基于粗糙集理论的河南省粮食产量预测研究.河南农业大学学报, 2015，49(6)： 876～880

[6] 张政超， 关欣，何友，等.粗糙集理论研究的新进展.计算机与现代化， 2009，(11)： 16-21+25

[7] 王学恩， 韩崇昭，韩德强，等.粗糙集研究综述.控制工程， 2013, 20(1): 1～8

[8] Pawlak Z.Rough Set.International Journal of Computer and Information Sciences， 1982， 11： 341～356

[9] 王国胤.Rough集理论与知识获取.西安：西安交通大学出版社， 2001

[10]孙英娟. 基于粗糙集的分类方法研究.长春：吉林大学， 2011

[11]王奇， 詹贤达，王会.我国粮食安全与水环境安全之间的关系初探——基于粮食产量与化肥施用的定量关系.中国农业资源与区划， 2013, 34(1): 81～86