大型风力发电机组塔顶法兰应力集中因数的有限元分析
□赵云琨 □李佳威 □刘恒山 □许梦华 □潘文豪
上海电气风电集团有限公司 上海 200030
1 研究背景
随着风力发电行业各项相关技术的快速发展,风力发电机组的功率越来越大。在兆瓦级大型风力发电机组中,塔架是重要的承载部件。塔架除了要支撑风力发电机组的重力,还要承受吹向风力发电机组和塔架的风压,以及风力发电机组运行中的动载荷,其设计水平将直接影响风力发电机组的性能[1]。塔顶法兰是连接塔架和前机架的关键部件,也是风力发电机组运行时塔架的主要受力部件,与偏航刹车盘、偏航轴承通过螺栓连接。在风力发电机组工作时,作用于叶轮和机舱的载荷通过偏航轴承传递到塔架上,因此塔顶法兰连接的可靠性和安全性对整个风力发电机组的正常运行而言有重要影响。
法兰连接系统所承受的是复杂多变的动载荷,在这些载荷作用下,系统各个部件可能发生屈服或疲劳损坏[2]。风力发电机组运行过程中,风轮旋转带来升力、阻力、轴向推力、气动弯矩和气动转矩等气动载荷,加之轮毂的不间断无规律震荡、微旋转等运动载荷,通过偏航轴承传递到塔架法兰和螺栓上[3]。塔筒间焊缝处和法兰圆角过渡处是结构中比较薄弱的环节,塔顶法兰由于长期承受动态载荷,易发生疲劳损坏。如果能在设计初期对焊缝和圆角的疲劳寿命进行预测,就可以对焊缝处理方式和圆角尺寸进行合理调整,进而提高产品的整体抗疲劳性能[4-5]。为了测算焊缝处和法兰圆角过渡处应力集中对法兰疲劳损坏的影响,在疲劳计算时引入应力集中因数用以放大时序载荷。根据应力集中对疲劳损坏的影响,针对焊缝处和圆角处进行必要的修整,以降低应力集中因数,进而减小法兰疲劳损坏。可见,为提高塔顶法兰使用寿命,进而提升风力发电机组运行的可靠性,对塔顶法兰应力集中因数进行计算是非常必要的。
应力集中往往受法兰受力状态影响,为具体分析法兰应力集中现象,首先进行法兰连接状态的受力和变形分析。笔者采用有限元仿真技术,结合相关理论对塔筒顶部法兰应力集中因数进行分析。有限元仿真采取整体建模和子模型共同分析的方法,分别计算塔顶法兰焊缝及过渡圆角等危险处的应力集中因数,在实际应用中利用该因数对塔顶法兰疲劳强度加以校核,同时采取减小应力集中因数的方法进行法兰加固。
2 法兰受力理论分析
风力发电机组通过法兰实现两塔筒节间,以及塔顶塔筒与偏航轴承、前机架等之间的连接。塔架在弯矩作用下发生振动,常见的振动方式为筒体左右摆动。
筒体摆动使连接法兰发生交替拉压变形,不但使法兰产生应力集中现象,而且造成法兰间交替出现缝隙或挤压变形。变形产生的法兰间隙不仅对螺栓的疲劳寿命造成不利影响,而且会增大法兰的疲劳损坏,严重影响法兰连接系统的结构强度[6]。
为了直观地进行塔顶连接法兰受力和变形分析,将偏航轴承和前机架等简化为一块整体法兰,与塔顶法兰经高强度螺栓连接形成法兰连接系统,其受力和变形理论同两塔筒节间理论相同。根据机械受力原理,分析法兰在弯矩作用下发生的变形。不考虑法兰连接后自存间隙及螺母端面与法兰间摩擦,结合图1和图2分析法兰受力及变形[7]。
风机处于不工作状态时,法兰仅受预紧力作用,发生如图2(a)所示挤压变形。预紧力指向螺栓外部,两法兰受挤压产生反作用力F0,单一法兰在连接部位分别受预紧力FF和F0,此时残余预紧力FCF=F0,连接部分因挤压而在两侧产生间隙。
加载弯矩后,整体法兰发生倾覆变形,体现在法兰连接处为拉伸或压缩变形。如图2(b)所示,在弯矩作用下,螺栓承受向上工作拉力F,总拉力为FCF+F。法兰承受的压缩力为残余应力F1,且持续压缩,同时,法兰经受向内倾覆的弯矩,因此外侧间隙加大,内测间隙减小。最终法兰和螺栓受力达到平衡,法兰总力F1=FCF+F。如图2(c)所示,螺栓在压力Fm作用下产生压缩,而法兰在F1m作用下释放原始间隙,同时在倾覆力矩作用下法兰内侧产生间隙。最终螺栓与法兰受力平衡,法兰总力F2m=F1m-Fm。对比法兰拉压两侧总力可见,F1>F2m,即受拉侧法兰受力大于受压侧,受拉侧更易发生应力集中。
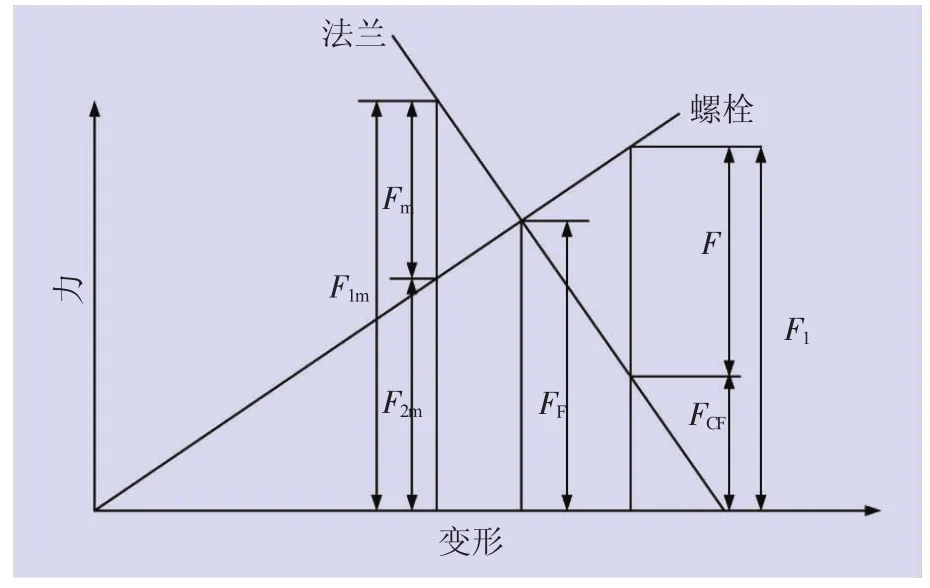
图1 法兰螺栓受力变形示意图
风力发电机组运行过程中,法兰因承受动载荷发生断续拉压变形,法兰拉压两侧受力状态不同,其应力分布亦不同,即应力集中会发生变化,因而损坏部位及程度也会不同。由于法兰应力集中易发生在圆角过渡处及与筒壁焊接的焊缝处,因此需要建立包含过渡圆角和焊缝的子模型,并加载总体模型位移在子模型上,分析子模型在不同拉压状态下圆角过渡处及与筒壁焊接焊缝处的应力分布,同时获得应力集中因数。
3 有限元结构分析
3.1 法兰有限元建模
仿真计算过程分为整体模型仿真计算和子模型仿真计算。塔顶整体有限元模型包括前机架假体、偏航轴承、刹车盘、塔顶法兰、部分塔筒及相应的连接螺栓等,如图3(a)所示。不同的部件材料,其特性不同,建模时需考虑的参数也不相同,表1给出了不同部件的材料参数,各接触面间摩擦因数取0.15[8]。子模型以较小的区域包含法兰的圆角和焊缝,在圆角处采用六面体加密网格,焊缝采用一圈节点模拟,与节点相关的单元采用较小网格,如图3(b)所示。应用子模型可以在研究塔顶法兰应力集中时获得足够精确的应力分布。
3.2 边界条件和加载
根据实际装配和受力情况,对模型边界进行约束。将塔架下端通过质量点单元统一约束6个自由度,以消除接触分析时的刚体位移[9]。为了反映真实受力状态,在塔顶法兰偏航刹车盘中心点处加载极限组合弯矩,并将极限载荷分10个子步逐一加载至模型。考虑到存在法兰连接螺栓预紧力,将加载载荷的第一子步设置为加载预紧力,从第二子步开始加载极限载荷分量。根据极限工况设置最大组合弯矩为8 764.520 kN·m。整体模型中螺栓均布于塔顶法兰,单一螺栓预紧力F0为510.00 kN,预紧因数γo为1.2,预紧力损失F1为9.00 kN。

表1 材料物理力学性能
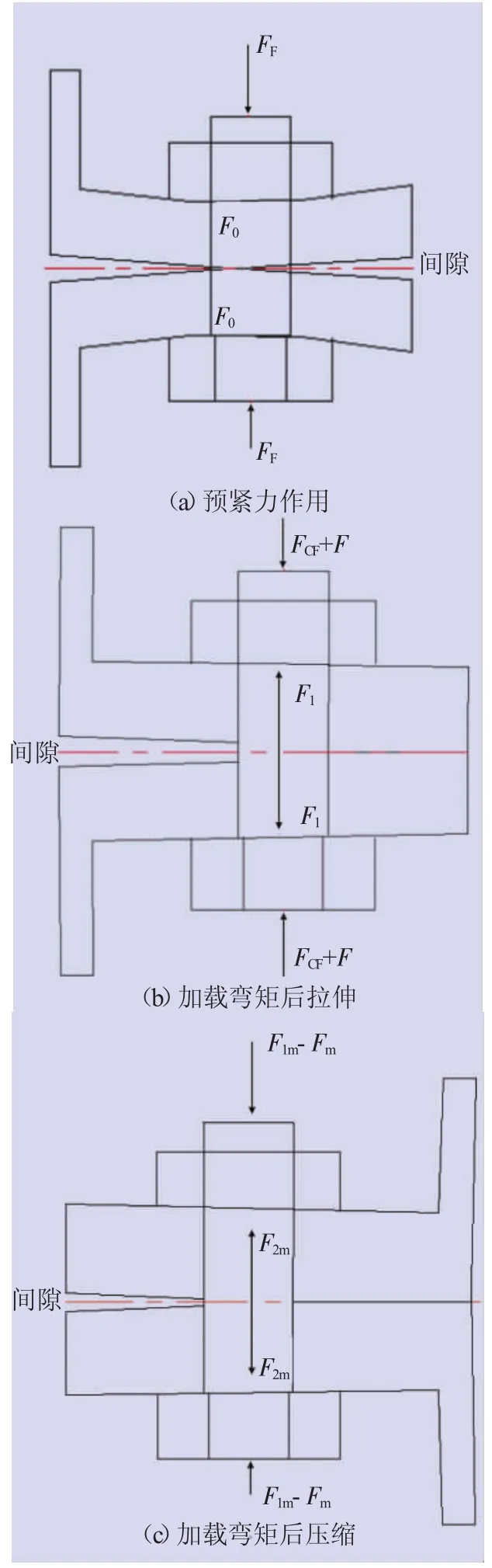
图2 法兰受力变形示意图

图3 塔顶有限元模型
根据公式F=F0/γo-F1[10],计算单一螺栓实际预紧力F为416 kN。塔顶共有72个螺栓,这样单个预紧单元上加载的力为29 952 kN。
3.3 整体模型有限元分析
在轴心处加载垂直于YOZ平面的顺时针弯矩,得出塔顶整体模型位移图和塔顶法兰位移图,分别如图4、图5所示。由图4可知,塔顶沿着弯矩方向受到压应力而发生挤压,反方向则发生拉伸,最大位移为0.002 907 m。塔顶法兰与偏航刹车盘、偏航轴承等连接等效于与法兰连接,单独分析法兰应力状态,由图5可知,法兰最大位移出现在塔筒两侧,最大变形量为0.001 091 m。法兰变形小于塔顶最大变形量,主要是由于法兰和塔顶之间有前机架体缓冲顶部力的作用。

图4 塔顶整体模型位移图
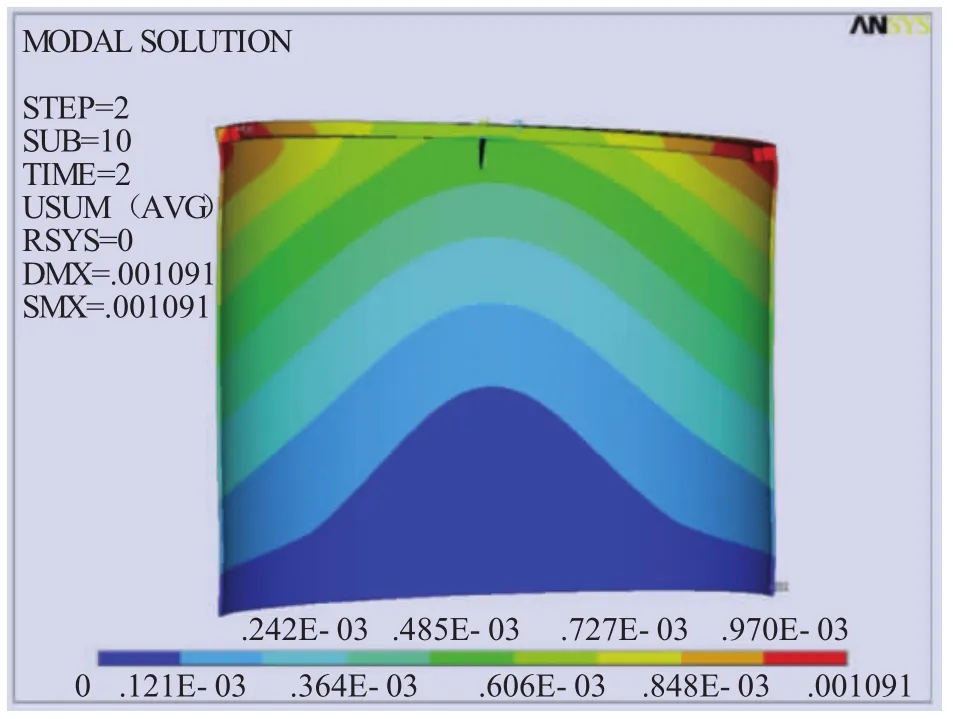
图5 塔顶法兰位移图
由于变形由应力集中引起,因此结合位移分析塔顶法兰受力情况。图6为塔顶应力分布情况,塔顶在弯矩作用下最大应力为900 MPa,发生在塔筒轴向左侧,右侧应力集中最大值约为400 MPa,与轴向两侧成90°位置几乎不受力。在应力作用下,法兰发生拉伸和压缩,为进一步确定法兰状态,进行法兰第一主应力分析。由图7可知,塔顶右侧受压应力,最大为-55.1 MPa;左侧受拉应力,最大为173 MPa。由此可见,塔顶受拉侧应力集中大于受压侧,受拉侧变形大于受压侧,即受拉侧较危险。
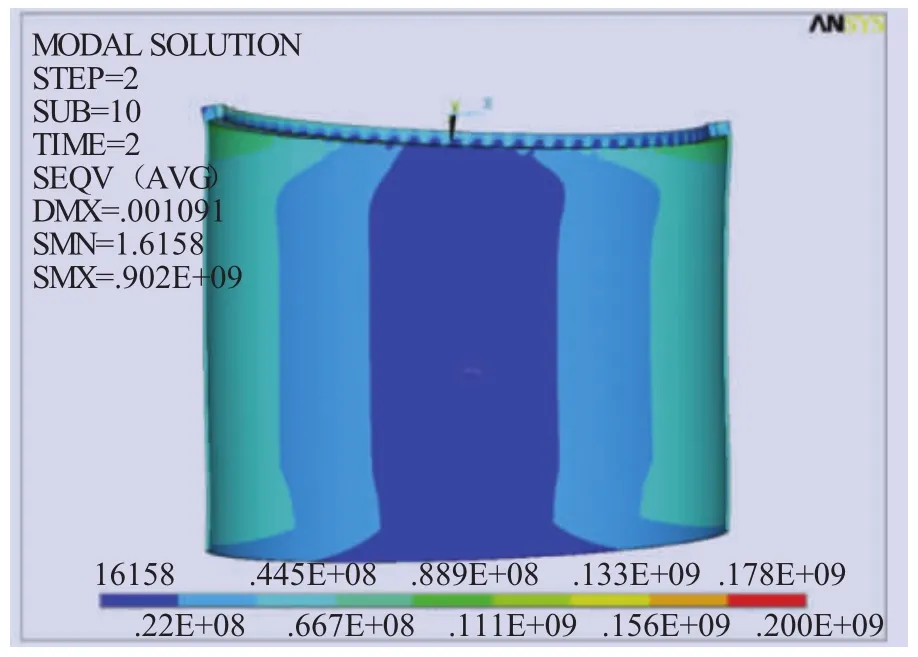
图6 塔顶整体模型应力图
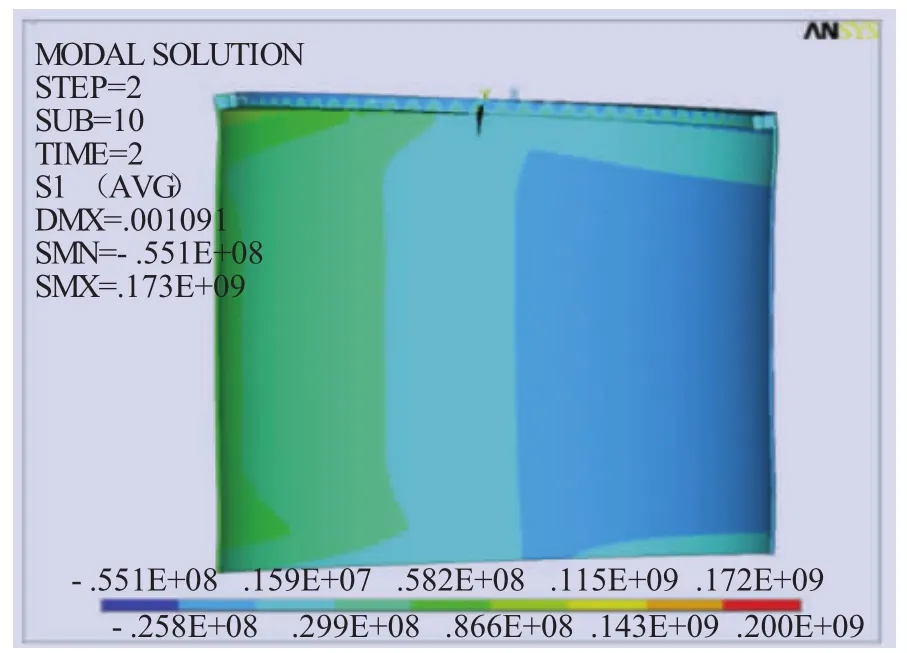
图7 塔顶法兰第一主应力图
3.4 子模型有限元分析
3.4.1 法兰受压有限元分析
在完全弯矩作用下,塔顶出现最大应力和变形,对塔顶危险区域圆角过渡处和焊缝处建立子模型进行进一步分析。如图8所示,受压测法兰圆角过渡处产生最大应力为118 MPa,筒壁上应力逐渐减小。对焊缝处进行第三主应力分析,如图9所示,法兰焊缝处产生最大压应力为-96 MPa,焊缝两侧压应力均逐渐减小,甚至在法兰连接面出现拉应力。由于焊缝仅是一圈节点,无法显示,图中代表节点的线即为焊缝。圆角最大应力大于焊缝最大应力,焊缝处相较圆角处更安全。
3.4.2 法兰受压应力集中因数计算
为确定塔顶法兰疲劳强度,需采用有限元方法分析塔顶法兰的应力集中因数。应力集中因数与名义应力σNominal相关,将σNominal分10个子步加载至法兰上,得到法兰危险应力后,计算应力集中因数。实际应用中,根据应力集中因数随法兰厚度、高度等参数的变化进行结构优化,以期在结构合理的基础上获得最小的应力集中因数。
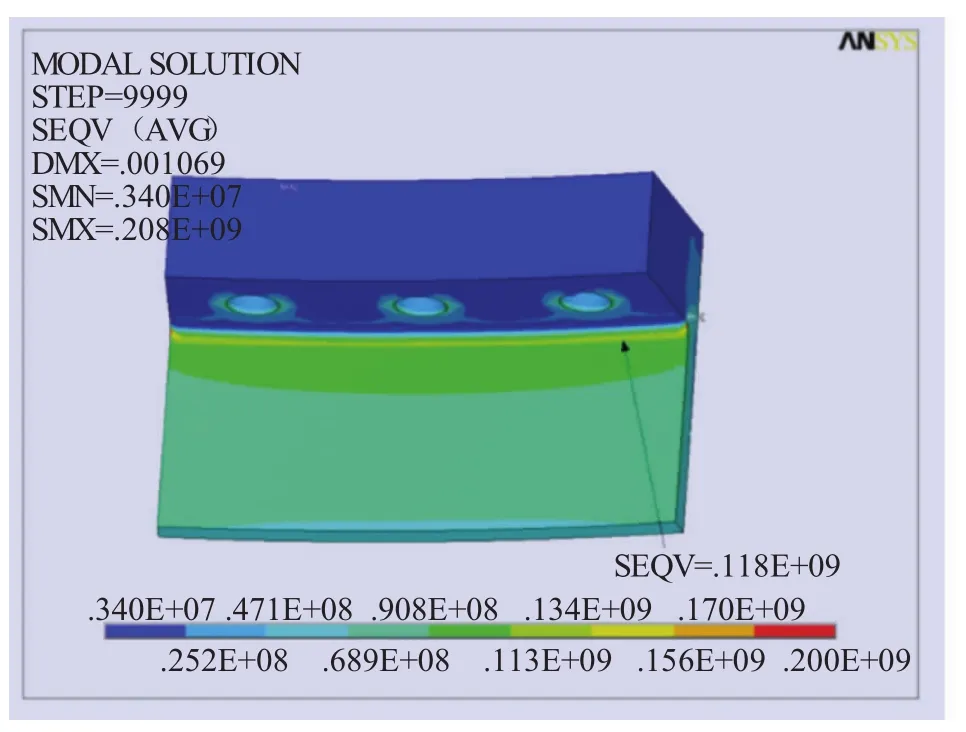
图8 法兰受压应力图
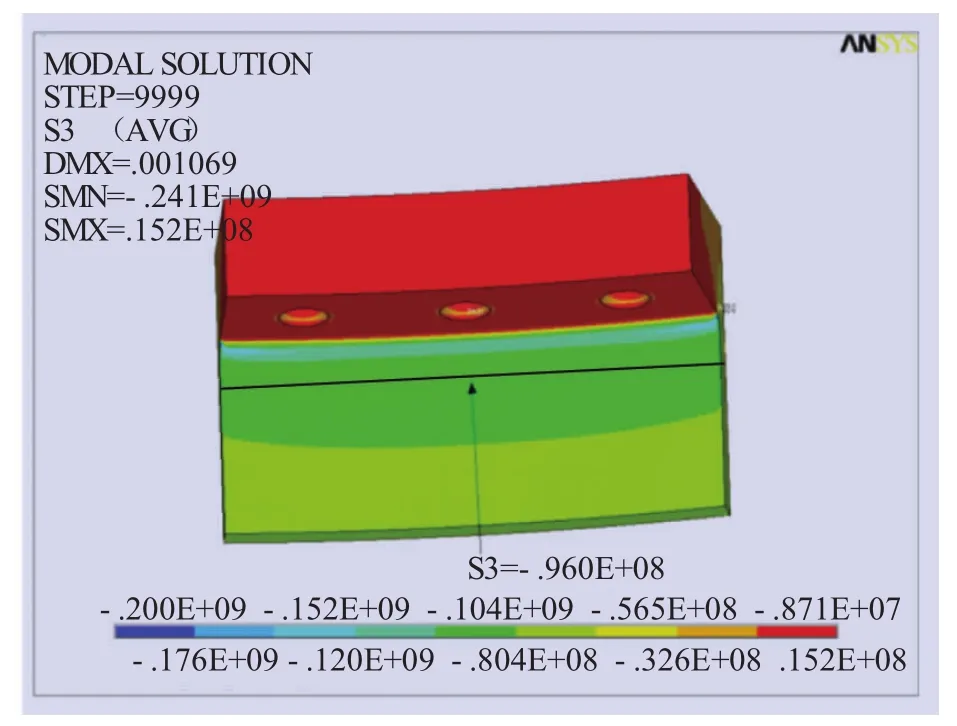
图9 法兰受压焊缝第三主应力图
应力集中因数主要针对危险位置进行计算。法兰易在圆角过渡处和焊缝处产生应力集中,因此主要分析法兰圆角和焊缝处的应力集中因数。应力集中因数K的计算基于名义应力和极限载荷作用下的法兰应力,有:

式中:σmax(t)为第t子步最大应力;σmax(0)为初始最大应力。
根据加载的极限弯矩,σNominal为63.04 MPa。
分别计算每个加载子步下的应力集中因数,得受压侧焊缝和法兰圆角处应力集中因数曲线,分别如图10、图11所示。
对受压侧应力集中因数进行研究,发现无论是圆角处还是焊缝处的应力集中因数,均随加载载荷的增大而逐渐减小,并最终趋于稳定。这是由于受压侧的法兰变形、随应力增大而趋于稳定,焊缝和圆角处应力亦逐渐趋于稳定。圆角处应力集中因数相比焊缝处较大,实际应用中需加大过渡圆角半径,同时加厚法兰壁,以达到增强法兰强度的效果。
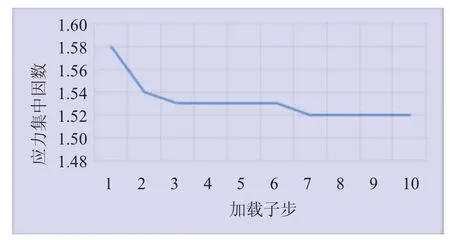
图10 受压侧焊缝应力集中因数曲线
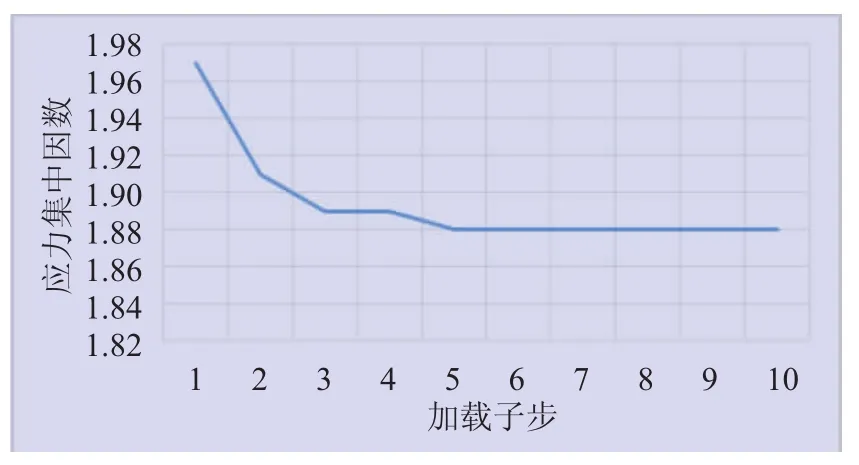
图11 受压侧法兰圆角处应力集中因数曲线
3.4.3 法兰受拉有限元分析
在完全弯矩作用下,图12和图13分别显示了法兰受拉应力和焊缝第一主应力,其中圆角过渡处为危险区域。法兰圆角过渡处产生最大应力为129 MPa,筒壁上应力逐渐减小,且法兰连接面应力迅速减小。法兰焊缝处产生的最大拉应力为103 MPa,焊缝两侧压应力均逐渐减小。由于筒壁连接处较薄,受力集中较严重,筒壁连接处应力减小速度小于法兰连接面。
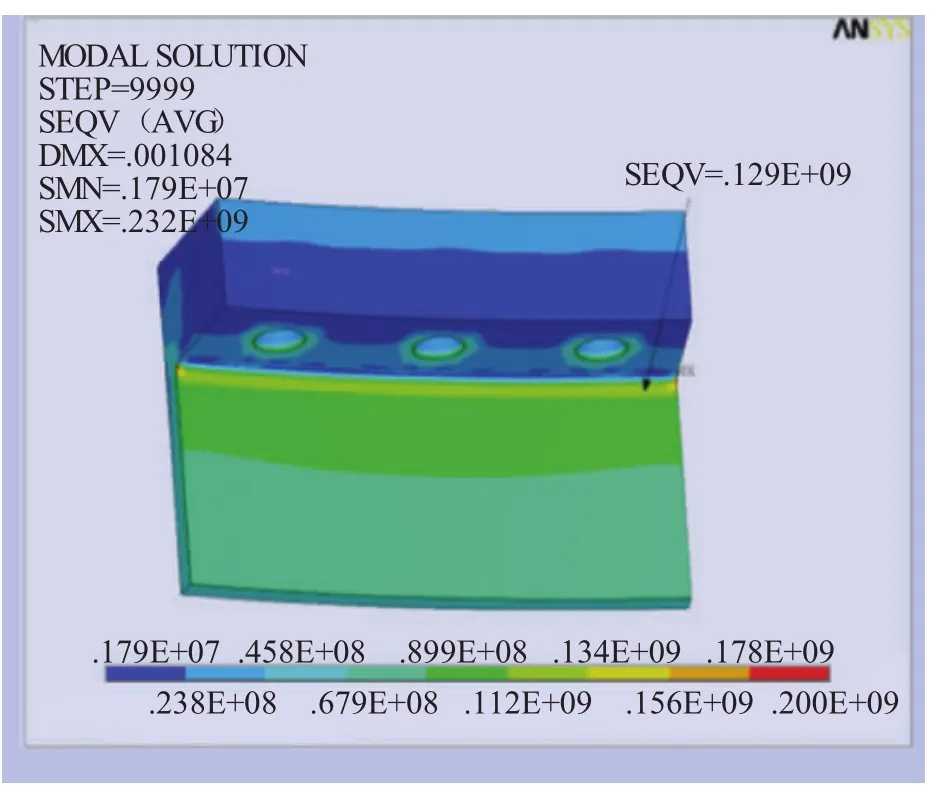
图12 法兰受拉应力图
3.4.4 法兰受拉应力集中因数计算
根据有限元计算原理,采用与受压侧应力集中因数相同的计算方法,对法兰受拉应力集中处进行
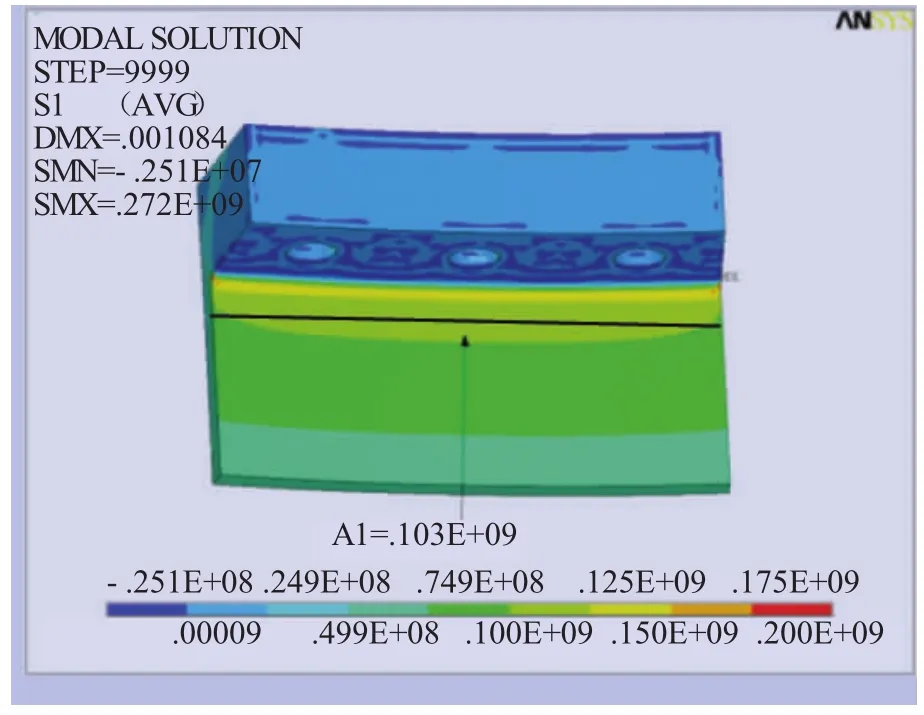
图13 法兰受拉焊缝第一主应力图
应力集中因数计算,得到受拉侧焊缝和法兰圆角处应力集中因数曲线,分别如图14、图15所示。
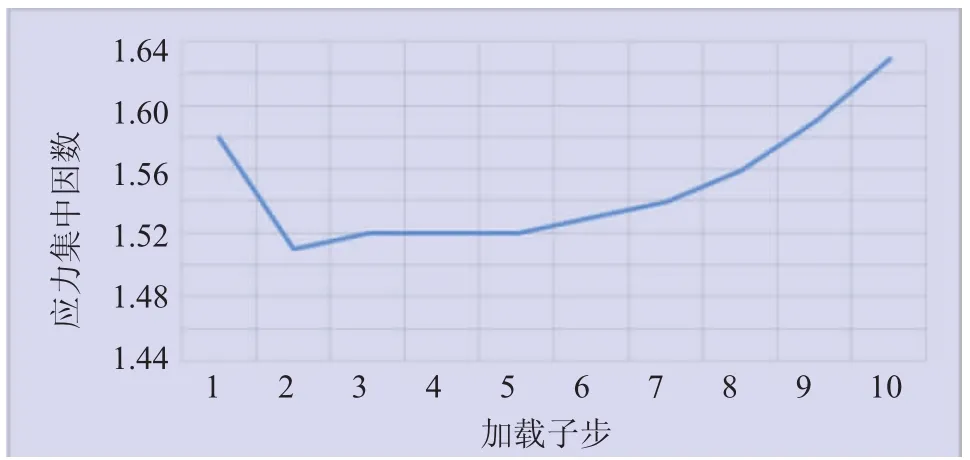
图14 受拉侧焊缝应力集中因数曲线
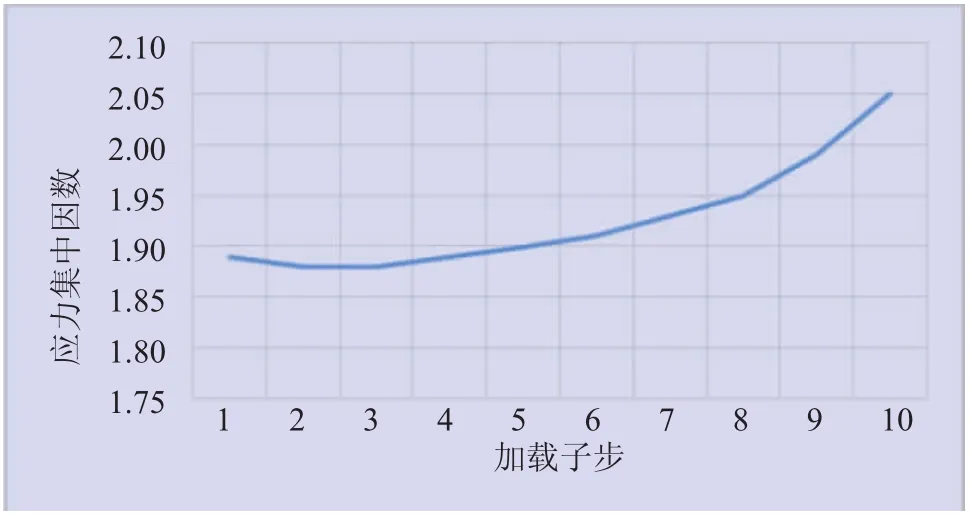
图15 受拉侧法兰圆角处应力集中因数曲线
根据应力集中因数计算结果确认,随着所加载荷逐渐增大,应力集中因数逐渐增大,但是圆角处应力集中因数大于焊缝处,说明焊缝处相比圆角处较安全。因此,在实际应用中,需要对法兰倒角进行深入优化,强化法兰的安全性能。
4 结论
根据对塔顶法兰的理论分析,发现法兰在弯矩作用下易发生压缩和拉伸变形。针对不同变形进行应力分析,确认在弯矩作用下法兰受拉侧较受压侧受力大,受拉侧间隙产生在两法兰外侧,而受压侧间隙产生在两法兰内侧。
进一步进行有限元分析,确认法兰拉伸变形较压缩变形大,且危险处圆角和焊缝处应力集中因数较大;无论是拉伸还是压缩,法兰圆角处应力集中因数均大于焊缝处;受压法兰应力集中因数随载荷加载逐渐增大后趋于平稳,进一步说明法兰受压侧相比受拉侧较安全。可见,有限元模拟与理论分析一致。为增强法兰抗疲劳强度,实际应用中需要提高圆角处强度,如采取增大圆角半径、提高圆角处光滑度和增大圆角处法兰厚度等方法。针对焊缝处应力集中,应采用焊缝加强条,并提高焊接效果。
[1] 朱仁胜,刘永梅,蒋东翔,等.基于MW级风力发电机塔架的有限元分析[J].机械设计与制造,2011(5):104-106.
[2] 周宏丽.风力发电机组法兰连接系统结构分析研究[D].重庆:重庆大学,2012.
[3]BURTON T.风能技术[M].武鑫,译.北京:科学出版社,2007.
[4] 杨广雪,谢基龙,周素霞.4D轴货车焊接构架的疲劳强度分析方法[J].北京交通大学学报,2009,33(1):24-27.
[5] 朱涛,高峰,张步良,等.汽车结构中焊缝疲劳寿命预估[J].汽车技术,2006(10):37-40.
[6] 曹广启,陈恩,季剑.法兰间隙对塔筒连接螺栓疲劳寿命的影响分析[J].装备机械,2015(4):25-29.
[7] 西北工业大学机械原理及机械零件教研室.机械设计[M].8版.北京:高等教育出版社,2006.
[8] 艾伯哈特,胡斌.现代接触动力学[M].南京:东南大学出版社,2003.
[9] 王秋芬,黄方林,张刘刚.基于Ansys的大型风电机组偏航连接系统计算方法研究[J].机械强度,2011,33(4):607-612.
[10]Germanischer Lloyd Industrial Services GmbH.Guideline for the Certification ofWind Turbines:Edition2010[S].

