花生不同光响应曲线拟合模型的比较

刘瑞显，王晓婧，杨长琴，张国伟，沈 一，刘永惠，沈 悦，陈志德

(江苏省农业科学院经济作物研究所，江苏 南京 210014)

花生(ArachishypogaeaL.)是我国产量最高的油料作物[1]，种植区域广泛，南北跨度超过34个纬度，东西跨越58个经度，种植区内耕作制度、种植模式、气候生态条件多样。此外，由于间作套种可充分利用土地资源、光热资源，在黄淮海、长江流域等花生主产区，花生与小麦、玉米等作物间套种的面积亦逐年扩大[2]，导致花生生育期内冠层光照变化幅度较大。因此，探讨花生光合特性对不同光照强度的响应机制对花生引种、品种选育以及栽培技术研究均具有重要的意义。

光合作用是植物将光能转换成可用于生命过程的化学能并进行有机物合成的生物过程。而净光合速率(Pn)是研究植物生长状况的一个重要指标[3]。影响Pn的主要因素有CO2浓度、光照强度和温度，而光照强度是最重要的[4]。为研究Pn和光合有效辐射(I)之间的关系，研究者通过建立Pn对I响应的数学模型(或光响应曲线)来解析饱和光强(Isat)、最大净光合速率(Pnmax)、光补偿点(Ic)、暗呼吸速率(Rd)和表观量子效率(α)等重要光合参数。前人已建立多个光响应曲线的数学模型，最常用的模型有直角双曲线模型[5]、非直角双曲线模型[6]、直角双曲线修正模型[7]、指数模型[8]、指数改进模型[3]。在直角双曲线模型、非直角双曲线模型和指数模型这三个模型中，当I≥0时，Pn随I的增加而增大，因此，这三个模型不能直接模拟出Isat、Pnmax[9-10]。为此，有学者[11]提出利用低光照强度下的混合模型计算Isat，但通过该方法求得的Isat远远低于实际观测值，而Pnmax远远大于实测值[10-11]。

因此，这些模型不适合处理高光合有效辐射条件下的光合数据，且不能准确地描述强光下的光抑制和光饱和现象。2007年我国学者叶子飘[9]在直角双曲线光响应模型的基础上提出了直角双曲线修正模型，2012年陈卫英等[3]在指数模型的基础上提出了指数改进模型，这两个模型均能够较好地克服直角双曲线、非直角双曲线和指数模型的缺陷，准确地拟合植物光合光响应过程及其特征参数，拟合结果与实测数据的符合程度较高。

在植物光合—光响应特性研究中，首先要选择合适的数学模型来拟合光响应曲线。只有采用正确的光合-光响应曲线模型才能计算得到准确的Pnmax、Isat、Ic及α等衡量植物光合能力的重要光合参数，才可能为后续的研究提供可靠数据[12]。由于不同植物对光照强度变化的敏感度及响应方式存在较大差异，因此不同植物的最适光合-光响应曲线的模型也不尽相同[13]。

目前，有关花生光合—光响应模型的研究鲜有报道。为此，本研究拟采用不同的模型拟合2个花生品种的光响应曲线，以此对比分析不同模型在花生光合特性研究上的拟合度及潜在问题，为进一步推动光合作用光响应曲线在花生光合生理生态研究中的应用提供依据。

1 材料与方法

1.1 供试材料

2017年在江苏省农科院网室内进行盆栽试验。将田间土壤自然风干、过筛去杂后与河沙按照体积比1∶1混匀后作为供试花生种植土壤。供试花生品种为泰花5号(Tai-5)与中花16号(Zhong-16)。5月25日，每个品种选择籽粒大小均匀且健康无病虫害的花生籽粒播种于盆钵中，每盆播种3粒。试验所用盆钵直径30cm，高25cm，每盆装土约10kg。待花生3叶期时，每盆留健壮植株1株。每个品种重复15次，每盆为1个重复。将花生置于网室内，所有管理均按高产栽培要求进行。

1.2 光响应数据的测定

待花生长至8叶期时，选择晴天9:00-11:00用便携式光合仪LI-6800(LI-COR， Lincoln，USA)测量净光合速率(Pn)。CO2浓度控制在380±2 μmol·mol-1，温度控制在34±2℃，选用光合仪内置光源将光合有效辐射(I)设置为2000、1600、1200、1000、800、600、400、200、100、50、20、0 μmol·m-2·s-1，测定Pn。每个光照强度等待3min。测定部位为主茎倒3叶，每次每个品种测定4次。

1.3 光响应模型介绍

1.3.1 直角双曲线模型

直角双曲线模型[14]的数学表达式为：

其中Pn为净光合速率，I为光强，α为植物光合作用对光响应曲线在I=0时的斜率，即光响应曲线的初始斜率，也称初始量子效率。Pnmax为最大净光合速率，Rd为暗呼吸速率。式(1)是一个没有极值的函数，也即直角双曲线是一条没有极点的渐近线。因此，由式(1)无法求得饱和光强(Isat)。为了估算Isat，根据叶子飘[15]介绍，需用直线方程拟合弱光强条件下(≤200 μmol·m-2·s-1)的表观量子效率(apparent quantum efficiency, AQE)，利用非线性最小二乘法估算Pnmax，然后求解直线方程式(2)得到Isat。

Pnmax= AQE×I-Rd…… (2)

1.3.2 非直角双曲线模型

光响应曲线的非直角双曲线模型[16]的表达式为：

公式中Pn、α、I、Pnmax、Rd的定义均与直角双曲线模型相同。θ为反应光响应曲线弯曲程度的曲角参数，取值范围为0<θ≤1。由此可见公式(3)仍是一个没有极值的函数，无法直接求解Isat，其求解方法与直角双曲线模型相同。

1.3.3 指数函数模型

光响应曲线的指数函数模型比较多。本文采用Bassman和Zwier[17]提出的指数函数模型，其表达式为：

Pn=Pnmax(1-e-αI/Pnmax)-Rd…… (4)

公式中Pn、α、I、Pnmax、Rd的定义均与直角双曲线模型相同，e为自然对数的底。通过式(4)可求取光补偿点(Ic)，但无法求取Isat，要估算Isat，需要假设光合速率为0.9Pnmax或0.99Pnmax对应的光强为饱和光强[18-19]。

1.3.4 直角双曲线修正模型

中国学者叶子飘[15]提出了直角双曲线的修正模型。其表达式为：

式中α、I、Rd的定义均与直角双曲线模型相同，β为光抑制系数，γ为光饱和系数[20]。式(5)是一个具有极值的函数，因此，由式(5)可直接求出Pnmax、Isat、Ic。同时可拟合具有光抑制的光响应曲线。

1.3.5 指数改进模型

为改进光响应曲线指数模型无法准确计算出光饱和点和最大净光合速率的缺陷，陈卫英等[3]提出了指数改进模型。其表达式为：

Pn=be-cI-de-fI…… (6)

其中Pn为净光合速率，I为光强。对式(6)进行解析Pnmax、Isat、Ic、Rd：

Rd=b-d

α= -bc+df

Pnmax可由求出的Isat代入(6)中求出。

1.4 数据处理

试验数据处理及作图由Excel 2007 完成，模型分析由SPSS 11.5 软件分析。

2 结果与分析

2.1 光响应曲线的拟合及其比较

图1可见，除直角双曲线模型的拟合值与实测值差别较大外，其余四个模型的拟合值均与实测值较为接近。因此从直观看，采用非直角双曲线模型、指数模型、直角双曲线修正模型、指数改进模型都可较好拟合其实测点。图1进一步可看出，两品种的Pn均在1200～1600 μmol·m-2·s-1达到饱和值，而后Pn随I的增加变化较小。

2.2 不同花生光合—光响应曲线模型参数比较

由表1可见，所有模型拟合的初始量子效率(α)均在0≤α≤0.125 范围之内，直角双曲线模拟的泰花5号的α最大，为0.114。

不同模型拟合的两个品种的最大净光合速率(Pnmax)均比实测值高，但以直角双曲线修正模型和指数改进模型的计算值最为接近实测值，指数改进模型略优于直角双曲线修正模型。泰花5号Pnmax的指数模型和非直角双曲线模型的拟合值以及中花16号的Pnmax的直角双曲线模型的拟合值与实测值相差较大。

对于饱和光强(Isat)，两个品种由直角双曲线与非直角双曲线通过直线方程求解得到的Isat均不到实测值的1/2，远小于实测值，而由指数函数、直角双曲线修正模型与指数改进模型求解的Isat与实测值差异较小，并且指数改进模型和直角双曲线修正模型可通过模拟直接计算两品种的Isat。

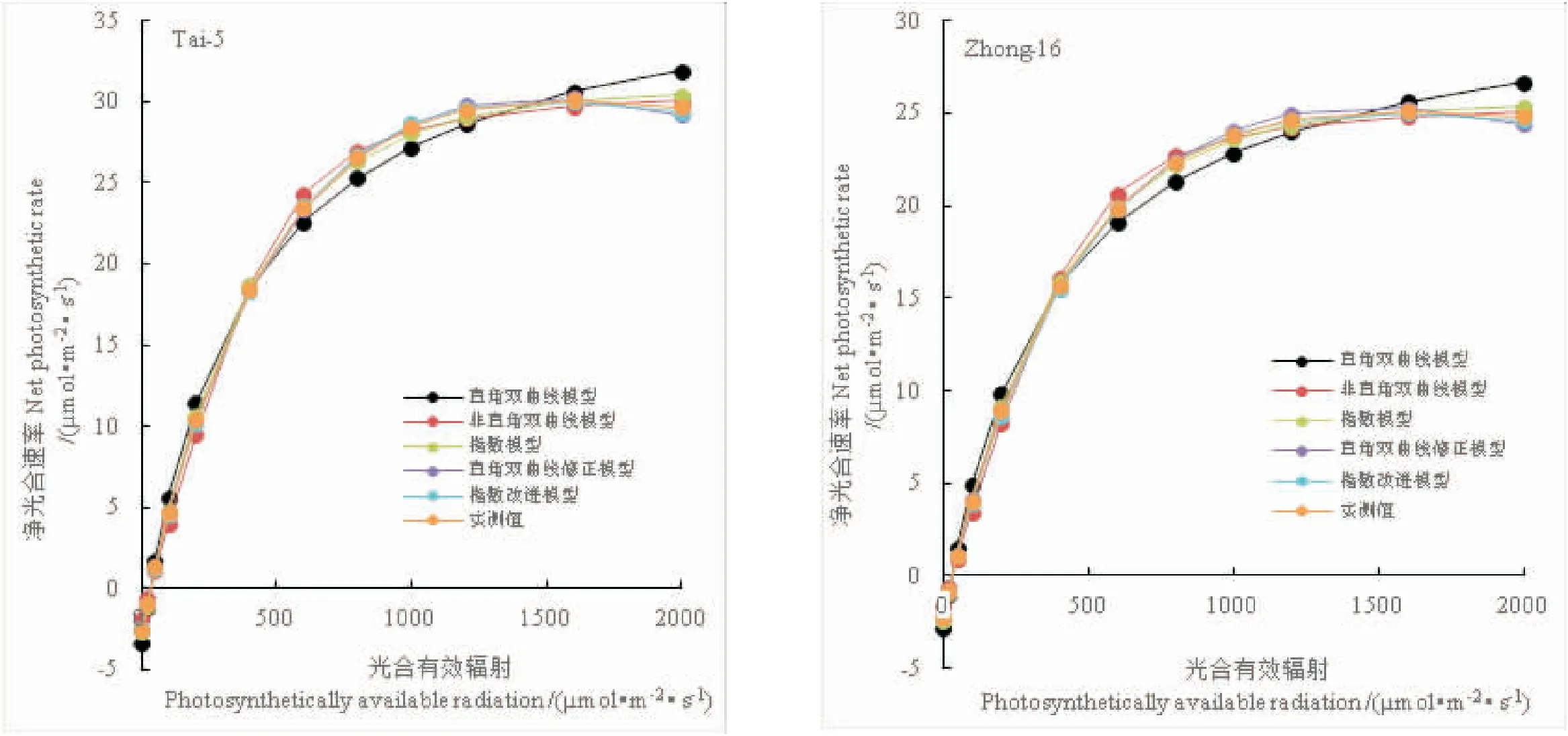
图1 不同模型拟合的2个花生品种光响应曲线 Fig.1 Light response curves fitted by different models for 2 peanut varieties

品种Varieties模型 ModelαPmaxIsatIcRdr2其他Other 直角双曲线模型Rectangular hyperbola model0.114031.476742.9931.4803.3100.990 非直角双曲线模型Nonrectangular hyperbola model0.059033.020739.3127.9701.8250.9990.906(θ)泰花5号指数模型 Exponential model0.085433.3501556.6533.1702.7150.998 Tai-5直角双曲线修正模型Modified rectangular hyperbola model0.082030.3001495.3032.0002.5140.9990.001161(γ)0.000179(β)指数改进模型Modified exponential model0.080730.2661469.3731.0992.4260.996 实测值 Measured value ≈29.7≈160020～50≈2.12 直角双曲线模型Rectangular hyperbola model0.100034.690716.8431.3102.8720.990 非直角双曲线模型Nonrectangular hyperbola model0.051927.632624.2128.7481.6470.9990.906(θ)中花16号指数模型 Exponential model0.074527.8951575.8133.3102.3750.998 Zhong-16直角双曲线修正模型Modified rectangular hyperbola model0.072625.4001482.5032.2002.2300.9980.001281(γ)0.000173(β)指数改进模型Modified exponential model0.068625.0801496.3432.6602.1580.996 实测值 Measured value ≈24.87≈160020～50≈1.56

注：α, 初始量子效率(mol CO2mol-1photons);Pnmax, 最大光合速率(molm-2s-1)；Isat, 饱和光强(molm-2s-1);Ic, 光补偿点(molm-2s-1)；Rd，暗呼吸速率(molm-2s-1)；r2，决定系数。

Note: α, initial quantum yield;Pnmax, maximum net photosynthetic rate;Isat, light saturation point;Ic, light compensation point;Rd, rate of dark respiration;r2, determination coefficient.

所有模型拟合的光补偿点(Ic)差异较小，均在实测值范围内，但两品种的Ic以非直角双曲线的拟合值最低。不同模型拟合的暗呼吸速率(Rd)与实测值接近度不一致。对于泰花5号以直角双曲线修正模型和指数改进模型拟合的Rd较接近实测值，而中花16的Rd以非直角双曲线的拟合值最接近实测值。表1进一步仍可见，5个模型求得的决定系数r2均高于0.99，说明其拟合程度均非常高。

在直角双曲线修正模型中，有两个非常重要的参数，γ为光饱和项，β为光抑制项，并且可通过模拟计算直接求出。由表可见泰花5号的γ值小于中花16，而β值大于中花16。

2.3 不同花生品种的光合特性

由图1 和表1进一步分析可见，泰花5号的光合特性优于中花16号，表现在同一光强下，泰花5号净光合速率高于中花16号。

3 讨 论

由各模型公式可知，直角双曲线模型、非直角双曲线模型和指数函数是3个没有极值的方程，在定义域范围内，Pn始终随着I的增加而增加。因此，这3个模型不能拟合植物出现光抑制时的光响应曲线，并且由这3个模型不能直接模拟出Isat，必须通过非线性最小二乘法估算Pnmax(直角双曲线模型与非直角双曲线模型)或者假定0.9Pnmax对应的光合有效辐射，但是通过这种方法求得的Pnmax和Isat均与实测值差异较大。本研究发现，用直角双曲线模型、非直角双曲线模型和指数模型拟合的2个花生品种的Pnmax均远高于实际观测值，而直角双曲线与非直角双曲线模型求得的Isat只有观测值的1/2。这与前人的研究结果[10-12]相一致。这说明直角双曲线模型、非直角双曲线模型和指数函数不适合用于拟合花生的光响应曲线。

直角双曲线修正模型是一个存在极值的方程，因此可拟合植物存在光抑制时的光响应曲线。图1可见，两个花生品种的Pn均在1200～1600 μmol·m-2·s-1达到饱和值，而后Pn随光强的增加而不再增加，直角双曲线修正模型的拟合曲线与实测曲线符合度非常高。2012年叶子飘与康华靖[20]对直角双曲线模型参数的生物学意义进一步明确。在此模型中，β为光抑制项，γ值一定时，β值越大，光响应曲线弯曲程度就变大，表示光系统Ⅱ(PSⅡ)天线色素分子吸收光量子的截面与PSⅡ天线色素分子处于激发态的平均寿命的乘积越大，植物受光抑制就越强。而γ为光饱和项，当β一定时，γ值越小，表示光响应曲线弯曲程度就越小，植物越不容易发生光饱和现象，对应饱和光强的值越大。

由表1可以看出，泰花5号的β值略大于中花16，而γ值小于中花16，据此分析，泰花5号较中花16号不易出现光抑制现象，这与泰花5号的饱和光强(1495 μmol·m-2s-1)高于中花16号(1482 μmol·m-2s-1)是一致的。可见，直角双曲线修正模型可为进一步研究花生逆境胁迫下的光抑制现象，这是其他模型所不具备的。

指数改进模型是陈卫英等[3]在指数模型的基础上提出的，本研究中由该模型计算的各个光合参数与实测值非常接近，这说明该模型同样可以用于花生光合光响应的研究中。虽然指数改进模型不能通过计算直接求出光饱合项或光抑制项，但该模型可以准确计算出花生光饱和点与最大净光合速率，这也为研究高光照强度下的光抑制现象提供了快速准确的方法[3]。

综上所述，在花生光合—光响应的研究中可以选择直角双曲线修正模型和指数改进模型进行曲线的拟合。这两个模型均具有很好的拟合性，拟合结果准确，尤其是当高光强存在时，可以拟合花生存在光抑制时的光响应曲线。