变曲率摩擦摆隔振技术在桥梁抗震中的研究与应用★

项敬辉　冯克岩　孙　刚

(1.天津市市政工程设计研究院，天津　300457；　2.同济大学，上海　200092)

0　引言

近年来工程隔震技术有了快速发展，隔震技术的目的是为了将结构与地震激励分离开来，其基本原理是在基础结构和上部结构之间设置隔震层并利用隔震装置的耗能能力消耗地震输入能量，同时控制隔震结构的位移幅值，从而降低结构的动力学响应，达到对结构的保护作用[1]。传统意义上的摩擦摆式支座(FPB/FPS)的滑动面均为等曲率曲面，一旦球面半径确定，其隔震周期也随之确定，而在近断层常伴有长周期脉冲型地震波，容易与隔震结构发生低频共振。为克服这一缺陷，不少专家或学者将滑动球面换成函数曲面，研发出变曲率摩擦摆式隔震支座，它的曲率半径在整个滑动区域并非定值，因此隔震周期会随着位移不断改变，可避免共振现象的发生[2,3]。

1　理论分析

变曲率摩擦摆单摆隔震支座的滑动曲率半径是随着隔震支座中心位置改变的连续函数，当支座离中心位置越远，其曲率越大而隔震周期随之延长，滑动面的曲面函数由椭圆方程转化而来，可表示成[4]：

(1)

其中，b为椭圆的短轴长；d为与椭圆长轴和支座位移相关的一个常数。

将式(1)中曲面函数一次微分后可得曲面的切线斜率：

(2)

由图1可知，随着b值增大，曲面斜率整体统一增大；随着d值的增大，小位移处曲面斜率减小，大位移处曲面斜率增大[5]。

2　数值模拟分析

2.1　摩擦摆支座模型及分析设置

为研究等曲率和变曲率摩擦摆支座的滞回性能差异，采用通用有限元分析软件Abaqus V6.10进行支座模型的建立，支座模型包括摩擦摆滑动曲面和球摆两种构件，图2给出了支座模型的剖面示意图。

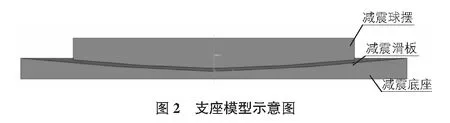
支座根据减震滑板滑动曲面不同分为变曲率摩擦摆隔震支座与等曲率摩擦摆隔震支座。等曲率摩擦摆和变曲率摩擦摆支座在平衡位置处的曲率半径相等，也即隔震周期相等。摩擦摆支座的减隔震周期定为2.5 s，也即平衡位置处曲率半径为1.55 m。

变曲率摩擦摆隔震支座的滑动曲面函数为：

等曲率曲面函数为：

摩擦摆支座模型竖向加载方式为平面均布压强加载，水平方向采用位移时程加载方式。水平加载时程曲线如图3所示。

2.2　摩擦摆支座模型的影响分析

摩擦摆支座的竖向承载力主要由聚四氟乙烯板的压强控制，但聚四氟乙烯的机械强度较低，仅为14 MPa～32 MPa，其抗压强度相对支座其他部件的钢材来说仍非常有限，仍是支座竖向承载力的控制部分。而支座模型中的减震球摆的尺寸决定了聚四氟乙烯板的受压面积，从而决定了整个摩擦摆支座的竖向承载力。

对比不同尺寸的减震球摆对摩擦摆支座模型的影响分析，按照图3所述的加载方式进行低周反复时程加载，分析减震球摆尺寸对等曲率摩擦摆和变曲率摩擦摆的性能影响。

由图4，图5可知，减震球摆的尺寸对等曲率摩擦摆支座的滞回特性基本没有任何影响，表现为双线性的滞回曲线的特征；减震球摆的尺寸对变曲率摩擦摆支座的滞回特性影响较大，总体表现为：球摆尺寸越大，滞回曲线的屈服后刚度和有效刚度越小,球摆尺寸对其线性刚度基本无影响。

变曲率摩擦摆的屈服后刚度和有效刚度均小于等曲率摩擦摆，并且当球摆尺寸越小，变曲率摩擦摆和等曲率摩擦摆的刚度差异就越小，也即当球摆越小两种摩擦摆支座的差异就越小。

在实际桥梁工程中，通常需要支座的竖向承载力足够大，也就限制了球摆的尺寸不能够做的太小。上述模型分析中均是按照图3所示的水平位移时程加载的，最大位移设置为0.15 m，主要是因为实际摩擦摆支座的球摆尺寸较大，发生0.15 m水平位移时基本已经滑移到底座减震滑板的边缘，所以不允许支座发生较大的位移。

如果可以将球摆尺寸做到较小，则支座的水平最大位移限值可以比0.15 m大很多，现将小尺寸球摆模型的最大水平位移放大1倍后进行计算分析，如图6，图7所示。

由图6，图7可知，当水平位移限值放大1倍后，等曲率摩擦摆滞回曲线仍表现为双线性模型，但变曲率摩擦摆滞回曲线已表现出比较明显的非线性特性，这跟邓雪松，龚健和周云所作《变曲率摩擦摆隔震支座理论分析与数值模拟》一文中的变曲率滞回曲线基本一致，也证实了计算模型的正确性。从图中可以直观地得出变曲率摩擦摆相对等曲率摩擦摆具有明显的刚度软化特性。

2.3　变曲率摩擦摆支座的数值模拟

在实际桥梁工程中，摩擦摆支座的减震球摆直径0.4 m～1.6 m，所以水平位移限值是比较小的，如图6，图7所示的非线性滞回特性和刚度软件特性是不能实现的。变曲率摩擦摆实际呈现的滞回特性仅仅表现为双线性的滞回特性，与等曲率摩擦摆的滞回特性基本一致，只是滞回曲线在数值上与等曲率摩擦摆有所区别，也即变曲率摩擦摆相对于等曲率摩擦摆仅仅是屈服后刚度和有效刚度较小的双线性滞回模型。

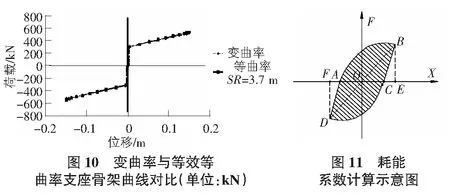
既然变曲率支座的滞回曲线与等曲率支座滞回曲线均表现为双线性滞回模型，则若选择一曲面高度变化差距不大的等曲率支座与其对比，根据摩擦曲面高度相等的原则，可以计算出等效的等曲率支座的曲率半径为3.7 m，曲面对比图见图8，滞回曲线对比图见图9，图10。从图中可以发现，变曲率摩擦摆支座在±0.15 m范围内其滞回性能与等曲率支座(摩擦曲面高度相等，SR=3.7 m)相差无几。

2.4　滞回性能指标对比

耗能性能可用耗能系数来反映，根据JGJ/T 101—2015建筑抗震试验规程第5.5.6条规定，耗能系数计算公式见式(3)：

(3)

等效粘滞阻尼器系数He可按如图11所示滞回曲线ABCD的面积来计算：

(4)

等效粘滞阻尼系数与耗能系数的关系为：

(5)

如表1所示仅给出球摆直径为0.8 m的支座性能参数。

表1　滞回性能指标对比

3　结语

文章对等曲率和变曲率摩擦摆支座进行了系统的分析，得到结论如下：

1)等曲率摩擦摆减震球摆的尺寸对支座的滞回性能基本没有影响，而变曲率摩擦摆减震球摆的尺寸会对支座的滞回产生比较明显的影响，整体表现为减震球摆直径越大，骨架曲线的屈服后刚度和有效刚度越小。

2)在设计位移范围内(±0.15 m范围内)骨架曲线基本表现为双线性折线模型，不能体现变曲率摩擦摆支座的强非线性和刚度软化的特点，只有当减震球摆尺寸较小且位移较大时才能得到跟理论变曲率摩擦摆支座类似的滞回性能。

3)在设计位移范围内变曲率摩擦摆支座的骨架曲线跟等曲率摩擦摆支座类似，均为双线性折线模型，故可以采用摩擦曲面高度相等的等曲率摩擦摆代替变曲率摩擦摆支座，并且得到的滞回性能非常接近，在有限元分析中，可以用等效的普通摩擦摆支座去模拟变曲率摩擦摆支座。

参考文献:

[1]李大望，周锡元，王东巧.摩擦摆系统振动性态的进一步分析[J]．振动工程学报，2001,14(3)：330-333.

[2]龚健，周云.摩擦摆隔震技术研究和应用的回顾与前瞻(Ⅰ)——摩擦摆隔震支座的类型与性能[J].工程抗震与加固改造，2010,32(3)：1-10.

[3]龚健，周云．摩擦摆隔震技术研究和应用的回顾与前瞻(Ⅱ)——摩擦摆隔震结构的性能分析及摩擦摆隔震技术的应用[J].工程抗震与加固改造，2010,32(4)：1-19.

[4]龚健，邓雪松，周云．摩擦摆隔震支座理论分析与数值模拟研究[J]．防灾减灾工程学报，2011，31(1)：56-62.

[5]陈永祁，杨凤利，刘林.摩擦摆隔震桥梁的设计及应用[J].工业建筑，2009(3):45-49.

[6]吴宜峰，李爱群，王浩．连续梁桥摩擦摆支座参数分析与优化[J]．桥梁建设，2015，45(1)：20-25.