有热源巷道风流温度分布非稳定模型及数值计算*
李宗翔,刘 宇,刘汉武,林 琳
(1.辽宁工程技术大学 安全科学与工程学院, 辽宁 阜新 123000;2.矿山热动力灾害与防治教育部重点实验室, 辽宁 阜新 123000 )
0 引言
有热源巷道风流温度分布非稳定计算,是灾变时期(热害或火灾)矿井通风网络温度仿真计算的基础和关键性问题[1-5]。有热源巷道指的是巷道或工作面中设有大功率机电设备(放热)或制冷设备(吸热、负热源)或巷道火灾火源放热等,属于典型流体分支中源的问题[6]。当风流从热源经过,温度发生变化,热源升温,冷源降温。温度在井巷风流中的传播属于有热源的风流对流-扩散-换热非稳定过程。如果是单一条巷道或局部网巷道问题,可运用Fluent软件对3D巷道空间模型进行精度更高的仿真计算[7],多数火灾的仿真计算是按公式法计算温度[8-9]。有热源且非稳定问题,初始温度不是均匀分布就不能简单套用解析式来计算。更复杂情况,如机电设备开停热源时断时续、火灾燃烧强度不断变化或风流紊乱等,都将形成非稳定-非均匀的温度分布,此时,必须用二阶微分方程来描述,用差分数值方法求解[9-12]。在矿井火灾计算中,火源都是按温度值(1类条件)给出[11-13]。这里讨论有热源巷道非稳定风流温度二阶微分方程及有限元方法求解,解决热源按放热强度(2类热流量条件)给出的热源项处理算法,并将算法组构到网域中,实现对全矿井风流温度分布计算等一系列问题做进一步研究。
1 有热源单一巷道风流温度非稳定基本方程
被加热的风流(或高温烟流)一方面随风流整体移动,另一方面由于温度梯度和风流脉动作用,在风流中逐渐弥散,产生温度传导和扩散,同时热风流又与巷道围岩产生热交换。
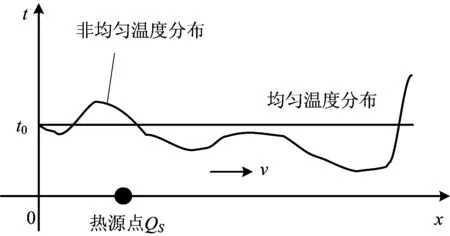
图1 通风巷道热源与风流温度分布Fig.1 Distribution of lane heat source and temperature in the ventilation tunnel
如果是在全矿复杂网域的背景下计算单一巷道问题,仍离不开一维井巷模型。通风巷道热源与风流温度分布情况如图1所示,如果一维井巷通风风流的初始温度分布是均匀、稳定条件的计算,可根据风流与围岩热交换,建立风流温度一阶线性非齐次微分方程,求解方程导出稳定温度分布的析解式[1]。
从矿井网络系统宏观的角度看,单一巷道风流运动可看做是一维的巷道通风对流扩散问题,矿井网络系统火灾仿真计算仍然依据这一假设[10-12],进一步假设,热源引起风流温度变化的时间,远小于长期的通风与地层之间非稳定热交换时巷道围岩温度变化时间,计算时视巷道围岩温度不变化,并忽略热湿换热影响。那么,用温度表示的热交换对流扩散微分方程为[11-12]:
(1)
式中:t为风流温度,℃;x为长度位置,m;kx为温度扩散系数,m2/s;CP为风流定压比热容,J/(kg℃);ρ为风流密度,kg/m3;tr为巷道围岩温度,℃;qS为巷道中单位时间单位体积的放热源项,J/(m3·s);若qS以J/(ms)单位形式给出,除以巷道断面积S;βf为单位时间单位体积风流与巷道之间对流热交换源项值,W/(℃· m3),即平均到单位体积中换热那部分值;τ为时间变量,s。
热源qS分为稳定热源和非稳定热源,一般稳定工作的机电设备散热是稳定热源,矿井火灾的火源燃烧强度在不断变化,一般属于非稳定热源。热源项大都是按第1类边界条件,即热源点按温度给出的;还有一种形式是以热源项给出,火源燃烧是能量释放的过程,从能量释放加以解释时,应按第 2类边界条件,即放热量给出。一般,稳定热源qS= const,非稳定热源用函数表示qS(x,τ)。
随着含烟风流的流动,热烟流与巷道围岩存在热交换。巷道风流微元体如图2所示,对一维巷道计算模型,有微分元体dx,微分元体积为 dV=Sdx,在dV中的热交换的总热流量取决于巷道壁的换热,即:
βr=arUdx
式中:ar为换热系数,W/(m2℃);U为巷道周长,m。
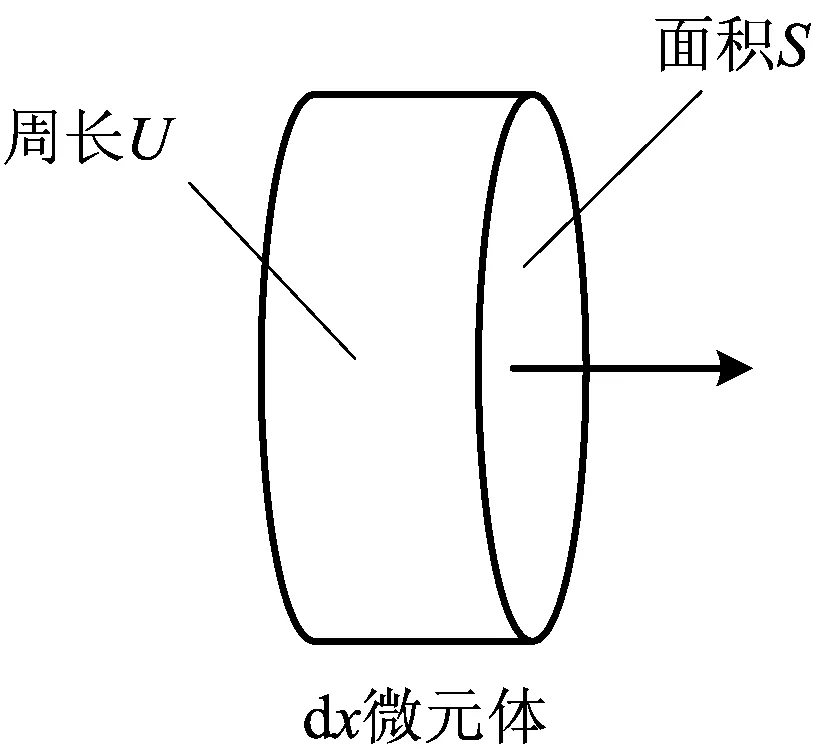
图2 巷道风流微元体Fig.2 Lane heat source microelement
平均分摊到单位体积中换热那部分值定义为:
代入式(1):
(2)
或可写成:
(2a)
式中:ar为巷道壁面换热系数,W/(m2·℃);Qt, s为井巷中单位长度上热源升温放热强度,J/(m·s)。
方程(2a)各项的单位量纲统一于[℃·s-1]。
热烟气流的机械弥散伴随着温度的传播,此外,即使不存在烟气流弥散,也存在风流空气的热传导,显然,热烟气流的机械弥散远大于空气热传导。方程中的温度扩散系数:
式中:λ为热传导系数,W/(m·℃);Ex为风上流纵向热烟气流湍流弥散热传系数,W/(m·℃)。
2 巷道对流-扩散问题的一维有限元分析
研究巷道一维对流-扩散(弥散)问题可用的方法有差分方法和有限元法,这里只讨论比较简单的有限元法[13]。若将巷道按一维考虑,根据一维有限元单元的划分,对单元e有插值函数:
Φi(x) =ai+bix,(i= 1, 2 )
(3)
式中:ai,bi为插值系数,在每个单元中应保证Φi(xi) =1,Φi(xj) =0,Φj(xj) =1,Φj(xi) =0,得到:
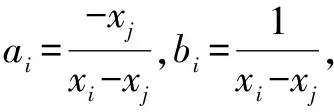
单元中浓度函数t=Φiti+Φjtj,其中ti,tj为待求的节点浓度(函数)值。
由对流扩散方程(1),相应的卡辽金积分表达式为 :
根据Green-Gauss公式,对其分部积分 :
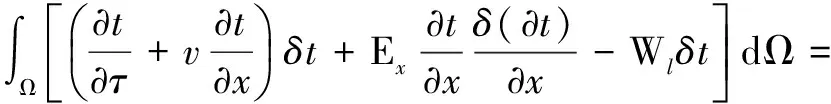
单元近似函数t(τ) =ti(τ)Φi(x) 。对e单元,有限元特征式 :
(4)
其中 :
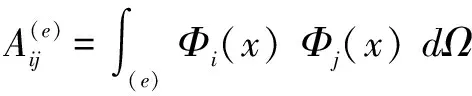
将式(3) 代入上式,积分得到 :
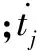
(5)
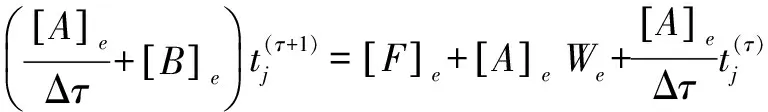
(5a)
式中:[A]e,[B]e,[F]e和We分别为单元的矩阵、源向量及右端项向量;e代表单元。
以上单元分析通过单元合成将单元叠加到整体一维区域上,得到有限元求解的线性方程组(过程略),即得到合成一维巷道中的总体方程为:
(6)
式中: [A],[B],[F]和W分别为由各单元合成的巷道总体的矩阵、源向量及右端项向量。
在MATLAB平台上实现了上述过程一条巷道的一维有限元计算机程序编制工作(TF_GasTen1a.m)。
3 单一巷道中风流非稳定温度分布模拟计算
3.1 计算的基本条件
巷道总长度为428 m,巷道参数:巷道断面积S=11.2 m2,周长U=13 m,α=0.021 kg/m3,通风风量为15.1 m3/s,风速为1.35 m/s。起点边界条件为27 ℃,风流密度1.2 kg/m3,风流热传导系数0.027 W/(m·℃);风流定压比热1 005 J/kg℃,围岩温度27 ℃;广义换热系数7 W/(m2·℃),Ex=1.35 m2/s。单元剖分尺度1.5 m(精度);热源点位置130 m,并假设:每件放热机电设备(热源)分配在一个单元的空间中,则We中的元素 :
(7)
其中,h是单元长度,m。
3.2 巷道初始温度恒定均匀分布的定解条件及求解
方程(2a)温度分布t(x,τ) 求解的定解条件为 :
边界条件:t|x=0=t(0,τ) = 27℃;
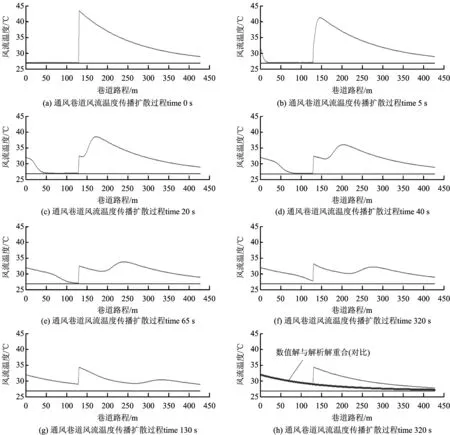
初始条件:t|τ=0=t(x, 0) = 27,0 热源项:Qs(130,τ) = 300 kW。 温度的初始分布恒定,起点边界条件是巷道入口风流温度始终保持27 ℃,有热源巷道风流温度变化过程模拟结果如图3所示。假设在流动过程中井巷风路中无外源气涌出,热源强度(机电设备功率)为300 kW。模拟时间步长取2 s,模拟结果如图4所示,给出温度的非稳定模拟的动态解。根据图3的模拟结果,风流在第175 s以后就基本趋于稳定,为使之达到充分稳定,这里以在第320 s时的温度分布作为对比,可见已经完全稳定并重合。图3(f)中的粗线是按解析法给出的解(对比)。 图3 温度均匀初始分布有热源巷道风流温度变化过程的模拟结果Fig.3 The simulation results of temperature variation of lane with heat source 在热源稳定的条件下,有热源巷道风流温度分布最终趋于稳定(见图3),但温度不是均匀分布的。在矿井火灾的灾变时期,由于风流紊乱,火灾烟流在复杂网络中传播,在某一时间点上井巷风流的温度分布也不是均匀的,存在较大的波动状态。将图3中第320 s 趋于稳定的温度分布结果作为初始条件,将起点的边界条件改为32℃,热源强度改为100 kW,其他模拟条件不变,则方程(2a)求解的定解条件为 : 边界条件:t|x=0= 32℃; 初始条件 :t|τ=0=t(x, 0),0 热源项:Qs(130,τ) = 100 kW。 风流温度计算结果如图4所示。 在温度边界条件和源改变后,在非稳定计算中,井巷温度分布重新经过一番调整变化过程,最后又达到新的稳定状态,图4(f)中的粗线温度分布是按解析法给出的一般解,显然,解析法无法实现有热源、非均匀分布的井巷风流温度分布的计算。 在解的收敛性检验方面,理论上,假设热源前的风流温度是不受热源影响的,图3和图4中的最后的一幅图给出了稳定解析解与非稳定数值计算达到稳定后的数值解的对比,热源前一段的数值解与解析解两者完全重合,说明有限元数值解的收敛性很好,计算精度满足要求。 图4 温度非均匀初始分布有热源巷道风流温度变化过程的模拟结果Fig.4 The simulation results of the temperature change process of the lane with heat source 1) 数值模拟描述了有热源巷道风流温度的平移和扩散的流动传播过程。将井巷中设备热源(或制冷负源)作为源项,以热强度(热流量)条件给出,构建了巷道风流温度分布非稳定变化求解方程的热源表达方法。数值计算实现了有热巷道温度分布随时间和位置的变化。强调指出,随着热源能量的传播,经过长时间或传播距离的增长而逐渐趋于稳定;矿井热害主要决定因素还是地层温度,设备热源对风流温度影响与变化最终稳定于地层温度。 2) 提高计算精度是仿真计算的基本要求。数值计算的误差原因是时间和空间剖分离散的误差导致的,考虑到井巷各地点的分支风量变化很大,宜于采用自动化识别收敛性判定条件,确定剖分精度,算例中剖分单元长度1.5 m,取模拟时间步长 2 s 不发生振荡。 3) 仿真计算模型(程序)可以规划出井巷中的热源的影响范围,适用于井下热害防治的工程设计与计算。以上算法同样适用于非稳定热源,如设备开停以及火灾火源强度的变化属于非稳定热源模型,在非稳定计算过程中,随时间调整热源值,具体实现有待于进一步研究。 [1]王省身,张国枢. 矿井火灾防治[M]. 北京:煤炭工业出版社, 1990. [2]刘铁民. 突发事件应急预案体系概念设计研究[J]. 中国安全生产科学技术, 2011, 7(8): 5-13. LIU Tiemin. Design of the emergency plan system’s concept[J]. Journal of Safety Science and Technology, 2011, 7(8): 5-13. [3] 盛伟,郑海坤. 人体降温服在矿井热环境中的应用综述[J]. 中国安全生产科学技术, 2013, 9(12): 95-101 SHENG Wei, ZHENG Hai kun. Literature review on application of body cooled suits in mine thermal environment[J]. Journal of Safety Science and Technology, 2013, 9(12): 95-101. [4]宋远卓,代昌标,陆愈实. 煤矿火灾过程仿真模拟系统的研究[J]. 中国安全生产科学技术, 2006,2(5):55-58. SONG Yuanzhuo, DAI Changbiao, LU Yushi. Research on simulation system for coal mine fire process[J]. Journal of Safety Science and Technology, 2006,2(5):55-58. [5]宋晓燕,谢中朋.三河尖煤矿热力参数测定及热湿源危害分析[J].中国安全生产科学技术,2012,8(12):174-178. SONG Xiaoyan, XIE Zhongpeng. Heat parameter determination of sanhejian mine and research of heat-harm cause[J]. Journal of Safety Science and Technology, 2012,8(12):174-178. [6]李宗翔. 有源风网模型及其应用计算[J]. 煤炭学报, 2010, 35(S1): 118-122. LI Zongxiang. Containing the source ventilation network model and its application[J]. Journal of China Coal Society, 2010, 35(S1): 118-122. [7]王凯,蒋曙光,张卫青,等. 矿井火灾应急救援系统的数值模拟及应用研究[J]. 煤炭学报, 2012, 37(5):857-862 WANG Kai, JIANG Shuguang, ZHANG Weiqing, et al. Numerical simulation and application research of mine fire emergency rescue system[J]. Journal of China Coal Society, 2012, 37(5): 857- 862. [8]贾进章,马恒,刘剑. 矿井火灾时期温度分布数值模拟[J]. 辽宁工程技术大学学报,2003, 22(4): 460-462. JIA Jinzhang,MA Heng,LIU Jian. Numerical simulation for temperature distribution during mine fire period[J]. Journal of Liaoning Technical University,2003,22(4):460-462. [9]丁翠. 火灾时期矿山通风巷道“特征环”与“关键环”的分布特征研究[J]. 中国安全生产科学技术, 2017,13(8):55-60. DING Cui.Study on distribution characteristics of “characteristic ring” and “key ring” in mine ventilation roadway during fire[J]. Journal of Safety Science and Technology,2017,13(8):55-60. [10]张兴凯. 矿井火灾时期风流动态过程的计算[J]. 煤矿安全, 1990, 20(6): 55- 60 ZHANG Xingkai. Mine fire during the dynamic process of calculation[J]. Safety in Coal Mines, 1990, 20(6): 55- 60. [11]戚宜欣. 矿井火灾烟流温度场及浓度场的数值模拟[J]. 西安矿业学院学报, 1994(1):26-33 Qi Yixin. Numerical simulation of temperature and concentration fields of mine fire fume[J]. Journal of Xi’an Mining Institute, 1994(1): 26- 33. [12]李宗翔,王雅迪,李林. 上行风流火灾3D矿井通风系统灾变过程仿真[J]. 煤炭学报, 2015, 40(1): 115-121 LI Zongxiang, WANG Yadi, LI Lin. 3D simulation of disaster process in mine ventilation system during fire period[J]. Journal of China Coal Society, 2015, 40(1): 115-121. [13]章本照. 流体力学中的有限元方法[M]. 北京:机械工业出版社, 1986.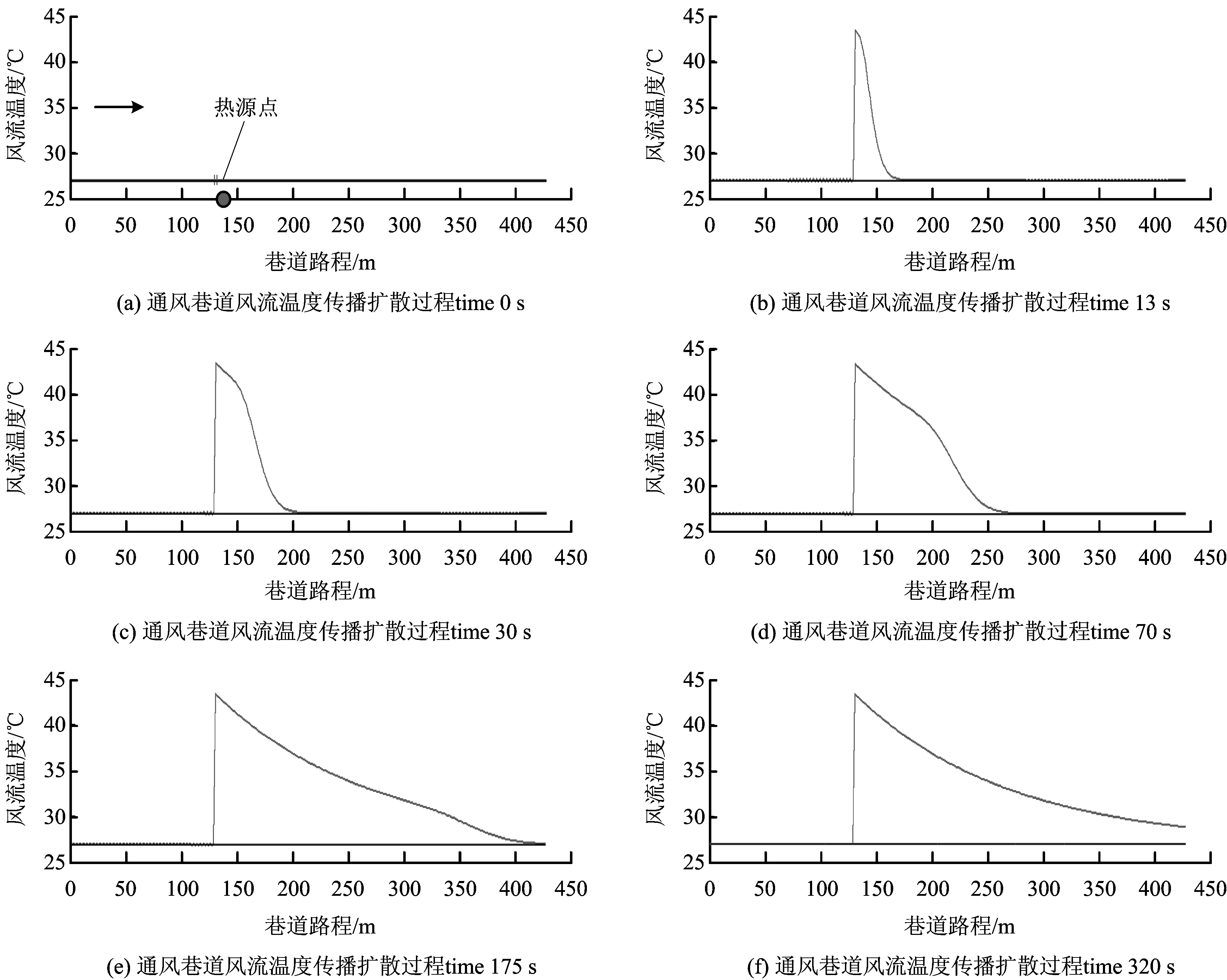
3.3 巷道初始温度分布非恒定的定解条件及求解
3. 4 有限元数值解的收敛性分析
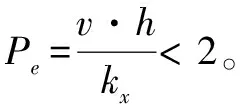
4 结论

